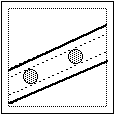
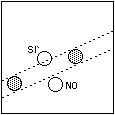
Si lanciano 3 monete uguali su un foglio in cui è tracciato un quadrato di lato pari a 8 volte il diametro delle monete; si considerano soltanto i lanci in cui tutte e tre le monete si fermano completamente dentro al quadrato. Vogliamo scommettere "1 contro N" (N intero) di ottenere con un lancio tre monete allineate, intendendo con ciò che una delle tre monete cada sulla striscia determinata dalle altre due (vedi figura a fianco).
Congettura (senza calcoli) e poi si stima (con un calcolo approssimato o con qualche esperimento) come occorre scegliere N per fare una scommessa conveniente. Come si potrebbe determinare più precisamente la probabilità di ottenere tre monete allineate? [suggerimento: affronta il problema non da solo, ma confrontandoti con qualcun altro]

A prima vista l'evento che le tre monete cadano "allineate" sembra poco probabile. Per N=1 ("1 contro 1") la nostra scommessa sarebbe equa se la probabilità che ci sia allineamento fosse 1/(1+1)=50%; per N=2 ("1 contro 2") sarebbe equa se la probabilità fosse 1/(1+2)=33%; per N=3 ("1 contro 3") sarebbe equa se la probabilità fosse 1/(1+3)=25%; …. Difficilmente si è inclini a pensare, come invece è, che la risposta giusta sia N=2, ma si suppone che la probabilità di allineamento sia molto inferiore al 33%.

Realizzando l'esperimento, dopo pochi lanci è facile convincersi dell'erroneità di queste congetture.
Vediamocome si potrebbe giungere alle stesse conclusioni con una stima "teorica". Fissate due monete, vediamo dove deve cadere il centro della 3^a affinché ci sia "allineamento".
Puòcadere nella striscia determinata dalle due monete (striscia a bordi tratteggiati), allargata da entrambi i lati di un raggio (fino ai bordi spessi), che può essere un parallelogramma - fig.(1) - o un parallelogramma da cui siano stati sforbiciati i pezzi che cadono fuori dal quadrato tratteggiato (entro cui stanno i centri delle monete che fermano interamente dentro al quadrato di lato 20 cm - fig. a lato).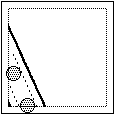

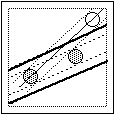
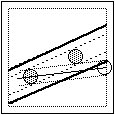
Bisogna aggiungere il caso che una delle monete iniziali stia sulla striscia che la 3^a moneta ha determinato con l'altra moneta iniziale; in fig.(2) e in fig.(3) sono raffigurate le due posizioni limite della 3^a moneta affinché la striscia che essa determina con la moneta più a sinistra tocchi l'altra moneta iniziale.

(1)
(2)
(3)
(4)

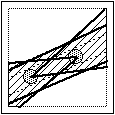
Tracciate le analoghe posizioni limite relative alla striscia che la 3^a moneta può determinare con la moneta più a destra, si ottiene - vedi fig.(4) - la parte di quadrato in cui deve cadere il centro della 3^a moneta affinché ci sia allineamento.

Possiamo stimare che l'area in cui deve cadere il centro della 3^a moneta sia mediamente compresa tra 1/2 e 1/3 dell'area del quadrato in cui può cadere. Quindi per N=2 la nostra scommessa è già conveniente. Ecco 15 prove, dove con "1" si è indicato l'"allineamento", con "0" il non "allineamento" (consideriamo anche il caso, che può accadere, in cui le monete si sovrappongano).

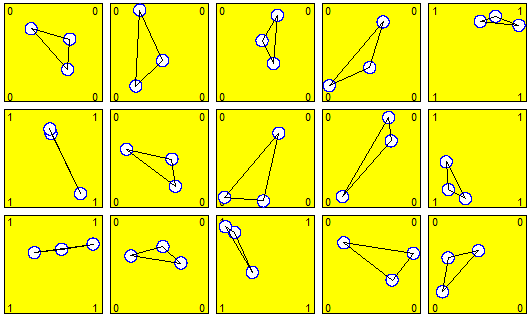
All'origine delle congetture sbagliate con cui, spesso, si affrontano problemi come il seguente vi possono essere il non tener conto degli aspetti combinatori (ci sono 3 modi di fissare la coppia di monete che determina la striscia) e la non abitudine a fare (in contesti scolastici) ragionamenti probabilistici di tipo continuo: qui abbiamo a che fare con rapporti tra aree invece che con rapporti tra numeri.

Per realizzare più facilmente e velocemente gli esperimenti si può ricorrere ad una simulazione. Realizziamola impiegando un programmino in JavaScript, software che è incorporato in tutti i browser. Basta andare qui: http://macosa.dima.unige.it/js/js.htm (puoi vedere anche qui), cliccare "macosa.dima.unige.it/js.com" e mettere nella finestra in alto (lato del quadrato = 8, diametro della moneta = 1, L = Lato del quadrato in cui deve cadere il centro della moneta = 7, dis = distanza di una moneta dalla retta passante per le altre 2):

<pre><script> with(Math) {
lato=8; diam=1; L=lato-diam; X=new Array(3); Y=new Array(3)
n=1e4; x=0; for(M=0; M<n; M=M+1)
{ for(i=1;i<=3;i=i+1) {X[i]=random()*L+1/2; Y[i]=random()*L+1/2}; s=0
  for(i=1;i<=3;i=i+1) {j=i+1; if(j==4) j=1; k=j+1; if(k==4) k=1
       aa=(Y[j]-Y[k])/(X[j]-X[k]); kk=-X[j]*aa+Y[j]
       dis=abs(aa*X[i]-Y[i]+kk)/sqrt(aa*aa+1); if(dis<diam) {s=1;i=4}; x=x+s}
}
document.writeln ("n=",n,"  fr = ", x/n*100,"%")
n=n*10; x=0; for(M=0; M<n; M=M+1)
{ for(i=1;i<=3;i=i+1) {X[i]=random()*L+1/2; Y[i]=random()*L+1/2}; s=0
  for(i=1;i<=3;i=i+1) {j=i+1; if(j==4) j=1; k=j+1; if(k==4) k=1
       aa=(Y[j]-Y[k])/(X[j]-X[k]); kk=-X[j]*aa+Y[j]
       dis=abs(aa*X[i]-Y[i]+kk)/sqrt(aa*aa+1); if(dis<diam) {s=1;i=4}; x=x+s}
}
document.writeln ("n=",n,"  fr = ", x/n*100,"%")
} </script></pre>

Ottengo:

n=10000  fr = 42.23%
n=100000  fr = 42.118%

Bastano poche migliaia di uscite per convincersi che la probabilità è circa del 42%. Con più uscite si potrebbe dedurre che la probabilità cercata è 42.05%. Per ulteriori commenti Limiti in probabilità ne Gli Oggetti Matematici.

Vediamo come si potrebbe trovare una precisione per i valori via via calcolati sperimentalmente. Impieghiamo un programmino in JavaScript leggermente più complesso. Vedi qui.

<pre><script> with(Math) {
lato=8; diam=1; L=lato-diam; X=new Array(3); Y=new Array(3)
n=1e4; x=0; for(M=0; M<n; M=M+1)
{ for(i=1;i<=3;i=i+1) {X[i]=random()*L+1/2; Y[i]=random()*L+1/2}; s=0
  for(i=1;i<=3;i=i+1) {j=i+1; if(j==4) j=1; k=j+1; if(k==4) k=1
       aa=(Y[j]-Y[k])/(X[j]-X[k]); kk=-X[j]*aa+Y[j]
       dis=abs(aa*X[i]-Y[i]+kk)/sqrt(aa*aa+1); if(dis<diam) {s=1;i=4}; x=x+s}
}
document.writeln("n=",n,"  P = ",x/n*100,"%  +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
n=n*10; x=0; for(M=0; M<n; M=M+1)
{ for(i=1;i<=3;i=i+1) {X[i]=random()*L+1/2; Y[i]=random()*L+1/2}; s=0
  for(i=1;i<=3;i=i+1) {j=i+1; if(j==4) j=1; k=j+1; if(k==4) k=1
       aa=(Y[j]-Y[k])/(X[j]-X[k]); kk=-X[j]*aa+Y[j]
       dis=abs(aa*X[i]-Y[i]+kk)/sqrt(aa*aa+1); if(dis<diam) {s=1;i=4}; x=x+s}
}
document.writeln("n=",n,"  P = ",x/n*100,"%  +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
} </script></pre>

Ottengo (anche per n=1e6 e n=1e7 - si potrebbe proseguire con n maggiori, avendo tempo per attendere le uscite ...):

n=10000  P = 41.84%  +/- 0.8544359683170057%
n=100000  P = 41.92%  +/- 0.480602088718276%
n=1000000  P = 42.06%  +/- 0.27038625807236105%
n=10000000  P = 42.06601%  +/- 0.15205230867322742%

Si potrebbe anche questo script modificando TruthValue nel modo seguente.

function TruthValue() { with(Math) { Lato = 8; Diam = 1; L = Lato-Diam x = new Array(3); y = new Array(3); for(i=1; i<=3; i++) { x[i] = random()*L+1/2; y[i] = random()*L+1/2 } V=0; for(i=1; i<=3; i++) { j=i+1; if(j==4) {j=1}; k=j+1; if(k==4) {k=1} aa = Number(y[j]-y[k]) / Number(x[j]-x[k]); kk=Number( -x[j]*aa+y[j] ); dis = abs( Number(aa*x[i]-y[i])+kk)/sqrt( Number(aa*aa+1) ); if(dis < Diam) {V=1; i=4} } }} n=10240000 42.05263671875% +/- 0.04627908385971092% n=5120000 42.06546875% +/- 0.06545124797149059% n=2560000 42.084296875% +/- 0.09256771880357534% n=1280000 42.08421875% +/- 0.13091051572299797% n=640000 42.07078125% +/- 0.18512741255302856% n=320000 42.083125% +/- 0.26182040816437696% n=160000 42.03625% +/- 0.37021400257017895% n=80000 42.0575% +/- 0.5235996132578906% n=40000 41.995% +/- 0.7403348544864136% n=20000 41.995% +/- 1.0470046798796957% n=10000 41.76% +/- 1.479564486971457%

Ecco la simulazione realizzata con R (vedi qui), con cui è stato ottenuto il grafico precedente.

source("http://macosa.dima.unige.it/r.R") SUC <- function(i) ifelse(i==3,1,i+1) Event = function() { V = 0; x = NULL; y = NULL; Lato = 8; Diam = 1; L = Lato-Diam for(i in 1:3) { x[i] = runif(1)*L+1/2; y[i] = runif(1)*L+1/2 }; i=1 while(i<=3) { j=SUC(i); k=SUC(j); d=point_line(x[i],y[i], x[j],y[j],x[k],y[k]); i=i+1; if(d < Diam) {V = 1; i = 4} }; x <<- x; y <<- y; V } genera = function() { polyC(c(0,8,8,0),c(0,0,8,8),"yellow") n = ifelse(Event(),1,0) text(0.5,0.5,n); text(7.5,7.5,n); text(0.5,7.5,n); text(7.5,0.5,n) for(i in 1:3) {circleC(x[i],y[i], 1/2, "white");circl(x[i],y[i], 1/2, "blue")} polyC(x,y, 0); } rowcol(3,5); for(i in 1:15) {BoxmW(0,8, 0,8); genera()}