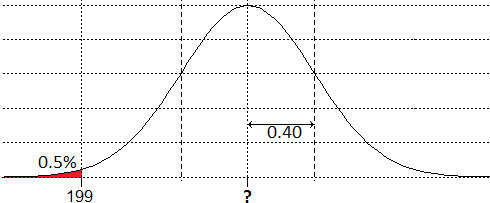
Delle bottiglie contenenti un liquido particolare sono riempite e tappate con un processo automatico. Le bottiglie devono contenere 200 cm³ di liquido ed è ammesso un errore di 1.00 cm³. L'esame di un grande numero di bottiglie rivela che il liquido immesso ha una distribuzione normale con deviazione standard di 0.40 cm³. Se il valor medio del liquido introdotto può essere variato, quale deve essere il suo valore affinché solo lo 0.5% delle bottiglie contenga meno di 199.00 cm³? [usa del software per svolgere i calcoli]
Una rappresentazione grafica ci consente di capire meglio il problema e può indirizzarci a come risolverlo (potremo realizzarla anche online con WolframAlpha):

Disponendo di un computer o di un cellulare il modo più semplice per risolverlo consiste nel procedere per approssimazioni successive. Vediamo come con lo script gauss:
0.5 if a=-inf b=199, m=199 sigma=0.4 0.0062096653258 if a=-inf b=199, m=200 sigma=0.4 0.0029797632351 if a=-inf b=199, m=200.1 sigma=0.4 0.004332448363 if a=-inf b=199, m=200.05 sigma=0.4 0.0050120043318 if a=-inf b=199, m=200.03 sigma=0.4 ... 0.0049999971594 if a=-inf b=199, m=200.0303318 sigma=0.4 0.0050000007743 if a=-inf b=199, m=200.0303317 sigma=0.4 |
Concludo che il valor medio (arrotondato ai centesimi) è 200.03 o (ai milionesimi, ma è un valore senza alcun senso) 200.030332.
# Facciamo i calcoli anche con R. # Una generica gaussiana: f <- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2)) # So che: s <- 0.4 # Provo col valore iniziale: m <- 200; integrate(f,-Inf,199) # 0.006209666 with absolute error < 9.5e-07 # Devo provare con un valore maggiore: m <- 200.1; integrate(f,-Inf,199) # 0.002979763 with absolute error < 2e-05 # Devo provare con un valore minore: m <- 200.01; integrate(f,-Inf,199) # 0.005784915 with absolute error < 3.3e-06 # Maggiore: m <- 200.02; integrate(f,-Inf,199) # 0.005386146 with absolute error < 5.9e-06 # Maggiore: m <- 200.03; integrate(f,-Inf,199) # 0.005012005 with absolute error < 8.6e-06 # Capisco che va bene, ma controllo che cosa accadrebbe aumentando: m <- 200.04; integrate(f,-Inf,199) # 0.004661188 with absolute error < 1.1e-05 # # Concludo che il valor medio (arrotondato ai centesimi) è 200.03 # # Ovvero posso usare la funzione ripartizione della gaussiana predefinita: t <- function(x) pnorm(x,mean=m,sd=0.40) m <- 200.01; t(199) # 0.005784914 m <- 200.02; t(199) # 0.005386146 m <- 200.03; t(199) # 0.005012004 # Faccio le stesse conclusioni.