Con una complessa apparecchiatura ottengo delle misure (con precisione incerta) del diametro di un particolare oggetto che sappiamo essere sferico ma che non siamo in grado di osservare. Otteniamo, in una opportuna misura di lunghezza, i seguenti 30 valori valori, dove in rep(X,N) X indica il valore e N la sua frequenza:
rep(1,1), rep(2,1), rep(3,3), rep(4,4), rep(5,6)
rep(6,5), rep(7,4), rep(8,3), rep(9,2), rep(10,1)
Dall'istogramma abbiamo che la distribuzione dei valori è approssimativamente gaussiana. Verifica questa cosa con dell'opportuno software e, con lo stesso, verifica se la stessa cosa si può dire dei valori della massa della sferetta ottenibili da essi.

• Posso procedere con degli script online. Con questa calcolatrice posso calolare facilnte i cubi. Se metto 1,2,3*3,4*4,5*6,6*5,7*4,8*3,9*2,10 nel box lungo, metto 3 in Q e clicco [data^Q] ottengo 1,8,27*3,64*4,125*6,216*5,343*4,512*3,729*2,1000. Con [copy] posso copiare l'essito nel box lungo. Posso usare la calcolatrice anche per alcune elaborazioni statistiche. Ma usiamo direttamente un altro script.

Con lo script histogram ottengo:

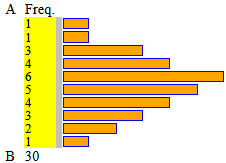A = 0.5 B = 10.5 intervals = 10 their width = 1
min=1 max=10 median=5 1^|3^ quartile= 4|7 mean=5.6
1,2,3*3,4*4,5*6,6*5,7*4,8*3,9*2,10
%: | 3.33 | 3.33 | 10 | 13.33 | 20 | 16.67 | 13.33 | 10 | 6.67 | 3.33 |

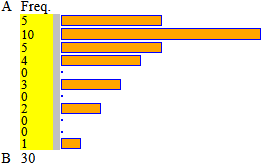A = -50 B = 1050 intervals = 11 their width = 100
min=1 max=1000 median=125 1^|3^ quartile= 64|343 mean=251.4
1, 8, 27*3, 64*4, 125*6, 216*5, 343*4, 512*3, 729*2, 1000
%: | 16.67 | 33.33 | 16.67 | 13.33 | 0 | 10 | 0 | 6.67 | 0 | 3.33 |

I diametri delle sferette hanno andamento "gaussiano", ma i loro cubi (e i valori che siano ottenuti da essi mediante una funzione non lineare) non hanno andamento gaussiano. Quanto ottenuto con questi script è sufficiente per rispondere al quesito. Sotto vediamo qualche approfondimento.

Per altri commenti: Limiti in probabilità neGli Oggetti Matematici.

• Ecco con R (vedi) l'analisi dei dati; in modo simile avrei potuto procedere con altro software; sotto l'analisi col software online Wolframlpha. Prima osserviamo rapidamente l'esito dello "stem and leaf", poi facciamo gli istogrammi.

source("http://macosa.dima.unige.it/r.R")
dati = c(rep(1,times=1),rep(2,1),rep(3,3),rep(4,4),
    rep(5,6),rep(6,5),rep(7,4),rep(8,3),rep(9,2),rep(10,1) )
stem(dati)
#  The decimal point is at the |
#   1 | 0
#   2 | 0
#   3 | 000
#   4 | 0000
#   5 | 000000
#   6 | 00000
#   7 | 0000
#   8 | 000
#   9 | 00
#  10 | 0
#
stem(dati^3)
#  The decimal point is 2 digit(s) to the right of the |
#   0 | 013336666
#   1 | 333333
#   2 | 22222
#   3 | 4444
#   4 | 
#   5 | 111
#   6 | 
#   7 | 33
#   8 | 
#   9 | 
#  10 | 0
# Dagli stem la situazione è già chiara, comunque facciamo gli istogrammi, sovrapponendo
# la gaussiana.

c(min(dati), max(dati), mean(dati))
#  1.0 10.0  5.6
# faccio l'istogramma in scala automatica; con questo comando devo usare "dev.new"
# se voglio usare una nuova finestra
dev.new(); hist(dati, n=10, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
# visto l'andamento scelgo la finestra:
Plane(-1,12, 0, 0.25)
hist(dati, n=10, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey", add=TRUE)
z = function(x) dnorm(x,mean=mean(dati),sd=sd(dati))
graph(z,-1,12, "red")
#
c(min(dati^3), max(dati^3), mean(dati^3))
#   1.0 1000.0  251.4
dev.new(); hist(dati^3, n=10, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey")
# visto l'andamento scelgo la finestra:
Plane(-1,1000, 0, 0.003)
hist(dati^3, n=10, right=FALSE, probability=TRUE, cex.axis=0.8, col="grey", add=TRUE)
z1 = function(x) dnorm(x,mean=mean(dati^3),sd=sd(dati^3))
graph(z1,-1,1000, "red")

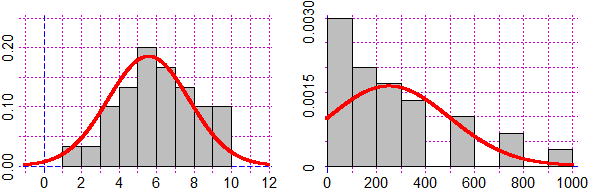
Se dei dati hanno andamento gaussiano, valori che siano ottenuti da questi mediante una funzione non lineare non hanno andamento gaussiano.

• L'analisi col software online WolframAlpha: vedi,

Analizziamo sia i dati che i loro cubi mediante degli "stem and leaf":

(1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10)^3
1,8,27,27,27,64,64,64,64,125,125,125,125,125,125,216,216,216,216,216,343,343,343,343,512,512,512,729,729,1000
stem-and-leaf plot 1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10
stem-and-leaf plot 1,8,27,27,27,64,64,64,64,125,125,125,125,125,125,216,216,216,216,216,343,343,343,343,512,512,512,729,729,1000

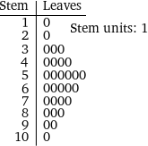
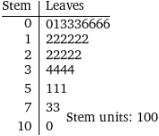
Tieni conto, esaminando il secondo grafico, che se a un valore non corrispondono uscite (come accade per 4, 6, 8 e 9) la riga dello stem non viene scritta.

Dagli stem la situazione è già chiara, comunque facciamo gli istogrammi e confrontiamoli con le gaussiane.
Cotiamo i dati:
len 1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10
30
Facciamo gli istogrammi:
histogram [{1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10},1]
histogram [{1,8,27,27,27,64,64,64,64,125,125,125,125,125,125,216,216,216,216,216,343,343,343,343,512,512,512,729,729,1000},1]

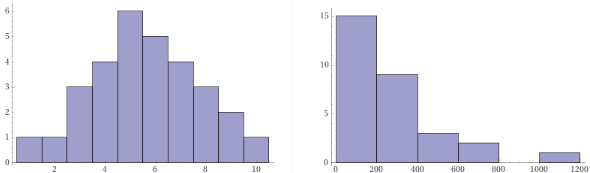
È evidente che il secondo istogramma non è compatibile con una gaussiana.

Comunuque tracciamo anche le gassiane con le stesse medie e deviazioni standard.
mean 1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10
28/5 = 5.6
sd 1,2,3,3,3,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,7,7,7,7,8,8,8,9,9,10
26/sqrt(145) ≈ 2.1592
mean 1,8,27,27,27,64,64,64,64,125,125,125,125,125,125,216,216,216,216,216,343,343,343,343,512,512,512,729,729,1000
1257/5 = 251.4
sd 1,8,27,27,27,64,64,64,64,125,125,125,125,125,125,216,216,216,216,216,343,343,343,343,512,512,512,729,729,1000
sqrt(8847586/145) ≈ 247.02
plot y=exp(-((x-m)/s)^2/2)/(sqrt(2*PI)*s), for s=26/sqrt(145),m=5.6 from x=1 to 10
plot y=exp(-((x-m)/s)^2/2)/(sqrt(2*PI)*s), for s=sqrt(8847586/145),m=251.4 from x=1 to 1000

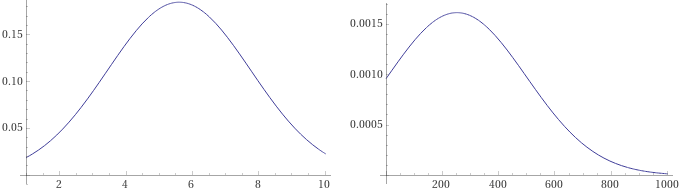
È ulteriormente evidente che l'istogramma dei cubi non aveva andamento "gaussiano".