Misurando la dilatazione lineare di un metallo un ricercatore stima che la deviazione standard sia 0.05 mm. Che dimensione deve avere il campione delle misure per avere la fiducia del 99% che la precisione da associare al valore medio sia inferiore a 0.01 mm?

Supponiamo che la numerosità N del campione sia grande (controllermo questa ipotesi dopo).
La distribuzione delle medie è dunque normale (cioè gaussiana), con deviazione standard sd = 0.05/√N.

Ricordimo (vedi) che, dato un evento E di cui valuto la probabilità studiandone la frequenza, si dice che all'intervallo frequenza ± 3 σ/√n è associata la probabilità di confidenza del 99.7% che esso contenga la probabilità Pr(E) cercata.  Più in generale, si dice che al coefficiente fiduciario t si associa la probabilità di confidenza che l'intervallo frequenza ± t·σ/√n sia veramente un intervallo di indeterminazione per Pr(E);  t viene chiamato coefficiente fiduciario.

Affrontiamo il problema prima con del semplice software online, poi procederemo usando del software statistico.

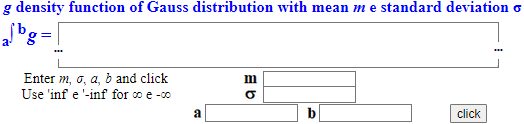
Innanzi tutto devo calcolare il coefficiente fiduciario (cioè il coefficiente di σ) che corrisponde a 99%. Impiego un semplice script per calcolare la densità della gaussiana. Basta che ci riferiamo a quella di media 0 e scarto quadratico medio 1. Calcoliamo per tentativi ragionati h tale che _−h∫^h g = 99%. 

0.95449973539  if a = -2  b = 2,  m=0 sigma=1
0.99067762395  if a = -2.6  b = 2.6,  m=0 sigma=1
0.99000493537  if a = -2.576  b = 2.576,  m=0 sigma=1
0.99000002014  if a = -2.57583  b = 2.57583,  m=0 sigma=1

Prendiamo h = 2.57583 (anche se sarebbe sufficiente prendere 2.576) come coefficiente fiduciario.

A questo punto devo trovare n tale che  h·sd = h·0.05/√n = 0.01, ossia  n = (h·0.05/0.01)² = (5·2.57583)².

Utilizzando ad esempio questa calcolatrice trovo  pow( 2.57583*0.05 / 0.01, 2 ) = 165.87250472...
Devo prendere il primo intero N maggiore di questo valore:  166.
Questa è la dimensione del campione cercata, e abbiamo una conferma che N è sufficientemente grande

Il calcolo del coefficiente fiduciario svolto con l'ausilio di R (vedi):

source("http://macosa.dima.unige.it/r.R")   # If I have not loaded the library
dn = function(x) dnorm(x, mean=0, sd=1 )
idn = function(x) integral(dn,-x,x)
solution(idn,0.99, -100,100)
# 2.575829  il coefficiente fiduciario

Cerco N tale che:

# CoeFid*0.05/sqrt(N) = 0.01; sqrt(N) = CoeFid*0.05/0.01; quindi N e':
(solution(idn,0.99, -100,100)*0.05/0.01)^2
# 165.8724

Per avere N intero devo prendere un maggiorante intero di tale valore:  N = 166.