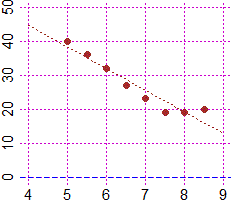
x: 5,5.5,6,6.5,7,7.5,8,8.5 y: 40,36,32,27,23,19,19,20
y = -6.380952380952381 * x + 70.07142857142858
correl. coeff.: -0.9557784332743721
In un esperimento sulla crescita del grano durante l'inverno si registrano la temperatura media
(in °C) del suolo ad una profondità di 8 cm e i giorni necessari per la germogliazione.
Qual è la correlazione tra temperatura del suolo e tempo necessario per la germogliazione?
T = c(5,5.5,6,6.5,7,7.5,8,8.5)
g = c(40,36,32,27,23,19,19,20)

Con questo script ottengo le uscite precedenti. Il grafico a lato è stato ottenuto con questo script, in cui oltre ai punti ho rappresentato la retta di regressione. Come coefficiente di correlazione ho ottenuto −0.96: c'è, nell'intervallo di temperature considerato, una forte proporzionalità (negativa) tra le due variabili. Il coefficiente di correlazione è abbastanza vicino ad 1. E i punti non sono pochi e appaiono abbastanza allineati. Ma il coefficiente di correlazione non tiene conto della quantità dei dati (se i punti sono pochi è più facile trovare una retta che passi vicino ad essi). Per avere certezza della forte correlazione tra le due variabili posso procedere utilizzando il software online WolframAlpha. Vediamo come. |
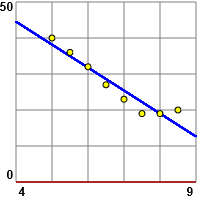 |
Se introduco:
Ottengo: result -0.955778
The null hypothesis that the populations are independent is rejected at the 5 percent level based on the Pearson Correlation test.
p-value 0.000209086
Che cos'è "p-value"? È la probabilità di ottenere, con una data quantità di dati (8 nel nostro caso), il coefficiente di correlazione (-0.955778) nell'ipotesi che le due variabili fossero totalmente scorrelate (ossia che il coefficiente di correlazione fosse effettivamente 0).
Ottengo 0.0209%: c'è una probabilità bassa che i dati siano scorrelati.
Spesso si assume come soglia convenzionale per la possibile esistenza di una correlazione un p-value non superiore al 5%. Per approfondimenti vedi.
Per altri commenti:  correlazione tra var. casuali.
correlazione tra var. casuali.
Con R posso ottenere:
cor.test(T,g, conf.level = 0.95) 95 percent confidence interval: -0.9921962 -0.7691091
L'intervallo di confidenza al 95% è l'intervallo in cui, con la probabilità del 95%, cade il valore esatto del coefficiente di correlazione.
Sotto la rappresentazione grafica dei punti (e il tratteggio della retta di regressione).