Nello studio di un fenomeno fotoelettrico si vuole sperimentare se la
relazione tra due grandezze fisiche k e f è di tipo lineare,
ossia del tipo f = A·k + B, con A e B costanti. Si ottengono, con misurazioni ad alta
sensibilità, i valori seguenti:
K = c( 25, 32, 42, 58, 61); F = c(129,131,180,167,195)
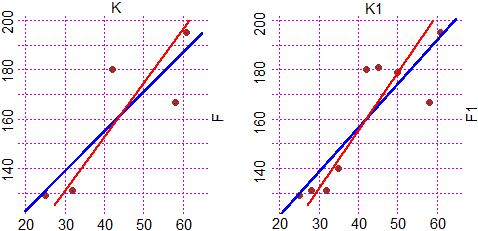
Si ottiene il coefficiente di correlazione 0.856, molto vicino ad 1, e si tracciano
le rette di regressione sia considerando f in funzione di k che viceversa,
ottenendo il grafico sotto a sinistra. Aggiungendo altri rilevamenti
si ottengono i valori seguenti:
K1 = c( 25, 28, 32, 35, 42, 45, 50, 58, 61); F1 =
ottenendo il coefficiente di correlazione 0.871 e il grafico sotto a destra.
| Aver effettuato altri esperimenti è stato utile per ipotizzare l'esistenza di una relazione lineare tra k e f? |  |
Apparentemente la situazione non è molto migliorata. Ma, intuitivamente,
il fatto di aver operato su più dati dovrebbe darci una maggiore sicurezza. Del resto
se avessi avuto solo gli esiti di una coppia di esperimenti, ad esempio
K2 =
Il fatto è che il coefficiente di correlazione (vedi)
determinato su un campione (nel nostro caso le misure ad alta sensibilità effettuate)
non ha un valore "esatto", ma un intervallo di indeterminazione la cui ampiezza dipende anche
dalla quantità dei dati a disposizione. Al di là del modo in cui determinare
l'intervallo di indeterminazione, questo è un aspetto importante da tener presente. Per precisare queste considerazioni
possimamo procedere in due modi.
• Il primo modo, molto semplice, è la determinazione del p-value. Vediamo come farlo e vediamo che cos'è. Non è molto complesso determinarlo "a mano", ma possiamo molto più facilmente usare del software online. Si può farlo su Internet ma impieghiamo del software sicuramente affidabile: WolframAlpha:
Che cos'è "p-value"? È la probabilità di ottenere, con una data quantità di dati, il coefficiente di correlazione nell'ipotesi che le due variabili fossero totalmente scorrelate (ossia che il coefficiente di correlazione fosse effettivamente 0). In genere si assume come soglia convenzionale per la possibile esistenza di una correlazione un p-value non superiore al 5%.
Ottengo in un caso 6.39872%, 0.22212%. nell'altro. Nel primo caso non c'è correlazione tra i dati, come avevamo già intuito. Nel secondo caso il p-value molto basso non contrasta l'esistenza di una correlazione molto forte. Per approfondimenti vedi.
Per trovare le retta facilmente posso impiegare questo script:

|
La retta è f = 1.778·k+84.9. Viene calcolato anche il punto medio (41.8, 159.2), dove nel grafico precedente si incontrano le due rette di regressione (questa e quella di k in funzione di f). Se nel calcolo della regressione scambio x ed y ottengo y = 0.426846963040587 * x - 26.18574422635124, ovvero, per rappresentare la seconda retta di regressione sullo stesso piano della prima, x = A lato la rappresentazione delle due rette con questo script. | 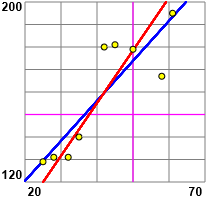 |
• Il secondo modo consiste nel calcolo degli intervalli di indeterminazione, ad es. al 90%. Procediamo (a "scatola nera") con R (vedi) così:
source("http://macosa.dima.unige.it/r.R")
K = c( 25, 32, 42, 58, 61); F = c(129,131,180,167,195)
cor(K,F)
# 0.8562633
K1 = c( 25, 28, 32, 35, 42, 45, 50, 58, 61); F1 = c(129,131,131,140,180,181,179,167,195)
cor(K1,F1)
# 0.8711982
cor.test(K,F, conf.level=0.90)
# 90 percent confidence interval:
# 0.1155630 0.9849879
# sample estimates: cor 0.8562633
cor.test(K1,F1, conf.level=0.90)
# 90 percent confidence interval:
# 0.5826869 0.9646953
# sample estimates: cor 0.8711982
Con 5 dati avevo un intervallo che racchiudeva praticamente tutti i numeri tra 0 ed 1; con 9 dati,
più o meno disposti come i precedenti, ottengo un intervallo da 0.58 a 0.96.
Ecco come sono stati ottenuti i grafici e calcolate e tracciate le rette di regressione:
BF=2.8; HF=2.8; Plane(20,65, 125,200)
POINT(K,F, "brown")
abovex("K"); abovey("F")
regression1(K,F)
# 1.602 * x + 90.57
regression1(F,K)
# 0.4578 * x + -29.82 con x ↔ y
rKF = function(x) 1.602 * x + 90.57
graph2(rKF, 20,65, "blue")
rFK = function(x,y) x - (0.4578 * y + -29.82)
curv(rFK, "red")
#
regression1(K1,F1)
# 1.778 * x + 84.94
regression1(F1,K1)
BF=2.8; HF=2.8; Plane(20,65, 125,200)
POINT(K1,F1, "brown")
graph2(rKF1, 20,65, "blue")
curv(rFK1, "red")
Se penso a f in funzione di k, posso approssimare la relazione con la funzione f = 1.778·k+84.9.