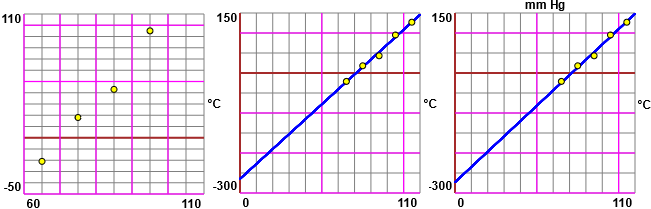
La temperatura varia in funzione di una grandezza fisica G (qui non ci importa quale). Ai valori di G pari a 65, 75, 85, 95 e 105 (arrotondati agli interi, in una opportuna unità di misura), corrispondono i valori delle temperatura (in gradi Celsius) pari, circa, a -21, 18, 43, 95, 127 (rilevati con una la precisione di qualche grado, che non sappiamo quantificare meglio). Ipotizza quale potrebbe essere la funzione.

Affrontiamo il problema con diverse risorse informatiche: con degli script online, con R e con WolframAlpha.

• Rappresentati i dati su un sistema cartesiano con questo script vedo (grafico a sinistra) che sono abbastanza allineati. Calcolo la retta di regressione con questo script (y = 3.73*x - 264.65) e la rappresento allargando la scala con questo script (grafico al centro).
Pare abbastanza chiaro che i dati siano approssimabili con una retta passante per (0, ZeroAssoluto), essendo lo zero assoluto pari a -273.15 °C. Calcolo la retta di regressione vincolata a passare per (0,−273.15) con lo stesso script (trovo y = 3.8273*x - 273.15) e la rappresento con questo script (grafico a destra).
I dati sono riferiti alla pressione (in mm di mercurio) di un campione di "gas ideale" (vedi) il cui volume è mantenuto costante. La costante (3.8273 nel nostro caso) dipende da massa, volume e natura del gas.
Ho riprodotto anche il coefficiente di correlazione (quasi 1) fornito dallo script.

x: 65,75,85,95,105 y: -21,18,43,95,127
y = 3.73*x - 264.65

P: 0, -273.15
y = 3.8273063973063977*x - 273.15
coeff:correl.: 0.9954917181463927

Abbiamo ottenuto T = −273.15+k*P con k = 3.8273 (T: temperatura in °C, P: pressione in mm Hg).

Volendo approfondire, ecco come potrei trovare una valutazione della precisione di "k":

T = -273.15 + k*P, k = (T+273.15)/P. Valori di k corrispondenti ai singoli rilevamenti:
(M + 273.15) / Q con M = -21, 18, 43, 95, 127, Q = 65, 75, 85, 95, 105
Usando questa calcolatrice online ottengo:

(M + 273.15) / Q
(-21 + 273.15) / 65 = 3.879230769230769
(18 + 273.15) / 75 = 3.8819999999999997
(43 + 273.15) / 85 = 3.719411764705882
(95 + 273.15) / 95 = 3.8752631578947367
(127 + 273.15) / 105 = 3.8109523809523806
3.879230769230769, 3.882, 3.719411764705882, 3.8752631578947367, 3.8109523809523806
mean = 3.8333716145567536
sigma = 0.03139438863469641
3*sigma = 0.09418316590408923

T = −273.15 + k·P; k = 3.8273 ± 0.0314 o, in modo approssimativo, k = 3.83 ± 0.03, dove intendiamo sempre non un intervallo "certo", ma col 68% di probabilità; prendendo "±0.095" (3σ) avremmo l'intervallo praticamente "certo" 3.827 ± 0.095.

• Soluzione utilizzando R, vedi.

source("http://macosa.dima.unige.it/r.R")
x = c(65,75,85,95,105); y = c(-21,18,43,95,127)
BF=3; HF=3
Plane(50,100, -30,130); POINT(x,y, "brown"); abovey("°C")
regression1(x,y)
#  3.73 * x + -264.7
f = function(x) 3.73 * x - 264.7
graph1(f, 40,110, "blue")

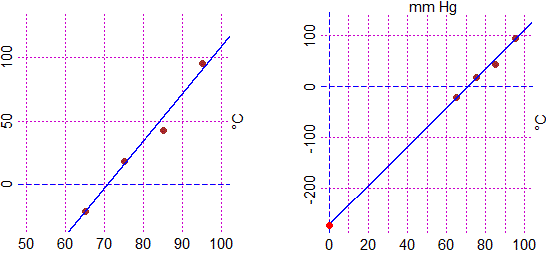
Rappresentati i dati su un sistema cartesiano vediamo che sono abbastanza allineati. Calcoliamo la retta di regressione e rappresentiamola.

Pare abbastanza chiaro che i dati siano approssimabili con una retta passante per (0, ZeroAssoluto), essendo lo zero assoluto pari a -273.15 °C. Calcoliamo la retta di regressione passante per (0,−273.15) - vedi la voce correlazione tra variabili casuali deGli Oggetti Matematici - e rappresentiamola (vedi il grafico soprastante, a destra).

regression(x,y, 0, -273.15)
# 3.827 * (x -  0 ) + -273.15 
T = function(x) 3.827 * x - 273.15
Plane(0,100, -270,130); POINT(x,y, "brown"); abovey("°C")
graph1(T, 0,110, "blue")
POINT(0,-273.15, "red")

I dati sono riferiti alla pressione (in mm di mercurio) di un campione di "gas ideale" (vedi) il cui volume è mantenuto costante. La costante (3.827 nel nostro caso) dipende da massa, volume e natura del gas.
Vediamo quali valori (al posto di -21, 18, 43, 95, 127) otteniamo con la formula:

T(x)
# -24.395  13.875  52.145  90.415 128.685

Abbiamo ottenuto T = −273.15+k*P con k = 3.827. Volendo approfondire, ecco come potrei trovare una valutazione della precisione di "k":

# T = -273.15+k*P, k = (T+273.15)/P
# Valori di k corrispondenti ai singoli rilevamenti
(y+273.15)/x
# 3.879231 3.882000 3.719412 3.875263 3.810952
# Calcolo la deviazione standard della media (vedi):
SdM((y+273.15)/x)
# 0.03139439

T = −273.15 + k·P; k = 3.827 ± 0.032 o, in modo approssimativo, k = 3.83 ± 0.03, dove intendiamo sempre non un intervallo "certo", ma col 68% di probabilità; prendendo "±0.06" (il doppio) avremmo un intervallo col 95% di probabilità.

• Soluzione col software online WolframAlpha, vedi qui.

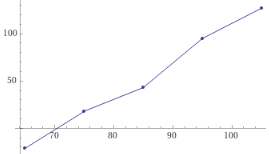
Rappresentati i dati su un sistema cartesiano vediamo che sono abbastanza allineati.
plot (65,-21),(75,18),(85,43),(95,95),(105,127)

Calcoliamo la retta di regressione e rappresentiamola.
linear fit { (65,-21),(75,18),(85,43),(95,95),(105,127)}

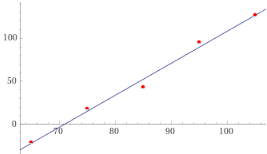
3.73 x - 264.65

-264.65 ≈ -273.15. Pare abbastanza chiaro che i dati siano approssimabili con una retta passante per (0, ZeroAssoluto). Vedi qui come "fissare" un punto, ossia (0,-273.15).
linear fit { (65,-21),(75,18),(85,43),(95,95),(105,127),(0,-273.15),(0,-273.15),(0,-273.15),(0,-273.15),(0,-273.15),(0,-273.15),(0,-273.15)}

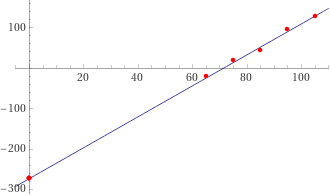
3.82547 x - 272.99 → 3.83*x - 273.15

I dati sono riferiti alla pressione (in mm di mercurio) di un campione di "gas ideale" (vedi) il cui volume è mantenuto costante. La costante (3.83 nel nostro caso) dipende da massa, volume e natura del gas.

Volendo approfondire, ecco come potrei trovare una valutazione della precisione di "k" (vedi):

T = -273.15+k*P, k = (T+273.15)/P. Valori di k corrispondenti ai singoli rilevamenti:
((-21,18,43,95,127)+273.15)/(65,75,85,95,105)
{3.87923, 3.882, 3.71941, 3.87526, 3.81095}

Calcolo la deviazione standard della media:
mean {3.87923, 3.882, 3.71941, 3.87526, 3.81095}
3.83337 sample sd {3.87923, 3.882, 3.71941, 3.87526, 3.81095}
0.0702003
length of {3.87923, 3.882, 3.71941, 3.87526, 3.81095}
5
0.0702003/sqrt(5)
0.0313945...