Sia  :f : x → x^a−1(1−x)^b−1 / ∫ _[0,1] u^a−1(1−u)^b−1 du
Usando opportuni programmi, verifica che, per diversi valori di a e b positivi, f è una funzione densità (tra 0 ed 1) e tracciane il grafico. Verifica che, se a e b sono maggiori di 1, la moda è (a−1) / (a+b−2)  (la distribuzione con tale funzione densità viene chiamata distribuzione beta).

Affrontiamo l'esercizio sia con R che col software online WolframAlpha.

Con R
Vediamo che cosa si ottiene nel caso a = 2 e b = 2 e in altri casi:

source("http://macosa.dima.unige.it/r.R")   # se non già caricato
g = function(u) u^(a-1)*(1-u)^(b-1)
f = function(x) x^(a-1)*(1-x)^(b-1)/integral(g, 0,1)
a = 2; b = 2; integral(f, 0,1)
# 1
plot(f,0,1) # vedi sotto
abline(h=axTicks(2),v=axTicks(1),lty=3)
optimize(f,c(0,1),maximum = TRUE,tol=1e-12)
$maximum  [1] 0.5    $objective  [1] 1.5
(a-1)/(a+b-2)
# 0.5
a = 2; b = 4; integrate(f,0,1)$value
# 1
plot(f,0,1) # vedi sotto
abline(h=axTicks(2),v=axTicks(1),lty=3)
optimize(f,c(0,1),maximum = TRUE,tol=1e-12)
$maximum  [1] 0.25    $objective  [1] 2.109375
(a-1)/(a+b-2)
# 0.25
a = 1; b = 1; integrate(f,0,1)$value
# 1
plot(f,0,1, ylim=c(0,1.5)) # vedi sotto
(a-1)/(a+b-2)
# NaN
a = 1; b = 2; integrate(f,0,1)$value
# 1
plot(f,0,1) # vedi sotto
abline(h=axTicks(2),v=axTicks(1),lty=3)
optimize(f,c(0,1),maximum = TRUE,tol=1e-12)
$maximum  [1] 4.230063e-13    $objective  [1] 2
(a-1)/(a+b-2)
# 0

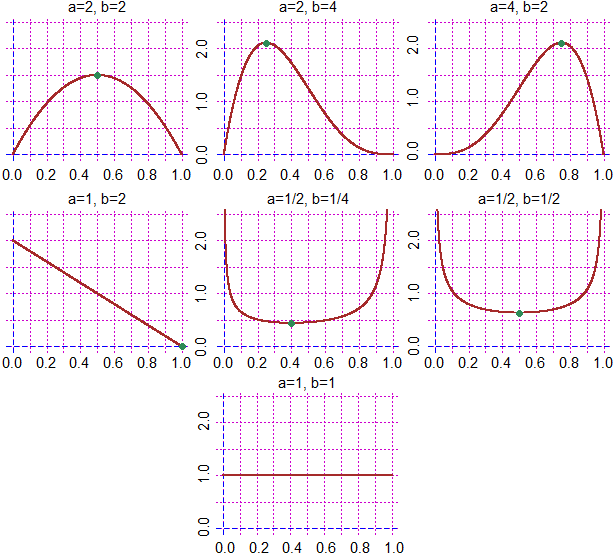
Sopra sono rappresentati anche i grafici che ottengo per altri valori di a e di b. Si tenga presente che se a e b non sono entrambi maggiori di 1 siamo di fronte a integrande non definite in almeno uno dei due estremi di [0,1] (gli integrali che intervengono sono da intendere in senso improprio). R, in questo caso, è comunque in grado di eseguirli. (a-1)/(a+b-2) quando f non è definita in entrambi gli estremi è il punto di minimo.

a = 1/2; b = 1/4; integrate(f,0,1)$value
# 1
plot(f,0,1,ylim=c(0,3),n=1e5)
abline(h=axTicks(2),v=axTicks(1),lty=3)
(a-1)/(a+b-2)
# 0.4
points((a-1)/(a+b-2),f((a-1)/(a+b-2)))
optimize(f,c(0,1),maximum = FALSE,tol=1e-12)
$minimum   [1] 0.4  $objective  [1] 0.4422668

Abbiamo fatto tutti i calcoli con il programma, anche i casi in cui era banale effettuare il calcolo direttamente in forma simbolica. Anche nel caso della moda sarebbe facile verificare direttamente, in modo simbolico, che la derivata prima di f(x), che è ha come fattore x·(a+b−2)−a+1, si azzera per (a-1)/(a+b-2).

Con WolframAlpha
Posso svolgere tutti i calcoli anche online impiegando WolframAlpha:

integrate x^(a-1)*(1-x)^(b-1) dx from 0 to 1 for a=2, b=3
1/12
integrate x^(a-1)*(1-x)^(b-1)/(1/12) dx from 0 to 1 for a=2, b=3
1
plot x^(a-1)*(1-x)^(b-1)/(1/12) from x=0 to 1 for a=2, b=3

(a−1) / (a+b−2) for a=2, b=3
1/3
maximize x^(2  -1)*(1-x)^(3  -1)/(1/12), 0 <= x <= 1
16/9 at x = 1/3