Giovanni si allena. Percorre la stessa strada in salita alla velocità di 11.6 km/h e poi, in discesa, alla velocità di 16.4 km/h.  Qual è stata la sua velocità media?

È sbagliato procedere così:  (11.6+16.4)/2 = 14.0 km/h. Infatti la velocità media non è la media delle velocità, ma è il rapporto tra la lunghezza della strada percorsa e il tempo impiegato. Ecco come devo effettuare il calcolo.
Sia L la lunghezza della strada. In tutto percorro 2L. Da v = s/t ricavo t = s/v. Il tempo (in ore) per la salita è L/11.6, quello per la discesa è L/16.4. In tutto il tempo è L/(1/11.6+1/16.4). Quindi la velocità media è:
      2L/( L/(1/11.6+1/16.4) ) = 2/(1/11.6+1/16.4) = 13.6 km/h.

Volendo usare un termine specifico, possiamo dire che la velocità media è la media armonica delle due velocità (la media armonica è il reciproco della media dei reciproci).  Per altri commenti: valori medi (1) neGli Oggetti Matematici.

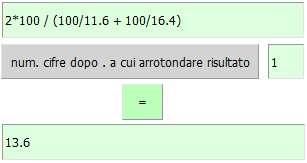
Posso calcolare direttamente la media armonica con la nostra calcolatrice:

harmonic mean = 13.588571428571429

che arrotondo a 13.6.

# Ovvero, con R, dando un valore qualunque alla lunghezza della strada
# (da cui è indipendente il risultato):
# v=L/t  ->  t=L/v
v1=11.6; v2=16.4; L=100
t1=L/v1; t2=L/v2; v = 2*L/(t1+t2)
#  13.58857
round(v,1)
#  13.6
# Ovviamente, facendo prima delle manipolazioni, potevo calcolare, con lo stesso risultato:
v = 2/(1/v1+1/v2); round(v,1)     # o:
v = 2*v1*v2/(v1+v2); round(v,1)

I calcoli col software online WolframAlpha (vedi): basta introdurre round(2/(1/11.6+1/16.4),0.1). Ovvero posso usare lo script "prima calcolatrice": vedi