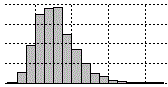
| Qui (per R) o qui (per altro software) puoi recuperare i pesi (troncati ai kg) rilevati ad una visita di leva in Italia del 1987. Analizzalo statisticamente (tracciane l'istogramma, il boxplot, calcola media e mediana, ...). |  |
Prima vediamo come analizzarlo con degli script online. Poi vedremo come si potrebbe impiegare il programma R.
Impieghiamo lo script histogram: apro il file in cui sono presenti i dati, li copio e li incollo nello script. Ottengo,con diverse scelte degli intervalli (e usando anche la versione "tighter rectangles"):
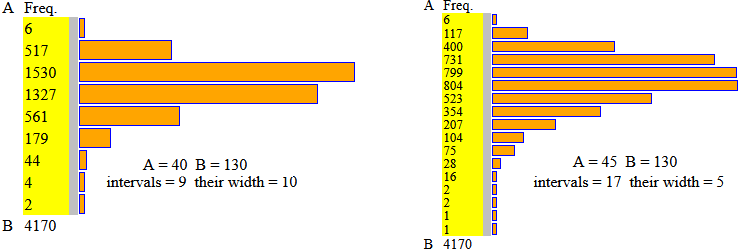
I valori sono troncati. Quindi come media devo prendere, aggiungendo 0.5, 70.97673860911272, o, meglio, 70.98 (kg).
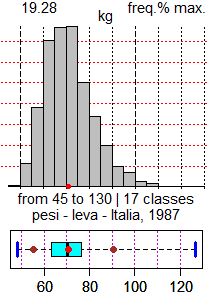
Con lo script box-plot, introdotti gli stessi dati, ottengo:

Viene evidenziata la mediana e 1º e 3º quartile (la parte arancione centrale). Vengono evidenziati anche il 5º e il 95º percentile.
Box-plot, istogramma e la differenza tra le distanze della mediana dal 5º e dal 95º percentile evidenziano che i dati hanno una coda verso destra. A differenza dell'istogramma delle altezze, questo non ha andamento simmetrico. E non può essere altrimenti (perché? prova a rifletterci; più avanti vedrai il perché: prova ad affrontare l'esercizio 5.11).
Puoi salvare il file sul tuo computer o puoi caricarlo direttamente con R.
source("http://macosa.dima.unige.it/r.R")
## Leggo le prime righe del file
readLines("http://macosa.dima.unige.it/om/esr/sta/pesi.txt",n=3)
# [1] "# dati da visite arruolamento in Marina (1997, primi contingenti): peso (troncato ai kg)"
# [2] "62 64 64 68 70"
# [3] "77 65 62 55 60"
## Ho capito come caricare il file (salto la 1^ riga)
pesi = scan("http://macosa.dima.unige.it/om/esr/sta/pesi.txt",skip=1)
# Read 4170 items
str(pesi)
# num [1:4170] 62 64 64 68 70 77 65 62 55 60 ...
## Devo aggiungere 1/2 ai dati, essendo essi troncati!!!
pesi = pesi+1/2
BF=3; HF=2.5
noClass=1; histogram(pesi)
# [the distance of the sides of the grid is 2.5 %]
# Frequencies and percentage freq.:
# 6, 117, 400, 731, 799, 804, 523, 354, 207, 104, 75, 28, 16, 2, 2, 1, 1
# 0.14,2.81,9.59,17.53,19.16,19.28,12.54,8.49,4.96,2.49,1.8,0.67,0.38,0.05,0.05,0.02,0.02
gridVC(seq(0,200,10), 1); GridVC(seq(0,200,50), 1); abovex("kg")
underx2("pesi - leva - Italia, 1987")
Point(mean(pesi),0, "red")
# For other statistics use the command morestat() or statistics(...)
BF=2.6; HF=1.2
statistics(pesi)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 48.50 63.50 70.50 70.98 76.50 126.50
# The brown dots are 5^ and 95^ percentiles
# The red dot is the mean
|
|
 | 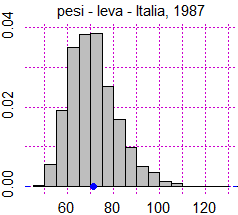 |
# Volendo nella scala verticale le frequenze "unitarie" invece che degli intervalli:
max( hist(pesi, probability=TRUE, plot=FALSE)$density )
# [1] 0.03856115
BF=3; HF=2.5
Plane(45,130, 0, 0.04)
noClass=1; hist(pesi, probability=TRUE, add=TRUE, col="grey")
abovex("pesi - leva - Italia, 1987"); POINT(mean(pesi),0,"blue")
# Ottengo l'istogramma sopra a destra
| |