R. USI GENERALI AVANZATI (altri usi)
Nel programma i comandi
appaiono preceduti da >. Le righe seguenti, scritte in nero (con
eventuali parti in rosso),
possono man mano essere copiate da qui e incollate in R. Il
programma automaticamente le esegue. Le cose scritte in blu sono le uscite
od altri commenti. I grafici, qui riprodotti, in R appaiono in altre finestre.
Rimandiamo a documento "usi di base" per
l'uso dell'help e dei comandi essenziali.
note a capo funz.incorporate e approssimaz. tr.geometriche num.complessi
curve 1 e 2 equaz. polinomiali Re Im tabelle sistemi lineari/matrici
derivate pol.Taylor integrali limiti serie funz.di 2 variab. figure 3D
animaz. a capo bis altro ciclo avviso acust. oper. tra interi codifiche
vettori parab. appr. spline m. mobili prog.lin. mat.fin. altre animaz.
grafi ad albero termini equivalenti scrittura di formule
Indice alfabetico comandi - Indice alfabetico generale attività
# Ricordiamo che tutti i comandi possono essere memorizzati e copiati
# dall'utente quando servono. Che per separare comandi sulla stessa riga
# si usa ";". Che commenti possono essere inseriti preceduti da # e che
# più comandi possono essere raggruppati tra { e }
#
# Ricordiamo, inoltre, che se un comando e' lungo si puo' scriverlo tutto
# su una stessa riga fino a qualche migliaio di caratteri, o si puo'
# andare a capo: la riga successiva viene interpretata come continuazione
#
# Ricordiamo, ancora, che il comando:
rm(list=ls())
# rimuove le precedenti assegnazioni di variabili
#
# Per esaminare altre funzioni incorporate in R si può guardare
# uno dei vari help; ad es. selezionare "R functions (text)", mettere
# "sin" come parola da cercare; si apre "MathFun {base}" e da qui si
# seleziona "Math". Analogamente si può procedere per "pi" (π)
# [al posto di log(x)/log(10) si potrebbe calcolare il log in base 10 usando
# log(x,10) ma si tratta di una funzione che opera correttamente solo in
# alcuni casi]
pi; sin(pi); sin(pi/2); log(exp(7)); log(10^7)/log(10)
[1] 3.141593
[1] 1.224606e-16
[1] 1
[1] 7
[1] 7
gradi <- pi/180; sin(30*gradi); cos(30*gradi); tan(30*gradi); sin(30*gradi)/cos(30*gradi)
[1] 0.5
[1] 0.8660254
[1] 0.5773503
[1] 0.5773503
atan(1); atan(1)/gradi
[1] 0.7853982
[1] 45
# di sin(π/2) per problemi di approssimazione non viene visualizzato
# il valore 0; di π vengono visualizzate solo alcune cifre; possiamo
# esplorarne altre usando, come già visto, print(…,16) o showTree:
print(pi,16); library(codetools); showTree(pi)
[1] 3.141592653589793
3.14159265358979
# i calcoli con variabili sono eseguiti solo se ad esse sono stati assegnati valori
2+a/a
Error: object 'a' not found
a=5; 2+a/a
[1] 3
#
# Usando fractions si possono anche fare calcoli esatti non solo
# con frazioni di interi. Qualche esempio:
library(MASS)
fractions( 2.59807621135332/sqrt(3) )
[1] 3/2
# Deduco che 2.59807621135332 = 3√3/2
fractions( 2.094395102393195/pi )
[1] 2/3
# Deduco che 2.094395102393195 = 2/3*π (potrei usare anche www.wolframalpha.com)
fractions( 4.328085122666891*log(2) )
[1] 3
# Deduco che 4.328085122666891 = 3/log(2)
#
# Vedi qui per la realizzazione di semplici trasformaz. geometriche (vedi anche)
 #
# il programma opera anche sui numeri complessi se compare una "i"
3+sqrt(0.25)
[1] 3.5
3+sqrt(-0.25)
[1] NaN
Warning message:
In sqrt(-0.25) : NaNs produced
# NAN: not a number
3+sqrt(-0.25+0i)
[1] 3+0.5i
z <- 4+3i; Re(z); Im(z); Conj(z)
[1] 4
[1] 3
[1] 4-3i
Mod(z); Arg(z); sqrt(Re(z)^2+Im(z)^2); atan(Im(z)/Re(z))
[1] 5
[1] 0.6435011
[1] 5
[1] 0.6435011
# Vedi qui per come rappresentare graficamente trasformazioni conformi (vedi)
#
# il programma opera anche sui numeri complessi se compare una "i"
3+sqrt(0.25)
[1] 3.5
3+sqrt(-0.25)
[1] NaN
Warning message:
In sqrt(-0.25) : NaNs produced
# NAN: not a number
3+sqrt(-0.25+0i)
[1] 3+0.5i
z <- 4+3i; Re(z); Im(z); Conj(z)
[1] 4
[1] 3
[1] 4-3i
Mod(z); Arg(z); sqrt(Re(z)^2+Im(z)^2); atan(Im(z)/Re(z))
[1] 5
[1] 0.6435011
[1] 5
[1] 0.6435011
# Vedi qui per come rappresentare graficamente trasformazioni conformi (vedi)
 #
# ricordiamo come tracciare curve descritte in forma parametrica:
x1 <- -4; x2 <- 4; y1 <- -4; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="", asp=1)
for(i in (-8:8)/2) abline(h=i,col="grey")
for(i in (-8:8)/2) abline(v=i,col="grey")
abline(h=0,col="brown"); abline(v=0,col="brown")
t1 <- 0; t2 <- 2*pi; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(2*cos(t)+1,3*sin(t)-1, col="blue")
lines(cos(t)+1,3/2*sin(t)-1, col="green")
t1 <- -4; t2 <- 4; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2,t, col="red")
#
# ricordiamo come tracciare curve descritte in forma parametrica:
x1 <- -4; x2 <- 4; y1 <- -4; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="", asp=1)
for(i in (-8:8)/2) abline(h=i,col="grey")
for(i in (-8:8)/2) abline(v=i,col="grey")
abline(h=0,col="brown"); abline(v=0,col="brown")
t1 <- 0; t2 <- 2*pi; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(2*cos(t)+1,3*sin(t)-1, col="blue")
lines(cos(t)+1,3/2*sin(t)-1, col="green")
t1 <- -4; t2 <- 4; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2,t, col="red")
 # Un cerchio e un poligono regolare:
plot(c(-5,7),c(-7,5),type="n",asp=1)
# Togliendo asp=1 posso avere una scala non monometrica
abline(h=axTicks(2),v=axTicks(1),lty=3)
# raggio e centro
r <- 5; C <- c(2,-1); points(C[1],C[2])
t <- seq(0,2*pi,len=5); lines(C[1]+r*cos(t),C[2]+r*sin(t),col="red")
t <- seq(0,2*pi,len=500); lines(C[1]+r*cos(t),C[2]+r*sin(t))
# Un cerchio e un poligono regolare:
plot(c(-5,7),c(-7,5),type="n",asp=1)
# Togliendo asp=1 posso avere una scala non monometrica
abline(h=axTicks(2),v=axTicks(1),lty=3)
# raggio e centro
r <- 5; C <- c(2,-1); points(C[1],C[2])
t <- seq(0,2*pi,len=5); lines(C[1]+r*cos(t),C[2]+r*sin(t),col="red")
t <- seq(0,2*pi,len=500); lines(C[1]+r*cos(t),C[2]+r*sin(t))
 #
# vedi qui per il tracciamento di curve in coordinate polari
#
# vedi qui per il tracciamento di curve in coordinate polari
 #
# Qui come tracciare curve descritte mediante equazioni
#
# Qui come tracciare curve descritte mediante equazioni

 # Qui come risolvere risp. a x o a y equazioni F(x,k) = 0, F(k,y) = 0
#
# Vedi qui per un modo in cui realizzare intersezioni di figure (a sinistra)
# e qui per un altro (a destra). Analogamente posso fare unioni.
# Qui come risolvere risp. a x o a y equazioni F(x,k) = 0, F(k,y) = 0
#
# Vedi qui per un modo in cui realizzare intersezioni di figure (a sinistra)
# e qui per un altro (a destra). Analogamente posso fare unioni.


 #
# in usi di base abbiamo visto come affrontare la risoluzione numerica di
# una qualunque equazione; per le eq. polinomiali possiamo riccorrere a
# polyroot(c(A0,A1,..,An)), dando in input i coefficienti, ordinati (quello
# di grado 0, poi quello di grado 1, quello di grado 2, ...), dei polinomi;
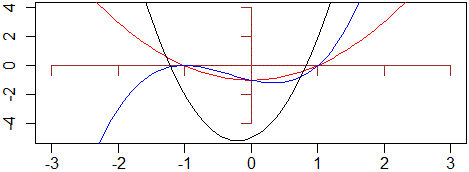
# ad es. per risolvere x^2-1=0, x^3+x^2-x-1=0, 5x^2+2x-5=0 facciamo:
polyroot(c(-1,0,1)); polyroot(c(-1,-1,1,1)); polyroot(c(-5,2,5))
[1] 1+0i -1+0i
[1] 1-0i -1-0i -1+0i
[1] 0.8198039-0i -1.2198039+0i
# le soluzioni sono 1, -1; 1, -1 (-1 punto di tangenza); e
# 0.8198039, -1.2198039; facciamo un controllo grafico:
x1 <- -3; x2 <- 3; y1 <- -5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red");curve(g,add=TRUE,col="blue");curve(h,add=TRUE)
#
# in usi di base abbiamo visto come affrontare la risoluzione numerica di
# una qualunque equazione; per le eq. polinomiali possiamo riccorrere a
# polyroot(c(A0,A1,..,An)), dando in input i coefficienti, ordinati (quello
# di grado 0, poi quello di grado 1, quello di grado 2, ...), dei polinomi;
# ad es. per risolvere x^2-1=0, x^3+x^2-x-1=0, 5x^2+2x-5=0 facciamo:
polyroot(c(-1,0,1)); polyroot(c(-1,-1,1,1)); polyroot(c(-5,2,5))
[1] 1+0i -1+0i
[1] 1-0i -1-0i -1+0i
[1] 0.8198039-0i -1.2198039+0i
# le soluzioni sono 1, -1; 1, -1 (-1 punto di tangenza); e
# 0.8198039, -1.2198039; facciamo un controllo grafico:
x1 <- -3; x2 <- 3; y1 <- -5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red");curve(g,add=TRUE,col="blue");curve(h,add=TRUE)
 # (Otterrei gli stessi risultati mettendo ad es. x^3+x^2-x-1 in WolframAlpha.com)
# Ecco un altro esempio: la soluzione di x^3+3*x+1 = 0
pol <- function(x) 1+3*x+x^3
plot(pol,-3,3); abline(h=0,col="brown"); abline(v=0,col="brown")
# (Otterrei gli stessi risultati mettendo ad es. x^3+x^2-x-1 in WolframAlpha.com)
# Ecco un altro esempio: la soluzione di x^3+3*x+1 = 0
pol <- function(x) 1+3*x+x^3
plot(pol,-3,3); abline(h=0,col="brown"); abline(v=0,col="brown")
 # si capisce che la soluzione è circa -3
polyroot(c(1,3,0,1))
[1] -0.3221854-0.000000i 0.1610927+1.754381i 0.1610927-1.754381i
# per memorizzare questi dati in variabili e/o esaminarne più cifre
# possiamo estrarre le parti reali e immaginarie con Re ed Im;
# vediamo come studiare la prima delle tre soluzioni
polyroot(c(1,3,0,1))[1]
[1] -0.3221854-0i
Re(polyroot(c(1,3,0,1))[1])
[1] -0.3221854
Re(polyroot(c(1,3,0,1))[1])+0.322185
[1] -3.546261e-07
Re(polyroot(c(1,3,0,1))[1])+0.32218535462
[1] -6.087575e-12
Re(polyroot(c(1,3,0,1))[1])+0.32218535462608757
[1] 0
# Questa soluzione (che è reale) avremmo potuto trovarla
# anche con i metodi discussi qui
#
# Una tabella: i valori per le durate di 5, 10, 15, …, 50 anni della
# crescita di 100 € secondo i tassi annuali di interesse composto,
# capitalizzato mensilmente, pari al 6%, all'8%, al 10% e al 12%.
# array indica una variabile indiciata (qui di 11 righe, 4 colonne)
# (una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2)
i <- c(6,8,10,12)/12/100
t <- array(dim=c(11,6)); k <- 0
for (a in seq(0,50,5)) { k <- k+1;
m <- a*12; t[k,1:6] <- c(a,m,round(100*(1+i)^m,2))}
t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 0 100.00 100.00 100.00 100.00
[2,] 5 60 134.89 148.98 164.53 181.67
[3,] 10 120 181.94 221.96 270.70 330.04
[4,] 15 180 245.41 330.69 445.39 599.58
[5,] 20 240 331.02 492.68 732.81 1089.26
[6,] 25 300 446.50 734.02 1205.69 1978.85
[7,] 30 360 602.26 1093.57 1983.74 3594.96
[8,] 35 420 812.36 1629.25 3263.87 6530.96
[9,] 40 480 1095.75 2427.34 5370.07 11864.77
[10,] 45 540 1478.00 3616.36 8835.42 21554.69
[11,] 50 600 1993.60 5387.82 14536.99 39158.34
#
# i sistemi lineari possono essere risolti rappresentandoli
# in forma matriciale. Ad es. x+3y=3 AND 2x+4y=7 lo rappresento con
# le matrici seguenti (gli elementi li introduco colonna per colonna):
ma <- matrix(data = c(1,2,3,4), nrow = 2, ncol = 2)
# Volendo introdurli riga per riga faccio:
ma <- matrix(data = c(1,3,2,4), nrow = 2, ncol = 2, byrow=TRUE)
# [una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2;
# usando array avrei dovuto scrivere:
# ma <- array(data = c(1,2,3,4), dim=c(2,2)) ]
ma
[,1] [,2]
[1,] 1 3
[2,] 2 4
# volendo la trasposta aziono:
t(ma)
[,1] [,2]
[1,] 1 2
[2,] 3 4
det(ma)
[1] -2
noti <- matrix(data = c(3,7), nrow = 2, ncol = 1)
noti
[,1]
[1,] 3
[2,] 7
solve(ma,noti)
[,1]
[1,] 4.5
[2,] -0.5
# facciamo la verifica:
1*4.5+3*-0.5; 2*4.5+4*-0.5
[1] 3
[1] 7
# ovvero, usando il prodotto tra matrici %*%:
sol <- solve(ma,noti); ma %*% sol
[,1]
[1,] 3
[2,] 7
# Altro esempio (inversa, m.identica)
#
# A righe e colonne (le "dimensioni" di una matrice) si possono dare nomi:
nomi <- list(c("proteine","grassi","glucidi"),c("pane","gamberetti","maionese"))
MA <- matrix(data=c(8,1,55,14,1,3,1,80,3), nrow=3, ncol=3, dimnames=nomi); MA
pane gamberetti maionese
proteine 8 14 1
grassi 1 1 80
glucidi 55 3 3
MA <- MA/100; MA # dalle percentuali ai rapporti:
pane gamberetti maionese
proteine 0.08 0.14 0.01
grassi 0.01 0.01 0.80
glucidi 0.55 0.03 0.03
#
# Qui come trovare risolvendo un sistema il cerchio per 3 punti dati
# si capisce che la soluzione è circa -3
polyroot(c(1,3,0,1))
[1] -0.3221854-0.000000i 0.1610927+1.754381i 0.1610927-1.754381i
# per memorizzare questi dati in variabili e/o esaminarne più cifre
# possiamo estrarre le parti reali e immaginarie con Re ed Im;
# vediamo come studiare la prima delle tre soluzioni
polyroot(c(1,3,0,1))[1]
[1] -0.3221854-0i
Re(polyroot(c(1,3,0,1))[1])
[1] -0.3221854
Re(polyroot(c(1,3,0,1))[1])+0.322185
[1] -3.546261e-07
Re(polyroot(c(1,3,0,1))[1])+0.32218535462
[1] -6.087575e-12
Re(polyroot(c(1,3,0,1))[1])+0.32218535462608757
[1] 0
# Questa soluzione (che è reale) avremmo potuto trovarla
# anche con i metodi discussi qui
#
# Una tabella: i valori per le durate di 5, 10, 15, …, 50 anni della
# crescita di 100 € secondo i tassi annuali di interesse composto,
# capitalizzato mensilmente, pari al 6%, all'8%, al 10% e al 12%.
# array indica una variabile indiciata (qui di 11 righe, 4 colonne)
# (una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2)
i <- c(6,8,10,12)/12/100
t <- array(dim=c(11,6)); k <- 0
for (a in seq(0,50,5)) { k <- k+1;
m <- a*12; t[k,1:6] <- c(a,m,round(100*(1+i)^m,2))}
t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 0 100.00 100.00 100.00 100.00
[2,] 5 60 134.89 148.98 164.53 181.67
[3,] 10 120 181.94 221.96 270.70 330.04
[4,] 15 180 245.41 330.69 445.39 599.58
[5,] 20 240 331.02 492.68 732.81 1089.26
[6,] 25 300 446.50 734.02 1205.69 1978.85
[7,] 30 360 602.26 1093.57 1983.74 3594.96
[8,] 35 420 812.36 1629.25 3263.87 6530.96
[9,] 40 480 1095.75 2427.34 5370.07 11864.77
[10,] 45 540 1478.00 3616.36 8835.42 21554.69
[11,] 50 600 1993.60 5387.82 14536.99 39158.34
#
# i sistemi lineari possono essere risolti rappresentandoli
# in forma matriciale. Ad es. x+3y=3 AND 2x+4y=7 lo rappresento con
# le matrici seguenti (gli elementi li introduco colonna per colonna):
ma <- matrix(data = c(1,2,3,4), nrow = 2, ncol = 2)
# Volendo introdurli riga per riga faccio:
ma <- matrix(data = c(1,3,2,4), nrow = 2, ncol = 2, byrow=TRUE)
# [una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2;
# usando array avrei dovuto scrivere:
# ma <- array(data = c(1,2,3,4), dim=c(2,2)) ]
ma
[,1] [,2]
[1,] 1 3
[2,] 2 4
# volendo la trasposta aziono:
t(ma)
[,1] [,2]
[1,] 1 2
[2,] 3 4
det(ma)
[1] -2
noti <- matrix(data = c(3,7), nrow = 2, ncol = 1)
noti
[,1]
[1,] 3
[2,] 7
solve(ma,noti)
[,1]
[1,] 4.5
[2,] -0.5
# facciamo la verifica:
1*4.5+3*-0.5; 2*4.5+4*-0.5
[1] 3
[1] 7
# ovvero, usando il prodotto tra matrici %*%:
sol <- solve(ma,noti); ma %*% sol
[,1]
[1,] 3
[2,] 7
# Altro esempio (inversa, m.identica)
#
# A righe e colonne (le "dimensioni" di una matrice) si possono dare nomi:
nomi <- list(c("proteine","grassi","glucidi"),c("pane","gamberetti","maionese"))
MA <- matrix(data=c(8,1,55,14,1,3,1,80,3), nrow=3, ncol=3, dimnames=nomi); MA
pane gamberetti maionese
proteine 8 14 1
grassi 1 1 80
glucidi 55 3 3
MA <- MA/100; MA # dalle percentuali ai rapporti:
pane gamberetti maionese
proteine 0.08 0.14 0.01
grassi 0.01 0.01 0.80
glucidi 0.55 0.03 0.03
#
# Qui come trovare risolvendo un sistema il cerchio per 3 punti dati
 # Con %*% posso calcolare anche il prodotto scalare (dot product) tra vettori
c(1,-2,2) %*% c(-4,0,2)
[,1]
[1,] 0
# i due vettori (1,-2,2) e (-4,0,2) sono quindi perpendicolari
# Per avere il prodotto scalare come numero usa drop
# drop( c(1,-2,2) %*% c(-4,0,2) )
[1] 0
# Per il prodotto vettoriale (cross product) posso fare:
prodv <- function(x,y) c(x[2]*y[3]-x[3]*y[2],x[3]*y[1]-x[1]*y[3],x[1]*y[2]-x[2]*y[1])
u <- c(0, 2.5, 1); v <- c(0, 2, 2)
prodv(u,v)
[1] 3 0 0
# Il modulo (distanza da O) di u, v e del vettore prodotto, e il versore di u:
dist <- function(P1,P2) sqrt(sum((P1-P2)^2))
dist(0,u); dist(0,v); dist(0, prodv(u,v) ); u/dist(0,u)
[1] 2.692582
[1] 2.828427
[1] 3
[1] 0.0000000 0.9284767 0.3713907
#
# Si possono calcolare facilmente le derivate di una funzione;
# [nota: R non calcola la derivata di abs(x), occore usare sqrt(x^2);
# vedi qui come derivare funzioni definite a tratti]
# ecco le derivate prima, seconda e terza di
# x -> x^2+x^3+sin(2*x)
D(expression(x^2+x^3+sin(2*x)),"x"); D(D(expression(x^2+x^3+sin(2*x)),"x"),"x")
D(D(D(expression(x^2+x^3+sin(2*x)), "x"),"x"),"x")
2 * x + 3 * x^2 + cos(2*x) * 2
2 + 3 * (2 * x) - sin(2*x) * 2 * 2
3 * 2 - cos(2 * x) * 2 * 2 * 2
# invece di expression si può usare quote
# (questi termini sono semplificabili facilmente a mano. Per
# semplificazioni più complesse posso usare WolframAlpha.com)
# Volendo posso definire la funzione e calcolare così le sue derivate
# (infatti body(f) è il termine con cui è stata definita f):
f <- function(x) x^2+x^3+sin(2*x)
D(body(f),"x"); D(D(body(f),"x"),"x"); D(D(D(body(f),"x"),"x"),"x")
# riottengo le stesse uscite.
# Ecco come definire le funzioni derivata, usando eval, che esprime
# il "valore" di un'espressione (in questo caso il valore che
# assume, al variare di x, un certo termine numerico)
g <- function(x) eval(D(body(f),"x"))
h <- function(x) eval(D(D(body(f),"x"),"x"))
k <- function(x) eval(D(D(D(body(f),"x"),"x"),"x"))
# ovvero: gx <- D(body(f),"x"); g <- function(x) eval(gx); ...
# I grafici della funzione e delle sue derivate:
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue")
curve(h,add=TRUE,col="green"); curve(k,add=TRUE,col="magenta")
# Con %*% posso calcolare anche il prodotto scalare (dot product) tra vettori
c(1,-2,2) %*% c(-4,0,2)
[,1]
[1,] 0
# i due vettori (1,-2,2) e (-4,0,2) sono quindi perpendicolari
# Per avere il prodotto scalare come numero usa drop
# drop( c(1,-2,2) %*% c(-4,0,2) )
[1] 0
# Per il prodotto vettoriale (cross product) posso fare:
prodv <- function(x,y) c(x[2]*y[3]-x[3]*y[2],x[3]*y[1]-x[1]*y[3],x[1]*y[2]-x[2]*y[1])
u <- c(0, 2.5, 1); v <- c(0, 2, 2)
prodv(u,v)
[1] 3 0 0
# Il modulo (distanza da O) di u, v e del vettore prodotto, e il versore di u:
dist <- function(P1,P2) sqrt(sum((P1-P2)^2))
dist(0,u); dist(0,v); dist(0, prodv(u,v) ); u/dist(0,u)
[1] 2.692582
[1] 2.828427
[1] 3
[1] 0.0000000 0.9284767 0.3713907
#
# Si possono calcolare facilmente le derivate di una funzione;
# [nota: R non calcola la derivata di abs(x), occore usare sqrt(x^2);
# vedi qui come derivare funzioni definite a tratti]
# ecco le derivate prima, seconda e terza di
# x -> x^2+x^3+sin(2*x)
D(expression(x^2+x^3+sin(2*x)),"x"); D(D(expression(x^2+x^3+sin(2*x)),"x"),"x")
D(D(D(expression(x^2+x^3+sin(2*x)), "x"),"x"),"x")
2 * x + 3 * x^2 + cos(2*x) * 2
2 + 3 * (2 * x) - sin(2*x) * 2 * 2
3 * 2 - cos(2 * x) * 2 * 2 * 2
# invece di expression si può usare quote
# (questi termini sono semplificabili facilmente a mano. Per
# semplificazioni più complesse posso usare WolframAlpha.com)
# Volendo posso definire la funzione e calcolare così le sue derivate
# (infatti body(f) è il termine con cui è stata definita f):
f <- function(x) x^2+x^3+sin(2*x)
D(body(f),"x"); D(D(body(f),"x"),"x"); D(D(D(body(f),"x"),"x"),"x")
# riottengo le stesse uscite.
# Ecco come definire le funzioni derivata, usando eval, che esprime
# il "valore" di un'espressione (in questo caso il valore che
# assume, al variare di x, un certo termine numerico)
g <- function(x) eval(D(body(f),"x"))
h <- function(x) eval(D(D(body(f),"x"),"x"))
k <- function(x) eval(D(D(D(body(f),"x"),"x"),"x"))
# ovvero: gx <- D(body(f),"x"); g <- function(x) eval(gx); ...
# I grafici della funzione e delle sue derivate:
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue")
curve(h,add=TRUE,col="green"); curve(k,add=TRUE,col="magenta")
 # Potrei rivare lo stesso grafico precedente con:
plot(f,-5,5,ylim=c(-30,30),col="red"); abline(v=0,h=0,col="brown")
plot(g,-5,5,add=TRUE,col="blue"); plot(h,-5,5,add=TRUE,col="green4")
plot(k,-5,5,add=TRUE,col="magenta")
# Ecco qui come ottenere un'animazione che traccia secanti e tangente
# ad una curva
# Potrei rivare lo stesso grafico precedente con:
plot(f,-5,5,ylim=c(-30,30),col="red"); abline(v=0,h=0,col="brown")
plot(g,-5,5,add=TRUE,col="blue"); plot(h,-5,5,add=TRUE,col="green4")
plot(k,-5,5,add=TRUE,col="magenta")
# Ecco qui come ottenere un'animazione che traccia secanti e tangente
# ad una curva
 # Se conosco il concetto di polonomio di Taylor, posso approssimare f con
# una funzione polinomiale. Ecco quella di grado 3 (per g,h,k vedi sopra):
# [ vedi qui per una sintesi ]
p <- function(x) f(0)+g(0)*x+h(0)*x^2/factorial(2)+k(0)*x^3/factorial(3)
# e il suo grafico aggiunto a quello di f
plot(p,-5,5,add=TRUE)
# Se conosco il concetto di polonomio di Taylor, posso approssimare f con
# una funzione polinomiale. Ecco quella di grado 3 (per g,h,k vedi sopra):
# [ vedi qui per una sintesi ]
p <- function(x) f(0)+g(0)*x+h(0)*x^2/factorial(2)+k(0)*x^3/factorial(3)
# e il suo grafico aggiunto a quello di f
plot(p,-5,5,add=TRUE)
 #
# in R .Last.value consente di richiamare l'ultima uscita; ecco
# come si potrebbe usare per calcoli come i precedenti:
fun <- function(x) x^4+x^3; D(body(fun),"x")
4 * x^3 + 3 * x^2
D(.Last.value,"x")
4 * (3 * x^2) + 3 * (2 * x)
D(.Last.value,"x")
4 * (3 * (2 * x)) + 3 * 2
D(.Last.value,"x")
4 * (3 * 2)
D(.Last.value,"x")
[1] 0
#
# Ovviamente, è facile determinare punti di minimo/massimo/flesso
# di funzioni di cui si conosce l'espressione analitica: un esempio;
# una animazione.
#
# in R .Last.value consente di richiamare l'ultima uscita; ecco
# come si potrebbe usare per calcoli come i precedenti:
fun <- function(x) x^4+x^3; D(body(fun),"x")
4 * x^3 + 3 * x^2
D(.Last.value,"x")
4 * (3 * x^2) + 3 * (2 * x)
D(.Last.value,"x")
4 * (3 * (2 * x)) + 3 * 2
D(.Last.value,"x")
4 * (3 * 2)
D(.Last.value,"x")
[1] 0
#
# Ovviamente, è facile determinare punti di minimo/massimo/flesso
# di funzioni di cui si conosce l'espressione analitica: un esempio;
# una animazione.
 # (metodi che non impiegano la derivazione sono illustrati qui)
#
# Come ottenere il grafico di una funzione e quello della sua
# derivata in due finestre diverse:
dev.new(width=4,height=4)
view <- c(-3,3, -1,10); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-1,10,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
f <- function(x) x^2
plot(f,view[1],view[2],add=TRUE,col="blue")
dev.new(width=4,height=4)
view <- c(-3,3, -6,6); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-6,6,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
gx <-D(body(f),"x"); g <- function(x) eval(gx)
plot(g,view[1],view[2],add=TRUE,col="blue")
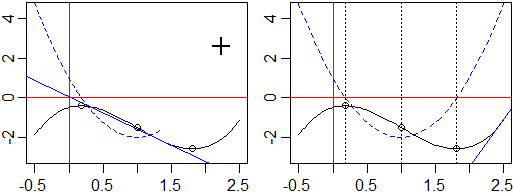
# (metodi che non impiegano la derivazione sono illustrati qui)
#
# Come ottenere il grafico di una funzione e quello della sua
# derivata in due finestre diverse:
dev.new(width=4,height=4)
view <- c(-3,3, -1,10); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-1,10,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
f <- function(x) x^2
plot(f,view[1],view[2],add=TRUE,col="blue")
dev.new(width=4,height=4)
view <- c(-3,3, -6,6); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-6,6,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
gx <-D(body(f),"x"); g <- function(x) eval(gx)
plot(g,view[1],view[2],add=TRUE,col="blue")
 #
# il calcolo di integrali definiti:
t <- function(x) 3*x^2+1; integrate(t,0,1); integrate(t,-1,1)
2 with absolute error < 2.2e-14
4 with absolute error < 4.4e-14
# Se vuoi avere solo il valore aggiungi $value
integrate(t,-1,1)$value
[1] 4
# Ma si possono ottenere facilmente con un programmino: vedi qui o qui
#
# Posso migliorare la precisione relativa del calcolo con rel.tol. Es.:
F <- function(x) sin(x^3)+exp(x)
integrate(F, -5,10)
22027.3 with absolute error < 2.6
integrate(F, -5,10,rel.tol=1e-6)
22026.47 with absolute error < 0.018
print(integrate(F, -5,10,rel.tol=1e-8),16)
22026.46763874626 with absolute error < 6.9e-05
#
# Per il grafico della funzione integrale tra 0 ed x di g posso
# caricare i comandi (area) contenuti nella libreria MASS (ma
# funziona bene solo in casi semplici; per altri casi vedi sotto)
library(MASS)
g <- function(x) 2 * x + 3 * x^2 + cos(x)
k <- function(x) area(g,0,x)
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(g, add=TRUE,col="blue")
curve(k, add=TRUE,col="green")
#
# il calcolo di integrali definiti:
t <- function(x) 3*x^2+1; integrate(t,0,1); integrate(t,-1,1)
2 with absolute error < 2.2e-14
4 with absolute error < 4.4e-14
# Se vuoi avere solo il valore aggiungi $value
integrate(t,-1,1)$value
[1] 4
# Ma si possono ottenere facilmente con un programmino: vedi qui o qui
#
# Posso migliorare la precisione relativa del calcolo con rel.tol. Es.:
F <- function(x) sin(x^3)+exp(x)
integrate(F, -5,10)
22027.3 with absolute error < 2.6
integrate(F, -5,10,rel.tol=1e-6)
22026.47 with absolute error < 0.018
print(integrate(F, -5,10,rel.tol=1e-8),16)
22026.46763874626 with absolute error < 6.9e-05
#
# Per il grafico della funzione integrale tra 0 ed x di g posso
# caricare i comandi (area) contenuti nella libreria MASS (ma
# funziona bene solo in casi semplici; per altri casi vedi sotto)
library(MASS)
g <- function(x) 2 * x + 3 * x^2 + cos(x)
k <- function(x) area(g,0,x)
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(g, add=TRUE,col="blue")
curve(k, add=TRUE,col="green")
 # Usando la funzione "area" è possibile avere direttamente il valore
# di un integrale su un intervallo finito (usa metodi approssimati come
# "integrate" ma non visualizza l'errore):
area(t,0,1); area(t,-1,1)
[1] 2
[1] 4
# Per il graf. della funz. integrale posso anche usare integrate e
# procedere per punti:
a <- -5; b <- 5; x0 <- 0; n <- 5000
for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(g,x0,x)$value,pch=".",col="red") }
#
# Le primitive di una "funzione elementare" non sono sempre funzioni
# elementari, per cui non c'e' modo di avere l'integrale indefinito
# di una qualunque funzione in forma simbolica (in molti casi tuttavia
# posso ricorrere ad es. a WolframAlpha.com). Posso però definire
# definire metodi di calcolo per particolari funzioni. Vediamo come
# farlo per le funzioni polinomiali.
# Mettiamo i coeff. del polinomio a partire dal grado 0
Q <- c(-2,-3,2.4,-1/5) # il pol. -2-3*x+2.4*x^2-1/5*x^3
int <- function(p) { inte <- 0;
for (i in 1:length(p)) inte <- c(inte,p[i]/i); inte}
int(Q)
[1] 0.00 -2.00 -1.50 0.80 -0.05
library(MASS); fractions(int(Q))
[1] 0 -2 -3/2 4/5 -1/20
# Le primitive sono x -> c-2*x-3/2*x^2+4/5*x^3-x^4/20
# Volendo i grafici:
f <- function(x) Q[1]+x*Q[2]+x^2*Q[3]+x^3*Q[4]
plot(f,-3,12,ylim=c(-10,150)); abline(h=0,v=0,lty=3)
g <- function(x) c-2*x-3/2*x^2+4/5*x^3-x^4/20
for(c in (-7:10)*20) plot(g,-3,12,add=TRUE,col="red",lty=3)
# Usando la funzione "area" è possibile avere direttamente il valore
# di un integrale su un intervallo finito (usa metodi approssimati come
# "integrate" ma non visualizza l'errore):
area(t,0,1); area(t,-1,1)
[1] 2
[1] 4
# Per il graf. della funz. integrale posso anche usare integrate e
# procedere per punti:
a <- -5; b <- 5; x0 <- 0; n <- 5000
for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(g,x0,x)$value,pch=".",col="red") }
#
# Le primitive di una "funzione elementare" non sono sempre funzioni
# elementari, per cui non c'e' modo di avere l'integrale indefinito
# di una qualunque funzione in forma simbolica (in molti casi tuttavia
# posso ricorrere ad es. a WolframAlpha.com). Posso però definire
# definire metodi di calcolo per particolari funzioni. Vediamo come
# farlo per le funzioni polinomiali.
# Mettiamo i coeff. del polinomio a partire dal grado 0
Q <- c(-2,-3,2.4,-1/5) # il pol. -2-3*x+2.4*x^2-1/5*x^3
int <- function(p) { inte <- 0;
for (i in 1:length(p)) inte <- c(inte,p[i]/i); inte}
int(Q)
[1] 0.00 -2.00 -1.50 0.80 -0.05
library(MASS); fractions(int(Q))
[1] 0 -2 -3/2 4/5 -1/20
# Le primitive sono x -> c-2*x-3/2*x^2+4/5*x^3-x^4/20
# Volendo i grafici:
f <- function(x) Q[1]+x*Q[2]+x^2*Q[3]+x^3*Q[4]
plot(f,-3,12,ylim=c(-10,150)); abline(h=0,v=0,lty=3)
g <- function(x) c-2*x-3/2*x^2+4/5*x^3-x^4/20
for(c in (-7:10)*20) plot(g,-3,12,add=TRUE,col="red",lty=3)
 # Sono stati evidenziati anche zeri/punti di max/min di f/g:
polyroot(Q)
[1] -0.4772256+0i 2.0000000-0i 10.4772256+0i
abline(v=c(-0.4772256,2.0000000,10.4772256),lty=2,col="blue")
#
# Vedi qui come affrontare, più in generale, lo studio delle
# equazioni differenziali del 1º ordine, e tracciare il campo direzionale.
# Vedi qui per studiare quelle del 2º ordine e tracciarne il diagramma di fase
#
# il simbolo Inf rappresenta l'infinito
# NOTA: come abbiamo visto viene assunto il "valore" Inf quando un numero
# eccede un certo valore. Analogamente viene assunto il valore 0 quando il
# valore assoluto di un numero è molto piccolo. Per dettagli aziona:
.Machine
#
h <- function(x) exp(-x)
x1 <- -1; x2 <- 10; y1 <- -1/10; y2 <- 1
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(h, add=TRUE, col="blue")
# Sono stati evidenziati anche zeri/punti di max/min di f/g:
polyroot(Q)
[1] -0.4772256+0i 2.0000000-0i 10.4772256+0i
abline(v=c(-0.4772256,2.0000000,10.4772256),lty=2,col="blue")
#
# Vedi qui come affrontare, più in generale, lo studio delle
# equazioni differenziali del 1º ordine, e tracciare il campo direzionale.
# Vedi qui per studiare quelle del 2º ordine e tracciarne il diagramma di fase
#
# il simbolo Inf rappresenta l'infinito
# NOTA: come abbiamo visto viene assunto il "valore" Inf quando un numero
# eccede un certo valore. Analogamente viene assunto il valore 0 quando il
# valore assoluto di un numero è molto piccolo. Per dettagli aziona:
.Machine
#
h <- function(x) exp(-x)
x1 <- -1; x2 <- 10; y1 <- -1/10; y2 <- 1
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(h, add=TRUE, col="blue")
 integrate(h,0,Inf)
1 with absolute error < 5.7e-05
# per avere l'uscita numerica senza la precisone basta usare $value:
integrate(h,0,Inf)$value
[1] 1
# il limite per x -> Inf di h è 0:
h(1); h(10); h(100); h(Inf)
[1] 0.3678794
[1] 4.539993e-05
[1] 3.720076e-44
[1] 0
# nota: la funzione "area" è usabile solo per calcolare integrali
# su intervalli finiti: area(h,0,Inf) segnalerebbe "errore"
#
# Attenzione: il limite di f(x) per x -> Inf è stimabile con f(Inf) non in
# tutti i casi. È beve valutare f(x) per x che cresce per controllare. Es.:
f <- function(x) (1+1/x)^x; f(Inf)
[1] 1
# mentre il limite è e:
n <- 1:8; f(10^n)
[1] 2.593742 2.704814 2.716924 2.718146 2.718268 2.718280 2.718282 2.718282
#
# i limiti di q(x) per q che tende ad 1 da destra e da sinistra sono diversi
q <- function(x) (x^2-1)/(x^2-2*x+1); plot(q,-2,2)
integrate(h,0,Inf)
1 with absolute error < 5.7e-05
# per avere l'uscita numerica senza la precisone basta usare $value:
integrate(h,0,Inf)$value
[1] 1
# il limite per x -> Inf di h è 0:
h(1); h(10); h(100); h(Inf)
[1] 0.3678794
[1] 4.539993e-05
[1] 3.720076e-44
[1] 0
# nota: la funzione "area" è usabile solo per calcolare integrali
# su intervalli finiti: area(h,0,Inf) segnalerebbe "errore"
#
# Attenzione: il limite di f(x) per x -> Inf è stimabile con f(Inf) non in
# tutti i casi. È beve valutare f(x) per x che cresce per controllare. Es.:
f <- function(x) (1+1/x)^x; f(Inf)
[1] 1
# mentre il limite è e:
n <- 1:8; f(10^n)
[1] 2.593742 2.704814 2.716924 2.718146 2.718268 2.718280 2.718282 2.718282
#
# i limiti di q(x) per q che tende ad 1 da destra e da sinistra sono diversi
q <- function(x) (x^2-1)/(x^2-2*x+1); plot(q,-2,2)
 q(1-1E-2);q(1-1E-5);q(1-1E-10)
[1] -199
[1] -199999
[1] -Inf
q(1+1E-2);q(1+1E-5);q(1+1E-10)
[1] 201
[1] 200001
[1] Inf
#
# Un altro esempio. Lo studio, data una funzione f, dei punti di flesso
# che assume in [0,5] la sua primitiva F avente valore 0 in 0. Qui i
# valori sono trovati arrotondati ai centesimi (sono tracciate in verde
# scuro le rette verticali che li hanno come ascissa: vedi l'ultimo
# comando "abline").
f <- function(x) x+sin(x)^4*cos(x)^5*60
a <- 0; b <- 5
plot(f,a,b,ylim=c(-7,10)); abline(h=0)
abline(v=c(0,1,2,3,4,5),lty=3,col="grey")
fx <- body(f)
Dfx <-D(fx,"x"); Df <- function(x) eval(Dfx)
plot(Df,a,b,add=TRUE,col="blue")
If <- function(x) integrate(f,0,x)$value
for(i in 0:1000){x<-a+(b-a)/1000*i;points(x,If(x),pch=".",col="red")}
abline(v=c(0.75,1.32,1.83,2.39,3.31,3.85),lty=3,col="green4")
q(1-1E-2);q(1-1E-5);q(1-1E-10)
[1] -199
[1] -199999
[1] -Inf
q(1+1E-2);q(1+1E-5);q(1+1E-10)
[1] 201
[1] 200001
[1] Inf
#
# Un altro esempio. Lo studio, data una funzione f, dei punti di flesso
# che assume in [0,5] la sua primitiva F avente valore 0 in 0. Qui i
# valori sono trovati arrotondati ai centesimi (sono tracciate in verde
# scuro le rette verticali che li hanno come ascissa: vedi l'ultimo
# comando "abline").
f <- function(x) x+sin(x)^4*cos(x)^5*60
a <- 0; b <- 5
plot(f,a,b,ylim=c(-7,10)); abline(h=0)
abline(v=c(0,1,2,3,4,5),lty=3,col="grey")
fx <- body(f)
Dfx <-D(fx,"x"); Df <- function(x) eval(Dfx)
plot(Df,a,b,add=TRUE,col="blue")
If <- function(x) integrate(f,0,x)$value
for(i in 0:1000){x<-a+(b-a)/1000*i;points(x,If(x),pch=".",col="red")}
abline(v=c(0.75,1.32,1.83,2.39,3.31,3.85),lty=3,col="green4")
 #
# Lo studio di una serie: 1-1/2+1/3-1/4+1/5...
a <- function(n) (-1)^(n+1)/n # a(n) elemento n-esimo della sommatoria
N <- function(n) seq(1,n,1) # N = 1 2 ... n
S <- function(n) sum(a(N(n))) # somma a(1)+...a(n)
NMax <- 20; y1 <- 0; y2 <- 1 # parte di piano che scelgo
plot(c(0,NMax),c(y1,y2),type="n",xlab="", ylab="")
for(i in 1:NMax) points(i,S(i),pch=".", cex=3)
for(i in 1:(NMax-1)) lines(c(i,i+1),c(S(i),S(i+1)),lty=3)
#
# Lo studio di una serie: 1-1/2+1/3-1/4+1/5...
a <- function(n) (-1)^(n+1)/n # a(n) elemento n-esimo della sommatoria
N <- function(n) seq(1,n,1) # N = 1 2 ... n
S <- function(n) sum(a(N(n))) # somma a(1)+...a(n)
NMax <- 20; y1 <- 0; y2 <- 1 # parte di piano che scelgo
plot(c(0,NMax),c(y1,y2),type="n",xlab="", ylab="")
for(i in 1:NMax) points(i,S(i),pch=".", cex=3)
for(i in 1:(NMax-1)) lines(c(i,i+1),c(S(i),S(i+1)),lty=3)
 # stampo i valori della sommatoria e del termine successivo
# che verrebbe sommato
n <- 100; S(n);a(n+1)
# 0.6881722 0.00990099
n <- 1e3; S(n);a(n+1)
# ...
n <- 1e7; S(n);a(n+1)
# 0.6931471 1e-07
library(codetools); showTree(log(2))
# 0.693147180559945
#
# È facilmente realizzabile lo studio di serie di Fourier
# (esitono anche specifici comandi per studiarle). Un esempio:
p <- function(x) {f <- 0;
for(i in 0:n) f <- f+sin((2*i+1)*x)/(2*i+1); f <- f*4/pi}
n <- 1; plot(p,-5,10, col="blue",n=1000)
abline(h=0,v=0,lty=2,col="blue")
abline(v=axTicks(1), h=axTicks(2), col="grey",lty=3)
n <- 2; plot(p,-5,10,add=TRUE,col="red",n=1000)
n <- 3; plot(p,-5,10,add=TRUE,col="green",n=1000)
n <- 1000; plot(p,-5,10,add=TRUE,col="brown",n=5000)
# stampo i valori della sommatoria e del termine successivo
# che verrebbe sommato
n <- 100; S(n);a(n+1)
# 0.6881722 0.00990099
n <- 1e3; S(n);a(n+1)
# ...
n <- 1e7; S(n);a(n+1)
# 0.6931471 1e-07
library(codetools); showTree(log(2))
# 0.693147180559945
#
# È facilmente realizzabile lo studio di serie di Fourier
# (esitono anche specifici comandi per studiarle). Un esempio:
p <- function(x) {f <- 0;
for(i in 0:n) f <- f+sin((2*i+1)*x)/(2*i+1); f <- f*4/pi}
n <- 1; plot(p,-5,10, col="blue",n=1000)
abline(h=0,v=0,lty=2,col="blue")
abline(v=axTicks(1), h=axTicks(2), col="grey",lty=3)
n <- 2; plot(p,-5,10,add=TRUE,col="red",n=1000)
n <- 3; plot(p,-5,10,add=TRUE,col="green",n=1000)
n <- 1000; plot(p,-5,10,add=TRUE,col="brown",n=5000)
 # Per n=1000 ci si avvicina alla "somma", volendo tracciabile con i
# comandi seguenti ( quad(x) riconduce x a [-pi,pi) )
quad <- function(x) {y <- floor(x/(2*pi)); y <- x-y*2*pi;
y <- y-2*pi*ifelse(y >= pi,1,0); y }
F <- function(x) {x <- quad(x);
ifelse(0 < x & x < pi,1,ifelse(-pi < x & x <0,-1,0))}
plot(F,-5,10,add=TRUE,n=1000,col="grey50")
#
# grafico di una funzione di 2 variabili (x,y)-> sin(x)+cos(2y)
# theta, phi e d indicano la posizione dell'occhio: la direzione dello
# sguardo proiettata sul piano orizzontale, la sua inclinazione rispetto
# a tale piano e la distanza dell'occhio dal centro del box. La figura
# seguente figura illustra il significato di theta e di phi:
# Per n=1000 ci si avvicina alla "somma", volendo tracciabile con i
# comandi seguenti ( quad(x) riconduce x a [-pi,pi) )
quad <- function(x) {y <- floor(x/(2*pi)); y <- x-y*2*pi;
y <- y-2*pi*ifelse(y >= pi,1,0); y }
F <- function(x) {x <- quad(x);
ifelse(0 < x & x < pi,1,ifelse(-pi < x & x <0,-1,0))}
plot(F,-5,10,add=TRUE,n=1000,col="grey50")
#
# grafico di una funzione di 2 variabili (x,y)-> sin(x)+cos(2y)
# theta, phi e d indicano la posizione dell'occhio: la direzione dello
# sguardo proiettata sul piano orizzontale, la sua inclinazione rispetto
# a tale piano e la distanza dell'occhio dal centro del box. La figura
# seguente figura illustra il significato di theta e di phi:
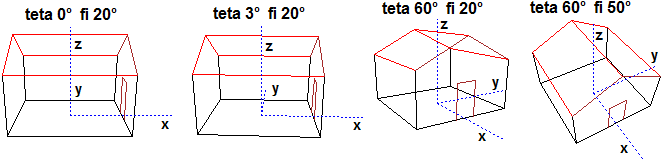 x <- y <- seq(-pi,pi, by=0.2)
f <- function(x,y) sin(x)+cos(2*y)
z <- outer(x,y,f) # crea la matrice z delle altezze
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed")
# a destra il grafico "non colorato"
persp(x,y,z,phi=60,theta=30,d=20,col=NULL,ticktype="detailed")
x <- y <- seq(-pi,pi, by=0.2)
f <- function(x,y) sin(x)+cos(2*y)
z <- outer(x,y,f) # crea la matrice z delle altezze
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed")
# a destra il grafico "non colorato"
persp(x,y,z,phi=60,theta=30,d=20,col=NULL,ticktype="detailed")
 # cosa si otterrebbe con d=1 e (theta,phi) pari a (0,0), (0,90), (90,0):
# cosa si otterrebbe con d=1 e (theta,phi) pari a (0,0), (0,90), (90,0):
 # e le curve di livello
contour(x,y,z)
# e le curve di livello
contour(x,y,z)
 contour(x,y,z,col=heat.colors(12))
contour(x,y,z,zlim=c(0,2))
contour(x,y,z,zlim=c(0,-2))
contour(x,y,z,col=heat.colors(12),nlevels=5)
contour(x,y,z,zlim=c(0,2),nlevels=5)
contour(x,y,z, levels=c(-1,0,0.5,1) )
contour(x,y,z,col=heat.colors(12))
contour(x,y,z,zlim=c(0,2))
contour(x,y,z,zlim=c(0,-2))
contour(x,y,z,col=heat.colors(12),nlevels=5)
contour(x,y,z,zlim=c(0,2),nlevels=5)
contour(x,y,z, levels=c(-1,0,0.5,1) )
 # Altri modi di visulizzare le curve di livello:
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=heat.colors(5) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(3) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(5) )
# Un esempi commentati dettagliatamente li trovi qui e qui
# Altri modi di visulizzare le curve di livello:
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=heat.colors(5) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(3) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(5) )
# Un esempi commentati dettagliatamente li trovi qui e qui
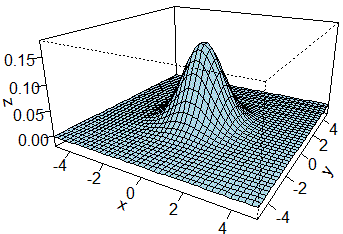 # un altro esempio:
x <- y <- seq(-10, 10, len = 30)
f <- function(x,y) { r <- sqrt(x^2+y^2); 10 * sin(r)/r }
z <- outer(x, y, f)
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
# Volendo posso ridurre i margini (e quindi ingrandire la figura) azionando
# prima: par( mai = c(0.3,0.3,0.3,0.3) ) (vedi)
# un altro esempio:
x <- y <- seq(-10, 10, len = 30)
f <- function(x,y) { r <- sqrt(x^2+y^2); 10 * sin(r)/r }
z <- outer(x, y, f)
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
# Volendo posso ridurre i margini (e quindi ingrandire la figura) azionando
# prima: par( mai = c(0.3,0.3,0.3,0.3) ) (vedi)
 # ottengo la prima figura; la seconda è stata ottenuta aggiungendo le ombre:
persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue", shade=0.4)
# Azionando expand posso modificare i rapporti tra le scale:
persp(x,y,z, theta=30, phi=30, expand=0.25, col="lightblue", shade=0.4)
# ottengo la prima figura; la seconda è stata ottenuta aggiungendo le ombre:
persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue", shade=0.4)
# Azionando expand posso modificare i rapporti tra le scale:
persp(x,y,z, theta=30, phi=30, expand=0.25, col="lightblue", shade=0.4)
 # Usando trans3d() aggiungo dei pezzi, ottenendo la figura a sinistra
# Usando trans3d() aggiungo dei pezzi, ottenendo la figura a sinistra
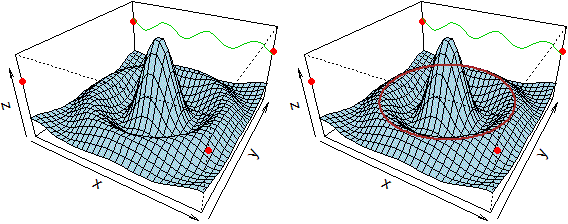 fig <- persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue")
xE <- c(-10,10); xy <- expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = fig), col = 2, pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = fig), col = 3)
# con altri comandi ottengo la figura a destra:
phi <- seq(0, 2*pi, len = 201)
r1 <- 7.725 # raggio del "secondo" massimo
xr <- r1 * cos(phi)
yr <- r1 * sin(phi)
lines(trans3d(xr,yr, f(xr,yr), fig), col = "brown", lwd = 2)
# si è fatto un altro uso di seq
seq(-10, 10, len = 30)
[1] -10.0000000 -9.3103448 -8.6206897 -7.9310345 -7.2413793
[6] -6.5517241 -5.8620690 -5.1724138 -4.4827586 -3.7931034
[11] -3.1034483 -2.4137931 -1.7241379 -1.0344828 -0.3448276
[16] 0.3448276 1.0344828 1.7241379 2.4137931 3.1034483
[21] 3.7931034 4.4827586 5.1724138 5.8620690 6.5517241
[26] 7.2413793 7.9310345 8.6206897 9.3103448 10.0000000
#
# Per il calcolo di gradiente ed hessiano cerca fdHess nell'help di R
# Qui trovi un esempio in cui il gradiente e l'hessiano sono costruiti.
#
# Un'altra figura tridimensionale (xlim,… -vedi- indica l'intervallo per le x,...)
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
persp(x,y,z,theta=-20,phi=25,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
fig <- persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue")
xE <- c(-10,10); xy <- expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = fig), col = 2, pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = fig), col = 3)
# con altri comandi ottengo la figura a destra:
phi <- seq(0, 2*pi, len = 201)
r1 <- 7.725 # raggio del "secondo" massimo
xr <- r1 * cos(phi)
yr <- r1 * sin(phi)
lines(trans3d(xr,yr, f(xr,yr), fig), col = "brown", lwd = 2)
# si è fatto un altro uso di seq
seq(-10, 10, len = 30)
[1] -10.0000000 -9.3103448 -8.6206897 -7.9310345 -7.2413793
[6] -6.5517241 -5.8620690 -5.1724138 -4.4827586 -3.7931034
[11] -3.1034483 -2.4137931 -1.7241379 -1.0344828 -0.3448276
[16] 0.3448276 1.0344828 1.7241379 2.4137931 3.1034483
[21] 3.7931034 4.4827586 5.1724138 5.8620690 6.5517241
[26] 7.2413793 7.9310345 8.6206897 9.3103448 10.0000000
#
# Per il calcolo di gradiente ed hessiano cerca fdHess nell'help di R
# Qui trovi un esempio in cui il gradiente e l'hessiano sono costruiti.
#
# Un'altra figura tridimensionale (xlim,… -vedi- indica l'intervallo per le x,...)
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
persp(x,y,z,theta=-20,phi=25,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
 # la prima e altre due visioni
persp(x,y,z,theta=-45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
persp(x,y,z,theta=45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
# Con l'opzione scale=TRUE, omettibile, la figura è tracciata adattando le
# scale sui vari assi. Invece con scale=FALSE essa non viene diversamente
# scalata (si ha un sistema monometrico). Aggiungendo ticktype="detailed"
# vengono visulizzate delle tacche che consentono di capire il fenomeno.
persp(x,y,z,theta=45,phi=25,col="grey",zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
persp(x,y,z,theta=45,phi=25,col="grey",scale=FALSE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
# la prima e altre due visioni
persp(x,y,z,theta=-45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
persp(x,y,z,theta=45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
# Con l'opzione scale=TRUE, omettibile, la figura è tracciata adattando le
# scale sui vari assi. Invece con scale=FALSE essa non viene diversamente
# scalata (si ha un sistema monometrico). Aggiungendo ticktype="detailed"
# vengono visulizzate delle tacche che consentono di capire il fenomeno.
persp(x,y,z,theta=45,phi=25,col="grey",zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
persp(x,y,z,theta=45,phi=25,col="grey",scale=FALSE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
 # L'immagine sotto (in scala monometrica) è ottenuta aggiungendo un punto e
# una spezzata, usando trans3d per darne le coordinate; per fare l'aggiunta occorre
# memorizzare la prima figura (qui l'abbiamo chiamata A) e poi richiamarla con pmat:
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
zlim=c(0,15),xlim=c(-1,10),ylim=c(-1,10), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
# L'immagine sotto (in scala monometrica) è ottenuta aggiungendo un punto e
# una spezzata, usando trans3d per darne le coordinate; per fare l'aggiunta occorre
# memorizzare la prima figura (qui l'abbiamo chiamata A) e poi richiamarla con pmat:
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
zlim=c(0,15),xlim=c(-1,10),ylim=c(-1,10), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
 # Sopra a destra l'immagine riducendo con nticks il numero delle tacche:
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
nticks=3,zlim=c(0,15),xlim=c(-1,11),ylim=c(-1,11), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
#
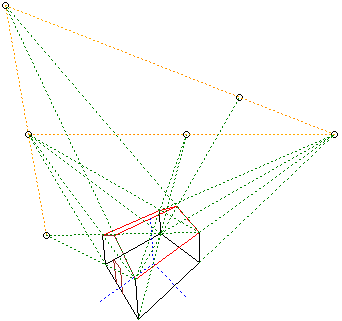
# Un altro esempio (vedi qui o qui, o qui): una casetta (fatta pezzo
# per pezzo) e i "punti all'infinito"
# Sopra a destra l'immagine riducendo con nticks il numero delle tacche:
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
nticks=3,zlim=c(0,15),xlim=c(-1,11),ylim=c(-1,11), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
#
# Un altro esempio (vedi qui o qui, o qui): una casetta (fatta pezzo
# per pezzo) e i "punti all'infinito"

 # Altro esempio con spiegazioni dettagliate
#
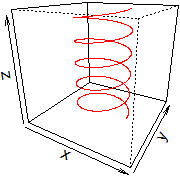
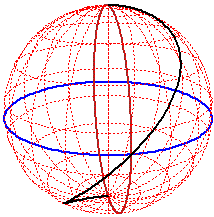
# Una curva nello spazio (5 giri di un'elica)
t <- seq(0,10*pi,len=1000)
z0 <- c(0,10*pi); u <- rep(z0[1],4) # metto in u la base del box
z <- array(u,dim=c(2,2)); x <- c(-2,2); y <- c(-2,2)
F <- persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# per averla senza box avrei aggiunto in persp: border="white",box=FALSE)
# Altro esempio con spiegazioni dettagliate
#
# Una curva nello spazio (5 giri di un'elica)
t <- seq(0,10*pi,len=1000)
z0 <- c(0,10*pi); u <- rep(z0[1],4) # metto in u la base del box
z <- array(u,dim=c(2,2)); x <- c(-2,2); y <- c(-2,2)
F <- persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# per averla senza box avrei aggiunto in persp: border="white",box=FALSE)

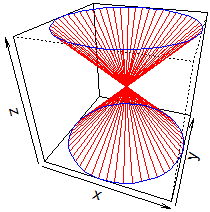 # Sopra al centro un'altra figura (qui) e a destra un'altra (qui)
#
# Sotto a sinistra la terra e la rotta longitudine=latitudine (vedi).
# Un'ulteriore figura (volcano), a destra, già memorizzata nel programma
z <- 3 * volcano # moltiplico per 3 i dati
y <- 10 * (1:ncol(z)) # 10 meter spacing (E to W)
x <- 10 * (1:nrow(z)) # 10 meter spacing (S to N)
par(bg = "grey")
persp(x,y,z,theta=135,phi=30,col="green3",scale=FALSE,ltheta=-120,shade=0.75,border=NA,box=FALSE)
# Sopra al centro un'altra figura (qui) e a destra un'altra (qui)
#
# Sotto a sinistra la terra e la rotta longitudine=latitudine (vedi).
# Un'ulteriore figura (volcano), a destra, già memorizzata nel programma
z <- 3 * volcano # moltiplico per 3 i dati
y <- 10 * (1:ncol(z)) # 10 meter spacing (E to W)
x <- 10 * (1:nrow(z)) # 10 meter spacing (S to N)
par(bg = "grey")
persp(x,y,z,theta=135,phi=30,col="green3",scale=FALSE,ltheta=-120,shade=0.75,border=NA,box=FALSE)
 # la "corretta" rappresentazione prospettica consente significative
# attività matematiche; un esempio:
# una parabola che sembra un'ellisse (lo spazio è [0,10]*[0,10]*[0,10]):
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=FALSE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# la "corretta" rappresentazione prospettica consente significative
# attività matematiche; un esempio:
# una parabola che sembra un'ellisse (lo spazio è [0,10]*[0,10]*[0,10]):
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=FALSE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
 x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=TRUE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# visione con phi=5; ecco che cosa si ottiene con phi=45 e con phi=60:
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=TRUE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# visione con phi=5; ecco che cosa si ottiene con phi=45 e con phi=60:
 # proc.time() fornisce l'ora (dall'avvio del programma), con [3] i secondi
# Per avere data ed ora occorre invece usare date() (si ha una uscita
# come: "Mon Dec 19 17:55:38 2011" ). Per altri modi per avere l'ora vedi
# (qui trovi anche come trasformare un numero tra virgolette in un numero).
# Ecco un contasecondi. Per arrestarlo premi il tasto ESC. In modo analogo
# si possono creare animazioni dei più vari tipi.
# tic(x) fa passare x sec; plot(...) prepara lo schermo; la 3^a e' l'orologio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec}
plot(c(0,1),c(0,1),xlab="", ylab="", col="white", col.axis="white"); i<-0
while(1<2){rect(0,0,1,1,col="yellow"); text(0.5,0.1,i); tic(1); i<-i+1}
# proc.time() fornisce l'ora (dall'avvio del programma), con [3] i secondi
# Per avere data ed ora occorre invece usare date() (si ha una uscita
# come: "Mon Dec 19 17:55:38 2011" ). Per altri modi per avere l'ora vedi
# (qui trovi anche come trasformare un numero tra virgolette in un numero).
# Ecco un contasecondi. Per arrestarlo premi il tasto ESC. In modo analogo
# si possono creare animazioni dei più vari tipi.
# tic(x) fa passare x sec; plot(...) prepara lo schermo; la 3^a e' l'orologio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec}
plot(c(0,1),c(0,1),xlab="", ylab="", col="white", col.axis="white"); i<-0
while(1<2){rect(0,0,1,1,col="yellow"); text(0.5,0.1,i); tic(1); i<-i+1}
 # Qui trovi come ottenere la seguente animazione
# Qui trovi come ottenere la seguente animazione
 | → |  |
# Qui come ottenere questa, a sinistra:

 # Qui come ottenere l'animazione di cui quella sopra a destra è un'istantanea
#
# Inserire locator(1) è un altro modo, molto comodo, per realizzare delle
# animazioni: occorre fare un CLIC per passare alla immagine successiva
# (title consente di mettere un titolo alla finestra; locator all'interno
# di parentesi grafiche non visualizza le coordinate del punto cliccato)
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f)
# clicca man mano la figura (se vuoi finire prima premi ESC)
for(a in -90:90) { persp(x,y,z, theta=30, phi = a, expand=0.5, col="green");
title(paste(a,"°")); locator(1) }
# Qui come ottenere l'animazione di cui quella sopra a destra è un'istantanea
#
# Inserire locator(1) è un altro modo, molto comodo, per realizzare delle
# animazioni: occorre fare un CLIC per passare alla immagine successiva
# (title consente di mettere un titolo alla finestra; locator all'interno
# di parentesi grafiche non visualizza le coordinate del punto cliccato)
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f)
# clicca man mano la figura (se vuoi finire prima premi ESC)
for(a in -90:90) { persp(x,y,z, theta=30, phi = a, expand=0.5, col="green");
title(paste(a,"°")); locator(1) }
 #
# Una animazione orientata col mouse (per finire premi ESC):
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f); teta <- 30; fi <- 40
while(TRUE) { persp(x,y,z, theta=teta, phi=fi, expand=0.5, col="green")
title(paste(teta,"° ",fi,"°")); l <- locator(1); a <- c(l$x,l$y)
fi <- ifelse(a[2] > 0, fi-1,fi+1); teta <- ifelse(a[1] > 0,teta-1,teta+1) }
# Invece di TRUE potevo mettere, ad es., 1 < 2
#
# Qui trovi come ottenere un'animazione relativa al grafico della
# funzione di due variabili considerata sopra.
# Qui trovi come ottenere l'orologio seguente:
#
# Una animazione orientata col mouse (per finire premi ESC):
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f); teta <- 30; fi <- 40
while(TRUE) { persp(x,y,z, theta=teta, phi=fi, expand=0.5, col="green")
title(paste(teta,"° ",fi,"°")); l <- locator(1); a <- c(l$x,l$y)
fi <- ifelse(a[2] > 0, fi-1,fi+1); teta <- ifelse(a[1] > 0,teta-1,teta+1) }
# Invece di TRUE potevo mettere, ad es., 1 < 2
#
# Qui trovi come ottenere un'animazione relativa al grafico della
# funzione di due variabili considerata sopra.
# Qui trovi come ottenere l'orologio seguente:
 # Qui trovi un esempio relativo al concetto di continuità.
# Qui trovi un altro esempio di animazione; copia l'intero file e
# incollalo in R; ottieni la generazione passo passo della figura
# seguente a sinistra; con questo ottieni quella a destra.
# Qui trovi un esempio relativo al concetto di continuità.
# Qui trovi un altro esempio di animazione; copia l'intero file e
# incollalo in R; ottieni la generazione passo passo della figura
# seguente a sinistra; con questo ottieni quella a destra.
 # Ovviamente potrei ottenere i valori direttamente, a passi:
f <- function(x) x^2; x0 <- 2
h<- 10^-1; (f(x0+h)-f(x0))/h
[1] 4.1
...
h<- 10^-6; (f(x0+h)-f(x0))/h
[1] 4.000001
h<- 10^-7; (f(x0+h)-f(x0))/h
[1] 4
# o direttamente:
D(expression(x^2),"x")
2 * x
# O, per es., potrei procedere così ottenendo:
# Ovviamente potrei ottenere i valori direttamente, a passi:
f <- function(x) x^2; x0 <- 2
h<- 10^-1; (f(x0+h)-f(x0))/h
[1] 4.1
...
h<- 10^-6; (f(x0+h)-f(x0))/h
[1] 4.000001
h<- 10^-7; (f(x0+h)-f(x0))/h
[1] 4
# o direttamente:
D(expression(x^2),"x")
2 * x
# O, per es., potrei procedere così ottenendo:
 # Un esempio di comando su più righe; viene generata una animazione di 1500
# immagini, di cui sotto sono riportate l'inziale ("altezza" di 5°), una
# intermedia, la finale (35°). Copia tutte le righe, incollale in R e fai ACapo
# (è la stessa immagine considerata sopra)
# Inizio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
plot(c(0,10),c(0,10),type="n",xlab="",ylab="")
text(5,6,"E' un'ELLISSE o una PARABOLA ?"); text(5,4,"Osserva l'animazione e rispondi")
tic(5); n<- 200; i<-0; for (k in 0:n) {tic(0.1);x <- c(0,10); y <- c(0,10);
{z <- array(c(0,0,0,0),dim=c(2,2))};
{pr<- persp(x,y,z,xlim=c(0,10),ylim=c(0,10),zlim=c(0,10),phi=0+i,theta=-30)};
{x<-seq(-20,30,len=200);lines(trans3d(x,z=0,y=(x-5)^2,pmat=pr),col="red");i<-i+40/n}}
tic(2); i<-0; for (k in 0:n) {tic(0.03);x <- c(0,10); y <- c(0,10);
{z <- array(c(0,0,0,0),dim=c(2,2))};
{pr<- persp(x,y,z,xlim=c(0,10),ylim=c(0,10),zlim=c(0,10),phi=40-i,theta=-30)};
{x<-seq(-20,30,len=200);lines(trans3d(x,z=0,y=(x-5)^2,pmat=pr),col="red");i<-i+40/n}}
# Fine
# Un esempio di comando su più righe; viene generata una animazione di 1500
# immagini, di cui sotto sono riportate l'inziale ("altezza" di 5°), una
# intermedia, la finale (35°). Copia tutte le righe, incollale in R e fai ACapo
# (è la stessa immagine considerata sopra)
# Inizio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
plot(c(0,10),c(0,10),type="n",xlab="",ylab="")
text(5,6,"E' un'ELLISSE o una PARABOLA ?"); text(5,4,"Osserva l'animazione e rispondi")
tic(5); n<- 200; i<-0; for (k in 0:n) {tic(0.1);x <- c(0,10); y <- c(0,10);
{z <- array(c(0,0,0,0),dim=c(2,2))};
{pr<- persp(x,y,z,xlim=c(0,10),ylim=c(0,10),zlim=c(0,10),phi=0+i,theta=-30)};
{x<-seq(-20,30,len=200);lines(trans3d(x,z=0,y=(x-5)^2,pmat=pr),col="red");i<-i+40/n}}
tic(2); i<-0; for (k in 0:n) {tic(0.03);x <- c(0,10); y <- c(0,10);
{z <- array(c(0,0,0,0),dim=c(2,2))};
{pr<- persp(x,y,z,xlim=c(0,10),ylim=c(0,10),zlim=c(0,10),phi=40-i,theta=-30)};
{x<-seq(-20,30,len=200);lines(trans3d(x,z=0,y=(x-5)^2,pmat=pr),col="red");i<-i+40/n}}
# Fine
 # Ecco una visione animata della stessa immagine guidata col mouse.
# Cliccando abbassa il punto di vista. Per smettere premi ESC
z <- array(c(0,0,0,0),dim=c(2,2))
teta <- 5; fi <- 50
while(1 < 2) {
pr<- persp(c(0,10),c(0,10),z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",
ylab="y",zlab="z",border="grey",phi=fi,theta=teta,box=FALSE,scale=TRUE,d=2)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
l <- locator(1); a <- c(l$x,l$y); fi <- ifelse(a[2] > 0, fi-1,fi+1)
teta <- ifelse(a[1] > 0,teta-1,teta+1); title(paste(teta,"° ",fi,"°")) }
#
# un altro esempio di ciclo di più righe (copia tutte le righe e
# incollale in R); è il calcolo dell'area di un cerchio approssimata
# per difetto e per eccesso mediante quadrettatura:
# Ecco una visione animata della stessa immagine guidata col mouse.
# Cliccando abbassa il punto di vista. Per smettere premi ESC
z <- array(c(0,0,0,0),dim=c(2,2))
teta <- 5; fi <- 50
while(1 < 2) {
pr<- persp(c(0,10),c(0,10),z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",
ylab="y",zlab="z",border="grey",phi=fi,theta=teta,box=FALSE,scale=TRUE,d=2)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
l <- locator(1); a <- c(l$x,l$y); fi <- ifelse(a[2] > 0, fi-1,fi+1)
teta <- ifelse(a[1] > 0,teta-1,teta+1); title(paste(teta,"° ",fi,"°")) }
#
# un altro esempio di ciclo di più righe (copia tutte le righe e
# incollale in R); è il calcolo dell'area di un cerchio approssimata
# per difetto e per eccesso mediante quadrettatura:
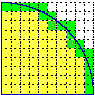 n <- 10
min<- 0; mag<-0; L<-1/n; for(i in 0:n) {for(j in 0:n) { #inizio
{x <- i*L; y <- j*L; d <- x*x+y*y}
{if(i>0 & j>0 & d<=1) min<-min+1; if (d<1) mag<-mag+1}}}
{r <- c(min/n^2*4, mag/n^2*4, (mag-min)/n^2*4)}; r; alarm() #fine
[1] 2.68 3.44 0.76
n <- 100
[1] 3.1016 3.1796 0.0780
n <- 200
[1] 3.1207 3.1602 0.0395
n <- 400
[1] 3.131400 3.151275 0.019875
# alarm(), se l'altoparlante del computer è attivato, produce
# un suono: può essere comodo per segnalare la fine di un ciclo.
#
# Si possono realizzare dei programmini per operare su piu' cifre.
# Vediamo ad es. come fare la somma tra interi di dimensioni qualunque:
x <- c(1,2,3,4); y <- c(1,2,3,4,5)
somma <- function(x,y) {z <- x
m <- length(x); n <- length(y)
# aggiungo degli 0 iniziali al numero piu' corto
if(m > n) y <- c(rep(0,times=m-n),y)
if(n > m) x <- c(rep(0,times=n-m),x)
n <- max(n,m)
# sommo le cifre e 1 se la somma delle precedenti cifre era > 9
r <- 0; for(i in n:1) { w <- x[i]+y[i]+r;
r <- ifelse (w>9,1,0); z[i] <- w-10*r}
if (r > 0) {n <- n+1; for(i in n:1) z[i+1] <- z[i]; z[1] <- 1}
z[1:n] }
somma(x,y)
[1] 1 3 5 7 9
# Possiamo copiarci le righe che definiscono "somma" e applicarle
per fare i calcoli che ci interessano
n <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
somma(n,n)
[1] 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0
# Quanto fa 2 alla 1000? Faccio 1000 raddoppi a partire da 1.
n <- c(1); for (t in 1:1000) {n <- somma(n,n)}; n
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
[31] 0 0 0 1 8 1 0 5 6 1 4 0 4 8 1 1 7 0 5 5 3 3 6 0 7 4 4 3 7 5
[61] 0 3 8 8 3 7 0 3 5 1 0 5 1 1 2 4 9 3 6 1 2 2 4 9 3 1 9 8 3 7
[91] 8 8 1 5 6 9 5 8 5 8 1 2 7 5 9 4 6 7 2 9 1 7 5 5 3 1 4 6 8 2
[121] 5 1 8 7 1 4 5 2 8 5 6 9 2 3 1 4 0 4 3 5 9 8 4 5 7 7 5 7 4 6
[151] 9 8 5 7 4 8 0 3 9 3 4 5 6 7 7 7 4 8 2 4 2 3 0 9 8 5 4 2 1 0
[181] 7 4 6 0 5 0 6 2 3 7 1 1 4 1 8 7 7 9 5 4 1 8 2 1 5 3 0 4 6 4
[211] 7 4 9 8 3 5 8 1 9 4 1 2 6 7 3 9 8 7 6 7 5 5 9 1 6 5 5 4 3 9
[241] 4 6 0 7 7 0 6 2 9 1 4 5 7 1 1 9 6 4 7 7 6 8 6 5 4 2 1 6 7 6
[271] 6 0 4 2 9 8 3 1 6 5 2 6 2 4 3 8 6 8 3 7 2 0 5 6 6 8 0 6 9 3
[301] 7 6
print(2^1000, 16) # controllo:
[1] 1.071508607186267e+301
# Vediamo ora come fare il prodotto tra interi di dimensioni qualunque:
prod <- function(a,b) {
# n = lungh. del numero piu' corto, a1 = num.lungo, b1 = num.corto
if(length(b) < length(a)) {n <- length(b); a1 <- a; b1 <- b}
else {n <- length(a); a1 <- b; b1 <- a}
# somma dei prodotti delle cifre di b1 per a1 (fatti come comme
# ripetute), aggiungendo via via uno 0 ad 1
tot <- 0; for (i in 1:n) {
s <- c(0); k <- n-i+1; if(b1[k] > 0) for(j in 1:b1[k]) s <- somma(s,a1)
a1 <- c(a1,0); tot <- somma(tot,s)}; tot}
u <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
v <- c(9,8,7,6,5,4,3,2,1)
prod(u,v)
[1] 1 2 1 9 3 2 6 3 1 1 2 4 8 2 8 5 3 2 1 1 1 2 6 3 5 2 6 9 0
# Possiamo poi calcolare potenze ad esponente naturale, fattoriali, ...
# Ricalcoliamo 2 alla 1000.
n <- 1; for (t in 1:1000) {n <- prod(n,2)}; n
# Riotteniamo, più lentamente:
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
...
[301] 7 6
# Calcoliamo un fattoriale:
print(factorial(30),16)
[1] 2.652528598121911e+32
p <- 1; for (i in 1:30) p <- prod(p,i); p
[1] 2 6 5 2 5 2 8 5 9 8 1 2 1 9 1 0 5 8 6 3 6 3 0 8 4 8 0 0 0 0 0 0 0
#
# I comandi utf8ToInt e intToUtf8 consentono di esplorare il codice (UTF8,
# simile all'ASCII) usato per codificare numericamente i caratteri (numeri
# in base 2, visualizzati in base dieci):
utf8ToInt("("); utf8ToInt("MaCoSa")
[1] 40
[1] 77 97 67 111 83 97
intToUtf8(40); intToUtf8(c(77,97,67,111,83,97))
[1] "("
[1] "MaCoSa"
# Si possono codificare segretamente i messaggi. Ecco un esempio semplice
# (facilmente "scopribile"): aggiungo 7 ai codici.
utf8ToInt("MaCoSa"); utf8ToInt("MaCoSa")+7
[1] 77 97 67 111 83 97
[1] 84 104 74 118 90 104
cod <- c(84,104,74,118,90,104); intToUtf8(cod); intToUtf8(cod-7)
[1] "ThJvZh"
[1] "MaCoSa"
# Ecco la codifica (32,33,35-91,93-126) dei caratteri usuali:
intToUtf8( c(32,33,seq(35,91)) )
[1] " !#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ["
intToUtf8( seq(93,126) )
[1] "]^_`abcdefghijklmnopqrstuvwxyz{|}~"
utf8ToInt(" 09AZaz")
[1] 32 48 57 65 90 97 122
#
# Un altro esempio di animazione (usa una finestra non troppo piccola):
coor <- c(-1,1,0,1); orig <- c(0,0)
yy <- c(-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1); xx <- c(0,0.25,0.5,0.75,1)
ce <- function(x) sqrt(1-(x^2))
n <- 30; for (i in 0:n) #inizio
{{plot(c(coor[1],coor[2]),c(coor[3],coor[4]),type="n",xlab="",ylab="",asp=1)}
{abline(h=xx,col="grey");abline(v=yy,col="grey");abline(h=0,col="blue")}
{curve(ce, add=TRUE,col="blue");x<-cos(pi/n*i);y<-sin(pi/n*i)}
{x1 <- c(-1,x,1); y1 <- c(0,y,0);lines(x1,y1);points(x*0.9,y*0.9)}
text(-7/8,0.9,"clicca"); locator(1)} #fine
n <- 10
min<- 0; mag<-0; L<-1/n; for(i in 0:n) {for(j in 0:n) { #inizio
{x <- i*L; y <- j*L; d <- x*x+y*y}
{if(i>0 & j>0 & d<=1) min<-min+1; if (d<1) mag<-mag+1}}}
{r <- c(min/n^2*4, mag/n^2*4, (mag-min)/n^2*4)}; r; alarm() #fine
[1] 2.68 3.44 0.76
n <- 100
[1] 3.1016 3.1796 0.0780
n <- 200
[1] 3.1207 3.1602 0.0395
n <- 400
[1] 3.131400 3.151275 0.019875
# alarm(), se l'altoparlante del computer è attivato, produce
# un suono: può essere comodo per segnalare la fine di un ciclo.
#
# Si possono realizzare dei programmini per operare su piu' cifre.
# Vediamo ad es. come fare la somma tra interi di dimensioni qualunque:
x <- c(1,2,3,4); y <- c(1,2,3,4,5)
somma <- function(x,y) {z <- x
m <- length(x); n <- length(y)
# aggiungo degli 0 iniziali al numero piu' corto
if(m > n) y <- c(rep(0,times=m-n),y)
if(n > m) x <- c(rep(0,times=n-m),x)
n <- max(n,m)
# sommo le cifre e 1 se la somma delle precedenti cifre era > 9
r <- 0; for(i in n:1) { w <- x[i]+y[i]+r;
r <- ifelse (w>9,1,0); z[i] <- w-10*r}
if (r > 0) {n <- n+1; for(i in n:1) z[i+1] <- z[i]; z[1] <- 1}
z[1:n] }
somma(x,y)
[1] 1 3 5 7 9
# Possiamo copiarci le righe che definiscono "somma" e applicarle
per fare i calcoli che ci interessano
n <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
somma(n,n)
[1] 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0
# Quanto fa 2 alla 1000? Faccio 1000 raddoppi a partire da 1.
n <- c(1); for (t in 1:1000) {n <- somma(n,n)}; n
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
[31] 0 0 0 1 8 1 0 5 6 1 4 0 4 8 1 1 7 0 5 5 3 3 6 0 7 4 4 3 7 5
[61] 0 3 8 8 3 7 0 3 5 1 0 5 1 1 2 4 9 3 6 1 2 2 4 9 3 1 9 8 3 7
[91] 8 8 1 5 6 9 5 8 5 8 1 2 7 5 9 4 6 7 2 9 1 7 5 5 3 1 4 6 8 2
[121] 5 1 8 7 1 4 5 2 8 5 6 9 2 3 1 4 0 4 3 5 9 8 4 5 7 7 5 7 4 6
[151] 9 8 5 7 4 8 0 3 9 3 4 5 6 7 7 7 4 8 2 4 2 3 0 9 8 5 4 2 1 0
[181] 7 4 6 0 5 0 6 2 3 7 1 1 4 1 8 7 7 9 5 4 1 8 2 1 5 3 0 4 6 4
[211] 7 4 9 8 3 5 8 1 9 4 1 2 6 7 3 9 8 7 6 7 5 5 9 1 6 5 5 4 3 9
[241] 4 6 0 7 7 0 6 2 9 1 4 5 7 1 1 9 6 4 7 7 6 8 6 5 4 2 1 6 7 6
[271] 6 0 4 2 9 8 3 1 6 5 2 6 2 4 3 8 6 8 3 7 2 0 5 6 6 8 0 6 9 3
[301] 7 6
print(2^1000, 16) # controllo:
[1] 1.071508607186267e+301
# Vediamo ora come fare il prodotto tra interi di dimensioni qualunque:
prod <- function(a,b) {
# n = lungh. del numero piu' corto, a1 = num.lungo, b1 = num.corto
if(length(b) < length(a)) {n <- length(b); a1 <- a; b1 <- b}
else {n <- length(a); a1 <- b; b1 <- a}
# somma dei prodotti delle cifre di b1 per a1 (fatti come comme
# ripetute), aggiungendo via via uno 0 ad 1
tot <- 0; for (i in 1:n) {
s <- c(0); k <- n-i+1; if(b1[k] > 0) for(j in 1:b1[k]) s <- somma(s,a1)
a1 <- c(a1,0); tot <- somma(tot,s)}; tot}
u <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
v <- c(9,8,7,6,5,4,3,2,1)
prod(u,v)
[1] 1 2 1 9 3 2 6 3 1 1 2 4 8 2 8 5 3 2 1 1 1 2 6 3 5 2 6 9 0
# Possiamo poi calcolare potenze ad esponente naturale, fattoriali, ...
# Ricalcoliamo 2 alla 1000.
n <- 1; for (t in 1:1000) {n <- prod(n,2)}; n
# Riotteniamo, più lentamente:
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
...
[301] 7 6
# Calcoliamo un fattoriale:
print(factorial(30),16)
[1] 2.652528598121911e+32
p <- 1; for (i in 1:30) p <- prod(p,i); p
[1] 2 6 5 2 5 2 8 5 9 8 1 2 1 9 1 0 5 8 6 3 6 3 0 8 4 8 0 0 0 0 0 0 0
#
# I comandi utf8ToInt e intToUtf8 consentono di esplorare il codice (UTF8,
# simile all'ASCII) usato per codificare numericamente i caratteri (numeri
# in base 2, visualizzati in base dieci):
utf8ToInt("("); utf8ToInt("MaCoSa")
[1] 40
[1] 77 97 67 111 83 97
intToUtf8(40); intToUtf8(c(77,97,67,111,83,97))
[1] "("
[1] "MaCoSa"
# Si possono codificare segretamente i messaggi. Ecco un esempio semplice
# (facilmente "scopribile"): aggiungo 7 ai codici.
utf8ToInt("MaCoSa"); utf8ToInt("MaCoSa")+7
[1] 77 97 67 111 83 97
[1] 84 104 74 118 90 104
cod <- c(84,104,74,118,90,104); intToUtf8(cod); intToUtf8(cod-7)
[1] "ThJvZh"
[1] "MaCoSa"
# Ecco la codifica (32,33,35-91,93-126) dei caratteri usuali:
intToUtf8( c(32,33,seq(35,91)) )
[1] " !#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ["
intToUtf8( seq(93,126) )
[1] "]^_`abcdefghijklmnopqrstuvwxyz{|}~"
utf8ToInt(" 09AZaz")
[1] 32 48 57 65 90 97 122
#
# Un altro esempio di animazione (usa una finestra non troppo piccola):
coor <- c(-1,1,0,1); orig <- c(0,0)
yy <- c(-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1); xx <- c(0,0.25,0.5,0.75,1)
ce <- function(x) sqrt(1-(x^2))
n <- 30; for (i in 0:n) #inizio
{{plot(c(coor[1],coor[2]),c(coor[3],coor[4]),type="n",xlab="",ylab="",asp=1)}
{abline(h=xx,col="grey");abline(v=yy,col="grey");abline(h=0,col="blue")}
{curve(ce, add=TRUE,col="blue");x<-cos(pi/n*i);y<-sin(pi/n*i)}
{x1 <- c(-1,x,1); y1 <- c(0,y,0);lines(x1,y1);points(x*0.9,y*0.9)}
text(-7/8,0.9,"clicca"); locator(1)} #fine
 # calcolo vettoriale
view <- c(-5,5, -5,5); orig <- c(0,0)
tx <- c(-5,-4,-3,-2,-1,0,1,2,3,4,5); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="",asp=1)
abline(h = ty,col="grey"); abline(v = tx, col="grey")
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
vect<- function(v,c) {lines(c(v[1],v[3]),c(v[2],v[4]),col=c);points(v[3],v[4],pch=".", cex=4,col=c)}
plus <- function(v,u) v+u-c(v[3],v[4])
v1 <- c(0,0,2,3); vect(v1,"blue")
v2 <- c(2,3,4,-1); vect(v2,"blue")
vect(plus(v1,v2),"red")
v3 <- c(2,4,4,2); vect(v3,"green4")
v4 <- c(4,2,-2,-3); vect(v4,"green4")
vect(plus(v3,v4),"orange3")
vect(-v2,"black")
# calcolo vettoriale
view <- c(-5,5, -5,5); orig <- c(0,0)
tx <- c(-5,-4,-3,-2,-1,0,1,2,3,4,5); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="",asp=1)
abline(h = ty,col="grey"); abline(v = tx, col="grey")
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
vect<- function(v,c) {lines(c(v[1],v[3]),c(v[2],v[4]),col=c);points(v[3],v[4],pch=".", cex=4,col=c)}
plus <- function(v,u) v+u-c(v[3],v[4])
v1 <- c(0,0,2,3); vect(v1,"blue")
v2 <- c(2,3,4,-1); vect(v2,"blue")
vect(plus(v1,v2),"red")
v3 <- c(2,4,4,2); vect(v3,"green4")
v4 <- c(4,2,-2,-3); vect(v4,"green4")
vect(plus(v3,v4),"orange3")
vect(-v2,"black")
 # alternativa usando il comando arrows (in cui metto
# in ordine le coordinate del 1º e del 2º punto)
view <- c(-2,8, -2,8); orig <- c(0,0)
tx <- seq(-2,8,1); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="", asp=1)
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
abline(h=orig[2],col="brown"); abline(v=orig[1],col="brown")
# length lughezza dei lati della freccia in pollici
v1 <- c(2,3,6,7); c1 <- "red"
v2 <- c(6,7,7,1); c2 <- "brown"
v3 <- c(2,3,7,1); c3 <- "blue"
v<- v1; color<- c1; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v2; color<- c2; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v3; color<- c3; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
# alternativa usando il comando arrows (in cui metto
# in ordine le coordinate del 1º e del 2º punto)
view <- c(-2,8, -2,8); orig <- c(0,0)
tx <- seq(-2,8,1); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="", asp=1)
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
abline(h=orig[2],col="brown"); abline(v=orig[1],col="brown")
# length lughezza dei lati della freccia in pollici
v1 <- c(2,3,6,7); c1 <- "red"
v2 <- c(6,7,7,1); c2 <- "brown"
v3 <- c(2,3,7,1); c3 <- "blue"
v<- v1; color<- c1; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v2; color<- c2; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v3; color<- c3; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
 #
# funzioni polinomiali di 2° grado (parabole) approssimanti dati (vedi)
#
# funzioni polinomiali di 2° grado (parabole) approssimanti dati (vedi)
 # interpolazione con spline (vedi)
# interpolazione con spline (vedi)
 # altro esempio (vedi)
# altro esempio (vedi)
 # medie mobili (vedi)
# medie mobili (vedi)

 #
# Vedi qui per la programmazione lineare
#
# Vedi qui per la matematica finanziaria
#
# un "cuore" (i colori in formato RGB: vedi)
# (ottenuto come fascio di curve di livello)
f <- function(x,y) x^2+((x^2)^(1/3)-y)^2
x <- seq(-20, 20, len=200)
y <- seq(-18, 20, len=200)
z <- outer(x, y, f)
contour(x,y,z,col="#FF8888",zlim=c(100,200),drawlabels=FALSE,nlev=100)
contour(x,y,z,col="#FF0000",zlim=c(200,300),drawlabels=FALSE,nlev=100,add=TRUE)
#
# Vedi qui per la programmazione lineare
#
# Vedi qui per la matematica finanziaria
#
# un "cuore" (i colori in formato RGB: vedi)
# (ottenuto come fascio di curve di livello)
f <- function(x,y) x^2+((x^2)^(1/3)-y)^2
x <- seq(-20, 20, len=200)
y <- seq(-18, 20, len=200)
z <- outer(x, y, f)
contour(x,y,z,col="#FF8888",zlim=c(100,200),drawlabels=FALSE,nlev=100)
contour(x,y,z,col="#FF0000",zlim=c(200,300),drawlabels=FALSE,nlev=100,add=TRUE)
 # un'altra animazione:
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
view <- c(0,100, 0,70)
for (k in 59:0) {plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="") #inizio
abline(h=k+1,col="blue");abline(h=k+1.25,col="blue");abline(h=k+1.5,col="blue")
if (k>0) for (i in 1:99) for (j in 1:k) if (runif(1)<0.03) points(i,j,col="blue");tic(0.3)} #fine
# un'altra animazione:
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
view <- c(0,100, 0,70)
for (k in 59:0) {plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="") #inizio
abline(h=k+1,col="blue");abline(h=k+1.25,col="blue");abline(h=k+1.5,col="blue")
if (k>0) for (i in 1:99) for (j in 1:k) if (runif(1)<0.03) points(i,j,col="blue");tic(0.3)} #fine
 #
# Per inciso, osserviamo che si possono realizzare grafi ad albero in
# vari modi. Si veda l'help in linea per dettagli. Qui vediamo solo
# come realizzare grafi opportunamente "bilanciati" caricando la libreria
# "cluster" e utilizzando il comando pltree (e il comando agnes:
# Agglomerative Nesting):
library(cluster)
cosa <- c(1,2,3,4,5,6,7,8)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9,10)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
#
# Per inciso, osserviamo che si possono realizzare grafi ad albero in
# vari modi. Si veda l'help in linea per dettagli. Qui vediamo solo
# come realizzare grafi opportunamente "bilanciati" caricando la libreria
# "cluster" e utilizzando il comando pltree (e il comando agnes:
# Agglomerative Nesting):
library(cluster)
cosa <- c(1,2,3,4,5,6,7,8)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9,10)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
 cosa <- c(1,1,2,2,3)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,2,3,3,4,4)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,1,2,2,3,3,4,5); Cosa <- c("a","a","b","b","c","c","d","e")
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=Cosa)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=FALSE)
cosa <- c(1,1,2,2,3)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,2,3,3,4,4)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,1,2,2,3,3,4,5); Cosa <- c("a","a","b","b","c","c","d","e")
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=Cosa)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=FALSE)

# Cenni ad impieghi più significativi dei "cluster" li trovi qui.
# Vedi qui per la realizzazione di immagini come le seguenti:

 #
# Come verificare l'equivalenza di 2 termini con più variabili che stanno
# in dati intervalli con il generatore di numeri casuali (se ne hanno
# solo una basta farlo confrontandone i grafici). Esempio:
a1 <- function(x,y) sin(x)-sin(y)
a2 <- function(x,y) 2*sin((x-y)/2)*cos((x+y)/2)
x1 <- -pi; x2 <- 2*pi; x <- x1+runif(12)*(x2-x1)
y1 <- -pi; y2 <- 2*pi; y <- y1+runif(12)*(y2-y1)
a1(x,y); a2(x,y)
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
# Con ulteriori prove ho una conferma (non una prova) dell'equivalenza.
# Per una conferma simbolica posso usare wolframalpha.com: se metto in input
# 2*sin((x-y)/2)*cos((x+y)/2) ottengo la semplificazione sin(x)-sin(y)
# (e molte altre cose ...)
#
# Sui grafici o in pagine apposite posso scrivere formule complesse
# così come le scriverei "a mano". Qualche esempio:
# (bg="…" serve solo per fare giallo lo sfondo)
par( mai = c(0,0,0,0), bg="#FFFF99" )
plot(c(0,10),c(0,10),type="n")
text(2,8,expression(A[2]))
# invece di expression si può usare quote
text(2,5,expression(lim(frac(1,2^n),n %->% infinity)))
text(2,2,expression("k = "*bgroup("(",atop(m,n),")")))
# o text(2,2,expression("k = "~bgroup("(",atop(m,n),")")))
text(5,8,expression(frac(a+b,frac(c+b,2^n))~+1))
text(5,5,expression(integral(f(x)*dx,a,b)))
# il simbolo ~ introduce uno spazio bianco (copialo da qui se non
# riesci a batterlo)
text(5,2,expression(integral(f(x)*~dx,a,b)))
text(8,8,expression(widehat(ABC)))
text(8,5,expression(hat(ABC)))
text(8,2,expression(bar(ABC)))
#
# Come verificare l'equivalenza di 2 termini con più variabili che stanno
# in dati intervalli con il generatore di numeri casuali (se ne hanno
# solo una basta farlo confrontandone i grafici). Esempio:
a1 <- function(x,y) sin(x)-sin(y)
a2 <- function(x,y) 2*sin((x-y)/2)*cos((x+y)/2)
x1 <- -pi; x2 <- 2*pi; x <- x1+runif(12)*(x2-x1)
y1 <- -pi; y2 <- 2*pi; y <- y1+runif(12)*(y2-y1)
a1(x,y); a2(x,y)
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
# Con ulteriori prove ho una conferma (non una prova) dell'equivalenza.
# Per una conferma simbolica posso usare wolframalpha.com: se metto in input
# 2*sin((x-y)/2)*cos((x+y)/2) ottengo la semplificazione sin(x)-sin(y)
# (e molte altre cose ...)
#
# Sui grafici o in pagine apposite posso scrivere formule complesse
# così come le scriverei "a mano". Qualche esempio:
# (bg="…" serve solo per fare giallo lo sfondo)
par( mai = c(0,0,0,0), bg="#FFFF99" )
plot(c(0,10),c(0,10),type="n")
text(2,8,expression(A[2]))
# invece di expression si può usare quote
text(2,5,expression(lim(frac(1,2^n),n %->% infinity)))
text(2,2,expression("k = "*bgroup("(",atop(m,n),")")))
# o text(2,2,expression("k = "~bgroup("(",atop(m,n),")")))
text(5,8,expression(frac(a+b,frac(c+b,2^n))~+1))
text(5,5,expression(integral(f(x)*dx,a,b)))
# il simbolo ~ introduce uno spazio bianco (copialo da qui se non
# riesci a batterlo)
text(5,2,expression(integral(f(x)*~dx,a,b)))
text(8,8,expression(widehat(ABC)))
text(8,5,expression(hat(ABC)))
text(8,2,expression(bar(ABC)))
 # Le stesse cose si ottengono se si usa bquote, che consente anche di sostituire
# valori alle variabili. Un esempio:
text(1.5,1,bquote( integral(F(t)~dt,a,b)~" ="~ F(b) - F(a)))
a=2; text(5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
a="c"; text(8.5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
# Quanto racchiusa in .(…) un'espressione viene visualizzata col suo valore.
# Le stesse cose si ottengono se si usa bquote, che consente anche di sostituire
# valori alle variabili. Un esempio:
text(1.5,1,bquote( integral(F(t)~dt,a,b)~" ="~ F(b) - F(a)))
a=2; text(5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
a="c"; text(8.5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
# Quanto racchiusa in .(…) un'espressione viene visualizzata col suo valore.
 # Sono scritte in Teχ. Vedi qui per altri esempi.
# Sono scritte in Teχ. Vedi qui per altri esempi.
 #
# il programma opera anche sui numeri complessi se compare una "i"
3+sqrt(0.25)
[1] 3.5
3+sqrt(-0.25)
[1] NaN
Warning message:
In sqrt(-0.25) : NaNs produced
# NAN: not a number
3+sqrt(-0.25+0i)
[1] 3+0.5i
z <- 4+3i; Re(z); Im(z); Conj(z)
[1] 4
[1] 3
[1] 4-3i
Mod(z); Arg(z); sqrt(Re(z)^2+Im(z)^2); atan(Im(z)/Re(z))
[1] 5
[1] 0.6435011
[1] 5
[1] 0.6435011
# Vedi qui per come rappresentare graficamente trasformazioni conformi (vedi)
#
# il programma opera anche sui numeri complessi se compare una "i"
3+sqrt(0.25)
[1] 3.5
3+sqrt(-0.25)
[1] NaN
Warning message:
In sqrt(-0.25) : NaNs produced
# NAN: not a number
3+sqrt(-0.25+0i)
[1] 3+0.5i
z <- 4+3i; Re(z); Im(z); Conj(z)
[1] 4
[1] 3
[1] 4-3i
Mod(z); Arg(z); sqrt(Re(z)^2+Im(z)^2); atan(Im(z)/Re(z))
[1] 5
[1] 0.6435011
[1] 5
[1] 0.6435011
# Vedi qui per come rappresentare graficamente trasformazioni conformi (vedi)
 #
# ricordiamo come tracciare curve descritte in forma parametrica:
x1 <- -4; x2 <- 4; y1 <- -4; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="", asp=1)
for(i in (-8:8)/2) abline(h=i,col="grey")
for(i in (-8:8)/2) abline(v=i,col="grey")
abline(h=0,col="brown"); abline(v=0,col="brown")
t1 <- 0; t2 <- 2*pi; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(2*cos(t)+1,3*sin(t)-1, col="blue")
lines(cos(t)+1,3/2*sin(t)-1, col="green")
t1 <- -4; t2 <- 4; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2,t, col="red")
#
# ricordiamo come tracciare curve descritte in forma parametrica:
x1 <- -4; x2 <- 4; y1 <- -4; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="", asp=1)
for(i in (-8:8)/2) abline(h=i,col="grey")
for(i in (-8:8)/2) abline(v=i,col="grey")
abline(h=0,col="brown"); abline(v=0,col="brown")
t1 <- 0; t2 <- 2*pi; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(2*cos(t)+1,3*sin(t)-1, col="blue")
lines(cos(t)+1,3/2*sin(t)-1, col="green")
t1 <- -4; t2 <- 4; punti <- 2001; t <- seq(t1,t2,(t2-t1)/punti)
lines(t^2,t, col="red")
 # Un cerchio e un poligono regolare:
plot(c(-5,7),c(-7,5),type="n",asp=1)
# Togliendo asp=1 posso avere una scala non monometrica
abline(h=axTicks(2),v=axTicks(1),lty=3)
# raggio e centro
r <- 5; C <- c(2,-1); points(C[1],C[2])
t <- seq(0,2*pi,len=5); lines(C[1]+r*cos(t),C[2]+r*sin(t),col="red")
t <- seq(0,2*pi,len=500); lines(C[1]+r*cos(t),C[2]+r*sin(t))
# Un cerchio e un poligono regolare:
plot(c(-5,7),c(-7,5),type="n",asp=1)
# Togliendo asp=1 posso avere una scala non monometrica
abline(h=axTicks(2),v=axTicks(1),lty=3)
# raggio e centro
r <- 5; C <- c(2,-1); points(C[1],C[2])
t <- seq(0,2*pi,len=5); lines(C[1]+r*cos(t),C[2]+r*sin(t),col="red")
t <- seq(0,2*pi,len=500); lines(C[1]+r*cos(t),C[2]+r*sin(t))
 #
# vedi qui per il tracciamento di curve in coordinate polari
#
# vedi qui per il tracciamento di curve in coordinate polari
 #
# Qui come tracciare curve descritte mediante equazioni
#
# Qui come tracciare curve descritte mediante equazioni

 # Qui come risolvere risp. a x o a y equazioni F(x,k) = 0, F(k,y) = 0
#
# Vedi qui per un modo in cui realizzare intersezioni di figure (a sinistra)
# e qui per un altro (a destra). Analogamente posso fare unioni.
# Qui come risolvere risp. a x o a y equazioni F(x,k) = 0, F(k,y) = 0
#
# Vedi qui per un modo in cui realizzare intersezioni di figure (a sinistra)
# e qui per un altro (a destra). Analogamente posso fare unioni.


 #
# in usi di base abbiamo visto come affrontare la risoluzione numerica di
# una qualunque equazione; per le eq. polinomiali possiamo riccorrere a
# polyroot(c(A0,A1,..,An)), dando in input i coefficienti, ordinati (quello
# di grado 0, poi quello di grado 1, quello di grado 2, ...), dei polinomi;
# ad es. per risolvere x^2-1=0, x^3+x^2-x-1=0, 5x^2+2x-5=0 facciamo:
polyroot(c(-1,0,1)); polyroot(c(-1,-1,1,1)); polyroot(c(-5,2,5))
[1] 1+0i -1+0i
[1] 1-0i -1-0i -1+0i
[1] 0.8198039-0i -1.2198039+0i
# le soluzioni sono 1, -1; 1, -1 (-1 punto di tangenza); e
# 0.8198039, -1.2198039; facciamo un controllo grafico:
x1 <- -3; x2 <- 3; y1 <- -5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red");curve(g,add=TRUE,col="blue");curve(h,add=TRUE)
#
# in usi di base abbiamo visto come affrontare la risoluzione numerica di
# una qualunque equazione; per le eq. polinomiali possiamo riccorrere a
# polyroot(c(A0,A1,..,An)), dando in input i coefficienti, ordinati (quello
# di grado 0, poi quello di grado 1, quello di grado 2, ...), dei polinomi;
# ad es. per risolvere x^2-1=0, x^3+x^2-x-1=0, 5x^2+2x-5=0 facciamo:
polyroot(c(-1,0,1)); polyroot(c(-1,-1,1,1)); polyroot(c(-5,2,5))
[1] 1+0i -1+0i
[1] 1-0i -1-0i -1+0i
[1] 0.8198039-0i -1.2198039+0i
# le soluzioni sono 1, -1; 1, -1 (-1 punto di tangenza); e
# 0.8198039, -1.2198039; facciamo un controllo grafico:
x1 <- -3; x2 <- 3; y1 <- -5; y2 <- 4
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red");curve(g,add=TRUE,col="blue");curve(h,add=TRUE)
 # (Otterrei gli stessi risultati mettendo ad es. x^3+x^2-x-1 in WolframAlpha.com)
# Ecco un altro esempio: la soluzione di x^3+3*x+1 = 0
pol <- function(x) 1+3*x+x^3
plot(pol,-3,3); abline(h=0,col="brown"); abline(v=0,col="brown")
# (Otterrei gli stessi risultati mettendo ad es. x^3+x^2-x-1 in WolframAlpha.com)
# Ecco un altro esempio: la soluzione di x^3+3*x+1 = 0
pol <- function(x) 1+3*x+x^3
plot(pol,-3,3); abline(h=0,col="brown"); abline(v=0,col="brown")
 # si capisce che la soluzione è circa -3
polyroot(c(1,3,0,1))
[1] -0.3221854-0.000000i 0.1610927+1.754381i 0.1610927-1.754381i
# per memorizzare questi dati in variabili e/o esaminarne più cifre
# possiamo estrarre le parti reali e immaginarie con Re ed Im;
# vediamo come studiare la prima delle tre soluzioni
polyroot(c(1,3,0,1))[1]
[1] -0.3221854-0i
Re(polyroot(c(1,3,0,1))[1])
[1] -0.3221854
Re(polyroot(c(1,3,0,1))[1])+0.322185
[1] -3.546261e-07
Re(polyroot(c(1,3,0,1))[1])+0.32218535462
[1] -6.087575e-12
Re(polyroot(c(1,3,0,1))[1])+0.32218535462608757
[1] 0
# Questa soluzione (che è reale) avremmo potuto trovarla
# anche con i metodi discussi qui
#
# Una tabella: i valori per le durate di 5, 10, 15, …, 50 anni della
# crescita di 100 € secondo i tassi annuali di interesse composto,
# capitalizzato mensilmente, pari al 6%, all'8%, al 10% e al 12%.
# array indica una variabile indiciata (qui di 11 righe, 4 colonne)
# (una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2)
i <- c(6,8,10,12)/12/100
t <- array(dim=c(11,6)); k <- 0
for (a in seq(0,50,5)) { k <- k+1;
m <- a*12; t[k,1:6] <- c(a,m,round(100*(1+i)^m,2))}
t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 0 100.00 100.00 100.00 100.00
[2,] 5 60 134.89 148.98 164.53 181.67
[3,] 10 120 181.94 221.96 270.70 330.04
[4,] 15 180 245.41 330.69 445.39 599.58
[5,] 20 240 331.02 492.68 732.81 1089.26
[6,] 25 300 446.50 734.02 1205.69 1978.85
[7,] 30 360 602.26 1093.57 1983.74 3594.96
[8,] 35 420 812.36 1629.25 3263.87 6530.96
[9,] 40 480 1095.75 2427.34 5370.07 11864.77
[10,] 45 540 1478.00 3616.36 8835.42 21554.69
[11,] 50 600 1993.60 5387.82 14536.99 39158.34
#
# i sistemi lineari possono essere risolti rappresentandoli
# in forma matriciale. Ad es. x+3y=3 AND 2x+4y=7 lo rappresento con
# le matrici seguenti (gli elementi li introduco colonna per colonna):
ma <- matrix(data = c(1,2,3,4), nrow = 2, ncol = 2)
# Volendo introdurli riga per riga faccio:
ma <- matrix(data = c(1,3,2,4), nrow = 2, ncol = 2, byrow=TRUE)
# [una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2;
# usando array avrei dovuto scrivere:
# ma <- array(data = c(1,2,3,4), dim=c(2,2)) ]
ma
[,1] [,2]
[1,] 1 3
[2,] 2 4
# volendo la trasposta aziono:
t(ma)
[,1] [,2]
[1,] 1 2
[2,] 3 4
det(ma)
[1] -2
noti <- matrix(data = c(3,7), nrow = 2, ncol = 1)
noti
[,1]
[1,] 3
[2,] 7
solve(ma,noti)
[,1]
[1,] 4.5
[2,] -0.5
# facciamo la verifica:
1*4.5+3*-0.5; 2*4.5+4*-0.5
[1] 3
[1] 7
# ovvero, usando il prodotto tra matrici %*%:
sol <- solve(ma,noti); ma %*% sol
[,1]
[1,] 3
[2,] 7
# Altro esempio (inversa, m.identica)
#
# A righe e colonne (le "dimensioni" di una matrice) si possono dare nomi:
nomi <- list(c("proteine","grassi","glucidi"),c("pane","gamberetti","maionese"))
MA <- matrix(data=c(8,1,55,14,1,3,1,80,3), nrow=3, ncol=3, dimnames=nomi); MA
pane gamberetti maionese
proteine 8 14 1
grassi 1 1 80
glucidi 55 3 3
MA <- MA/100; MA # dalle percentuali ai rapporti:
pane gamberetti maionese
proteine 0.08 0.14 0.01
grassi 0.01 0.01 0.80
glucidi 0.55 0.03 0.03
#
# Qui come trovare risolvendo un sistema il cerchio per 3 punti dati
# si capisce che la soluzione è circa -3
polyroot(c(1,3,0,1))
[1] -0.3221854-0.000000i 0.1610927+1.754381i 0.1610927-1.754381i
# per memorizzare questi dati in variabili e/o esaminarne più cifre
# possiamo estrarre le parti reali e immaginarie con Re ed Im;
# vediamo come studiare la prima delle tre soluzioni
polyroot(c(1,3,0,1))[1]
[1] -0.3221854-0i
Re(polyroot(c(1,3,0,1))[1])
[1] -0.3221854
Re(polyroot(c(1,3,0,1))[1])+0.322185
[1] -3.546261e-07
Re(polyroot(c(1,3,0,1))[1])+0.32218535462
[1] -6.087575e-12
Re(polyroot(c(1,3,0,1))[1])+0.32218535462608757
[1] 0
# Questa soluzione (che è reale) avremmo potuto trovarla
# anche con i metodi discussi qui
#
# Una tabella: i valori per le durate di 5, 10, 15, …, 50 anni della
# crescita di 100 € secondo i tassi annuali di interesse composto,
# capitalizzato mensilmente, pari al 6%, all'8%, al 10% e al 12%.
# array indica una variabile indiciata (qui di 11 righe, 4 colonne)
# (una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2)
i <- c(6,8,10,12)/12/100
t <- array(dim=c(11,6)); k <- 0
for (a in seq(0,50,5)) { k <- k+1;
m <- a*12; t[k,1:6] <- c(a,m,round(100*(1+i)^m,2))}
t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 0 100.00 100.00 100.00 100.00
[2,] 5 60 134.89 148.98 164.53 181.67
[3,] 10 120 181.94 221.96 270.70 330.04
[4,] 15 180 245.41 330.69 445.39 599.58
[5,] 20 240 331.02 492.68 732.81 1089.26
[6,] 25 300 446.50 734.02 1205.69 1978.85
[7,] 30 360 602.26 1093.57 1983.74 3594.96
[8,] 35 420 812.36 1629.25 3263.87 6530.96
[9,] 40 480 1095.75 2427.34 5370.07 11864.77
[10,] 45 540 1478.00 3616.36 8835.42 21554.69
[11,] 50 600 1993.60 5387.82 14536.99 39158.34
#
# i sistemi lineari possono essere risolti rappresentandoli
# in forma matriciale. Ad es. x+3y=3 AND 2x+4y=7 lo rappresento con
# le matrici seguenti (gli elementi li introduco colonna per colonna):
ma <- matrix(data = c(1,2,3,4), nrow = 2, ncol = 2)
# Volendo introdurli riga per riga faccio:
ma <- matrix(data = c(1,3,2,4), nrow = 2, ncol = 2, byrow=TRUE)
# [una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2;
# usando array avrei dovuto scrivere:
# ma <- array(data = c(1,2,3,4), dim=c(2,2)) ]
ma
[,1] [,2]
[1,] 1 3
[2,] 2 4
# volendo la trasposta aziono:
t(ma)
[,1] [,2]
[1,] 1 2
[2,] 3 4
det(ma)
[1] -2
noti <- matrix(data = c(3,7), nrow = 2, ncol = 1)
noti
[,1]
[1,] 3
[2,] 7
solve(ma,noti)
[,1]
[1,] 4.5
[2,] -0.5
# facciamo la verifica:
1*4.5+3*-0.5; 2*4.5+4*-0.5
[1] 3
[1] 7
# ovvero, usando il prodotto tra matrici %*%:
sol <- solve(ma,noti); ma %*% sol
[,1]
[1,] 3
[2,] 7
# Altro esempio (inversa, m.identica)
#
# A righe e colonne (le "dimensioni" di una matrice) si possono dare nomi:
nomi <- list(c("proteine","grassi","glucidi"),c("pane","gamberetti","maionese"))
MA <- matrix(data=c(8,1,55,14,1,3,1,80,3), nrow=3, ncol=3, dimnames=nomi); MA
pane gamberetti maionese
proteine 8 14 1
grassi 1 1 80
glucidi 55 3 3
MA <- MA/100; MA # dalle percentuali ai rapporti:
pane gamberetti maionese
proteine 0.08 0.14 0.01
grassi 0.01 0.01 0.80
glucidi 0.55 0.03 0.03
#
# Qui come trovare risolvendo un sistema il cerchio per 3 punti dati
 # Con %*% posso calcolare anche il prodotto scalare (dot product) tra vettori
c(1,-2,2) %*% c(-4,0,2)
[,1]
[1,] 0
# i due vettori (1,-2,2) e (-4,0,2) sono quindi perpendicolari
# Per avere il prodotto scalare come numero usa drop
# drop( c(1,-2,2) %*% c(-4,0,2) )
[1] 0
# Per il prodotto vettoriale (cross product) posso fare:
prodv <- function(x,y) c(x[2]*y[3]-x[3]*y[2],x[3]*y[1]-x[1]*y[3],x[1]*y[2]-x[2]*y[1])
u <- c(0, 2.5, 1); v <- c(0, 2, 2)
prodv(u,v)
[1] 3 0 0
# Il modulo (distanza da O) di u, v e del vettore prodotto, e il versore di u:
dist <- function(P1,P2) sqrt(sum((P1-P2)^2))
dist(0,u); dist(0,v); dist(0, prodv(u,v) ); u/dist(0,u)
[1] 2.692582
[1] 2.828427
[1] 3
[1] 0.0000000 0.9284767 0.3713907
#
# Si possono calcolare facilmente le derivate di una funzione;
# [nota: R non calcola la derivata di abs(x), occore usare sqrt(x^2);
# vedi qui come derivare funzioni definite a tratti]
# ecco le derivate prima, seconda e terza di
# x -> x^2+x^3+sin(2*x)
D(expression(x^2+x^3+sin(2*x)),"x"); D(D(expression(x^2+x^3+sin(2*x)),"x"),"x")
D(D(D(expression(x^2+x^3+sin(2*x)), "x"),"x"),"x")
2 * x + 3 * x^2 + cos(2*x) * 2
2 + 3 * (2 * x) - sin(2*x) * 2 * 2
3 * 2 - cos(2 * x) * 2 * 2 * 2
# invece di expression si può usare quote
# (questi termini sono semplificabili facilmente a mano. Per
# semplificazioni più complesse posso usare WolframAlpha.com)
# Volendo posso definire la funzione e calcolare così le sue derivate
# (infatti body(f) è il termine con cui è stata definita f):
f <- function(x) x^2+x^3+sin(2*x)
D(body(f),"x"); D(D(body(f),"x"),"x"); D(D(D(body(f),"x"),"x"),"x")
# riottengo le stesse uscite.
# Ecco come definire le funzioni derivata, usando eval, che esprime
# il "valore" di un'espressione (in questo caso il valore che
# assume, al variare di x, un certo termine numerico)
g <- function(x) eval(D(body(f),"x"))
h <- function(x) eval(D(D(body(f),"x"),"x"))
k <- function(x) eval(D(D(D(body(f),"x"),"x"),"x"))
# ovvero: gx <- D(body(f),"x"); g <- function(x) eval(gx); ...
# I grafici della funzione e delle sue derivate:
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue")
curve(h,add=TRUE,col="green"); curve(k,add=TRUE,col="magenta")
# Con %*% posso calcolare anche il prodotto scalare (dot product) tra vettori
c(1,-2,2) %*% c(-4,0,2)
[,1]
[1,] 0
# i due vettori (1,-2,2) e (-4,0,2) sono quindi perpendicolari
# Per avere il prodotto scalare come numero usa drop
# drop( c(1,-2,2) %*% c(-4,0,2) )
[1] 0
# Per il prodotto vettoriale (cross product) posso fare:
prodv <- function(x,y) c(x[2]*y[3]-x[3]*y[2],x[3]*y[1]-x[1]*y[3],x[1]*y[2]-x[2]*y[1])
u <- c(0, 2.5, 1); v <- c(0, 2, 2)
prodv(u,v)
[1] 3 0 0
# Il modulo (distanza da O) di u, v e del vettore prodotto, e il versore di u:
dist <- function(P1,P2) sqrt(sum((P1-P2)^2))
dist(0,u); dist(0,v); dist(0, prodv(u,v) ); u/dist(0,u)
[1] 2.692582
[1] 2.828427
[1] 3
[1] 0.0000000 0.9284767 0.3713907
#
# Si possono calcolare facilmente le derivate di una funzione;
# [nota: R non calcola la derivata di abs(x), occore usare sqrt(x^2);
# vedi qui come derivare funzioni definite a tratti]
# ecco le derivate prima, seconda e terza di
# x -> x^2+x^3+sin(2*x)
D(expression(x^2+x^3+sin(2*x)),"x"); D(D(expression(x^2+x^3+sin(2*x)),"x"),"x")
D(D(D(expression(x^2+x^3+sin(2*x)), "x"),"x"),"x")
2 * x + 3 * x^2 + cos(2*x) * 2
2 + 3 * (2 * x) - sin(2*x) * 2 * 2
3 * 2 - cos(2 * x) * 2 * 2 * 2
# invece di expression si può usare quote
# (questi termini sono semplificabili facilmente a mano. Per
# semplificazioni più complesse posso usare WolframAlpha.com)
# Volendo posso definire la funzione e calcolare così le sue derivate
# (infatti body(f) è il termine con cui è stata definita f):
f <- function(x) x^2+x^3+sin(2*x)
D(body(f),"x"); D(D(body(f),"x"),"x"); D(D(D(body(f),"x"),"x"),"x")
# riottengo le stesse uscite.
# Ecco come definire le funzioni derivata, usando eval, che esprime
# il "valore" di un'espressione (in questo caso il valore che
# assume, al variare di x, un certo termine numerico)
g <- function(x) eval(D(body(f),"x"))
h <- function(x) eval(D(D(body(f),"x"),"x"))
k <- function(x) eval(D(D(D(body(f),"x"),"x"),"x"))
# ovvero: gx <- D(body(f),"x"); g <- function(x) eval(gx); ...
# I grafici della funzione e delle sue derivate:
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(f, add=TRUE,col="red"); curve(g, add=TRUE,col="blue")
curve(h,add=TRUE,col="green"); curve(k,add=TRUE,col="magenta")
 # Potrei rivare lo stesso grafico precedente con:
plot(f,-5,5,ylim=c(-30,30),col="red"); abline(v=0,h=0,col="brown")
plot(g,-5,5,add=TRUE,col="blue"); plot(h,-5,5,add=TRUE,col="green4")
plot(k,-5,5,add=TRUE,col="magenta")
# Ecco qui come ottenere un'animazione che traccia secanti e tangente
# ad una curva
# Potrei rivare lo stesso grafico precedente con:
plot(f,-5,5,ylim=c(-30,30),col="red"); abline(v=0,h=0,col="brown")
plot(g,-5,5,add=TRUE,col="blue"); plot(h,-5,5,add=TRUE,col="green4")
plot(k,-5,5,add=TRUE,col="magenta")
# Ecco qui come ottenere un'animazione che traccia secanti e tangente
# ad una curva
 # Se conosco il concetto di polonomio di Taylor, posso approssimare f con
# una funzione polinomiale. Ecco quella di grado 3 (per g,h,k vedi sopra):
# [ vedi qui per una sintesi ]
p <- function(x) f(0)+g(0)*x+h(0)*x^2/factorial(2)+k(0)*x^3/factorial(3)
# e il suo grafico aggiunto a quello di f
plot(p,-5,5,add=TRUE)
# Se conosco il concetto di polonomio di Taylor, posso approssimare f con
# una funzione polinomiale. Ecco quella di grado 3 (per g,h,k vedi sopra):
# [ vedi qui per una sintesi ]
p <- function(x) f(0)+g(0)*x+h(0)*x^2/factorial(2)+k(0)*x^3/factorial(3)
# e il suo grafico aggiunto a quello di f
plot(p,-5,5,add=TRUE)
 #
# in R .Last.value consente di richiamare l'ultima uscita; ecco
# come si potrebbe usare per calcoli come i precedenti:
fun <- function(x) x^4+x^3; D(body(fun),"x")
4 * x^3 + 3 * x^2
D(.Last.value,"x")
4 * (3 * x^2) + 3 * (2 * x)
D(.Last.value,"x")
4 * (3 * (2 * x)) + 3 * 2
D(.Last.value,"x")
4 * (3 * 2)
D(.Last.value,"x")
[1] 0
#
# Ovviamente, è facile determinare punti di minimo/massimo/flesso
# di funzioni di cui si conosce l'espressione analitica: un esempio;
# una animazione.
#
# in R .Last.value consente di richiamare l'ultima uscita; ecco
# come si potrebbe usare per calcoli come i precedenti:
fun <- function(x) x^4+x^3; D(body(fun),"x")
4 * x^3 + 3 * x^2
D(.Last.value,"x")
4 * (3 * x^2) + 3 * (2 * x)
D(.Last.value,"x")
4 * (3 * (2 * x)) + 3 * 2
D(.Last.value,"x")
4 * (3 * 2)
D(.Last.value,"x")
[1] 0
#
# Ovviamente, è facile determinare punti di minimo/massimo/flesso
# di funzioni di cui si conosce l'espressione analitica: un esempio;
# una animazione.
 # (metodi che non impiegano la derivazione sono illustrati qui)
#
# Come ottenere il grafico di una funzione e quello della sua
# derivata in due finestre diverse:
dev.new(width=4,height=4)
view <- c(-3,3, -1,10); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-1,10,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
f <- function(x) x^2
plot(f,view[1],view[2],add=TRUE,col="blue")
dev.new(width=4,height=4)
view <- c(-3,3, -6,6); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-6,6,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
gx <-D(body(f),"x"); g <- function(x) eval(gx)
plot(g,view[1],view[2],add=TRUE,col="blue")
# (metodi che non impiegano la derivazione sono illustrati qui)
#
# Come ottenere il grafico di una funzione e quello della sua
# derivata in due finestre diverse:
dev.new(width=4,height=4)
view <- c(-3,3, -1,10); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-1,10,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
f <- function(x) x^2
plot(f,view[1],view[2],add=TRUE,col="blue")
dev.new(width=4,height=4)
view <- c(-3,3, -6,6); orig <- c(0,0)
tx<- seq(-3,3,1); ty<- seq(-6,6,1)
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="")
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
arrows(view[1],orig[2],view[2]+(view[2]-view[1])/30,orig[2],length=0.1,col="brown")
arrows(orig[1],view[3],orig[1],view[4]+(view[4]-view[3])/30,length=0.1,col="brown")
gx <-D(body(f),"x"); g <- function(x) eval(gx)
plot(g,view[1],view[2],add=TRUE,col="blue")
 #
# il calcolo di integrali definiti:
t <- function(x) 3*x^2+1; integrate(t,0,1); integrate(t,-1,1)
2 with absolute error < 2.2e-14
4 with absolute error < 4.4e-14
# Se vuoi avere solo il valore aggiungi $value
integrate(t,-1,1)$value
[1] 4
# Ma si possono ottenere facilmente con un programmino: vedi qui o qui
#
# Posso migliorare la precisione relativa del calcolo con rel.tol. Es.:
F <- function(x) sin(x^3)+exp(x)
integrate(F, -5,10)
22027.3 with absolute error < 2.6
integrate(F, -5,10,rel.tol=1e-6)
22026.47 with absolute error < 0.018
print(integrate(F, -5,10,rel.tol=1e-8),16)
22026.46763874626 with absolute error < 6.9e-05
#
# Per il grafico della funzione integrale tra 0 ed x di g posso
# caricare i comandi (area) contenuti nella libreria MASS (ma
# funziona bene solo in casi semplici; per altri casi vedi sotto)
library(MASS)
g <- function(x) 2 * x + 3 * x^2 + cos(x)
k <- function(x) area(g,0,x)
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(g, add=TRUE,col="blue")
curve(k, add=TRUE,col="green")
#
# il calcolo di integrali definiti:
t <- function(x) 3*x^2+1; integrate(t,0,1); integrate(t,-1,1)
2 with absolute error < 2.2e-14
4 with absolute error < 4.4e-14
# Se vuoi avere solo il valore aggiungi $value
integrate(t,-1,1)$value
[1] 4
# Ma si possono ottenere facilmente con un programmino: vedi qui o qui
#
# Posso migliorare la precisione relativa del calcolo con rel.tol. Es.:
F <- function(x) sin(x^3)+exp(x)
integrate(F, -5,10)
22027.3 with absolute error < 2.6
integrate(F, -5,10,rel.tol=1e-6)
22026.47 with absolute error < 0.018
print(integrate(F, -5,10,rel.tol=1e-8),16)
22026.46763874626 with absolute error < 6.9e-05
#
# Per il grafico della funzione integrale tra 0 ed x di g posso
# caricare i comandi (area) contenuti nella libreria MASS (ma
# funziona bene solo in casi semplici; per altri casi vedi sotto)
library(MASS)
g <- function(x) 2 * x + 3 * x^2 + cos(x)
k <- function(x) area(g,0,x)
x1 <- -5; x2 <- 5; y1 <- -30; y2 <- 30
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
abline(h=0,col="brown"); abline(v=0,col="brown")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(g, add=TRUE,col="blue")
curve(k, add=TRUE,col="green")
 # Usando la funzione "area" è possibile avere direttamente il valore
# di un integrale su un intervallo finito (usa metodi approssimati come
# "integrate" ma non visualizza l'errore):
area(t,0,1); area(t,-1,1)
[1] 2
[1] 4
# Per il graf. della funz. integrale posso anche usare integrate e
# procedere per punti:
a <- -5; b <- 5; x0 <- 0; n <- 5000
for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(g,x0,x)$value,pch=".",col="red") }
#
# Le primitive di una "funzione elementare" non sono sempre funzioni
# elementari, per cui non c'e' modo di avere l'integrale indefinito
# di una qualunque funzione in forma simbolica (in molti casi tuttavia
# posso ricorrere ad es. a WolframAlpha.com). Posso però definire
# definire metodi di calcolo per particolari funzioni. Vediamo come
# farlo per le funzioni polinomiali.
# Mettiamo i coeff. del polinomio a partire dal grado 0
Q <- c(-2,-3,2.4,-1/5) # il pol. -2-3*x+2.4*x^2-1/5*x^3
int <- function(p) { inte <- 0;
for (i in 1:length(p)) inte <- c(inte,p[i]/i); inte}
int(Q)
[1] 0.00 -2.00 -1.50 0.80 -0.05
library(MASS); fractions(int(Q))
[1] 0 -2 -3/2 4/5 -1/20
# Le primitive sono x -> c-2*x-3/2*x^2+4/5*x^3-x^4/20
# Volendo i grafici:
f <- function(x) Q[1]+x*Q[2]+x^2*Q[3]+x^3*Q[4]
plot(f,-3,12,ylim=c(-10,150)); abline(h=0,v=0,lty=3)
g <- function(x) c-2*x-3/2*x^2+4/5*x^3-x^4/20
for(c in (-7:10)*20) plot(g,-3,12,add=TRUE,col="red",lty=3)
# Usando la funzione "area" è possibile avere direttamente il valore
# di un integrale su un intervallo finito (usa metodi approssimati come
# "integrate" ma non visualizza l'errore):
area(t,0,1); area(t,-1,1)
[1] 2
[1] 4
# Per il graf. della funz. integrale posso anche usare integrate e
# procedere per punti:
a <- -5; b <- 5; x0 <- 0; n <- 5000
for(i in 0:n) {x <- a+(b-a)/n*i; points(x,integrate(g,x0,x)$value,pch=".",col="red") }
#
# Le primitive di una "funzione elementare" non sono sempre funzioni
# elementari, per cui non c'e' modo di avere l'integrale indefinito
# di una qualunque funzione in forma simbolica (in molti casi tuttavia
# posso ricorrere ad es. a WolframAlpha.com). Posso però definire
# definire metodi di calcolo per particolari funzioni. Vediamo come
# farlo per le funzioni polinomiali.
# Mettiamo i coeff. del polinomio a partire dal grado 0
Q <- c(-2,-3,2.4,-1/5) # il pol. -2-3*x+2.4*x^2-1/5*x^3
int <- function(p) { inte <- 0;
for (i in 1:length(p)) inte <- c(inte,p[i]/i); inte}
int(Q)
[1] 0.00 -2.00 -1.50 0.80 -0.05
library(MASS); fractions(int(Q))
[1] 0 -2 -3/2 4/5 -1/20
# Le primitive sono x -> c-2*x-3/2*x^2+4/5*x^3-x^4/20
# Volendo i grafici:
f <- function(x) Q[1]+x*Q[2]+x^2*Q[3]+x^3*Q[4]
plot(f,-3,12,ylim=c(-10,150)); abline(h=0,v=0,lty=3)
g <- function(x) c-2*x-3/2*x^2+4/5*x^3-x^4/20
for(c in (-7:10)*20) plot(g,-3,12,add=TRUE,col="red",lty=3)
 # Sono stati evidenziati anche zeri/punti di max/min di f/g:
polyroot(Q)
[1] -0.4772256+0i 2.0000000-0i 10.4772256+0i
abline(v=c(-0.4772256,2.0000000,10.4772256),lty=2,col="blue")
#
# Vedi qui come affrontare, più in generale, lo studio delle
# equazioni differenziali del 1º ordine, e tracciare il campo direzionale.
# Vedi qui per studiare quelle del 2º ordine e tracciarne il diagramma di fase
#
# il simbolo Inf rappresenta l'infinito
# NOTA: come abbiamo visto viene assunto il "valore" Inf quando un numero
# eccede un certo valore. Analogamente viene assunto il valore 0 quando il
# valore assoluto di un numero è molto piccolo. Per dettagli aziona:
.Machine
#
h <- function(x) exp(-x)
x1 <- -1; x2 <- 10; y1 <- -1/10; y2 <- 1
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(h, add=TRUE, col="blue")
# Sono stati evidenziati anche zeri/punti di max/min di f/g:
polyroot(Q)
[1] -0.4772256+0i 2.0000000-0i 10.4772256+0i
abline(v=c(-0.4772256,2.0000000,10.4772256),lty=2,col="blue")
#
# Vedi qui come affrontare, più in generale, lo studio delle
# equazioni differenziali del 1º ordine, e tracciare il campo direzionale.
# Vedi qui per studiare quelle del 2º ordine e tracciarne il diagramma di fase
#
# il simbolo Inf rappresenta l'infinito
# NOTA: come abbiamo visto viene assunto il "valore" Inf quando un numero
# eccede un certo valore. Analogamente viene assunto il valore 0 quando il
# valore assoluto di un numero è molto piccolo. Per dettagli aziona:
.Machine
#
h <- function(x) exp(-x)
x1 <- -1; x2 <- 10; y1 <- -1/10; y2 <- 1
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
curve(h, add=TRUE, col="blue")
 integrate(h,0,Inf)
1 with absolute error < 5.7e-05
# per avere l'uscita numerica senza la precisone basta usare $value:
integrate(h,0,Inf)$value
[1] 1
# il limite per x -> Inf di h è 0:
h(1); h(10); h(100); h(Inf)
[1] 0.3678794
[1] 4.539993e-05
[1] 3.720076e-44
[1] 0
# nota: la funzione "area" è usabile solo per calcolare integrali
# su intervalli finiti: area(h,0,Inf) segnalerebbe "errore"
#
# Attenzione: il limite di f(x) per x -> Inf è stimabile con f(Inf) non in
# tutti i casi. È beve valutare f(x) per x che cresce per controllare. Es.:
f <- function(x) (1+1/x)^x; f(Inf)
[1] 1
# mentre il limite è e:
n <- 1:8; f(10^n)
[1] 2.593742 2.704814 2.716924 2.718146 2.718268 2.718280 2.718282 2.718282
#
# i limiti di q(x) per q che tende ad 1 da destra e da sinistra sono diversi
q <- function(x) (x^2-1)/(x^2-2*x+1); plot(q,-2,2)
integrate(h,0,Inf)
1 with absolute error < 5.7e-05
# per avere l'uscita numerica senza la precisone basta usare $value:
integrate(h,0,Inf)$value
[1] 1
# il limite per x -> Inf di h è 0:
h(1); h(10); h(100); h(Inf)
[1] 0.3678794
[1] 4.539993e-05
[1] 3.720076e-44
[1] 0
# nota: la funzione "area" è usabile solo per calcolare integrali
# su intervalli finiti: area(h,0,Inf) segnalerebbe "errore"
#
# Attenzione: il limite di f(x) per x -> Inf è stimabile con f(Inf) non in
# tutti i casi. È beve valutare f(x) per x che cresce per controllare. Es.:
f <- function(x) (1+1/x)^x; f(Inf)
[1] 1
# mentre il limite è e:
n <- 1:8; f(10^n)
[1] 2.593742 2.704814 2.716924 2.718146 2.718268 2.718280 2.718282 2.718282
#
# i limiti di q(x) per q che tende ad 1 da destra e da sinistra sono diversi
q <- function(x) (x^2-1)/(x^2-2*x+1); plot(q,-2,2)
 q(1-1E-2);q(1-1E-5);q(1-1E-10)
[1] -199
[1] -199999
[1] -Inf
q(1+1E-2);q(1+1E-5);q(1+1E-10)
[1] 201
[1] 200001
[1] Inf
#
# Un altro esempio. Lo studio, data una funzione f, dei punti di flesso
# che assume in [0,5] la sua primitiva F avente valore 0 in 0. Qui i
# valori sono trovati arrotondati ai centesimi (sono tracciate in verde
# scuro le rette verticali che li hanno come ascissa: vedi l'ultimo
# comando "abline").
f <- function(x) x+sin(x)^4*cos(x)^5*60
a <- 0; b <- 5
plot(f,a,b,ylim=c(-7,10)); abline(h=0)
abline(v=c(0,1,2,3,4,5),lty=3,col="grey")
fx <- body(f)
Dfx <-D(fx,"x"); Df <- function(x) eval(Dfx)
plot(Df,a,b,add=TRUE,col="blue")
If <- function(x) integrate(f,0,x)$value
for(i in 0:1000){x<-a+(b-a)/1000*i;points(x,If(x),pch=".",col="red")}
abline(v=c(0.75,1.32,1.83,2.39,3.31,3.85),lty=3,col="green4")
q(1-1E-2);q(1-1E-5);q(1-1E-10)
[1] -199
[1] -199999
[1] -Inf
q(1+1E-2);q(1+1E-5);q(1+1E-10)
[1] 201
[1] 200001
[1] Inf
#
# Un altro esempio. Lo studio, data una funzione f, dei punti di flesso
# che assume in [0,5] la sua primitiva F avente valore 0 in 0. Qui i
# valori sono trovati arrotondati ai centesimi (sono tracciate in verde
# scuro le rette verticali che li hanno come ascissa: vedi l'ultimo
# comando "abline").
f <- function(x) x+sin(x)^4*cos(x)^5*60
a <- 0; b <- 5
plot(f,a,b,ylim=c(-7,10)); abline(h=0)
abline(v=c(0,1,2,3,4,5),lty=3,col="grey")
fx <- body(f)
Dfx <-D(fx,"x"); Df <- function(x) eval(Dfx)
plot(Df,a,b,add=TRUE,col="blue")
If <- function(x) integrate(f,0,x)$value
for(i in 0:1000){x<-a+(b-a)/1000*i;points(x,If(x),pch=".",col="red")}
abline(v=c(0.75,1.32,1.83,2.39,3.31,3.85),lty=3,col="green4")
 #
# Lo studio di una serie: 1-1/2+1/3-1/4+1/5...
a <- function(n) (-1)^(n+1)/n # a(n) elemento n-esimo della sommatoria
N <- function(n) seq(1,n,1) # N = 1 2 ... n
S <- function(n) sum(a(N(n))) # somma a(1)+...a(n)
NMax <- 20; y1 <- 0; y2 <- 1 # parte di piano che scelgo
plot(c(0,NMax),c(y1,y2),type="n",xlab="", ylab="")
for(i in 1:NMax) points(i,S(i),pch=".", cex=3)
for(i in 1:(NMax-1)) lines(c(i,i+1),c(S(i),S(i+1)),lty=3)
#
# Lo studio di una serie: 1-1/2+1/3-1/4+1/5...
a <- function(n) (-1)^(n+1)/n # a(n) elemento n-esimo della sommatoria
N <- function(n) seq(1,n,1) # N = 1 2 ... n
S <- function(n) sum(a(N(n))) # somma a(1)+...a(n)
NMax <- 20; y1 <- 0; y2 <- 1 # parte di piano che scelgo
plot(c(0,NMax),c(y1,y2),type="n",xlab="", ylab="")
for(i in 1:NMax) points(i,S(i),pch=".", cex=3)
for(i in 1:(NMax-1)) lines(c(i,i+1),c(S(i),S(i+1)),lty=3)
 # stampo i valori della sommatoria e del termine successivo
# che verrebbe sommato
n <- 100; S(n);a(n+1)
# 0.6881722 0.00990099
n <- 1e3; S(n);a(n+1)
# ...
n <- 1e7; S(n);a(n+1)
# 0.6931471 1e-07
library(codetools); showTree(log(2))
# 0.693147180559945
#
# È facilmente realizzabile lo studio di serie di Fourier
# (esitono anche specifici comandi per studiarle). Un esempio:
p <- function(x) {f <- 0;
for(i in 0:n) f <- f+sin((2*i+1)*x)/(2*i+1); f <- f*4/pi}
n <- 1; plot(p,-5,10, col="blue",n=1000)
abline(h=0,v=0,lty=2,col="blue")
abline(v=axTicks(1), h=axTicks(2), col="grey",lty=3)
n <- 2; plot(p,-5,10,add=TRUE,col="red",n=1000)
n <- 3; plot(p,-5,10,add=TRUE,col="green",n=1000)
n <- 1000; plot(p,-5,10,add=TRUE,col="brown",n=5000)
# stampo i valori della sommatoria e del termine successivo
# che verrebbe sommato
n <- 100; S(n);a(n+1)
# 0.6881722 0.00990099
n <- 1e3; S(n);a(n+1)
# ...
n <- 1e7; S(n);a(n+1)
# 0.6931471 1e-07
library(codetools); showTree(log(2))
# 0.693147180559945
#
# È facilmente realizzabile lo studio di serie di Fourier
# (esitono anche specifici comandi per studiarle). Un esempio:
p <- function(x) {f <- 0;
for(i in 0:n) f <- f+sin((2*i+1)*x)/(2*i+1); f <- f*4/pi}
n <- 1; plot(p,-5,10, col="blue",n=1000)
abline(h=0,v=0,lty=2,col="blue")
abline(v=axTicks(1), h=axTicks(2), col="grey",lty=3)
n <- 2; plot(p,-5,10,add=TRUE,col="red",n=1000)
n <- 3; plot(p,-5,10,add=TRUE,col="green",n=1000)
n <- 1000; plot(p,-5,10,add=TRUE,col="brown",n=5000)
 # Per n=1000 ci si avvicina alla "somma", volendo tracciabile con i
# comandi seguenti ( quad(x) riconduce x a [-pi,pi) )
quad <- function(x) {y <- floor(x/(2*pi)); y <- x-y*2*pi;
y <- y-2*pi*ifelse(y >= pi,1,0); y }
F <- function(x) {x <- quad(x);
ifelse(0 < x & x < pi,1,ifelse(-pi < x & x <0,-1,0))}
plot(F,-5,10,add=TRUE,n=1000,col="grey50")
#
# grafico di una funzione di 2 variabili (x,y)-> sin(x)+cos(2y)
# theta, phi e d indicano la posizione dell'occhio: la direzione dello
# sguardo proiettata sul piano orizzontale, la sua inclinazione rispetto
# a tale piano e la distanza dell'occhio dal centro del box. La figura
# seguente figura illustra il significato di theta e di phi:
# Per n=1000 ci si avvicina alla "somma", volendo tracciabile con i
# comandi seguenti ( quad(x) riconduce x a [-pi,pi) )
quad <- function(x) {y <- floor(x/(2*pi)); y <- x-y*2*pi;
y <- y-2*pi*ifelse(y >= pi,1,0); y }
F <- function(x) {x <- quad(x);
ifelse(0 < x & x < pi,1,ifelse(-pi < x & x <0,-1,0))}
plot(F,-5,10,add=TRUE,n=1000,col="grey50")
#
# grafico di una funzione di 2 variabili (x,y)-> sin(x)+cos(2y)
# theta, phi e d indicano la posizione dell'occhio: la direzione dello
# sguardo proiettata sul piano orizzontale, la sua inclinazione rispetto
# a tale piano e la distanza dell'occhio dal centro del box. La figura
# seguente figura illustra il significato di theta e di phi:
 x <- y <- seq(-pi,pi, by=0.2)
f <- function(x,y) sin(x)+cos(2*y)
z <- outer(x,y,f) # crea la matrice z delle altezze
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed")
# a destra il grafico "non colorato"
persp(x,y,z,phi=60,theta=30,d=20,col=NULL,ticktype="detailed")
x <- y <- seq(-pi,pi, by=0.2)
f <- function(x,y) sin(x)+cos(2*y)
z <- outer(x,y,f) # crea la matrice z delle altezze
persp(x,y,z,phi=60,theta=30,d=20,col="yellow",ticktype="detailed")
# a destra il grafico "non colorato"
persp(x,y,z,phi=60,theta=30,d=20,col=NULL,ticktype="detailed")
 # cosa si otterrebbe con d=1 e (theta,phi) pari a (0,0), (0,90), (90,0):
# cosa si otterrebbe con d=1 e (theta,phi) pari a (0,0), (0,90), (90,0):
 # e le curve di livello
contour(x,y,z)
# e le curve di livello
contour(x,y,z)
 contour(x,y,z,col=heat.colors(12))
contour(x,y,z,zlim=c(0,2))
contour(x,y,z,zlim=c(0,-2))
contour(x,y,z,col=heat.colors(12),nlevels=5)
contour(x,y,z,zlim=c(0,2),nlevels=5)
contour(x,y,z, levels=c(-1,0,0.5,1) )
contour(x,y,z,col=heat.colors(12))
contour(x,y,z,zlim=c(0,2))
contour(x,y,z,zlim=c(0,-2))
contour(x,y,z,col=heat.colors(12),nlevels=5)
contour(x,y,z,zlim=c(0,2),nlevels=5)
contour(x,y,z, levels=c(-1,0,0.5,1) )
 # Altri modi di visulizzare le curve di livello:
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=heat.colors(5) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(3) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(5) )
# Un esempi commentati dettagliatamente li trovi qui e qui
# Altri modi di visulizzare le curve di livello:
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=heat.colors(5) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(3) )
contour(x,y,z, levels=c(-1,-1/2,0,1/2,1), col=rainbow(5) )
# Un esempi commentati dettagliatamente li trovi qui e qui
 # un altro esempio:
x <- y <- seq(-10, 10, len = 30)
f <- function(x,y) { r <- sqrt(x^2+y^2); 10 * sin(r)/r }
z <- outer(x, y, f)
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
# Volendo posso ridurre i margini (e quindi ingrandire la figura) azionando
# prima: par( mai = c(0.3,0.3,0.3,0.3) ) (vedi)
# un altro esempio:
x <- y <- seq(-10, 10, len = 30)
f <- function(x,y) { r <- sqrt(x^2+y^2); 10 * sin(r)/r }
z <- outer(x, y, f)
persp(x, y, z, theta = 30, phi = 30, expand = 0.5, col = "lightblue")
# Volendo posso ridurre i margini (e quindi ingrandire la figura) azionando
# prima: par( mai = c(0.3,0.3,0.3,0.3) ) (vedi)
 # ottengo la prima figura; la seconda è stata ottenuta aggiungendo le ombre:
persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue", shade=0.4)
# Azionando expand posso modificare i rapporti tra le scale:
persp(x,y,z, theta=30, phi=30, expand=0.25, col="lightblue", shade=0.4)
# ottengo la prima figura; la seconda è stata ottenuta aggiungendo le ombre:
persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue", shade=0.4)
# Azionando expand posso modificare i rapporti tra le scale:
persp(x,y,z, theta=30, phi=30, expand=0.25, col="lightblue", shade=0.4)
 # Usando trans3d() aggiungo dei pezzi, ottenendo la figura a sinistra
# Usando trans3d() aggiungo dei pezzi, ottenendo la figura a sinistra
 fig <- persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue")
xE <- c(-10,10); xy <- expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = fig), col = 2, pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = fig), col = 3)
# con altri comandi ottengo la figura a destra:
phi <- seq(0, 2*pi, len = 201)
r1 <- 7.725 # raggio del "secondo" massimo
xr <- r1 * cos(phi)
yr <- r1 * sin(phi)
lines(trans3d(xr,yr, f(xr,yr), fig), col = "brown", lwd = 2)
# si è fatto un altro uso di seq
seq(-10, 10, len = 30)
[1] -10.0000000 -9.3103448 -8.6206897 -7.9310345 -7.2413793
[6] -6.5517241 -5.8620690 -5.1724138 -4.4827586 -3.7931034
[11] -3.1034483 -2.4137931 -1.7241379 -1.0344828 -0.3448276
[16] 0.3448276 1.0344828 1.7241379 2.4137931 3.1034483
[21] 3.7931034 4.4827586 5.1724138 5.8620690 6.5517241
[26] 7.2413793 7.9310345 8.6206897 9.3103448 10.0000000
#
# Per il calcolo di gradiente ed hessiano cerca fdHess nell'help di R
# Qui trovi un esempio in cui il gradiente e l'hessiano sono costruiti.
#
# Un'altra figura tridimensionale (xlim,… -vedi- indica l'intervallo per le x,...)
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
persp(x,y,z,theta=-20,phi=25,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
fig <- persp(x,y,z, theta=30, phi=30, expand=0.5, col="lightblue")
xE <- c(-10,10); xy <- expand.grid(xE, xE)
points(trans3d(xy[,1], xy[,2], 6, pmat = fig), col = 2, pch =16)
lines (trans3d(x, y=10, z= 6 + sin(x), pmat = fig), col = 3)
# con altri comandi ottengo la figura a destra:
phi <- seq(0, 2*pi, len = 201)
r1 <- 7.725 # raggio del "secondo" massimo
xr <- r1 * cos(phi)
yr <- r1 * sin(phi)
lines(trans3d(xr,yr, f(xr,yr), fig), col = "brown", lwd = 2)
# si è fatto un altro uso di seq
seq(-10, 10, len = 30)
[1] -10.0000000 -9.3103448 -8.6206897 -7.9310345 -7.2413793
[6] -6.5517241 -5.8620690 -5.1724138 -4.4827586 -3.7931034
[11] -3.1034483 -2.4137931 -1.7241379 -1.0344828 -0.3448276
[16] 0.3448276 1.0344828 1.7241379 2.4137931 3.1034483
[21] 3.7931034 4.4827586 5.1724138 5.8620690 6.5517241
[26] 7.2413793 7.9310345 8.6206897 9.3103448 10.0000000
#
# Per il calcolo di gradiente ed hessiano cerca fdHess nell'help di R
# Qui trovi un esempio in cui il gradiente e l'hessiano sono costruiti.
#
# Un'altra figura tridimensionale (xlim,… -vedi- indica l'intervallo per le x,...)
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
persp(x,y,z,theta=-20,phi=25,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
 # la prima e altre due visioni
persp(x,y,z,theta=-45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
persp(x,y,z,theta=45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
# Con l'opzione scale=TRUE, omettibile, la figura è tracciata adattando le
# scale sui vari assi. Invece con scale=FALSE essa non viene diversamente
# scalata (si ha un sistema monometrico). Aggiungendo ticktype="detailed"
# vengono visulizzate delle tacche che consentono di capire il fenomeno.
persp(x,y,z,theta=45,phi=25,col="grey",zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
persp(x,y,z,theta=45,phi=25,col="grey",scale=FALSE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
# la prima e altre due visioni
persp(x,y,z,theta=-45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
persp(x,y,z,theta=45,phi=45,col="grey",scale=TRUE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4))
# Con l'opzione scale=TRUE, omettibile, la figura è tracciata adattando le
# scale sui vari assi. Invece con scale=FALSE essa non viene diversamente
# scalata (si ha un sistema monometrico). Aggiungendo ticktype="detailed"
# vengono visulizzate delle tacche che consentono di capire il fenomeno.
persp(x,y,z,theta=45,phi=25,col="grey",zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
persp(x,y,z,theta=45,phi=25,col="grey",scale=FALSE,zlim=c(0,15),xlim=c(0,4),ylim=c(0,4),ticktype="detailed")
 # L'immagine sotto (in scala monometrica) è ottenuta aggiungendo un punto e
# una spezzata, usando trans3d per darne le coordinate; per fare l'aggiunta occorre
# memorizzare la prima figura (qui l'abbiamo chiamata A) e poi richiamarla con pmat:
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
zlim=c(0,15),xlim=c(-1,10),ylim=c(-1,10), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
# L'immagine sotto (in scala monometrica) è ottenuta aggiungendo un punto e
# una spezzata, usando trans3d per darne le coordinate; per fare l'aggiunta occorre
# memorizzare la prima figura (qui l'abbiamo chiamata A) e poi richiamarla con pmat:
x <- c(1,2,3,4); y <- c(1,2,3)
z <- c(0, 3,13,11,
12, 5,11,10,
10,11, 5, 0)
z <- array(z,dim=c(4,3))
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
zlim=c(0,15),xlim=c(-1,10),ylim=c(-1,10), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
 # Sopra a destra l'immagine riducendo con nticks il numero delle tacche:
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
nticks=3,zlim=c(0,15),xlim=c(-1,11),ylim=c(-1,11), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
#
# Un altro esempio (vedi qui o qui, o qui): una casetta (fatta pezzo
# per pezzo) e i "punti all'infinito"
# Sopra a destra l'immagine riducendo con nticks il numero delle tacche:
A <- persp(x,y,z, theta=130,phi=20,col="grey", ticktype="detailed",
nticks=3,zlim=c(0,15),xlim=c(-1,11),ylim=c(-1,11), scale=FALSE)
points(trans3d(x=2,y=2,z=12,pmat=A), col = 2, pch =16)
lines(trans3d(x=c(2,9,5),y=c(2,0,10),z=c(12,0,5),pmat=A), col=4)
#
# Un altro esempio (vedi qui o qui, o qui): una casetta (fatta pezzo
# per pezzo) e i "punti all'infinito"


 # Altro esempio con spiegazioni dettagliate
#
# Una curva nello spazio (5 giri di un'elica)
t <- seq(0,10*pi,len=1000)
z0 <- c(0,10*pi); u <- rep(z0[1],4) # metto in u la base del box
z <- array(u,dim=c(2,2)); x <- c(-2,2); y <- c(-2,2)
F <- persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# per averla senza box avrei aggiunto in persp: border="white",box=FALSE)
# Altro esempio con spiegazioni dettagliate
#
# Una curva nello spazio (5 giri di un'elica)
t <- seq(0,10*pi,len=1000)
z0 <- c(0,10*pi); u <- rep(z0[1],4) # metto in u la base del box
z <- array(u,dim=c(2,2)); x <- c(-2,2); y <- c(-2,2)
F <- persp(x,y,z,theta=30,phi=20,scale=TRUE,zlim=z0,xlim=x,ylim=y,d=1)
lines(trans3d(cos(t),sin(t),t,pmat=F),col="red")
# per averla senza box avrei aggiunto in persp: border="white",box=FALSE)


 # Sopra al centro un'altra figura (qui) e a destra un'altra (qui)
#
# Sotto a sinistra la terra e la rotta longitudine=latitudine (vedi).
# Un'ulteriore figura (volcano), a destra, già memorizzata nel programma
z <- 3 * volcano # moltiplico per 3 i dati
y <- 10 * (1:ncol(z)) # 10 meter spacing (E to W)
x <- 10 * (1:nrow(z)) # 10 meter spacing (S to N)
par(bg = "grey")
persp(x,y,z,theta=135,phi=30,col="green3",scale=FALSE,ltheta=-120,shade=0.75,border=NA,box=FALSE)
# Sopra al centro un'altra figura (qui) e a destra un'altra (qui)
#
# Sotto a sinistra la terra e la rotta longitudine=latitudine (vedi).
# Un'ulteriore figura (volcano), a destra, già memorizzata nel programma
z <- 3 * volcano # moltiplico per 3 i dati
y <- 10 * (1:ncol(z)) # 10 meter spacing (E to W)
x <- 10 * (1:nrow(z)) # 10 meter spacing (S to N)
par(bg = "grey")
persp(x,y,z,theta=135,phi=30,col="green3",scale=FALSE,ltheta=-120,shade=0.75,border=NA,box=FALSE)

 # la "corretta" rappresentazione prospettica consente significative
# attività matematiche; un esempio:
# una parabola che sembra un'ellisse (lo spazio è [0,10]*[0,10]*[0,10]):
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=FALSE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# la "corretta" rappresentazione prospettica consente significative
# attività matematiche; un esempio:
# una parabola che sembra un'ellisse (lo spazio è [0,10]*[0,10]*[0,10]):
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=FALSE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
 x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=TRUE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# visione con phi=5; ecco che cosa si ottiene con phi=45 e con phi=60:
x <- c(0,10); y <- c(0,10); z <- array(c(0,0,0,0),dim=c(2,2))
pr<- persp(x,y,z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",ylab="y",zlab="z",box=TRUE,border="grey",phi=5,theta=-30)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
# visione con phi=5; ecco che cosa si ottiene con phi=45 e con phi=60:
 # proc.time() fornisce l'ora (dall'avvio del programma), con [3] i secondi
# Per avere data ed ora occorre invece usare date() (si ha una uscita
# come: "Mon Dec 19 17:55:38 2011" ). Per altri modi per avere l'ora vedi
# (qui trovi anche come trasformare un numero tra virgolette in un numero).
# Ecco un contasecondi. Per arrestarlo premi il tasto ESC. In modo analogo
# si possono creare animazioni dei più vari tipi.
# tic(x) fa passare x sec; plot(...) prepara lo schermo; la 3^a e' l'orologio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec}
plot(c(0,1),c(0,1),xlab="", ylab="", col="white", col.axis="white"); i<-0
while(1<2){rect(0,0,1,1,col="yellow"); text(0.5,0.1,i); tic(1); i<-i+1}
# proc.time() fornisce l'ora (dall'avvio del programma), con [3] i secondi
# Per avere data ed ora occorre invece usare date() (si ha una uscita
# come: "Mon Dec 19 17:55:38 2011" ). Per altri modi per avere l'ora vedi
# (qui trovi anche come trasformare un numero tra virgolette in un numero).
# Ecco un contasecondi. Per arrestarlo premi il tasto ESC. In modo analogo
# si possono creare animazioni dei più vari tipi.
# tic(x) fa passare x sec; plot(...) prepara lo schermo; la 3^a e' l'orologio
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec}
plot(c(0,1),c(0,1),xlab="", ylab="", col="white", col.axis="white"); i<-0
while(1<2){rect(0,0,1,1,col="yellow"); text(0.5,0.1,i); tic(1); i<-i+1}
 # Qui trovi come ottenere la seguente animazione
# Qui trovi come ottenere la seguente animazione



 # Qui come ottenere l'animazione di cui quella sopra a destra è un'istantanea
#
# Inserire locator(1) è un altro modo, molto comodo, per realizzare delle
# animazioni: occorre fare un CLIC per passare alla immagine successiva
# (title consente di mettere un titolo alla finestra; locator all'interno
# di parentesi grafiche non visualizza le coordinate del punto cliccato)
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f)
# clicca man mano la figura (se vuoi finire prima premi ESC)
for(a in -90:90) { persp(x,y,z, theta=30, phi = a, expand=0.5, col="green");
title(paste(a,"°")); locator(1) }
# Qui come ottenere l'animazione di cui quella sopra a destra è un'istantanea
#
# Inserire locator(1) è un altro modo, molto comodo, per realizzare delle
# animazioni: occorre fare un CLIC per passare alla immagine successiva
# (title consente di mettere un titolo alla finestra; locator all'interno
# di parentesi grafiche non visualizza le coordinate del punto cliccato)
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f)
# clicca man mano la figura (se vuoi finire prima premi ESC)
for(a in -90:90) { persp(x,y,z, theta=30, phi = a, expand=0.5, col="green");
title(paste(a,"°")); locator(1) }
 #
# Una animazione orientata col mouse (per finire premi ESC):
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f); teta <- 30; fi <- 40
while(TRUE) { persp(x,y,z, theta=teta, phi=fi, expand=0.5, col="green")
title(paste(teta,"° ",fi,"°")); l <- locator(1); a <- c(l$x,l$y)
fi <- ifelse(a[2] > 0, fi-1,fi+1); teta <- ifelse(a[1] > 0,teta-1,teta+1) }
# Invece di TRUE potevo mettere, ad es., 1 < 2
#
# Qui trovi come ottenere un'animazione relativa al grafico della
# funzione di due variabili considerata sopra.
# Qui trovi come ottenere l'orologio seguente:
#
# Una animazione orientata col mouse (per finire premi ESC):
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2,0.1)
z <- outer(x, y, f); teta <- 30; fi <- 40
while(TRUE) { persp(x,y,z, theta=teta, phi=fi, expand=0.5, col="green")
title(paste(teta,"° ",fi,"°")); l <- locator(1); a <- c(l$x,l$y)
fi <- ifelse(a[2] > 0, fi-1,fi+1); teta <- ifelse(a[1] > 0,teta-1,teta+1) }
# Invece di TRUE potevo mettere, ad es., 1 < 2
#
# Qui trovi come ottenere un'animazione relativa al grafico della
# funzione di due variabili considerata sopra.
# Qui trovi come ottenere l'orologio seguente:
 # Qui trovi un esempio relativo al concetto di continuità.
# Qui trovi un altro esempio di animazione; copia l'intero file e
# incollalo in R; ottieni la generazione passo passo della figura
# seguente a sinistra; con questo ottieni quella a destra.
# Qui trovi un esempio relativo al concetto di continuità.
# Qui trovi un altro esempio di animazione; copia l'intero file e
# incollalo in R; ottieni la generazione passo passo della figura
# seguente a sinistra; con questo ottieni quella a destra.
 # Ovviamente potrei ottenere i valori direttamente, a passi:
f <- function(x) x^2; x0 <- 2
h<- 10^-1; (f(x0+h)-f(x0))/h
[1] 4.1
...
h<- 10^-6; (f(x0+h)-f(x0))/h
[1] 4.000001
h<- 10^-7; (f(x0+h)-f(x0))/h
[1] 4
# o direttamente:
D(expression(x^2),"x")
2 * x
# O, per es., potrei procedere così ottenendo:
# Ovviamente potrei ottenere i valori direttamente, a passi:
f <- function(x) x^2; x0 <- 2
h<- 10^-1; (f(x0+h)-f(x0))/h
[1] 4.1
...
h<- 10^-6; (f(x0+h)-f(x0))/h
[1] 4.000001
h<- 10^-7; (f(x0+h)-f(x0))/h
[1] 4
# o direttamente:
D(expression(x^2),"x")
2 * x
# O, per es., potrei procedere così ottenendo:
 # Un esempio di
# Un esempio di  # Ecco una visione animata della stessa immagine guidata col mouse.
# Cliccando abbassa il punto di vista. Per smettere premi ESC
z <- array(c(0,0,0,0),dim=c(2,2))
teta <- 5; fi <- 50
while(1 < 2) {
pr<- persp(c(0,10),c(0,10),z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",
ylab="y",zlab="z",border="grey",phi=fi,theta=teta,box=FALSE,scale=TRUE,d=2)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
l <- locator(1); a <- c(l$x,l$y); fi <- ifelse(a[2] > 0, fi-1,fi+1)
teta <- ifelse(a[1] > 0,teta-1,teta+1); title(paste(teta,"° ",fi,"°")) }
#
# un altro esempio di ciclo di più righe (copia tutte le righe e
# incollale in R); è il calcolo dell'area di un cerchio approssimata
# per difetto e per eccesso mediante quadrettatura:
# Ecco una visione animata della stessa immagine guidata col mouse.
# Cliccando abbassa il punto di vista. Per smettere premi ESC
z <- array(c(0,0,0,0),dim=c(2,2))
teta <- 5; fi <- 50
while(1 < 2) {
pr<- persp(c(0,10),c(0,10),z,zlim=c(0,10),xlim=c(0,10),ylim=c(0,10),xlab="x",
ylab="y",zlab="z",border="grey",phi=fi,theta=teta,box=FALSE,scale=TRUE,d=2)
x<- seq(-20,30,len=200); lines(trans3d(x, z=0, y=(x-5)^2, pmat=pr),col="red")
l <- locator(1); a <- c(l$x,l$y); fi <- ifelse(a[2] > 0, fi-1,fi+1)
teta <- ifelse(a[1] > 0,teta-1,teta+1); title(paste(teta,"° ",fi,"°")) }
#
# un altro esempio di ciclo di più righe (copia tutte le righe e
# incollale in R); è il calcolo dell'area di un cerchio approssimata
# per difetto e per eccesso mediante quadrettatura:
 n <- 10
min<- 0; mag<-0; L<-1/n; for(i in 0:n) {for(j in 0:n) { #inizio
{x <- i*L; y <- j*L; d <- x*x+y*y}
{if(i>0 & j>0 & d<=1) min<-min+1; if (d<1) mag<-mag+1}}}
{r <- c(min/n^2*4, mag/n^2*4, (mag-min)/n^2*4)}; r; alarm() #fine
[1] 2.68 3.44 0.76
n <- 100
[1] 3.1016 3.1796 0.0780
n <- 200
[1] 3.1207 3.1602 0.0395
n <- 400
[1] 3.131400 3.151275 0.019875
# alarm(), se l'altoparlante del computer è attivato, produce
# un suono: può essere comodo per segnalare la fine di un ciclo.
#
# Si possono realizzare dei programmini per operare su piu' cifre.
# Vediamo ad es. come fare la somma tra interi di dimensioni qualunque:
x <- c(1,2,3,4); y <- c(1,2,3,4,5)
somma <- function(x,y) {z <- x
m <- length(x); n <- length(y)
# aggiungo degli 0 iniziali al numero piu' corto
if(m > n) y <- c(rep(0,times=m-n),y)
if(n > m) x <- c(rep(0,times=n-m),x)
n <- max(n,m)
# sommo le cifre e 1 se la somma delle precedenti cifre era > 9
r <- 0; for(i in n:1) { w <- x[i]+y[i]+r;
r <- ifelse (w>9,1,0); z[i] <- w-10*r}
if (r > 0) {n <- n+1; for(i in n:1) z[i+1] <- z[i]; z[1] <- 1}
z[1:n] }
somma(x,y)
[1] 1 3 5 7 9
# Possiamo copiarci le righe che definiscono "somma" e applicarle
per fare i calcoli che ci interessano
n <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
somma(n,n)
[1] 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0
# Quanto fa 2 alla 1000? Faccio 1000 raddoppi a partire da 1.
n <- c(1); for (t in 1:1000) {n <- somma(n,n)}; n
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
[31] 0 0 0 1 8 1 0 5 6 1 4 0 4 8 1 1 7 0 5 5 3 3 6 0 7 4 4 3 7 5
[61] 0 3 8 8 3 7 0 3 5 1 0 5 1 1 2 4 9 3 6 1 2 2 4 9 3 1 9 8 3 7
[91] 8 8 1 5 6 9 5 8 5 8 1 2 7 5 9 4 6 7 2 9 1 7 5 5 3 1 4 6 8 2
[121] 5 1 8 7 1 4 5 2 8 5 6 9 2 3 1 4 0 4 3 5 9 8 4 5 7 7 5 7 4 6
[151] 9 8 5 7 4 8 0 3 9 3 4 5 6 7 7 7 4 8 2 4 2 3 0 9 8 5 4 2 1 0
[181] 7 4 6 0 5 0 6 2 3 7 1 1 4 1 8 7 7 9 5 4 1 8 2 1 5 3 0 4 6 4
[211] 7 4 9 8 3 5 8 1 9 4 1 2 6 7 3 9 8 7 6 7 5 5 9 1 6 5 5 4 3 9
[241] 4 6 0 7 7 0 6 2 9 1 4 5 7 1 1 9 6 4 7 7 6 8 6 5 4 2 1 6 7 6
[271] 6 0 4 2 9 8 3 1 6 5 2 6 2 4 3 8 6 8 3 7 2 0 5 6 6 8 0 6 9 3
[301] 7 6
print(2^1000, 16) # controllo:
[1] 1.071508607186267e+301
# Vediamo ora come fare il prodotto tra interi di dimensioni qualunque:
prod <- function(a,b) {
# n = lungh. del numero piu' corto, a1 = num.lungo, b1 = num.corto
if(length(b) < length(a)) {n <- length(b); a1 <- a; b1 <- b}
else {n <- length(a); a1 <- b; b1 <- a}
# somma dei prodotti delle cifre di b1 per a1 (fatti come comme
# ripetute), aggiungendo via via uno 0 ad 1
tot <- 0; for (i in 1:n) {
s <- c(0); k <- n-i+1; if(b1[k] > 0) for(j in 1:b1[k]) s <- somma(s,a1)
a1 <- c(a1,0); tot <- somma(tot,s)}; tot}
u <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
v <- c(9,8,7,6,5,4,3,2,1)
prod(u,v)
[1] 1 2 1 9 3 2 6 3 1 1 2 4 8 2 8 5 3 2 1 1 1 2 6 3 5 2 6 9 0
# Possiamo poi calcolare potenze ad esponente naturale, fattoriali, ...
# Ricalcoliamo 2 alla 1000.
n <- 1; for (t in 1:1000) {n <- prod(n,2)}; n
# Riotteniamo, più lentamente:
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
...
[301] 7 6
# Calcoliamo un fattoriale:
print(factorial(30),16)
[1] 2.652528598121911e+32
p <- 1; for (i in 1:30) p <- prod(p,i); p
[1] 2 6 5 2 5 2 8 5 9 8 1 2 1 9 1 0 5 8 6 3 6 3 0 8 4 8 0 0 0 0 0 0 0
#
# I comandi utf8ToInt e intToUtf8 consentono di esplorare il codice (UTF8,
# simile all'ASCII) usato per codificare numericamente i caratteri (numeri
# in base 2, visualizzati in base dieci):
utf8ToInt("("); utf8ToInt("MaCoSa")
[1] 40
[1] 77 97 67 111 83 97
intToUtf8(40); intToUtf8(c(77,97,67,111,83,97))
[1] "("
[1] "MaCoSa"
# Si possono codificare segretamente i messaggi. Ecco un esempio semplice
# (facilmente "scopribile"): aggiungo 7 ai codici.
utf8ToInt("MaCoSa"); utf8ToInt("MaCoSa")+7
[1] 77 97 67 111 83 97
[1] 84 104 74 118 90 104
cod <- c(84,104,74,118,90,104); intToUtf8(cod); intToUtf8(cod-7)
[1] "ThJvZh"
[1] "MaCoSa"
# Ecco la codifica (32,33,35-91,93-126) dei caratteri usuali:
intToUtf8( c(32,33,seq(35,91)) )
[1] " !#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ["
intToUtf8( seq(93,126) )
[1] "]^_`abcdefghijklmnopqrstuvwxyz{|}~"
utf8ToInt(" 09AZaz")
[1] 32 48 57 65 90 97 122
#
# Un altro esempio di animazione (usa una finestra non troppo piccola):
coor <- c(-1,1,0,1); orig <- c(0,0)
yy <- c(-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1); xx <- c(0,0.25,0.5,0.75,1)
ce <- function(x) sqrt(1-(x^2))
n <- 30; for (i in 0:n) #inizio
{{plot(c(coor[1],coor[2]),c(coor[3],coor[4]),type="n",xlab="",ylab="",asp=1)}
{abline(h=xx,col="grey");abline(v=yy,col="grey");abline(h=0,col="blue")}
{curve(ce, add=TRUE,col="blue");x<-cos(pi/n*i);y<-sin(pi/n*i)}
{x1 <- c(-1,x,1); y1 <- c(0,y,0);lines(x1,y1);points(x*0.9,y*0.9)}
text(-7/8,0.9,"clicca"); locator(1)} #fine
n <- 10
min<- 0; mag<-0; L<-1/n; for(i in 0:n) {for(j in 0:n) { #inizio
{x <- i*L; y <- j*L; d <- x*x+y*y}
{if(i>0 & j>0 & d<=1) min<-min+1; if (d<1) mag<-mag+1}}}
{r <- c(min/n^2*4, mag/n^2*4, (mag-min)/n^2*4)}; r; alarm() #fine
[1] 2.68 3.44 0.76
n <- 100
[1] 3.1016 3.1796 0.0780
n <- 200
[1] 3.1207 3.1602 0.0395
n <- 400
[1] 3.131400 3.151275 0.019875
# alarm(), se l'altoparlante del computer è attivato, produce
# un suono: può essere comodo per segnalare la fine di un ciclo.
#
# Si possono realizzare dei programmini per operare su piu' cifre.
# Vediamo ad es. come fare la somma tra interi di dimensioni qualunque:
x <- c(1,2,3,4); y <- c(1,2,3,4,5)
somma <- function(x,y) {z <- x
m <- length(x); n <- length(y)
# aggiungo degli 0 iniziali al numero piu' corto
if(m > n) y <- c(rep(0,times=m-n),y)
if(n > m) x <- c(rep(0,times=n-m),x)
n <- max(n,m)
# sommo le cifre e 1 se la somma delle precedenti cifre era > 9
r <- 0; for(i in n:1) { w <- x[i]+y[i]+r;
r <- ifelse (w>9,1,0); z[i] <- w-10*r}
if (r > 0) {n <- n+1; for(i in n:1) z[i+1] <- z[i]; z[1] <- 1}
z[1:n] }
somma(x,y)
[1] 1 3 5 7 9
# Possiamo copiarci le righe che definiscono "somma" e applicarle
per fare i calcoli che ci interessano
n <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
somma(n,n)
[1] 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0 2 4 6 9 1 3 5 7 8 0
# Quanto fa 2 alla 1000? Faccio 1000 raddoppi a partire da 1.
n <- c(1); for (t in 1:1000) {n <- somma(n,n)}; n
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
[31] 0 0 0 1 8 1 0 5 6 1 4 0 4 8 1 1 7 0 5 5 3 3 6 0 7 4 4 3 7 5
[61] 0 3 8 8 3 7 0 3 5 1 0 5 1 1 2 4 9 3 6 1 2 2 4 9 3 1 9 8 3 7
[91] 8 8 1 5 6 9 5 8 5 8 1 2 7 5 9 4 6 7 2 9 1 7 5 5 3 1 4 6 8 2
[121] 5 1 8 7 1 4 5 2 8 5 6 9 2 3 1 4 0 4 3 5 9 8 4 5 7 7 5 7 4 6
[151] 9 8 5 7 4 8 0 3 9 3 4 5 6 7 7 7 4 8 2 4 2 3 0 9 8 5 4 2 1 0
[181] 7 4 6 0 5 0 6 2 3 7 1 1 4 1 8 7 7 9 5 4 1 8 2 1 5 3 0 4 6 4
[211] 7 4 9 8 3 5 8 1 9 4 1 2 6 7 3 9 8 7 6 7 5 5 9 1 6 5 5 4 3 9
[241] 4 6 0 7 7 0 6 2 9 1 4 5 7 1 1 9 6 4 7 7 6 8 6 5 4 2 1 6 7 6
[271] 6 0 4 2 9 8 3 1 6 5 2 6 2 4 3 8 6 8 3 7 2 0 5 6 6 8 0 6 9 3
[301] 7 6
print(2^1000, 16) # controllo:
[1] 1.071508607186267e+301
# Vediamo ora come fare il prodotto tra interi di dimensioni qualunque:
prod <- function(a,b) {
# n = lungh. del numero piu' corto, a1 = num.lungo, b1 = num.corto
if(length(b) < length(a)) {n <- length(b); a1 <- a; b1 <- b}
else {n <- length(a); a1 <- b; b1 <- a}
# somma dei prodotti delle cifre di b1 per a1 (fatti come comme
# ripetute), aggiungendo via via uno 0 ad 1
tot <- 0; for (i in 1:n) {
s <- c(0); k <- n-i+1; if(b1[k] > 0) for(j in 1:b1[k]) s <- somma(s,a1)
a1 <- c(a1,0); tot <- somma(tot,s)}; tot}
u <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0)
v <- c(9,8,7,6,5,4,3,2,1)
prod(u,v)
[1] 1 2 1 9 3 2 6 3 1 1 2 4 8 2 8 5 3 2 1 1 1 2 6 3 5 2 6 9 0
# Possiamo poi calcolare potenze ad esponente naturale, fattoriali, ...
# Ricalcoliamo 2 alla 1000.
n <- 1; for (t in 1:1000) {n <- prod(n,2)}; n
# Riotteniamo, più lentamente:
[1] 1 0 7 1 5 0 8 6 0 7 1 8 6 2 6 7 3 2 0 9 4 8 4 2 5 0 4 9 0 6
...
[301] 7 6
# Calcoliamo un fattoriale:
print(factorial(30),16)
[1] 2.652528598121911e+32
p <- 1; for (i in 1:30) p <- prod(p,i); p
[1] 2 6 5 2 5 2 8 5 9 8 1 2 1 9 1 0 5 8 6 3 6 3 0 8 4 8 0 0 0 0 0 0 0
#
# I comandi utf8ToInt e intToUtf8 consentono di esplorare il codice (UTF8,
# simile all'ASCII) usato per codificare numericamente i caratteri (numeri
# in base 2, visualizzati in base dieci):
utf8ToInt("("); utf8ToInt("MaCoSa")
[1] 40
[1] 77 97 67 111 83 97
intToUtf8(40); intToUtf8(c(77,97,67,111,83,97))
[1] "("
[1] "MaCoSa"
# Si possono codificare segretamente i messaggi. Ecco un esempio semplice
# (facilmente "scopribile"): aggiungo 7 ai codici.
utf8ToInt("MaCoSa"); utf8ToInt("MaCoSa")+7
[1] 77 97 67 111 83 97
[1] 84 104 74 118 90 104
cod <- c(84,104,74,118,90,104); intToUtf8(cod); intToUtf8(cod-7)
[1] "ThJvZh"
[1] "MaCoSa"
# Ecco la codifica (32,33,35-91,93-126) dei caratteri usuali:
intToUtf8( c(32,33,seq(35,91)) )
[1] " !#$%&'()*+,-./0123456789:;<=>?@ABCDEFGHIJKLMNOPQRSTUVWXYZ["
intToUtf8( seq(93,126) )
[1] "]^_`abcdefghijklmnopqrstuvwxyz{|}~"
utf8ToInt(" 09AZaz")
[1] 32 48 57 65 90 97 122
#
# Un altro esempio di animazione (usa una finestra non troppo piccola):
coor <- c(-1,1,0,1); orig <- c(0,0)
yy <- c(-1,-0.75,-0.5,-0.25,0,0.25,0.5,0.75,1); xx <- c(0,0.25,0.5,0.75,1)
ce <- function(x) sqrt(1-(x^2))
n <- 30; for (i in 0:n) #inizio
{{plot(c(coor[1],coor[2]),c(coor[3],coor[4]),type="n",xlab="",ylab="",asp=1)}
{abline(h=xx,col="grey");abline(v=yy,col="grey");abline(h=0,col="blue")}
{curve(ce, add=TRUE,col="blue");x<-cos(pi/n*i);y<-sin(pi/n*i)}
{x1 <- c(-1,x,1); y1 <- c(0,y,0);lines(x1,y1);points(x*0.9,y*0.9)}
text(-7/8,0.9,"clicca"); locator(1)} #fine
 # calcolo vettoriale
view <- c(-5,5, -5,5); orig <- c(0,0)
tx <- c(-5,-4,-3,-2,-1,0,1,2,3,4,5); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="",asp=1)
abline(h = ty,col="grey"); abline(v = tx, col="grey")
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
vect<- function(v,c) {lines(c(v[1],v[3]),c(v[2],v[4]),col=c);points(v[3],v[4],pch=".", cex=4,col=c)}
plus <- function(v,u) v+u-c(v[3],v[4])
v1 <- c(0,0,2,3); vect(v1,"blue")
v2 <- c(2,3,4,-1); vect(v2,"blue")
vect(plus(v1,v2),"red")
v3 <- c(2,4,4,2); vect(v3,"green4")
v4 <- c(4,2,-2,-3); vect(v4,"green4")
vect(plus(v3,v4),"orange3")
vect(-v2,"black")
# calcolo vettoriale
view <- c(-5,5, -5,5); orig <- c(0,0)
tx <- c(-5,-4,-3,-2,-1,0,1,2,3,4,5); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="",asp=1)
abline(h = ty,col="grey"); abline(v = tx, col="grey")
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
vect<- function(v,c) {lines(c(v[1],v[3]),c(v[2],v[4]),col=c);points(v[3],v[4],pch=".", cex=4,col=c)}
plus <- function(v,u) v+u-c(v[3],v[4])
v1 <- c(0,0,2,3); vect(v1,"blue")
v2 <- c(2,3,4,-1); vect(v2,"blue")
vect(plus(v1,v2),"red")
v3 <- c(2,4,4,2); vect(v3,"green4")
v4 <- c(4,2,-2,-3); vect(v4,"green4")
vect(plus(v3,v4),"orange3")
vect(-v2,"black")
 # alternativa usando il comando arrows (in cui metto
# in ordine le coordinate del 1º e del 2º punto)
view <- c(-2,8, -2,8); orig <- c(0,0)
tx <- seq(-2,8,1); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="", asp=1)
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
abline(h=orig[2],col="brown"); abline(v=orig[1],col="brown")
# length lughezza dei lati della freccia in pollici
v1 <- c(2,3,6,7); c1 <- "red"
v2 <- c(6,7,7,1); c2 <- "brown"
v3 <- c(2,3,7,1); c3 <- "blue"
v<- v1; color<- c1; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v2; color<- c2; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v3; color<- c3; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
# alternativa usando il comando arrows (in cui metto
# in ordine le coordinate del 1º e del 2º punto)
view <- c(-2,8, -2,8); orig <- c(0,0)
tx <- seq(-2,8,1); ty <- tx
plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="", asp=1)
abline(h=ty,col="grey60",lty=3); abline(v=tx, col="grey60",lty=3)
axis(1,pos=orig[2],label=FALSE,col="brown"); axis(2,pos=orig[1],label=FALSE,col="brown")
abline(h=orig[2],col="brown"); abline(v=orig[1],col="brown")
# length lughezza dei lati della freccia in pollici
v1 <- c(2,3,6,7); c1 <- "red"
v2 <- c(6,7,7,1); c2 <- "brown"
v3 <- c(2,3,7,1); c3 <- "blue"
v<- v1; color<- c1; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v2; color<- c2; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
v<- v3; color<- c3; arrows(v[1],v[2],v[3],v[4],length=0.15,col=color)
 #
# funzioni polinomiali di 2° grado (parabole) approssimanti dati (vedi)
#
# funzioni polinomiali di 2° grado (parabole) approssimanti dati (vedi)
 # interpolazione con spline (vedi)
# interpolazione con spline (vedi)
 # altro esempio (vedi)
# altro esempio (vedi)
 # medie mobili (vedi)
# medie mobili (vedi)

 #
# Vedi qui per la programmazione lineare
#
# Vedi qui per la matematica finanziaria
#
# un "cuore" (i colori in formato RGB: vedi)
# (ottenuto come fascio di curve di livello)
f <- function(x,y) x^2+((x^2)^(1/3)-y)^2
x <- seq(-20, 20, len=200)
y <- seq(-18, 20, len=200)
z <- outer(x, y, f)
contour(x,y,z,col="#FF8888",zlim=c(100,200),drawlabels=FALSE,nlev=100)
contour(x,y,z,col="#FF0000",zlim=c(200,300),drawlabels=FALSE,nlev=100,add=TRUE)
#
# Vedi qui per la programmazione lineare
#
# Vedi qui per la matematica finanziaria
#
# un "cuore" (i colori in formato RGB: vedi)
# (ottenuto come fascio di curve di livello)
f <- function(x,y) x^2+((x^2)^(1/3)-y)^2
x <- seq(-20, 20, len=200)
y <- seq(-18, 20, len=200)
z <- outer(x, y, f)
contour(x,y,z,col="#FF8888",zlim=c(100,200),drawlabels=FALSE,nlev=100)
contour(x,y,z,col="#FF0000",zlim=c(200,300),drawlabels=FALSE,nlev=100,add=TRUE)
 # un'altra animazione:
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
view <- c(0,100, 0,70)
for (k in 59:0) {plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="") #inizio
abline(h=k+1,col="blue");abline(h=k+1.25,col="blue");abline(h=k+1.5,col="blue")
if (k>0) for (i in 1:99) for (j in 1:k) if (runif(1)<0.03) points(i,j,col="blue");tic(0.3)} #fine
# un'altra animazione:
tic <- function(x) {sec <-proc.time()[3]; while(proc.time()[3] < sec+x) sec<-sec} # passano x sec
view <- c(0,100, 0,70)
for (k in 59:0) {plot(c(view[1],view[2]),c(view[3],view[4]),type="n",xlab="",ylab="") #inizio
abline(h=k+1,col="blue");abline(h=k+1.25,col="blue");abline(h=k+1.5,col="blue")
if (k>0) for (i in 1:99) for (j in 1:k) if (runif(1)<0.03) points(i,j,col="blue");tic(0.3)} #fine
 #
# Per inciso, osserviamo che si possono realizzare grafi ad albero in
# vari modi. Si veda l'help in linea per dettagli. Qui vediamo solo
# come realizzare grafi opportunamente "bilanciati" caricando la libreria
# "cluster" e utilizzando il comando pltree (e il comando agnes:
# Agglomerative Nesting):
library(cluster)
cosa <- c(1,2,3,4,5,6,7,8)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9,10)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
#
# Per inciso, osserviamo che si possono realizzare grafi ad albero in
# vari modi. Si veda l'help in linea per dettagli. Qui vediamo solo
# come realizzare grafi opportunamente "bilanciati" caricando la libreria
# "cluster" e utilizzando il comando pltree (e il comando agnes:
# Agglomerative Nesting):
library(cluster)
cosa <- c(1,2,3,4,5,6,7,8)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,3,4,5,6,7,8,9,10)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
 cosa <- c(1,1,2,2,3)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,2,3,3,4,4)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,1,2,2,3,3,4,5); Cosa <- c("a","a","b","b","c","c","d","e")
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=Cosa)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=FALSE)
cosa <- c(1,1,2,2,3)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,2,2,3,3,4,4)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n")
cosa <- c(1,1,2,2,3,3,4,5); Cosa <- c("a","a","b","b","c","c","d","e")
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=Cosa)
pltree(agnes(cosa),ylab=NULL,main=NULL,yaxt="n",labels=FALSE)


 #
# Come verificare l'equivalenza di 2 termini con più variabili che stanno
# in dati intervalli con il generatore di numeri casuali (se ne hanno
# solo una basta farlo confrontandone i grafici). Esempio:
a1 <- function(x,y) sin(x)-sin(y)
a2 <- function(x,y) 2*sin((x-y)/2)*cos((x+y)/2)
x1 <- -pi; x2 <- 2*pi; x <- x1+runif(12)*(x2-x1)
y1 <- -pi; y2 <- 2*pi; y <- y1+runif(12)*(y2-y1)
a1(x,y); a2(x,y)
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
# Con ulteriori prove ho una conferma (non una prova) dell'equivalenza.
# Per una conferma simbolica posso usare wolframalpha.com: se metto in input
# 2*sin((x-y)/2)*cos((x+y)/2) ottengo la semplificazione sin(x)-sin(y)
# (e molte altre cose ...)
#
# Sui grafici o in pagine apposite posso scrivere formule complesse
# così come le scriverei "a mano". Qualche esempio:
# (bg="…" serve solo per fare giallo lo sfondo)
par( mai = c(0,0,0,0), bg="#FFFF99" )
plot(c(0,10),c(0,10),type="n")
text(2,8,expression(A[2]))
# invece di expression si può usare quote
text(2,5,expression(lim(frac(1,2^n),n %->% infinity)))
text(2,2,expression("k = "*bgroup("(",atop(m,n),")")))
# o text(2,2,expression("k = "~bgroup("(",atop(m,n),")")))
text(5,8,expression(frac(a+b,frac(c+b,2^n))~+1))
text(5,5,expression(integral(f(x)*dx,a,b)))
# il simbolo ~ introduce uno spazio bianco (copialo da qui se non
# riesci a batterlo)
text(5,2,expression(integral(f(x)*~dx,a,b)))
text(8,8,expression(widehat(ABC)))
text(8,5,expression(hat(ABC)))
text(8,2,expression(bar(ABC)))
#
# Come verificare l'equivalenza di 2 termini con più variabili che stanno
# in dati intervalli con il generatore di numeri casuali (se ne hanno
# solo una basta farlo confrontandone i grafici). Esempio:
a1 <- function(x,y) sin(x)-sin(y)
a2 <- function(x,y) 2*sin((x-y)/2)*cos((x+y)/2)
x1 <- -pi; x2 <- 2*pi; x <- x1+runif(12)*(x2-x1)
y1 <- -pi; y2 <- 2*pi; y <- y1+runif(12)*(y2-y1)
a1(x,y); a2(x,y)
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
[1] 0.37590448 -1.82230467 1.00966406 -0.63148250 0.38496151 -1.07305543
[7] 0.35084118 -0.49564276 -0.88333351 -1.79092944 -0.17837395 -0.07969682
# Con ulteriori prove ho una conferma (non una prova) dell'equivalenza.
# Per una conferma simbolica posso usare wolframalpha.com: se metto in input
# 2*sin((x-y)/2)*cos((x+y)/2) ottengo la semplificazione sin(x)-sin(y)
# (e molte altre cose ...)
#
# Sui grafici o in pagine apposite posso scrivere formule complesse
# così come le scriverei "a mano". Qualche esempio:
# (bg="…" serve solo per fare giallo lo sfondo)
par( mai = c(0,0,0,0), bg="#FFFF99" )
plot(c(0,10),c(0,10),type="n")
text(2,8,expression(A[2]))
# invece di expression si può usare quote
text(2,5,expression(lim(frac(1,2^n),n %->% infinity)))
text(2,2,expression("k = "*bgroup("(",atop(m,n),")")))
# o text(2,2,expression("k = "~bgroup("(",atop(m,n),")")))
text(5,8,expression(frac(a+b,frac(c+b,2^n))~+1))
text(5,5,expression(integral(f(x)*dx,a,b)))
# il simbolo ~ introduce uno spazio bianco (copialo da qui se non
# riesci a batterlo)
text(5,2,expression(integral(f(x)*~dx,a,b)))
text(8,8,expression(widehat(ABC)))
text(8,5,expression(hat(ABC)))
text(8,2,expression(bar(ABC)))
 # Le stesse cose si ottengono se si usa bquote, che consente anche di sostituire
# valori alle variabili. Un esempio:
text(1.5,1,bquote( integral(F(t)~dt,a,b)~" ="~ F(b) - F(a)))
a=2; text(5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
a="c"; text(8.5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
# Quanto racchiusa in .(…) un'espressione viene visualizzata col suo valore.
# Le stesse cose si ottengono se si usa bquote, che consente anche di sostituire
# valori alle variabili. Un esempio:
text(1.5,1,bquote( integral(F(t)~dt,a,b)~" ="~ F(b) - F(a)))
a=2; text(5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
a="c"; text(8.5,1,bquote( integral(F(t)~dt,.(a),b)~" ="~ F(b) - F(.(a))))
# Quanto racchiusa in .(…) un'espressione viene visualizzata col suo valore.
 # Sono scritte in Teχ. Vedi qui per altri esempi.
# Sono scritte in Teχ. Vedi qui per altri esempi.