R. USI STATISTICI AVANZATI - in costruzione (altri usi)
Nel programma i comandi
appaiono preceduti da >. Le righe seguenti, scritte in nero (con
eventuali parti in rosso),
possono man mano essere copiate da qui e incollate in R. Il
programma automaticamente le esegue. Le cose scritte in blu sono le uscite
od altri commenti. I grafici, qui riprodotti, in R appaiono in altre finestre.
Rimandiamo a documento "usi di base" per
l'uso dell'help e dei comandi essenziali.
Rimandiamo agli Oggetti Matematici e a
WikiPedia (inglese) per approfondimenti di statistica.
ancora dati da rete dist.interquartile varianza e scarto qua. medio
tabelle di dati ancora (bis) dati da rete o da file su computer
estrazione variabili da tabella ancora (ter) dati da rete correlazione
sottoinsiemi di dati grafici regressione regressione vincolata
componenti principali test chi^2,student funz.quadratica approssimante
tabelle dati classif. gaussiana esponenziale graf.densità bivariata
binomiale poissoniana affiancare grafici librerie esterne
affiancare testo e grafici finestre di testo tipi di comandi di R
Indice alfabetico comandi - Indice alfabetico generale attività
# Ricordiamo che i dati possono essere anche recuperati dal computer o,
# in rete senza dei copia/incolla; ad esempio col comando:
readLines("http://macosa.dima.unige.it/om/prg/R/alunne.txt", n=5)
# leggiamo le prime 5 righe del file. Vediamole tutte (in questo caso
# sono poche:
readLines("http://macosa.dima.unige.it/om/prg/R/alunne.txt")
[1] "# altezze alunne" "156" "168" "162"
[5] "150" "167" "157" "170"
[9] "157" "159" "164" "157"
[13] "165" "163" "165" "166"
[17] "160" "163" "162" "155"
[21] "" ""
# Per la stampa senza virgolette basta battere noquote( readLines("http ...") )
# (il comando "noquote" può essere usato anche in altri contesti)
# Vediamo il contenuto del file alunne.txt presente in rete;
# vediamo che la prima riga è un commento; allora col seguente
# comando metto in "dati" il file saltando con skip 1 riga
dati <- scan("http://macosa.dima.unige.it/om/prg/R/alunne.txt", skip=1)
dati
[1] 156 168 162 150 167 157 170 157 159 164 157 165 163 165 166 160
[17] 163 162 155
# la funzione IQR calcola la distanza interquartile
summary(dati)
Min. 1st Qu. Median Mean 3rd Qu. Max.
150.0 157.0 162.0 161.4 165.0 170.0
IQR(dati)
[1] 8
# var e sd indicano gli stimatori non distorti della varianza e dello scarto
# quadratico medio (standard deviation), ossia (se sono i dati sono n) la varianza
# moltiplicata per n/(n-1) e la sua radice quadrata. Ricordo che la "deviazione
# standard della media" è invece la deviazione standard divisa per la radice
# della numerosità dei dati: sd(dati)/sqrt(length(dati)). Definiamo due
# funzioni var2 e sd2 per indicare la varianza e lo scarto q.m. "teorici" (in
# contrapposizione a quelli "statistici" o "campionari" considerati sopra):
var2 <- function(dati) mean((dati-mean(dati))^2)
sd2 <- function(x) sqrt(var2(x)) # o sd2 <- function(x) sqrt(mean((x-mean(x))^2))
var(dati); sd(dati); sd(dati)^2
[1] 26.35673
[1] 5.13388
[1] 26.35673
var2(dati); sd2(dati); sd2(dati)^2
[1] 24.96953
[1] 4.996952
[1] 24.96953
#
# Per avere degli indicatori numerici della asimmetria (skewness) di una
# distribuzione di dati vedi qui.
#
# Vediamo ora come analizzare una tabella di dati. Vediamo prima una
# tabella introdotta direttamente (array indica una variabile indiciata;
# qui è di 6 righe e 4 colonne - i dati sono letti colonna per colonna -
# ma potrebbere anche essere una tabella con più di 2 dimensioni)
# (una array, in R, ha 1, 2 o più dimensioni, una matrix ne ha 2)
z <- c(1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4)
t <- array(z,dim=c(6,4)); t
[,1] [,2] [,3] [,4]
[1,] 1 7 3 9
[2,] 2 8 4 0
[3,] 3 9 5 1
[4,] 4 0 6 2
[5,] 5 1 7 3
[6,] 6 2 8 4
# [ con matrix avrei scritto:
# t <- matrix(z, nrow=6, ncol=4); t ]
# gli indici dei posti sono richiamati tra parentesi quadre
t[2,4]
[1] 0
# col comando write posso scrivere i dati in un file o, mettendo file="",
# sullo schermo; con sep = "\t" ordino di separare i dati con il
# tabulatore; con ncolumns specifico il numero delle colonne; i dati
# vengono scritti nello stesso ordine in cui sono scritti, riga per riga
write( z , file="", sep = "\t", ncolumns=6)
1 2 3 4 5 6
7 8 9 0 1 2
3 4 5 6 7 8
9 0 1 2 3 4
# mettendo in sep altro ...
write( z , file="", sep = " -- ", ncolumns=6)
1 -- 2 -- 3 -- 4 -- 5 -- 6
7 -- 8 -- 9 -- 0 -- 1 -- 2
3 -- 4 -- 5 -- 6 -- 7 -- 8
9 -- 0 -- 1 -- 2 -- 3 -- 4
# Usando il comando edit vedo i dati in una tabella stile "foglio di calcolo"
# (che poi chiudo cliccando l'apposito bottone). I dati sono poi visualizzati
# nella pagina (con "edit" posso anche vedere altri oggetti definiti)
# Se voglio vedere solo la tabella uso data.entry.
data.entry(t)
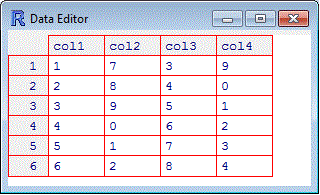 #
# Ecco alcune prime elaborazioni:
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# ecco una rapida analisi delle colonne
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# come analizzare i dati della prima colonna
a <- t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# e quelli della sesta riga
b <- t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# gli stessi dati organizzati in una tabella 3×8
u <- array(z,dim=c(3,8)); u
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 4 7 0 3 6 9 2
[2,] 2 5 8 1 4 7 0 3
[3,] 3 6 9 2 5 8 1 4
#
# Conviene analizzare tabelle di dati gia' memorizzati come file distinti; se
# sei in rete puoi analizzare direttamente il file seguente, che puoi
# richiamare dal browser mettendo il nome (usando "/", non "\")
# http://macosa.dima.unige.it/sosta/dati3.txt come argomento di
# read.table o puoi copiare da qui sotto (dalla riga "peso altezza ..."
# alla riga "4 60 170 m"), incollare in un file di testo a cui dare un
# nome (ad es. lo stesso, dati3.txt), scegliere col comando Change Dir
# (dal menù File) la cartella del computer in cui lo hai messo (che può
# essere esaminata col comando dir() - solo dir ne dà il percorso) e poi
# mettere dati <- read.table("dati3.txt") invece di:
dati <- read.table("http://macosa.dima.unige.it/sosta/dati3.txt")
# se azionassi dati otterrei:
peso altezza sesso
1 65 184 m
2 71 192 f
3 59 163 f
4 60 170 m
# [ in ogni caso (come spiegato più avanti) conviene esaminare un
# po' di righe del file con readLines(..., n=...) ]
# [Nota: dir() stampa tutto il contenuto della cartella (directory) corrente,
# dir(..) quello della cartella soprastante, dir(../..) quello di quella che
# la contiene, ...; usando in modo analogo list.dirs si ha la stampa delle
# sole cartelle, non dei file]
# In questo caso è facile esaminare le dimensioni della tabella, ma in
# generale conviene (prima di una sua eventuale stampa, se non è troppo
# lunga) usare il comando dim per sapere quante sono righe e colonne:
dim(dati)
[1] 4 3
summary(dati)
peso altezza sesso
Min. :59.00 Min. :163.0 f:2
1st Qu.:59.75 1st Qu.:168.2 m:2
Median :62.50 Median :177.0
Mean :63.75 Mean :177.2
3rd Qu.:66.50 3rd Qu.:186.0
Max. :71.00 Max. :192.0
# per estrarre una singola variabile dalla tabella puoi usare $:
a <- dati$peso
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
59.00 59.75 62.50 63.75 66.50 71.00
#
# Oltre che con read.table, abbiamo visto come con read.csv2 si possono
# leggere dati da una tabella, quando in particolare sono in un foglio
# di calcolo. Analogamente con write.csv e write.csv2 si può copiare una
# tabella di dati in un foglio di calcolo, usando "." o "," per separare
# parte intera e parte frazionaria. Ad es. i dati precedenti con il
# seguente comando vengono messi nel file tabel.csv
write.csv(dati,file = "tabel.csv")
#
# Questo è il modo standard in cui sono memorizzati i dati; ma
# il programma è in grado di analizzare dati regitrstati quasi in
# ogni modo; vediamo un esempio, in cui usiamo i comandi readLines
# per analizzare i file e read.table (o read.delim) per caricarli:
# [puoi azionare help(read.table) per dettagli]
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab")
[1] "'tabella (indagine su studenti di un corso universitario - dati tratti da"
[2] "'un esempio riportato nel manuale di MiniTab)"
[3] "'a: battiti prima di eventuale corsa di 1 min"
[4] "'b: battiti dopo"
[5] "'c: fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[6] "'d: fumatore (1 si`;0 no)"
[7] "'e: sesso (1 M; 2 F)"
[8] "'f: altezza"
[9] "'g: peso"
[10] "'h: attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[11] " 64; 88;1;0;1;168;64;2"
...
# Ma conviene, per non riempire lo schermo e per vedere solo come sono
# introdotti i dati, delimitare le righe da vedere con n =
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab",n=11)
#
# nel comando metto header=FALSE per indicare che non c'è una
# intestazione delle colonne, skip=10 per indicare le righe da saltare,
# sep=";" per specificare qual è l'elemento di separazione tra i dati
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
# ovvero
dati <- read.delim("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
dati
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
4 66 78 1 1 1 184 86 1
5 64 80 1 0 1 176 70 2
6 74 84 1 0 1 184 75 1
7 84 84 1 0 1 184 68 3
...
89 78 80 0 0 2 173 60 1
90 68 68 0 0 2 159 50 2
91 86 84 0 0 2 171 68 3
92 76 76 0 0 2 156 49 2
# Un modo comodo (e non ingombrante) per capire che cosa si sta
# analizzando è usare il comando str (struttura):
str(dati)
'data.frame': 92 obs. of 8 variables:
$ V1: int 64 58 62 66 64 74 84 68 62 76 ...
$ V2: int 88 70 76 78 80 84 84 72 75 118 ...
$ V3: int 1 1 1 1 1 1 1 1 1 1 ...
$ V4: int 0 0 1 1 0 0 0 0 0 0 ...
$ V5: int 1 1 1 1 1 1 1 1 1 1 ...
$ V6: int 168 183 186 184 176 184 184 188 184 181 ...
$ V7: int 64 66 73 86 70 75 68 86 88 63 ...
$ V8: int 2 2 3 1 2 1 3 2 2 2 ...
summary(dati)
V1 V2 V3 V4
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V5 V6 V7 V8
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# le colonne, in assenza di intestazioni, sono intestate automaticamente
# (dalle prime righe del file capisco che V1 sono i battiti prima
# della corsa, ..., V6 sono le altezze, ...)
a1 <- dati$V1; summary(a1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(a1)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
hist(a1,right=FALSE)
hist(a1,seq(40,100,10), right=FALSE)
#
# Ecco alcune prime elaborazioni:
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# ecco una rapida analisi delle colonne
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# come analizzare i dati della prima colonna
a <- t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# e quelli della sesta riga
b <- t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# gli stessi dati organizzati in una tabella 3×8
u <- array(z,dim=c(3,8)); u
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 4 7 0 3 6 9 2
[2,] 2 5 8 1 4 7 0 3
[3,] 3 6 9 2 5 8 1 4
#
# Conviene analizzare tabelle di dati gia' memorizzati come file distinti; se
# sei in rete puoi analizzare direttamente il file seguente, che puoi
# richiamare dal browser mettendo il nome (usando "/", non "\")
# http://macosa.dima.unige.it/sosta/dati3.txt come argomento di
# read.table o puoi copiare da qui sotto (dalla riga "peso altezza ..."
# alla riga "4 60 170 m"), incollare in un file di testo a cui dare un
# nome (ad es. lo stesso, dati3.txt), scegliere col comando Change Dir
# (dal menù File) la cartella del computer in cui lo hai messo (che può
# essere esaminata col comando dir() - solo dir ne dà il percorso) e poi
# mettere dati <- read.table("dati3.txt") invece di:
dati <- read.table("http://macosa.dima.unige.it/sosta/dati3.txt")
# se azionassi dati otterrei:
peso altezza sesso
1 65 184 m
2 71 192 f
3 59 163 f
4 60 170 m
# [ in ogni caso (come spiegato più avanti) conviene esaminare un
# po' di righe del file con readLines(..., n=...) ]
# [Nota: dir() stampa tutto il contenuto della cartella (directory) corrente,
# dir(..) quello della cartella soprastante, dir(../..) quello di quella che
# la contiene, ...; usando in modo analogo list.dirs si ha la stampa delle
# sole cartelle, non dei file]
# In questo caso è facile esaminare le dimensioni della tabella, ma in
# generale conviene (prima di una sua eventuale stampa, se non è troppo
# lunga) usare il comando dim per sapere quante sono righe e colonne:
dim(dati)
[1] 4 3
summary(dati)
peso altezza sesso
Min. :59.00 Min. :163.0 f:2
1st Qu.:59.75 1st Qu.:168.2 m:2
Median :62.50 Median :177.0
Mean :63.75 Mean :177.2
3rd Qu.:66.50 3rd Qu.:186.0
Max. :71.00 Max. :192.0
# per estrarre una singola variabile dalla tabella puoi usare $:
a <- dati$peso
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
59.00 59.75 62.50 63.75 66.50 71.00
#
# Oltre che con read.table, abbiamo visto come con read.csv2 si possono
# leggere dati da una tabella, quando in particolare sono in un foglio
# di calcolo. Analogamente con write.csv e write.csv2 si può copiare una
# tabella di dati in un foglio di calcolo, usando "." o "," per separare
# parte intera e parte frazionaria. Ad es. i dati precedenti con il
# seguente comando vengono messi nel file tabel.csv
write.csv(dati,file = "tabel.csv")
#
# Questo è il modo standard in cui sono memorizzati i dati; ma
# il programma è in grado di analizzare dati regitrstati quasi in
# ogni modo; vediamo un esempio, in cui usiamo i comandi readLines
# per analizzare i file e read.table (o read.delim) per caricarli:
# [puoi azionare help(read.table) per dettagli]
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab")
[1] "'tabella (indagine su studenti di un corso universitario - dati tratti da"
[2] "'un esempio riportato nel manuale di MiniTab)"
[3] "'a: battiti prima di eventuale corsa di 1 min"
[4] "'b: battiti dopo"
[5] "'c: fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[6] "'d: fumatore (1 si`;0 no)"
[7] "'e: sesso (1 M; 2 F)"
[8] "'f: altezza"
[9] "'g: peso"
[10] "'h: attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[11] " 64; 88;1;0;1;168;64;2"
...
# Ma conviene, per non riempire lo schermo e per vedere solo come sono
# introdotti i dati, delimitare le righe da vedere con n =
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab",n=11)
#
# nel comando metto header=FALSE per indicare che non c'è una
# intestazione delle colonne, skip=10 per indicare le righe da saltare,
# sep=";" per specificare qual è l'elemento di separazione tra i dati
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
# ovvero
dati <- read.delim("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
dati
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
4 66 78 1 1 1 184 86 1
5 64 80 1 0 1 176 70 2
6 74 84 1 0 1 184 75 1
7 84 84 1 0 1 184 68 3
...
89 78 80 0 0 2 173 60 1
90 68 68 0 0 2 159 50 2
91 86 84 0 0 2 171 68 3
92 76 76 0 0 2 156 49 2
# Un modo comodo (e non ingombrante) per capire che cosa si sta
# analizzando è usare il comando str (struttura):
str(dati)
'data.frame': 92 obs. of 8 variables:
$ V1: int 64 58 62 66 64 74 84 68 62 76 ...
$ V2: int 88 70 76 78 80 84 84 72 75 118 ...
$ V3: int 1 1 1 1 1 1 1 1 1 1 ...
$ V4: int 0 0 1 1 0 0 0 0 0 0 ...
$ V5: int 1 1 1 1 1 1 1 1 1 1 ...
$ V6: int 168 183 186 184 176 184 184 188 184 181 ...
$ V7: int 64 66 73 86 70 75 68 86 88 63 ...
$ V8: int 2 2 3 1 2 1 3 2 2 2 ...
summary(dati)
V1 V2 V3 V4
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V5 V6 V7 V8
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# le colonne, in assenza di intestazioni, sono intestate automaticamente
# (dalle prime righe del file capisco che V1 sono i battiti prima
# della corsa, ..., V6 sono le altezze, ...)
a1 <- dati$V1; summary(a1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(a1)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
hist(a1,right=FALSE)
hist(a1,seq(40,100,10), right=FALSE)
 # Come sovrapporre gli istogrammi di due sottopopolazioni.
# Vedi qui per l'es. seguente (altezze maschi e femmine)
# Come sovrapporre gli istogrammi di due sottopopolazioni.
# Vedi qui per l'es. seguente (altezze maschi e femmine)
 # Come estrarre/togliere righe o colonne da una tabella
# Vedi qui per un esempio.
# Come unire tabelle. Vedi qui per un esempio.
#
# i coefficienti di correlazione tra le diverse variabili
# [ vedi qui per come associare ad essi un intervallo di indeterminazione ]
cor(dati)
V1 V2 V3 V4
V1 1.00000000 0.61619572 0.052277524 0.12870465
V2 0.61619572 1.00000000 0.576816142 0.04585426
V3 0.05227752 0.57681614 1.000000000 0.06558148
V4 0.12870465 0.04585426 0.065581483 1.00000000
V5 0.28539261 0.30947898 -0.106766917 -0.12904743
V6 -0.21102575 -0.15326188 0.223595030 0.04278398
V7 -0.20322133 -0.16637381 0.224024008 0.20061688
V8 -0.06256772 -0.14110121 0.007323575 -0.12020183
V5 V6 V7 V8
V1 0.2853926 -0.21102575 -0.203221327 -0.062567716
V2 0.3094790 -0.15326188 -0.166373807 -0.141101211
V3 -0.1067669 0.22359503 0.224024008 0.007323575
V4 -0.1290474 0.04278398 0.200616884 -0.120201834
V5 1.0000000 -0.70902885 -0.710227077 -0.104971238
V6 -0.7090288 1.00000000 0.782633130 0.089299812
V7 -0.7102271 0.78263313 1.000000000 -0.004037995
V8 -0.1049712 0.08929981 -0.004037995 1.000000000
# Per avere meno (o più) cifre possiamo usare print e round
print(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V2 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V3 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V4 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V5 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.7090 -0.71023 -0.10497
V6 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V7 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V8 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
round(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V2 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V3 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V4 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V5 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V6 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V7 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V8 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
# estrazione dei dati relativi ai maschi
subset(dati,dati$V5==1)
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
...
67 74 76 0 0 1 170 56 2
68 68 66 0 0 1 172 70 2
# la nuova matrice di correlazione, da cui si vede che, per es.,
# la correlazione tra altezza (V6) e peso (V7) passa da 0.78 a
# 0.59
cor(subset(dati,dati$V5==1))
V1 V2 V3 V4 V5 V6
V1 1.00000000 0.60734884 -0.01479404 0.0580805261 NA 0.0449853579
V2 0.60734884 1.00000000 0.48164645 -0.0157001769 NA 0.0559294175
V3 -0.01479404 0.48164645 1.00000000 -0.0313496568 NA 0.1609605822
V4 0.05808053 -0.01570018 -0.03134966 1.0000000000 NA 0.0003936642
V5 NA NA NA NA 1 NA
V6 0.04498536 0.05592942 0.16096058 0.0003936642 NA 1.0000000000
V7 -0.09475028 -0.06564303 0.18162068 0.1750103679 NA 0.5904647568
V8 0.04484415 -0.11115295 0.01163105 -0.1804916067 NA 0.0525792792
V7 V8
V1 -0.09475028 0.04484415
V2 -0.06564303 -0.11115295
V3 0.18162068 0.01163105
V4 0.17501037 -0.18049161
V5 NA NA
V6 0.59046476 0.05257928
V7 1.00000000 -0.13112832
V8 -0.13112832 1.00000000
Warning message:
In cor(subset(dati, dati$V5 == 1)) : the standard deviation is zero
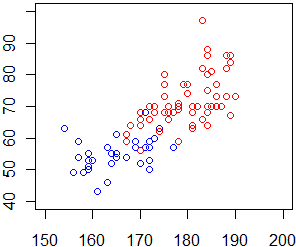
# la spiegazione "grafica" del fenomeno (i punti relativi all'intero
# campione e quelli relativi ai maschi)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="")
points(dati$V6,dati$V7,col="blue")
points(subset(dati$V6,dati$V5==1),subset(dati$V7,dati$V5==1),col="red")
# Come estrarre/togliere righe o colonne da una tabella
# Vedi qui per un esempio.
# Come unire tabelle. Vedi qui per un esempio.
#
# i coefficienti di correlazione tra le diverse variabili
# [ vedi qui per come associare ad essi un intervallo di indeterminazione ]
cor(dati)
V1 V2 V3 V4
V1 1.00000000 0.61619572 0.052277524 0.12870465
V2 0.61619572 1.00000000 0.576816142 0.04585426
V3 0.05227752 0.57681614 1.000000000 0.06558148
V4 0.12870465 0.04585426 0.065581483 1.00000000
V5 0.28539261 0.30947898 -0.106766917 -0.12904743
V6 -0.21102575 -0.15326188 0.223595030 0.04278398
V7 -0.20322133 -0.16637381 0.224024008 0.20061688
V8 -0.06256772 -0.14110121 0.007323575 -0.12020183
V5 V6 V7 V8
V1 0.2853926 -0.21102575 -0.203221327 -0.062567716
V2 0.3094790 -0.15326188 -0.166373807 -0.141101211
V3 -0.1067669 0.22359503 0.224024008 0.007323575
V4 -0.1290474 0.04278398 0.200616884 -0.120201834
V5 1.0000000 -0.70902885 -0.710227077 -0.104971238
V6 -0.7090288 1.00000000 0.782633130 0.089299812
V7 -0.7102271 0.78263313 1.000000000 -0.004037995
V8 -0.1049712 0.08929981 -0.004037995 1.000000000
# Per avere meno (o più) cifre possiamo usare print e round
print(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V2 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V3 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V4 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V5 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.7090 -0.71023 -0.10497
V6 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V7 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V8 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
round(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V2 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V3 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V4 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V5 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V6 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V7 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V8 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
# estrazione dei dati relativi ai maschi
subset(dati,dati$V5==1)
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
...
67 74 76 0 0 1 170 56 2
68 68 66 0 0 1 172 70 2
# la nuova matrice di correlazione, da cui si vede che, per es.,
# la correlazione tra altezza (V6) e peso (V7) passa da 0.78 a
# 0.59
cor(subset(dati,dati$V5==1))
V1 V2 V3 V4 V5 V6
V1 1.00000000 0.60734884 -0.01479404 0.0580805261 NA 0.0449853579
V2 0.60734884 1.00000000 0.48164645 -0.0157001769 NA 0.0559294175
V3 -0.01479404 0.48164645 1.00000000 -0.0313496568 NA 0.1609605822
V4 0.05808053 -0.01570018 -0.03134966 1.0000000000 NA 0.0003936642
V5 NA NA NA NA 1 NA
V6 0.04498536 0.05592942 0.16096058 0.0003936642 NA 1.0000000000
V7 -0.09475028 -0.06564303 0.18162068 0.1750103679 NA 0.5904647568
V8 0.04484415 -0.11115295 0.01163105 -0.1804916067 NA 0.0525792792
V7 V8
V1 -0.09475028 0.04484415
V2 -0.06564303 -0.11115295
V3 0.18162068 0.01163105
V4 0.17501037 -0.18049161
V5 NA NA
V6 0.59046476 0.05257928
V7 1.00000000 -0.13112832
V8 -0.13112832 1.00000000
Warning message:
In cor(subset(dati, dati$V5 == 1)) : the standard deviation is zero
# la spiegazione "grafica" del fenomeno (i punti relativi all'intero
# campione e quelli relativi ai maschi)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="")
points(dati$V6,dati$V7,col="blue")
points(subset(dati$V6,dati$V5==1),subset(dati$V7,dati$V5==1),col="red")
 # la retta di regressione (altezza, peso); lm sta per linear model
x <- dati$V6; y <- dati$V7; plot(x,y)
mod = lm(y ~ x); mod$coefficients; abline(mod)
(Intercept) x
-90.8681981 0.8983596
# y = -90.87 + 0.8984 x (per abline vedi)
# I coeff. potrei memorizzarli con
# b <- mod$coefficients[1]; a <- mod$coefficients[2]
# Nota: confint(lm(y~x),level=…) dà intervalli di confidenza per lm (vedi l'help)
# [ se non trovi ~ nella tastiera, se non hai sottomano questo documento da cui
# copiarlo, … puoi usare help(tilde) e copiarlo dalla pagina che si apre ]
# la retta di regressione (altezza, peso); lm sta per linear model
x <- dati$V6; y <- dati$V7; plot(x,y)
mod = lm(y ~ x); mod$coefficients; abline(mod)
(Intercept) x
-90.8681981 0.8983596
# y = -90.87 + 0.8984 x (per abline vedi)
# I coeff. potrei memorizzarli con
# b <- mod$coefficients[1]; a <- mod$coefficients[2]
# Nota: confint(lm(y~x),level=…) dà intervalli di confidenza per lm (vedi l'help)
# [ se non trovi ~ nella tastiera, se non hai sottomano questo documento da cui
# copiarlo, … puoi usare help(tilde) e copiarlo dalla pagina che si apre ]
 # la figura a destra è stata ottenuta con:
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="");points(x,y)
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod)
# posso cambiare dimensioni/forma/colore dei punti con opzioni
# a points
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod$coefficients); points(x,y, pch=".")
# il primo grafico è stato ottenuto con le righe precedenti, il
# secondo modificando, oltre al colore, le dimensioni dei punti con cex
points(x,y, pch=".", cex=2, col="green")
# il terzo modificamdo la forma dei punti (a pch si dà un numero tra 21 e 25)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="");points(x,y,pch=25)
# la figura a destra è stata ottenuta con:
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="");points(x,y)
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod)
# posso cambiare dimensioni/forma/colore dei punti con opzioni
# a points
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod$coefficients); points(x,y, pch=".")
# il primo grafico è stato ottenuto con le righe precedenti, il
# secondo modificando, oltre al colore, le dimensioni dei punti con cex
points(x,y, pch=".", cex=2, col="green")
# il terzo modificamdo la forma dei punti (a pch si dà un numero tra 21 e 25)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="");points(x,y,pch=25)
 #
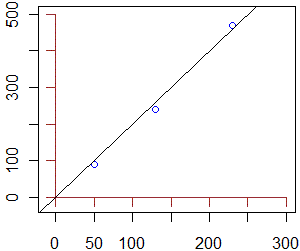
# se disponiamo di tre coppie di dati tra due grandezze x ed y che
# sappiamo essere legate da una relazione y = kx e non conosciamo la
# precisione dei dati (altrimenti procederemmo così), possiamo trovare
# la retta di regressione vincolata a passare per (0,0)
x<-c(50,130,230); y <-c(90,240,470)
x1 <- -10; x2 <- 300; y1 <- -20; y2 <- 500
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
points(x,y,col="blue")
k <- mean(x*y)/mean(x^2); k; abline(0,k)
[1] 1.988935
# Ma posso procedere direttamente anche lm(y ~ x - 1) (lm con aggiunto "-1"):
lm(y ~ x-1)$coefficients
x
1.988935
#
# se disponiamo di tre coppie di dati tra due grandezze x ed y che
# sappiamo essere legate da una relazione y = kx e non conosciamo la
# precisione dei dati (altrimenti procederemmo così), possiamo trovare
# la retta di regressione vincolata a passare per (0,0)
x<-c(50,130,230); y <-c(90,240,470)
x1 <- -10; x2 <- 300; y1 <- -20; y2 <- 500
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
points(x,y,col="blue")
k <- mean(x*y)/mean(x^2); k; abline(0,k)
[1] 1.988935
# Ma posso procedere direttamente anche lm(y ~ x - 1) (lm con aggiunto "-1"):
lm(y ~ x-1)$coefficients
x
1.988935
 #
# Ecco come calcolare la covarianza, e come ottenerne la correlazione:
cov(x,y)
# 78.39035
cov(x,y)/sd(x)/sd(y); cor(x,y)
# 0.7826331 0.7826331
#
# Altri esempi reperibili qui:
#
# Ecco come calcolare la covarianza, e come ottenerne la correlazione:
cov(x,y)
# 78.39035
cov(x,y)/sd(x)/sd(y); cor(x,y)
# 0.7826331 0.7826331
#
# Altri esempi reperibili qui:


 | QQ-plot |
#
# Altri reperibili qui (componenti principali: prcomp)
 #
# il test χ2 (e livelli di confidenza): vedi qui
#
# il test t di Student: vedi qui
#
# Parabola che "meglio" approssima i punti seguenti (vedi qui)
# x <- c(-5,-2.6,-0.4,2.2,3)
# y <- c(-1.3,-2.6,-1,4,5.4)
#
# il test χ2 (e livelli di confidenza): vedi qui
#
# il test t di Student: vedi qui
#
# Parabola che "meglio" approssima i punti seguenti (vedi qui)
# x <- c(-5,-2.6,-0.4,2.2,3)
# y <- c(-1.3,-2.6,-1,4,5.4)
 #
# Altri (tabelle di dati classificati: tabelle di contingenza - vedi) sono
# reperibili qui (prop.table, colSums, rowSums, mosaicplot), qui:
#
# Altri (tabelle di dati classificati: tabelle di contingenza - vedi) sono
# reperibili qui (prop.table, colSums, rowSums, mosaicplot), qui:

 # e qui:
# e qui:
DONNE
<18 <21 <25 <30 <35 <40 <45 <50 <55 <60 <65 <70 ≥70
<18 5 1 0 0 0 0 0 0 0 0 0 0 0
U <21 61 63 26 2 0 1 0 0 0 0 1 0 0
O <25 100 416 577 148 16 2 0 0 0 0 1 1 0
M <30 55 306 916 691 85 18 4 1 1 0 0 0 0
I <35 6 38 153 231 116 48 9 1 1 3 0 0 0
N <40 1 11 34 85 67 40 27 10 4 0 0 0 0
I <45 0 0 4 13 26 28 24 20 9 1 0 0 0
<50 0 0 1 8 14 20 32 27 20 5 0 0 0
<55 0 0 2 2 8 11 30 25 26 9 4 1 0
<60 0 0 0 1 2 5 14 22 27 11 6 0 1
<65 0 0 1 0 1 3 6 17 21 17 16 6 1
<70 0 0 0 0 0 1 1 3 11 10 13 12 4
≥70 0 0 0 0 0 0 1 0 3 3 6 7 6 |
# Gaussiane, o distribuzioni normali (dnorm indica la densità, pnorm la
# funzione di ripartizione, rnorm genera uscite casuali)
y <- rnorm(n=10000,mean=180,sd=6)
mean(y)
[1] 180.0364
y <- rnorm(n=10000,mean=180,sd=6)
mean(y)
[1] 179.926
sd(y)
[1] 5.996126
hist(y,20)
 # la corrispondente gaussiana e la sua ripartizione
z <- function(x) dnorm(x,mean=180,sd=6); plot(z,155,205)
t <- function(x) pnorm(x,mean=180,sd=6); plot(t,155,205)
# la corrispondente gaussiana e la sua ripartizione
z <- function(x) dnorm(x,mean=180,sd=6); plot(z,155,205)
t <- function(x) pnorm(x,mean=180,sd=6); plot(t,155,205)
 # vedi qui per la funzione degli errori erf
#
# gaussiana in forma esplicita
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,m-s,m+s); integrate(f,m-3*s,m+3*s); integrate(f,-Inf,Inf)
0.6826895 with absolute error < 7.6e-15
0.9973002 with absolute error < 9.3e-07
1 with absolute error < 7.6e-06
#
# una distribuzione esponenziale dove rate è 1/m, dexp(x) è rate*exp(-rate*x)
# ("rate" in inglese significa velocità; m infatti esprime il tempo medio nel
# caso in cui la legge rappresenti il tempo tra l'arrivo di due telefonate o
# di due auto ad un semaforo)
curve(dexp(x, rate = 5), col="red", xlab="", ylab = "densitÓ", from = 0, to = 2)
# vedi qui per la funzione degli errori erf
#
# gaussiana in forma esplicita
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,m-s,m+s); integrate(f,m-3*s,m+3*s); integrate(f,-Inf,Inf)
0.6826895 with absolute error < 7.6e-15
0.9973002 with absolute error < 9.3e-07
1 with absolute error < 7.6e-06
#
# una distribuzione esponenziale dove rate è 1/m, dexp(x) è rate*exp(-rate*x)
# ("rate" in inglese significa velocità; m infatti esprime il tempo medio nel
# caso in cui la legge rappresenti il tempo tra l'arrivo di due telefonate o
# di due auto ad un semaforo)
curve(dexp(x, rate = 5), col="red", xlab="", ylab = "densitÓ", from = 0, to = 2)
 # una esponenziale in forma esplicita
h<- function(x) exp(-x*2)*2; integrate(h,0,1);integrate(h,1,Inf);integrate(h,0,Inf)
0.8646647 with absolute error < 9.6e-15
0.1353353 with absolute error < 2.1e-05
1 with absolute error < 5e-07
#
# la distribuzione binomiale di dato ordine e data probabilità
# di successo nella singola prova
plot(0:10,dbinom(0:10,10, 1/2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.8),type="h", lwd=3, xlab="", ylab="")
# una esponenziale in forma esplicita
h<- function(x) exp(-x*2)*2; integrate(h,0,1);integrate(h,1,Inf);integrate(h,0,Inf)
0.8646647 with absolute error < 9.6e-15
0.1353353 with absolute error < 2.1e-05
1 with absolute error < 5e-07
#
# la distribuzione binomiale di dato ordine e data probabilità
# di successo nella singola prova
plot(0:10,dbinom(0:10,10, 1/2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.8),type="h", lwd=3, xlab="", ylab="")
 #
# Per studiare, più in generale, le distribuzioni multinomiali, si usa dmultinom: vedi
#
# Una funzione densità bivariata (vedi qui)
#
# Per studiare, più in generale, le distribuzioni multinomiali, si usa dmultinom: vedi
#
# Una funzione densità bivariata (vedi qui)
 # Problema:
# Sappiamo che il 12% della popolazione mondiale e' mancina.
# Qual è la probabilita' che in un campione casuale di 100 persone il
# numero di mancini sia compreso tra 10 e 14 (estremi inclusi)?
sum(dbinom(10:14, 100, 0.12)))
[1] 0.5583493
# alternativa: Pr(10 <= X1+X2+...+X100 <= 14) con Xi = 1/0 a seconda che
# i-ma persona sia o no mancina; ha andamento approssimativamente normale,
# con media 12%*100 = 12 e varianza pari a 100 volte la varianza degli Xi:
# 100*0.12*(1-0.12) = 10.56
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,9.5,14.5)
0.5582977 with absolute error < 6.2e-15
#
# Tre diversi grafici di una poissoniana
k <- 0:20
p <- dpois(k, lambda = 5)
plot(k, p, type = "h", xlab="", ylab="")
plot(k, p, main = "Poisson")
plot(k, p, type = "h", lwd = 6, xlab="", ylab="")
# Problema:
# Sappiamo che il 12% della popolazione mondiale e' mancina.
# Qual è la probabilita' che in un campione casuale di 100 persone il
# numero di mancini sia compreso tra 10 e 14 (estremi inclusi)?
sum(dbinom(10:14, 100, 0.12)))
[1] 0.5583493
# alternativa: Pr(10 <= X1+X2+...+X100 <= 14) con Xi = 1/0 a seconda che
# i-ma persona sia o no mancina; ha andamento approssimativamente normale,
# con media 12%*100 = 12 e varianza pari a 100 volte la varianza degli Xi:
# 100*0.12*(1-0.12) = 10.56
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,9.5,14.5)
0.5582977 with absolute error < 6.2e-15
#
# Tre diversi grafici di una poissoniana
k <- 0:20
p <- dpois(k, lambda = 5)
plot(k, p, type = "h", xlab="", ylab="")
plot(k, p, main = "Poisson")
plot(k, p, type = "h", lwd = 6, xlab="", ylab="")
 # modi per ottenerne i valori:
p
[1] 6.737947e-03 3.368973e-02 8.422434e-02 1.403739e-01 1.754674e-01
[6] 1.754674e-01 1.462228e-01 1.044449e-01 6.527804e-02 3.626558e-02
[11] 1.813279e-02 8.242177e-03 3.434240e-03 1.320862e-03 4.717363e-04
[16] 1.572454e-04 4.913920e-05 1.445271e-05 4.014640e-06 1.056484e-06
[21] 2.641211e-07
p[5]
[1] 0.1754674
p[2]+p[3]+p[4]
[1] 0.2582880
s<-0; for (i in 2:4) s <- s+p[i]; s
[1] 0.2582880
#
# Per varie distribuzioni aziona:
help(Distributions)
# - è possibile avere sia la legge teorica ("d..." densità,
# "p..." distribuzione) che la generazione sperimentale con runif ("r...").
# Abbiamo visto la binomiale ("...binom"), la poissoniana ("...pois"),
# la normale ("...norm"), la esponenziale ("...exp"). Esempio
plot(0:6,dbinom(0:6,6, 1/8),type="h", lwd=6);
dev.new(); plot(0:6,pbinom(0:6,6, 1/8),type="h", lwd=6)
# modi per ottenerne i valori:
p
[1] 6.737947e-03 3.368973e-02 8.422434e-02 1.403739e-01 1.754674e-01
[6] 1.754674e-01 1.462228e-01 1.044449e-01 6.527804e-02 3.626558e-02
[11] 1.813279e-02 8.242177e-03 3.434240e-03 1.320862e-03 4.717363e-04
[16] 1.572454e-04 4.913920e-05 1.445271e-05 4.014640e-06 1.056484e-06
[21] 2.641211e-07
p[5]
[1] 0.1754674
p[2]+p[3]+p[4]
[1] 0.2582880
s<-0; for (i in 2:4) s <- s+p[i]; s
[1] 0.2582880
#
# Per varie distribuzioni aziona:
help(Distributions)
# - è possibile avere sia la legge teorica ("d..." densità,
# "p..." distribuzione) che la generazione sperimentale con runif ("r...").
# Abbiamo visto la binomiale ("...binom"), la poissoniana ("...pois"),
# la normale ("...norm"), la esponenziale ("...exp"). Esempio
plot(0:6,dbinom(0:6,6, 1/8),type="h", lwd=6);
dev.new(); plot(0:6,pbinom(0:6,6, 1/8),type="h", lwd=6)
 # rbinom simula il fenomeno; ecco come ottenere 20 uscite sperimentali
rbinom(20,6, 1/8)
[1] 1 0 0 3 0 0 0 1 0 1 0 1 2 0 1 0 0 1 0 1
# per ottenere l'istogramma devo, ora, classificare le uscite in
# opportuni intervalli
hist(rbinom(50,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
hist(rbinom(5000,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
# rbinom simula il fenomeno; ecco come ottenere 20 uscite sperimentali
rbinom(20,6, 1/8)
[1] 1 0 0 3 0 0 0 1 0 1 0 1 2 0 1 0 0 1 0 1
# per ottenere l'istogramma devo, ora, classificare le uscite in
# opportuni intervalli
hist(rbinom(50,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
hist(rbinom(5000,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
 # Vedi qui per accedere a librerie esterne, ad esempio per caricare
# particolari distribuzioni
#
# Ecco come raggruppare più grafici:
# mar: vettore c(bottom, left, top, right); da' il numero di linee di
# margine per i quattro lati (l'assenza equivale a c(5, 4, 4, 2) + 0.1)
# mfrow: vettore c(m, n); le figure sono tracciate in una tabella di
# m×n: m righe (row) e n colonne (mf sta per "formato dei margini")
vendite <- c(0.12, 0.3, 0.26, 0.16, 0.04, 0.12)
names(vendite) <- LETTERS[1:length(vendite)]
vendite
A B C D E F
0.12 0.30 0.26 0.16 0.04 0.12
par(mfrow=c(2,2), mar=c(3,3,2,1))
barplot(vendite)
pie(vendite)
pie(vendite, col = c("red","purple","blue","green","yellow","orange"))
dotchart(vendite)
# Vedi qui per accedere a librerie esterne, ad esempio per caricare
# particolari distribuzioni
#
# Ecco come raggruppare più grafici:
# mar: vettore c(bottom, left, top, right); da' il numero di linee di
# margine per i quattro lati (l'assenza equivale a c(5, 4, 4, 2) + 0.1)
# mfrow: vettore c(m, n); le figure sono tracciate in una tabella di
# m×n: m righe (row) e n colonne (mf sta per "formato dei margini")
vendite <- c(0.12, 0.3, 0.26, 0.16, 0.04, 0.12)
names(vendite) <- LETTERS[1:length(vendite)]
vendite
A B C D E F
0.12 0.30 0.26 0.16 0.04 0.12
par(mfrow=c(2,2), mar=c(3,3,2,1))
barplot(vendite)
pie(vendite)
pie(vendite, col = c("red","purple","blue","green","yellow","orange"))
dotchart(vendite)
 # ritorniamo alla modalità standard:
par(mfrow=c(1,1))
barplot(vendite)
# ritorniamo alla modalità standard:
par(mfrow=c(1,1))
barplot(vendite)
 #
# Coi comandi precedenti si possono anche affiancare grafici e testo
# in un'unica finestra:
par(mfrow=c(1,2), mar=c(3,2,2,1))
# parte sinistra
f <- function(x) x^2
plot(f,-2,2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# parte destra
plot(c(0,100),c(0,100),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
# una griglia per posizionare il testo (poi posso cancellare la riga)
abline(v=axTicks(1), h=axTicks(2), col="yellow",lty=3)
text(20,100,"Ecco la prova",family="mono",adj=0,cex=2,font=2)
text(-3,90,"di un grafico e un testo",family="mono",adj=0,cex=1.3,font=2)
text(0,80,"ottenuti con R",family="mono",adj=0,cex=1.7,font=2,col="blue")
text(0,25,"Vedi com'Ŕ stata gestita la pag.",family="mono",adj=0,cex=1,font=4)
text(50,10,"Ciao",cex=3,col="red")
#
# Coi comandi precedenti si possono anche affiancare grafici e testo
# in un'unica finestra:
par(mfrow=c(1,2), mar=c(3,2,2,1))
# parte sinistra
f <- function(x) x^2
plot(f,-2,2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# parte destra
plot(c(0,100),c(0,100),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
# una griglia per posizionare il testo (poi posso cancellare la riga)
abline(v=axTicks(1), h=axTicks(2), col="yellow",lty=3)
text(20,100,"Ecco la prova",family="mono",adj=0,cex=2,font=2)
text(-3,90,"di un grafico e un testo",family="mono",adj=0,cex=1.3,font=2)
text(0,80,"ottenuti con R",family="mono",adj=0,cex=1.7,font=2,col="blue")
text(0,25,"Vedi com'Ŕ stata gestita la pag.",family="mono",adj=0,cex=1,font=4)
text(50,10,"Ciao",cex=3,col="red")
 # Si possono visualizzare testi senza introdurli riga per riga: vedi
# Si possono visualizzare testi senza introdurli riga per riga: vedi
 #
# edit() apre una finestra in cui si possono scrivere comandi
# e poi eseguire, copiare, ... usando il menu che si apre col
# pulsante del mouse
#
# Il comando class classifica comandi e oggetti via via definiti.
# Può essere utile per ricordare definizioni introdotte o per capire
# alcuni aspetti del funzionamento di R. Qualche esempio:
A <- 155.2516; class(A); f <- function(x) x^2; class(f)
[1] "numeric"
[1] "function"
class(print); class(1>2); class("f")
[1] "function"
[1] "logical"
[1] "character"
class(c(f, 1>2, 3)); class(c(1,2,-5))
[1] "list"
[1] "numeric"
class(text(-2,-4,"x")); class(text)
[1] "NULL"
[1] "function"
class(hist(c(1,3,4,5,0,2,7))); class(hist)
[1] "histogram"
[1] "function"
class(array(c(1,3,4,5),dim=c(2,2))); class(array)
[1] "matrix"
[1] "function"
class(D(expression(x^4),"x")); class(expression(x^4)); class(2^4)
[1] "call"
[1] "expression"
[1] "numeric"
class(integrate(f,0,1)); class(integrate(f,0,1)$value)
[1] "integrate"
[1] "numeric"
#
# Come si è già osservato, col comando write una sequenza di dati può essere salvata
# in un file sul proprio computer. Suppongo di avere caricato da rete una tabella:
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.txt",n=11)
[1] "# battiti prima di eventuale corsa di 1 min"
[2] "# battiti dopo"
[3] "# fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[4] "# fumatore (1 si`;0 no)"
[5] "# sesso (1 M; 2 F)"
[6] "# altezza"
[7] "# peso"
[8] "# attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[9] " BatPrima BatDopo Corsa Fumo Sesso Alt Peso Fis"
[10] "01 64 88 1 0 1 168 64 2"
[11] "02 58 70 1 0 1 183 66 2"
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.txt",header=TRUE)
str(dati)
'data.frame': 92 obs. of 8 variables:
$ BatPrima: int 64 58 62 66 64 74 84 68 62 76 ...
$ BatDopo : int 88 70 76 78 80 84 84 72 75 118 ...
$ Corsa : int 1 1 1 1 1 1 1 1 1 1 ...
$ Fumo : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sesso : int 1 1 1 1 1 1 1 1 1 1 ...
$ Alt : int 168 183 186 184 176 184 184 188 184 181 ...
$ Peso : int 64 66 73 86 70 75 68 86 88 63 ...
$ Fis : int 2 2 3 1 2 1 3 2 2 2 ...
# Voglio estrarre le altezze:
str(dati$Alt)
int [1:92] 168 183 186 184 176 184 184 188 184 181 ...
# Le metto nel file "altezze.txt" del mio computer (non metto percorso: il file
# viene messo nella cartella di default, in genere "documenti"; altrimenti metto
# il percorso)
write(dati$Alt, "altezze.txt")
# I dati vengono inseriti seprati da uno spazio bianco o un ACapo, con:
write(dati$Alt, "altezze.txt", ncolumns=1)
# essi vengono scritti in un'unica colonna, uno sotto l'altro.
# A questo punto, anche dopo, anche non in rete, posso esaminare il file:
dati <- scan("altezze.txt")
Read 92 items
summary(dati)
Min. 1st Qu. Median Mean 3rd Qu. Max.
154.0 167.8 175.0 174.4 183.0 190.0
#
#
# edit() apre una finestra in cui si possono scrivere comandi
# e poi eseguire, copiare, ... usando il menu che si apre col
# pulsante del mouse
#
# Il comando class classifica comandi e oggetti via via definiti.
# Può essere utile per ricordare definizioni introdotte o per capire
# alcuni aspetti del funzionamento di R. Qualche esempio:
A <- 155.2516; class(A); f <- function(x) x^2; class(f)
[1] "numeric"
[1] "function"
class(print); class(1>2); class("f")
[1] "function"
[1] "logical"
[1] "character"
class(c(f, 1>2, 3)); class(c(1,2,-5))
[1] "list"
[1] "numeric"
class(text(-2,-4,"x")); class(text)
[1] "NULL"
[1] "function"
class(hist(c(1,3,4,5,0,2,7))); class(hist)
[1] "histogram"
[1] "function"
class(array(c(1,3,4,5),dim=c(2,2))); class(array)
[1] "matrix"
[1] "function"
class(D(expression(x^4),"x")); class(expression(x^4)); class(2^4)
[1] "call"
[1] "expression"
[1] "numeric"
class(integrate(f,0,1)); class(integrate(f,0,1)$value)
[1] "integrate"
[1] "numeric"
#
# Come si è già osservato, col comando write una sequenza di dati può essere salvata
# in un file sul proprio computer. Suppongo di avere caricato da rete una tabella:
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.txt",n=11)
[1] "# battiti prima di eventuale corsa di 1 min"
[2] "# battiti dopo"
[3] "# fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[4] "# fumatore (1 si`;0 no)"
[5] "# sesso (1 M; 2 F)"
[6] "# altezza"
[7] "# peso"
[8] "# attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[9] " BatPrima BatDopo Corsa Fumo Sesso Alt Peso Fis"
[10] "01 64 88 1 0 1 168 64 2"
[11] "02 58 70 1 0 1 183 66 2"
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.txt",header=TRUE)
str(dati)
'data.frame': 92 obs. of 8 variables:
$ BatPrima: int 64 58 62 66 64 74 84 68 62 76 ...
$ BatDopo : int 88 70 76 78 80 84 84 72 75 118 ...
$ Corsa : int 1 1 1 1 1 1 1 1 1 1 ...
$ Fumo : int 0 0 1 1 0 0 0 0 0 0 ...
$ Sesso : int 1 1 1 1 1 1 1 1 1 1 ...
$ Alt : int 168 183 186 184 176 184 184 188 184 181 ...
$ Peso : int 64 66 73 86 70 75 68 86 88 63 ...
$ Fis : int 2 2 3 1 2 1 3 2 2 2 ...
# Voglio estrarre le altezze:
str(dati$Alt)
int [1:92] 168 183 186 184 176 184 184 188 184 181 ...
# Le metto nel file "altezze.txt" del mio computer (non metto percorso: il file
# viene messo nella cartella di default, in genere "documenti"; altrimenti metto
# il percorso)
write(dati$Alt, "altezze.txt")
# I dati vengono inseriti seprati da uno spazio bianco o un ACapo, con:
write(dati$Alt, "altezze.txt", ncolumns=1)
# essi vengono scritti in un'unica colonna, uno sotto l'altro.
# A questo punto, anche dopo, anche non in rete, posso esaminare il file:
dati <- scan("altezze.txt")
Read 92 items
summary(dati)
Min. 1st Qu. Median Mean 3rd Qu. Max.
154.0 167.8 175.0 174.4 183.0 190.0
#
 #
# Ecco alcune prime elaborazioni:
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# ecco una rapida analisi delle colonne
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# come analizzare i dati della prima colonna
a <- t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# e quelli della sesta riga
b <- t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# gli stessi dati organizzati in una tabella 3×8
u <- array(z,dim=c(3,8)); u
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 4 7 0 3 6 9 2
[2,] 2 5 8 1 4 7 0 3
[3,] 3 6 9 2 5 8 1 4
#
# Conviene analizzare tabelle di dati gia' memorizzati come file distinti; se
# sei in rete puoi analizzare direttamente il file seguente, che puoi
# richiamare dal browser mettendo il nome (usando "/", non "\")
# http://macosa.dima.unige.it/sosta/dati3.txt come argomento di
# read.table o puoi copiare da qui sotto (dalla riga "peso altezza ..."
# alla riga "4 60 170 m"), incollare in un file di testo a cui dare un
# nome (ad es. lo stesso, dati3.txt), scegliere col comando Change Dir
# (dal menù File) la cartella del computer in cui lo hai messo (che può
# essere esaminata col comando dir() - solo dir ne dà il percorso) e poi
# mettere dati <- read.table("dati3.txt") invece di:
dati <- read.table("http://macosa.dima.unige.it/sosta/dati3.txt")
# se azionassi dati otterrei:
peso altezza sesso
1 65 184 m
2 71 192 f
3 59 163 f
4 60 170 m
# [ in ogni caso (come spiegato più avanti) conviene esaminare un
# po' di righe del file con readLines(..., n=...) ]
# [Nota: dir() stampa tutto il contenuto della cartella (directory) corrente,
# dir(..) quello della cartella soprastante, dir(../..) quello di quella che
# la contiene, ...; usando in modo analogo list.dirs si ha la stampa delle
# sole cartelle, non dei file]
# In questo caso è facile esaminare le dimensioni della tabella, ma in
# generale conviene (prima di una sua eventuale stampa, se non è troppo
# lunga) usare il comando dim per sapere quante sono righe e colonne:
dim(dati)
[1] 4 3
summary(dati)
peso altezza sesso
Min. :59.00 Min. :163.0 f:2
1st Qu.:59.75 1st Qu.:168.2 m:2
Median :62.50 Median :177.0
Mean :63.75 Mean :177.2
3rd Qu.:66.50 3rd Qu.:186.0
Max. :71.00 Max. :192.0
# per estrarre una singola variabile dalla tabella puoi usare $:
a <- dati$peso
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
59.00 59.75 62.50 63.75 66.50 71.00
#
# Oltre che con read.table, abbiamo visto come con read.csv2 si possono
# leggere dati da una tabella, quando in particolare sono in un foglio
# di calcolo. Analogamente con write.csv e write.csv2 si può copiare una
# tabella di dati in un foglio di calcolo, usando "." o "," per separare
# parte intera e parte frazionaria. Ad es. i dati precedenti con il
# seguente comando vengono messi nel file tabel.csv
write.csv(dati,file = "tabel.csv")
#
# Questo è il modo standard in cui sono memorizzati i dati; ma
# il programma è in grado di analizzare dati regitrstati quasi in
# ogni modo; vediamo un esempio, in cui usiamo i comandi readLines
# per analizzare i file e read.table (o read.delim) per caricarli:
# [puoi azionare help(read.table) per dettagli]
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab")
[1] "'tabella (indagine su studenti di un corso universitario - dati tratti da"
[2] "'un esempio riportato nel manuale di MiniTab)"
[3] "'a: battiti prima di eventuale corsa di 1 min"
[4] "'b: battiti dopo"
[5] "'c: fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[6] "'d: fumatore (1 si`;0 no)"
[7] "'e: sesso (1 M; 2 F)"
[8] "'f: altezza"
[9] "'g: peso"
[10] "'h: attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[11] " 64; 88;1;0;1;168;64;2"
...
# Ma conviene, per non riempire lo schermo e per vedere solo come sono
# introdotti i dati, delimitare le righe da vedere con n =
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab",n=11)
#
# nel comando metto header=FALSE per indicare che non c'è una
# intestazione delle colonne, skip=10 per indicare le righe da saltare,
# sep=";" per specificare qual è l'elemento di separazione tra i dati
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
# ovvero
dati <- read.delim("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
dati
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
4 66 78 1 1 1 184 86 1
5 64 80 1 0 1 176 70 2
6 74 84 1 0 1 184 75 1
7 84 84 1 0 1 184 68 3
...
89 78 80 0 0 2 173 60 1
90 68 68 0 0 2 159 50 2
91 86 84 0 0 2 171 68 3
92 76 76 0 0 2 156 49 2
# Un modo comodo (e non ingombrante) per capire che cosa si sta
# analizzando è usare il comando str (struttura):
str(dati)
'data.frame': 92 obs. of 8 variables:
$ V1: int 64 58 62 66 64 74 84 68 62 76 ...
$ V2: int 88 70 76 78 80 84 84 72 75 118 ...
$ V3: int 1 1 1 1 1 1 1 1 1 1 ...
$ V4: int 0 0 1 1 0 0 0 0 0 0 ...
$ V5: int 1 1 1 1 1 1 1 1 1 1 ...
$ V6: int 168 183 186 184 176 184 184 188 184 181 ...
$ V7: int 64 66 73 86 70 75 68 86 88 63 ...
$ V8: int 2 2 3 1 2 1 3 2 2 2 ...
summary(dati)
V1 V2 V3 V4
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V5 V6 V7 V8
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# le colonne, in assenza di intestazioni, sono intestate automaticamente
# (dalle prime righe del file capisco che V1 sono i battiti prima
# della corsa, ..., V6 sono le altezze, ...)
a1 <- dati$V1; summary(a1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(a1)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
hist(a1,right=FALSE)
hist(a1,seq(40,100,10), right=FALSE)
#
# Ecco alcune prime elaborazioni:
length(t); colMeans(t);rowMeans(t)
[1] 24
[1] 3.500000 4.500000 5.500000 3.166667
[1] 5.0 3.5 4.5 3.0 4.0 5.0
#
# ecco una rapida analisi delle colonne
summary(t)
V1 V2 V3 V4
Min. :1.00 Min. :0.00 Min. :3.00 Min. :0.000
1st Qu.:2.25 1st Qu.:1.25 1st Qu.:4.25 1st Qu.:1.250
Median :3.50 Median :4.50 Median :5.50 Median :2.500
Mean :3.50 Mean :4.50 Mean :5.50 Mean :3.167
3rd Qu.:4.75 3rd Qu.:7.75 3rd Qu.:6.75 3rd Qu.:3.750
Max. :6.00 Max. :9.00 Max. :8.00 Max. :9.000
# come analizzare i dati della prima colonna
a <- t[,1]; a
[1] 1 2 3 4 5 6
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.00 2.25 3.50 3.50 4.75 6.00
# e quelli della sesta riga
b <- t[6,]; b; summary(b)
[1] 6 2 8 4
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.0 3.5 5.0 5.0 6.5 8.0
# gli stessi dati organizzati in una tabella 3×8
u <- array(z,dim=c(3,8)); u
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 4 7 0 3 6 9 2
[2,] 2 5 8 1 4 7 0 3
[3,] 3 6 9 2 5 8 1 4
#
# Conviene analizzare tabelle di dati gia' memorizzati come file distinti; se
# sei in rete puoi analizzare direttamente il file seguente, che puoi
# richiamare dal browser mettendo il nome (usando "/", non "\")
# http://macosa.dima.unige.it/sosta/dati3.txt come argomento di
# read.table o puoi copiare da qui sotto (dalla riga "peso altezza ..."
# alla riga "4 60 170 m"), incollare in un file di testo a cui dare un
# nome (ad es. lo stesso, dati3.txt), scegliere col comando Change Dir
# (dal menù File) la cartella del computer in cui lo hai messo (che può
# essere esaminata col comando dir() - solo dir ne dà il percorso) e poi
# mettere dati <- read.table("dati3.txt") invece di:
dati <- read.table("http://macosa.dima.unige.it/sosta/dati3.txt")
# se azionassi dati otterrei:
peso altezza sesso
1 65 184 m
2 71 192 f
3 59 163 f
4 60 170 m
# [ in ogni caso (come spiegato più avanti) conviene esaminare un
# po' di righe del file con readLines(..., n=...) ]
# [Nota: dir() stampa tutto il contenuto della cartella (directory) corrente,
# dir(..) quello della cartella soprastante, dir(../..) quello di quella che
# la contiene, ...; usando in modo analogo list.dirs si ha la stampa delle
# sole cartelle, non dei file]
# In questo caso è facile esaminare le dimensioni della tabella, ma in
# generale conviene (prima di una sua eventuale stampa, se non è troppo
# lunga) usare il comando dim per sapere quante sono righe e colonne:
dim(dati)
[1] 4 3
summary(dati)
peso altezza sesso
Min. :59.00 Min. :163.0 f:2
1st Qu.:59.75 1st Qu.:168.2 m:2
Median :62.50 Median :177.0
Mean :63.75 Mean :177.2
3rd Qu.:66.50 3rd Qu.:186.0
Max. :71.00 Max. :192.0
# per estrarre una singola variabile dalla tabella puoi usare $:
a <- dati$peso
summary(a)
Min. 1st Qu. Median Mean 3rd Qu. Max.
59.00 59.75 62.50 63.75 66.50 71.00
#
# Oltre che con read.table, abbiamo visto come con read.csv2 si possono
# leggere dati da una tabella, quando in particolare sono in un foglio
# di calcolo. Analogamente con write.csv e write.csv2 si può copiare una
# tabella di dati in un foglio di calcolo, usando "." o "," per separare
# parte intera e parte frazionaria. Ad es. i dati precedenti con il
# seguente comando vengono messi nel file tabel.csv
write.csv(dati,file = "tabel.csv")
#
# Questo è il modo standard in cui sono memorizzati i dati; ma
# il programma è in grado di analizzare dati regitrstati quasi in
# ogni modo; vediamo un esempio, in cui usiamo i comandi readLines
# per analizzare i file e read.table (o read.delim) per caricarli:
# [puoi azionare help(read.table) per dettagli]
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab")
[1] "'tabella (indagine su studenti di un corso universitario - dati tratti da"
[2] "'un esempio riportato nel manuale di MiniTab)"
[3] "'a: battiti prima di eventuale corsa di 1 min"
[4] "'b: battiti dopo"
[5] "'c: fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta)"
[6] "'d: fumatore (1 si`;0 no)"
[7] "'e: sesso (1 M; 2 F)"
[8] "'f: altezza"
[9] "'g: peso"
[10] "'h: attivita` fisica (0 nulla;1 poca;2 media; 3 molta)"
[11] " 64; 88;1;0;1;168;64;2"
...
# Ma conviene, per non riempire lo schermo e per vedere solo come sono
# introdotti i dati, delimitare le righe da vedere con n =
readLines("http://macosa.dima.unige.it/om/prg/stf/battito.tab",n=11)
#
# nel comando metto header=FALSE per indicare che non c'è una
# intestazione delle colonne, skip=10 per indicare le righe da saltare,
# sep=";" per specificare qual è l'elemento di separazione tra i dati
dati <- read.table("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
# ovvero
dati <- read.delim("http://macosa.dima.unige.it/om/prg/stf/battito.tab",header=FALSE,skip=10,sep =";")
dati
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
4 66 78 1 1 1 184 86 1
5 64 80 1 0 1 176 70 2
6 74 84 1 0 1 184 75 1
7 84 84 1 0 1 184 68 3
...
89 78 80 0 0 2 173 60 1
90 68 68 0 0 2 159 50 2
91 86 84 0 0 2 171 68 3
92 76 76 0 0 2 156 49 2
# Un modo comodo (e non ingombrante) per capire che cosa si sta
# analizzando è usare il comando str (struttura):
str(dati)
'data.frame': 92 obs. of 8 variables:
$ V1: int 64 58 62 66 64 74 84 68 62 76 ...
$ V2: int 88 70 76 78 80 84 84 72 75 118 ...
$ V3: int 1 1 1 1 1 1 1 1 1 1 ...
$ V4: int 0 0 1 1 0 0 0 0 0 0 ...
$ V5: int 1 1 1 1 1 1 1 1 1 1 ...
$ V6: int 168 183 186 184 176 184 184 188 184 181 ...
$ V7: int 64 66 73 86 70 75 68 86 88 63 ...
$ V8: int 2 2 3 1 2 1 3 2 2 2 ...
summary(dati)
V1 V2 V3 V4
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
V5 V6 V7 V8
Min. :1.000 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.000 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.000 Median :175.0 Median :66.00 Median :2.000
Mean :1.380 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.000 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.000 Max. :190.0 Max. :97.00 Max. :3.000
# le colonne, in assenza di intestazioni, sono intestate automaticamente
# (dalle prime righe del file capisco che V1 sono i battiti prima
# della corsa, ..., V6 sono le altezze, ...)
a1 <- dati$V1; summary(a1)
Min. 1st Qu. Median Mean 3rd Qu. Max.
48.00 64.00 71.00 72.87 80.00 100.00
stem(a1)
The decimal point is 1 digit(s) to the right of the |
4 | 8
5 | 44888
6 | 0000122222222244446666688888888888
7 | 000000222222444446666688888
8 | 000222444467888
9 | 000022466
10 | 0
hist(a1,right=FALSE)
hist(a1,seq(40,100,10), right=FALSE)
 # Come sovrapporre gli istogrammi di due sottopopolazioni.
# Vedi qui per l'es. seguente (altezze maschi e femmine)
# Come sovrapporre gli istogrammi di due sottopopolazioni.
# Vedi qui per l'es. seguente (altezze maschi e femmine)
 # Come estrarre/togliere righe o colonne da una tabella
# Vedi qui per un esempio.
# Come unire tabelle. Vedi qui per un esempio.
#
# i coefficienti di correlazione tra le diverse variabili
# [ vedi qui per come associare ad essi un intervallo di indeterminazione ]
cor(dati)
V1 V2 V3 V4
V1 1.00000000 0.61619572 0.052277524 0.12870465
V2 0.61619572 1.00000000 0.576816142 0.04585426
V3 0.05227752 0.57681614 1.000000000 0.06558148
V4 0.12870465 0.04585426 0.065581483 1.00000000
V5 0.28539261 0.30947898 -0.106766917 -0.12904743
V6 -0.21102575 -0.15326188 0.223595030 0.04278398
V7 -0.20322133 -0.16637381 0.224024008 0.20061688
V8 -0.06256772 -0.14110121 0.007323575 -0.12020183
V5 V6 V7 V8
V1 0.2853926 -0.21102575 -0.203221327 -0.062567716
V2 0.3094790 -0.15326188 -0.166373807 -0.141101211
V3 -0.1067669 0.22359503 0.224024008 0.007323575
V4 -0.1290474 0.04278398 0.200616884 -0.120201834
V5 1.0000000 -0.70902885 -0.710227077 -0.104971238
V6 -0.7090288 1.00000000 0.782633130 0.089299812
V7 -0.7102271 0.78263313 1.000000000 -0.004037995
V8 -0.1049712 0.08929981 -0.004037995 1.000000000
# Per avere meno (o più) cifre possiamo usare print e round
print(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V2 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V3 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V4 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V5 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.7090 -0.71023 -0.10497
V6 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V7 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V8 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
round(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V2 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V3 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V4 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V5 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V6 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V7 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V8 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
# estrazione dei dati relativi ai maschi
subset(dati,dati$V5==1)
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
...
67 74 76 0 0 1 170 56 2
68 68 66 0 0 1 172 70 2
# la nuova matrice di correlazione, da cui si vede che, per es.,
# la correlazione tra altezza (V6) e peso (V7) passa da 0.78 a
# 0.59
cor(subset(dati,dati$V5==1))
V1 V2 V3 V4 V5 V6
V1 1.00000000 0.60734884 -0.01479404 0.0580805261 NA 0.0449853579
V2 0.60734884 1.00000000 0.48164645 -0.0157001769 NA 0.0559294175
V3 -0.01479404 0.48164645 1.00000000 -0.0313496568 NA 0.1609605822
V4 0.05808053 -0.01570018 -0.03134966 1.0000000000 NA 0.0003936642
V5 NA NA NA NA 1 NA
V6 0.04498536 0.05592942 0.16096058 0.0003936642 NA 1.0000000000
V7 -0.09475028 -0.06564303 0.18162068 0.1750103679 NA 0.5904647568
V8 0.04484415 -0.11115295 0.01163105 -0.1804916067 NA 0.0525792792
V7 V8
V1 -0.09475028 0.04484415
V2 -0.06564303 -0.11115295
V3 0.18162068 0.01163105
V4 0.17501037 -0.18049161
V5 NA NA
V6 0.59046476 0.05257928
V7 1.00000000 -0.13112832
V8 -0.13112832 1.00000000
Warning message:
In cor(subset(dati, dati$V5 == 1)) : the standard deviation is zero
# la spiegazione "grafica" del fenomeno (i punti relativi all'intero
# campione e quelli relativi ai maschi)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="")
points(dati$V6,dati$V7,col="blue")
points(subset(dati$V6,dati$V5==1),subset(dati$V7,dati$V5==1),col="red")
# Come estrarre/togliere righe o colonne da una tabella
# Vedi qui per un esempio.
# Come unire tabelle. Vedi qui per un esempio.
#
# i coefficienti di correlazione tra le diverse variabili
# [ vedi qui per come associare ad essi un intervallo di indeterminazione ]
cor(dati)
V1 V2 V3 V4
V1 1.00000000 0.61619572 0.052277524 0.12870465
V2 0.61619572 1.00000000 0.576816142 0.04585426
V3 0.05227752 0.57681614 1.000000000 0.06558148
V4 0.12870465 0.04585426 0.065581483 1.00000000
V5 0.28539261 0.30947898 -0.106766917 -0.12904743
V6 -0.21102575 -0.15326188 0.223595030 0.04278398
V7 -0.20322133 -0.16637381 0.224024008 0.20061688
V8 -0.06256772 -0.14110121 0.007323575 -0.12020183
V5 V6 V7 V8
V1 0.2853926 -0.21102575 -0.203221327 -0.062567716
V2 0.3094790 -0.15326188 -0.166373807 -0.141101211
V3 -0.1067669 0.22359503 0.224024008 0.007323575
V4 -0.1290474 0.04278398 0.200616884 -0.120201834
V5 1.0000000 -0.70902885 -0.710227077 -0.104971238
V6 -0.7090288 1.00000000 0.782633130 0.089299812
V7 -0.7102271 0.78263313 1.000000000 -0.004037995
V8 -0.1049712 0.08929981 -0.004037995 1.000000000
# Per avere meno (o più) cifre possiamo usare print e round
print(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.0000 0.6162 0.05228 0.1287 0.285 -0.2110 -0.20322 -0.06257
V2 0.6162 1.0000 0.57682 0.0459 0.309 -0.1533 -0.16637 -0.14110
V3 0.0523 0.5768 1.00000 0.0656 -0.107 0.2236 0.22402 0.00732
V4 0.1287 0.0459 0.06558 1.0000 -0.129 0.0428 0.20062 -0.12020
V5 0.2854 0.3095 -0.10677 -0.1290 1.000 -0.7090 -0.71023 -0.10497
V6 -0.2110 -0.1533 0.22360 0.0428 -0.709 1.0000 0.78263 0.08930
V7 -0.2032 -0.1664 0.22402 0.2006 -0.710 0.7826 1.00000 -0.00404
V8 -0.0626 -0.1411 0.00732 -0.1202 -0.105 0.0893 -0.00404 1.00000
round(cor(dati),3)
V1 V2 V3 V4 V5 V6 V7 V8
V1 1.000 0.616 0.052 0.129 0.285 -0.211 -0.203 -0.063
V2 0.616 1.000 0.577 0.046 0.309 -0.153 -0.166 -0.141
V3 0.052 0.577 1.000 0.066 -0.107 0.224 0.224 0.007
V4 0.129 0.046 0.066 1.000 -0.129 0.043 0.201 -0.120
V5 0.285 0.309 -0.107 -0.129 1.000 -0.709 -0.710 -0.105
V6 -0.211 -0.153 0.224 0.043 -0.709 1.000 0.783 0.089
V7 -0.203 -0.166 0.224 0.201 -0.710 0.783 1.000 -0.004
V8 -0.063 -0.141 0.007 -0.120 -0.105 0.089 -0.004 1.000
# estrazione dei dati relativi ai maschi
subset(dati,dati$V5==1)
V1 V2 V3 V4 V5 V6 V7 V8
1 64 88 1 0 1 168 64 2
2 58 70 1 0 1 183 66 2
3 62 76 1 1 1 186 73 3
...
67 74 76 0 0 1 170 56 2
68 68 66 0 0 1 172 70 2
# la nuova matrice di correlazione, da cui si vede che, per es.,
# la correlazione tra altezza (V6) e peso (V7) passa da 0.78 a
# 0.59
cor(subset(dati,dati$V5==1))
V1 V2 V3 V4 V5 V6
V1 1.00000000 0.60734884 -0.01479404 0.0580805261 NA 0.0449853579
V2 0.60734884 1.00000000 0.48164645 -0.0157001769 NA 0.0559294175
V3 -0.01479404 0.48164645 1.00000000 -0.0313496568 NA 0.1609605822
V4 0.05808053 -0.01570018 -0.03134966 1.0000000000 NA 0.0003936642
V5 NA NA NA NA 1 NA
V6 0.04498536 0.05592942 0.16096058 0.0003936642 NA 1.0000000000
V7 -0.09475028 -0.06564303 0.18162068 0.1750103679 NA 0.5904647568
V8 0.04484415 -0.11115295 0.01163105 -0.1804916067 NA 0.0525792792
V7 V8
V1 -0.09475028 0.04484415
V2 -0.06564303 -0.11115295
V3 0.18162068 0.01163105
V4 0.17501037 -0.18049161
V5 NA NA
V6 0.59046476 0.05257928
V7 1.00000000 -0.13112832
V8 -0.13112832 1.00000000
Warning message:
In cor(subset(dati, dati$V5 == 1)) : the standard deviation is zero
# la spiegazione "grafica" del fenomeno (i punti relativi all'intero
# campione e quelli relativi ai maschi)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="")
points(dati$V6,dati$V7,col="blue")
points(subset(dati$V6,dati$V5==1),subset(dati$V7,dati$V5==1),col="red")
 # la retta di regressione (altezza, peso); lm sta per linear model
x <- dati$V6; y <- dati$V7; plot(x,y)
mod = lm(y ~ x); mod$coefficients; abline(mod)
(Intercept) x
-90.8681981 0.8983596
# y = -90.87 + 0.8984 x (per abline vedi)
# I coeff. potrei memorizzarli con
# b <- mod$coefficients[1]; a <- mod$coefficients[2]
# Nota: confint(lm(y~x),level=…) dà intervalli di confidenza per lm (vedi l'help)
# [ se non trovi ~ nella tastiera, se non hai sottomano questo documento da cui
# copiarlo, … puoi usare help(tilde) e copiarlo dalla pagina che si apre ]
# la retta di regressione (altezza, peso); lm sta per linear model
x <- dati$V6; y <- dati$V7; plot(x,y)
mod = lm(y ~ x); mod$coefficients; abline(mod)
(Intercept) x
-90.8681981 0.8983596
# y = -90.87 + 0.8984 x (per abline vedi)
# I coeff. potrei memorizzarli con
# b <- mod$coefficients[1]; a <- mod$coefficients[2]
# Nota: confint(lm(y~x),level=…) dà intervalli di confidenza per lm (vedi l'help)
# [ se non trovi ~ nella tastiera, se non hai sottomano questo documento da cui
# copiarlo, … puoi usare help(tilde) e copiarlo dalla pagina che si apre ]
 # la figura a destra è stata ottenuta con:
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="");points(x,y)
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod)
# posso cambiare dimensioni/forma/colore dei punti con opzioni
# a points
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod$coefficients); points(x,y, pch=".")
# il primo grafico è stato ottenuto con le righe precedenti, il
# secondo modificando, oltre al colore, le dimensioni dei punti con cex
points(x,y, pch=".", cex=2, col="green")
# il terzo modificamdo la forma dei punti (a pch si dà un numero tra 21 e 25)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="");points(x,y,pch=25)
# la figura a destra è stata ottenuta con:
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="");points(x,y)
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod)
# posso cambiare dimensioni/forma/colore dei punti con opzioni
# a points
plot(c(0,200),c(-100,100),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
abline(mod$coefficients); points(x,y, pch=".")
# il primo grafico è stato ottenuto con le righe precedenti, il
# secondo modificando, oltre al colore, le dimensioni dei punti con cex
points(x,y, pch=".", cex=2, col="green")
# il terzo modificamdo la forma dei punti (a pch si dà un numero tra 21 e 25)
plot(c(150,200),c(40,100),type="n",xlab="", ylab="");points(x,y,pch=25)
 #
# se disponiamo di tre coppie di dati tra due grandezze x ed y che
# sappiamo essere legate da una relazione y = kx e non conosciamo la
# precisione dei dati (altrimenti procederemmo così), possiamo trovare
# la retta di regressione vincolata a passare per (0,0)
x<-c(50,130,230); y <-c(90,240,470)
x1 <- -10; x2 <- 300; y1 <- -20; y2 <- 500
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
points(x,y,col="blue")
k <- mean(x*y)/mean(x^2); k; abline(0,k)
[1] 1.988935
# Ma posso procedere direttamente anche lm(y ~ x - 1) (lm con aggiunto "-1"):
lm(y ~ x-1)$coefficients
x
1.988935
#
# se disponiamo di tre coppie di dati tra due grandezze x ed y che
# sappiamo essere legate da una relazione y = kx e non conosciamo la
# precisione dei dati (altrimenti procederemmo così), possiamo trovare
# la retta di regressione vincolata a passare per (0,0)
x<-c(50,130,230); y <-c(90,240,470)
x1 <- -10; x2 <- 300; y1 <- -20; y2 <- 500
plot(c(x1,x2),c(y1,y2),type="n",xlab="", ylab="")
axis(1,pos=0,label=FALSE,col="brown"); axis(2,pos=0,label=FALSE,col="brown")
points(x,y,col="blue")
k <- mean(x*y)/mean(x^2); k; abline(0,k)
[1] 1.988935
# Ma posso procedere direttamente anche lm(y ~ x - 1) (lm con aggiunto "-1"):
lm(y ~ x-1)$coefficients
x
1.988935
 #
# Ecco come calcolare la covarianza, e come ottenerne la correlazione:
cov(x,y)
# 78.39035
cov(x,y)/sd(x)/sd(y); cor(x,y)
# 0.7826331 0.7826331
#
# Altri esempi reperibili qui:
#
# Ecco come calcolare la covarianza, e come ottenerne la correlazione:
cov(x,y)
# 78.39035
cov(x,y)/sd(x)/sd(y); cor(x,y)
# 0.7826331 0.7826331
#
# Altri esempi reperibili qui:



 #
# il test χ2 (e livelli di confidenza): vedi qui
#
# il test t di Student: vedi qui
#
# Parabola che "meglio" approssima i punti seguenti (vedi qui)
# x <- c(-5,-2.6,-0.4,2.2,3)
# y <- c(-1.3,-2.6,-1,4,5.4)
#
# il test χ2 (e livelli di confidenza): vedi qui
#
# il test t di Student: vedi qui
#
# Parabola che "meglio" approssima i punti seguenti (vedi qui)
# x <- c(-5,-2.6,-0.4,2.2,3)
# y <- c(-1.3,-2.6,-1,4,5.4)
 #
# Altri (tabelle di dati classificati: tabelle di contingenza - vedi) sono
# reperibili qui (prop.table, colSums, rowSums, mosaicplot), qui:
#
# Altri (tabelle di dati classificati: tabelle di contingenza - vedi) sono
# reperibili qui (prop.table, colSums, rowSums, mosaicplot), qui:

 # e qui:
# e qui:
 # la corrispondente gaussiana e la sua ripartizione
z <- function(x) dnorm(x,mean=180,sd=6); plot(z,155,205)
t <- function(x) pnorm(x,mean=180,sd=6); plot(t,155,205)
# la corrispondente gaussiana e la sua ripartizione
z <- function(x) dnorm(x,mean=180,sd=6); plot(z,155,205)
t <- function(x) pnorm(x,mean=180,sd=6); plot(t,155,205)
 # vedi qui per la funzione degli errori erf
#
# gaussiana in forma esplicita
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,m-s,m+s); integrate(f,m-3*s,m+3*s); integrate(f,-Inf,Inf)
0.6826895 with absolute error < 7.6e-15
0.9973002 with absolute error < 9.3e-07
1 with absolute error < 7.6e-06
#
# una distribuzione esponenziale dove rate è 1/m, dexp(x) è rate*exp(-rate*x)
# ("rate" in inglese significa velocità; m infatti esprime il tempo medio nel
# caso in cui la legge rappresenti il tempo tra l'arrivo di due telefonate o
# di due auto ad un semaforo)
curve(dexp(x, rate = 5), col="red", xlab="", ylab = "densitÓ", from = 0, to = 2)
# vedi qui per la funzione degli errori erf
#
# gaussiana in forma esplicita
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,m-s,m+s); integrate(f,m-3*s,m+3*s); integrate(f,-Inf,Inf)
0.6826895 with absolute error < 7.6e-15
0.9973002 with absolute error < 9.3e-07
1 with absolute error < 7.6e-06
#
# una distribuzione esponenziale dove rate è 1/m, dexp(x) è rate*exp(-rate*x)
# ("rate" in inglese significa velocità; m infatti esprime il tempo medio nel
# caso in cui la legge rappresenti il tempo tra l'arrivo di due telefonate o
# di due auto ad un semaforo)
curve(dexp(x, rate = 5), col="red", xlab="", ylab = "densitÓ", from = 0, to = 2)
 # una esponenziale in forma esplicita
h<- function(x) exp(-x*2)*2; integrate(h,0,1);integrate(h,1,Inf);integrate(h,0,Inf)
0.8646647 with absolute error < 9.6e-15
0.1353353 with absolute error < 2.1e-05
1 with absolute error < 5e-07
#
# la distribuzione binomiale di dato ordine e data probabilità
# di successo nella singola prova
plot(0:10,dbinom(0:10,10, 1/2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.8),type="h", lwd=3, xlab="", ylab="")
# una esponenziale in forma esplicita
h<- function(x) exp(-x*2)*2; integrate(h,0,1);integrate(h,1,Inf);integrate(h,0,Inf)
0.8646647 with absolute error < 9.6e-15
0.1353353 with absolute error < 2.1e-05
1 with absolute error < 5e-07
#
# la distribuzione binomiale di dato ordine e data probabilità
# di successo nella singola prova
plot(0:10,dbinom(0:10,10, 1/2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.2),type="h", lwd=3, xlab="", ylab="")
plot(0:10,dbinom(0:10,10, 0.8),type="h", lwd=3, xlab="", ylab="")
 #
# Per studiare, più in generale, le distribuzioni multinomiali, si usa dmultinom: vedi
#
# Una funzione densità bivariata (vedi qui)
#
# Per studiare, più in generale, le distribuzioni multinomiali, si usa dmultinom: vedi
#
# Una funzione densità bivariata (vedi qui)
 # Problema:
# Sappiamo che il 12% della popolazione mondiale e' mancina.
# Qual è la probabilita' che in un campione casuale di 100 persone il
# numero di mancini sia compreso tra 10 e 14 (estremi inclusi)?
sum(dbinom(10:14, 100, 0.12)))
[1] 0.5583493
# alternativa: Pr(10 <= X1+X2+...+X100 <= 14) con Xi = 1/0 a seconda che
# i-ma persona sia o no mancina; ha andamento approssimativamente normale,
# con media 12%*100 = 12 e varianza pari a 100 volte la varianza degli Xi:
# 100*0.12*(1-0.12) = 10.56
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,9.5,14.5)
0.5582977 with absolute error < 6.2e-15
#
# Tre diversi grafici di una poissoniana
k <- 0:20
p <- dpois(k, lambda = 5)
plot(k, p, type = "h", xlab="", ylab="")
plot(k, p, main = "Poisson")
plot(k, p, type = "h", lwd = 6, xlab="", ylab="")
# Problema:
# Sappiamo che il 12% della popolazione mondiale e' mancina.
# Qual è la probabilita' che in un campione casuale di 100 persone il
# numero di mancini sia compreso tra 10 e 14 (estremi inclusi)?
sum(dbinom(10:14, 100, 0.12)))
[1] 0.5583493
# alternativa: Pr(10 <= X1+X2+...+X100 <= 14) con Xi = 1/0 a seconda che
# i-ma persona sia o no mancina; ha andamento approssimativamente normale,
# con media 12%*100 = 12 e varianza pari a 100 volte la varianza degli Xi:
# 100*0.12*(1-0.12) = 10.56
s<- sqrt(10.56); m<- 12; f<- function(x) 1/(sqrt(2*pi)*s)*exp(-(x-m)^2/(2*s^2))
integrate(f,9.5,14.5)
0.5582977 with absolute error < 6.2e-15
#
# Tre diversi grafici di una poissoniana
k <- 0:20
p <- dpois(k, lambda = 5)
plot(k, p, type = "h", xlab="", ylab="")
plot(k, p, main = "Poisson")
plot(k, p, type = "h", lwd = 6, xlab="", ylab="")
 # modi per ottenerne i valori:
p
[1] 6.737947e-03 3.368973e-02 8.422434e-02 1.403739e-01 1.754674e-01
[6] 1.754674e-01 1.462228e-01 1.044449e-01 6.527804e-02 3.626558e-02
[11] 1.813279e-02 8.242177e-03 3.434240e-03 1.320862e-03 4.717363e-04
[16] 1.572454e-04 4.913920e-05 1.445271e-05 4.014640e-06 1.056484e-06
[21] 2.641211e-07
p[5]
[1] 0.1754674
p[2]+p[3]+p[4]
[1] 0.2582880
s<-0; for (i in 2:4) s <- s+p[i]; s
[1] 0.2582880
#
# Per varie distribuzioni aziona:
help(Distributions)
# - è possibile avere sia la legge teorica ("d..." densità,
# "p..." distribuzione) che la generazione sperimentale con runif ("r...").
# Abbiamo visto la binomiale ("...binom"), la poissoniana ("...pois"),
# la normale ("...norm"), la esponenziale ("...exp"). Esempio
plot(0:6,dbinom(0:6,6, 1/8),type="h", lwd=6);
dev.new(); plot(0:6,pbinom(0:6,6, 1/8),type="h", lwd=6)
# modi per ottenerne i valori:
p
[1] 6.737947e-03 3.368973e-02 8.422434e-02 1.403739e-01 1.754674e-01
[6] 1.754674e-01 1.462228e-01 1.044449e-01 6.527804e-02 3.626558e-02
[11] 1.813279e-02 8.242177e-03 3.434240e-03 1.320862e-03 4.717363e-04
[16] 1.572454e-04 4.913920e-05 1.445271e-05 4.014640e-06 1.056484e-06
[21] 2.641211e-07
p[5]
[1] 0.1754674
p[2]+p[3]+p[4]
[1] 0.2582880
s<-0; for (i in 2:4) s <- s+p[i]; s
[1] 0.2582880
#
# Per varie distribuzioni aziona:
help(Distributions)
# - è possibile avere sia la legge teorica ("d..." densità,
# "p..." distribuzione) che la generazione sperimentale con runif ("r...").
# Abbiamo visto la binomiale ("...binom"), la poissoniana ("...pois"),
# la normale ("...norm"), la esponenziale ("...exp"). Esempio
plot(0:6,dbinom(0:6,6, 1/8),type="h", lwd=6);
dev.new(); plot(0:6,pbinom(0:6,6, 1/8),type="h", lwd=6)
 # rbinom simula il fenomeno; ecco come ottenere 20 uscite sperimentali
rbinom(20,6, 1/8)
[1] 1 0 0 3 0 0 0 1 0 1 0 1 2 0 1 0 0 1 0 1
# per ottenere l'istogramma devo, ora, classificare le uscite in
# opportuni intervalli
hist(rbinom(50,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
hist(rbinom(5000,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
# rbinom simula il fenomeno; ecco come ottenere 20 uscite sperimentali
rbinom(20,6, 1/8)
[1] 1 0 0 3 0 0 0 1 0 1 0 1 2 0 1 0 0 1 0 1
# per ottenere l'istogramma devo, ora, classificare le uscite in
# opportuni intervalli
hist(rbinom(50,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
hist(rbinom(5000,6, 1/8),seq(-1/2,6.5,1),right=TRUE,probability=TRUE)
 # Vedi qui per accedere a librerie esterne, ad esempio per caricare
# particolari distribuzioni
#
# Ecco come raggruppare più grafici:
# mar: vettore c(bottom, left, top, right); da' il numero di linee di
# margine per i quattro lati (l'assenza equivale a c(5, 4, 4, 2) + 0.1)
# mfrow: vettore c(m, n); le figure sono tracciate in una tabella di
# m×n: m righe (row) e n colonne (mf sta per "formato dei margini")
vendite <- c(0.12, 0.3, 0.26, 0.16, 0.04, 0.12)
names(vendite) <- LETTERS[1:length(vendite)]
vendite
A B C D E F
0.12 0.30 0.26 0.16 0.04 0.12
par(mfrow=c(2,2), mar=c(3,3,2,1))
barplot(vendite)
pie(vendite)
pie(vendite, col = c("red","purple","blue","green","yellow","orange"))
dotchart(vendite)
# Vedi qui per accedere a librerie esterne, ad esempio per caricare
# particolari distribuzioni
#
# Ecco come raggruppare più grafici:
# mar: vettore c(bottom, left, top, right); da' il numero di linee di
# margine per i quattro lati (l'assenza equivale a c(5, 4, 4, 2) + 0.1)
# mfrow: vettore c(m, n); le figure sono tracciate in una tabella di
# m×n: m righe (row) e n colonne (mf sta per "formato dei margini")
vendite <- c(0.12, 0.3, 0.26, 0.16, 0.04, 0.12)
names(vendite) <- LETTERS[1:length(vendite)]
vendite
A B C D E F
0.12 0.30 0.26 0.16 0.04 0.12
par(mfrow=c(2,2), mar=c(3,3,2,1))
barplot(vendite)
pie(vendite)
pie(vendite, col = c("red","purple","blue","green","yellow","orange"))
dotchart(vendite)
 # ritorniamo alla modalità standard:
par(mfrow=c(1,1))
barplot(vendite)
# ritorniamo alla modalità standard:
par(mfrow=c(1,1))
barplot(vendite)
 #
# Coi comandi precedenti si possono anche affiancare grafici e testo
# in un'unica finestra:
par(mfrow=c(1,2), mar=c(3,2,2,1))
# parte sinistra
f <- function(x) x^2
plot(f,-2,2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# parte destra
plot(c(0,100),c(0,100),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
# una griglia per posizionare il testo (poi posso cancellare la riga)
abline(v=axTicks(1), h=axTicks(2), col="yellow",lty=3)
text(20,100,"Ecco la prova",family="mono",adj=0,cex=2,font=2)
text(-3,90,"di un grafico e un testo",family="mono",adj=0,cex=1.3,font=2)
text(0,80,"ottenuti con R",family="mono",adj=0,cex=1.7,font=2,col="blue")
text(0,25,"Vedi com'Ŕ stata gestita la pag.",family="mono",adj=0,cex=1,font=4)
text(50,10,"Ciao",cex=3,col="red")
#
# Coi comandi precedenti si possono anche affiancare grafici e testo
# in un'unica finestra:
par(mfrow=c(1,2), mar=c(3,2,2,1))
# parte sinistra
f <- function(x) x^2
plot(f,-2,2)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
# parte destra
plot(c(0,100),c(0,100),type="n",xlab="", ylab="",fg="white",xaxt="n",yaxt="n")
# una griglia per posizionare il testo (poi posso cancellare la riga)
abline(v=axTicks(1), h=axTicks(2), col="yellow",lty=3)
text(20,100,"Ecco la prova",family="mono",adj=0,cex=2,font=2)
text(-3,90,"di un grafico e un testo",family="mono",adj=0,cex=1.3,font=2)
text(0,80,"ottenuti con R",family="mono",adj=0,cex=1.7,font=2,col="blue")
text(0,25,"Vedi com'Ŕ stata gestita la pag.",family="mono",adj=0,cex=1,font=4)
text(50,10,"Ciao",cex=3,col="red")
 # Si possono visualizzare testi senza introdurli riga per riga: vedi
# Si possono visualizzare testi senza introdurli riga per riga: vedi
 #
#
#
#