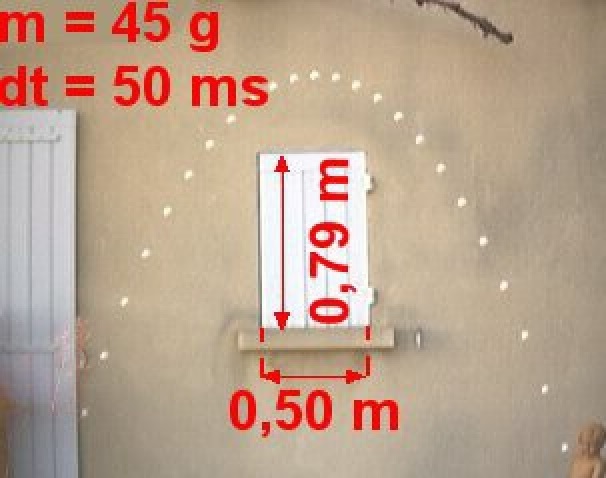
Esempio riferito agli approfondimenti ("La palla da golf") del capitolo 09 qui. Ecco l'immagine riferita ad una palla da golf di 45 g lanciata verso l'alto fotografata ogni 50 ms. Cerchiamo di ricavare un'approssimazione dell'accelerazione.

Carico l'immagine seguente nel seguente modo:
Clicco su questo documento col pulsante destro l'immagine e aziono Copia.
Se voglio posso copiare solo la parte che mi interessa: basta che carichi l'immagine in un'applicazione grafica, ad esempio Paint, selezioni quello che mi serve e lo memorizzi:

aa

Da Cinderella:
Aziono Media browser dal menu File
clicco il bottone "+"
Aziono Paste from clipboard
Clicco Background
Chiudo la finestra con cui ho caricato l'immagine
Ingrandisco la pagina di Cinderella.
Se voglio posso utilizzare al meglio Cinderella riempendo la pagina con l'immagine: posso (vedi) scalare l'immagine usando Mostra Informazione - - "Bachground Image" - "Maximal Aspect" (o "mantenendo le proporzioni").
Con il bottone Aggiungo un punto clicco in corrisponenza dei punti del grafico e, quindi, degli estremi della scala.

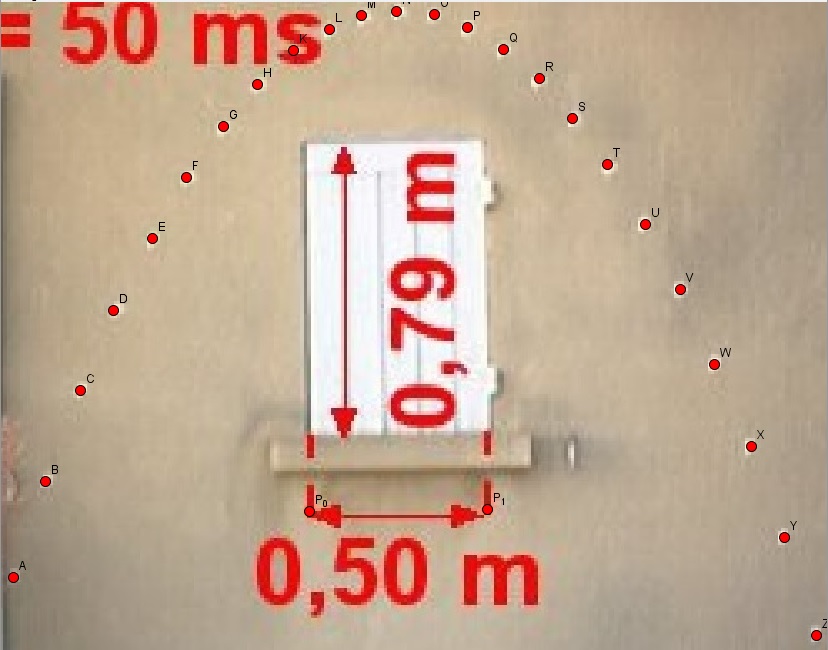
A questo per leggere e, poi, incollare in R (o in altro software) le coordinate mi conviene procedere salvando il testo della costruzione (vedi) ad esempio in un documento PDF e copiare le coordinate, che poi posso facilmente mettere in due variabili ed elaborare e rappresentare graficamente:

source("http://macosa.dima.unige.it/r.R")
x <- c(-8.56,-7.28,-5.88,-4.56,-3,-1.64,-0.16,1.2,2.64,4.08,5.36,6.76,8.28,9.6,11.04,12.48,13.8,15.2,16.72,18.12,19.48,20.96,22.28,23.56)
y <- c(-13.68,-9.84,-6.2,-3,-0.12,2.32,4.36,6.04,7.4,8.24,8.8,8.96,8.84,8.32,7.44,6.28,4.68,2.84,0.44,-2.16,-5.16,-8.44,-12.08,-16)
d <- 10.4-3.28   # Gli estremi del tratto lungo 0.50 metri
scala <- 0.50/d
x1 <- x*scala; y1 <- y*scala
min(x1);max(x1); min(y1);max(y1)
# -0.6011236   1.654494  -1.123596  0.6292135
box(-0.7,1.7, -1.2,0.7); puntini(x1,y1,"red")
# cerco la parabola che approssima al meglio i punti e la traccio
regressione2(x1,y1)
# -1.3 * x^2 + 1.29 * x + 0.316
f <- function(x) -1.3 * x^2 + 1.29 * x + 0.316
graf(f,-1,2, "blue")  # Ecco l'immagine inziale sul computer (in metri)
 

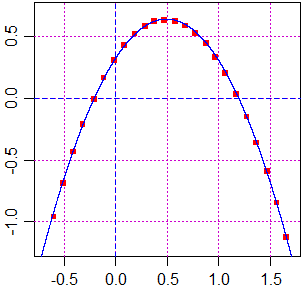
A questo punto esprimo l'altezza al variare del tempo. Tengo conto che le foto sono scattate ogni 50 ms.

length(x1)
# 24
dx <- (max(x1)-min(x1))/23; dx
# 0.09807035
dt = 0.05; t <- x1/dx*dt
regressione2(t,y1)
# -5.02 * t^2 + 2.53 * t + 0.316
# La relazione tra y e t è circa -5*t^2 + .... L'accelerazione di gravità è circa 10 m/s^2.

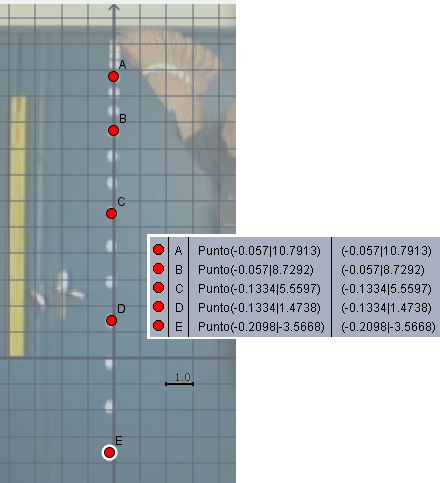
Vediamo un altro esempio sempre riferito agli approfondimenti ("La palla da golf") del capitolo 09 qui. Qui la palla da golf viene lasciata semplicemente cadere (quindi con velocità iniziale nulla); l'intervallo tra uno scatto e l'altro è di 33.3 ms, ossia 1/3 di 1/10 di secondo; l'asta gialla è lunga un metro. • Posso procedere in vari modi. Indicato con y la distanza dal punto A e con x il tempo, posso prendere 3 punti, A, B e D, e cercare la curva y = a*x^2 + b*x + c che passa per essi e poi prendere a = g/2, ovvero g = 2*a: • mi interessa solo la accelerazione, quindi prendo come y di A 0, e, poi, come y di B e D, 0.2 e 0.4 (i punti corrispondono a intervalli di tempo distanziati di 1/10 di secondo); • i valori di y corrispondenti sono (vedi figura a lato, in cui il metro è lungo 10), 1.079, 0.556, -0.357; • risolvo il sistema  c = 1.079 & a*0.04+b*0.2+c=0.556 & a*0.16+b*0.4+c=-0.357; trovo a = -4.875, da cui g = -9.75 (m/s²). Arrotondando g = -9.8 m/s². • Oppure posso procedere come sopra, trovare il polinomio di 2º grado che "meglio" approssima i dati: y <- c(1.079,0.873,0.556,0.147,-0.357); x <- c(0,0.1,0.2,0.3,0.4) regressione2(x,y) #- 4.91 * x^2 + -1.63 * x + 1.08 -4.91*2 # -9.82 Arrotondando, g = -9.8 (m/s²)