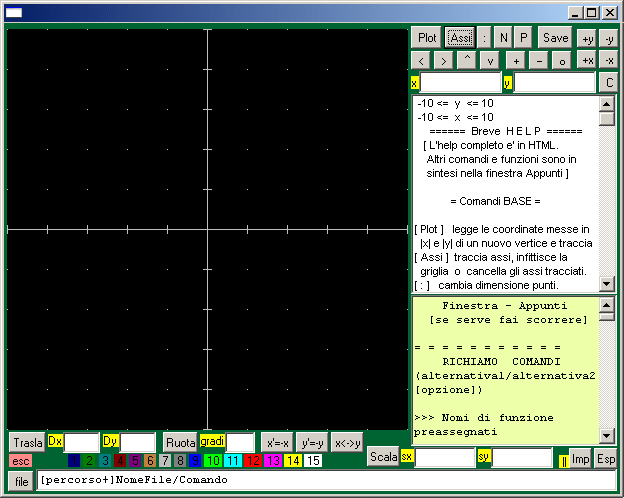
Sotto è illustrata la configurazione a finestra grafica larga (3×2) a cui si può accedere dal link presente sotto al titolo del presente Help.
es. altri programmi RUN
PROGRAMMA per il DISEGNO di POLIGONALI e grafici
ed elaborazioni matematiche VARIE [settembre 2007]
[NOVITÀ rispetto a versioni precedenti:
[La finestra grafica è quadrata (1/1); per una finestra grafica larga (3/2) usa: RUN]
[Se vuoi STAMPARE solo l'help, seleziona fino ad ESEMPI esclusi e scegli l'opzione "stampa selezione"]
Registrazione delle sessioni di lavoro. Il programma, in modo da essere eseguito facilmente via Internet, non occupare grandi spazi di memoria e rimanere di piccole dimensioni, non registra automaticamente le sessioni di lavoro. Se vuoi tenere copia delle elaborazioni che ti interessano registrandole in un unico documento, puoi, ad esempio, aprire un documento di WordPad e incollarvi uscite o comandi (copiati dalla finestra Appunti con Ctrl+C) o immagini (con Alt+Print o Alt+Stamp puoi fare una copia della finestra di Poligon e poi incollarla nel documento di WordPad). Alla fine, se vuoi, alle immagini che hai incollato puoi invertire il colore, tagliare parti inutili, aggiungere commenti, ... selzionandole, incollandole e manipolandole in Paint ed eventualmente riincollandole nello stesso documento, o salvandole come file autonomi (meglio se in formato GIF).
[Plot]: legge le coordinate
messe in X e Y di un nuovo
vertice e traccia.
[Assi]: traccia assi per (0,0),
infittisce griglia o cancella assi
tracciati via via che clicchi.
[ : ] : ingrandisce i punti ad
ogni click.
[N]: inizia una nuova figura e
memorizza temporaneamente
quella attuale; con un doppio
click pulisce anche la finestra
scorrevole.
[P]: richiama la figura di prima,
che puo' essere completata.
Con un doppio click la unisce
alla attuale.
[C]: cancella l'ultimo punto (può essere azionato più volte).
È possibile aprire più volte il programma, tenendone aperte diverse sessioni.
 | ||
 |
Sopra è illustrata la configurazione a finestre ridotte, a sinistra, rimpicciolita, quella a finestre estese, che consente una migliore gestione della finestra appunti. Sotto è illustrata la configurazione a finestra grafica larga (3×2) a cui si può accedere dal link presente sotto al titolo del presente Help. | |
| Nella finestra appunti e nei vari box puoi operare con Copia, Incolla e Taglia azionando questi comandi da tastiera (con Ctrl+C, Ctrl+V e Ctrl+X), dopo aver selezionato o esserti posizionato nei modi usuali (con mouse, tasti direzionali o tasto Tab). |  |
Se vuoi cambiare gli ASSI, scrivi: origine = ... , ... nel box 'file' indicando le coordinate del nuovo punto di incontro degli assi e clicca [Imp]. Puoi anche, contemporaneamente, cambiare il colore degli assi aggiungendo al comando "| CodiceColore" (il colore standard degi assi è "7"; quello della punteggiatura è "8"); con colore negativo gli assi divengono "trasparenti".
Se vuoi far / non far più scrivere la scala anche sui grafici, metti: legenda=1/ =0 nel box 'file' e clicca [Imp].
Se vuoi far apparire una SCRITTA a partire dal punto x,y metti:
scrivi x, y : scritta nel box 'file' e clicca [Imp], o premi Enter;
nella scritta puoi inserire
[ad es.
Se vuoi cambiare dimensione di legenda e scritte puoi usare (nel box 'file', cliccando poi [Imp] o premendo Enter) Font+, Font-, Fontc1, Fontc2, Fontc3, Fontc4, Font= per ingrandire/ridurre le dimensioni o per usare il font Courier di dimensioni diverse (c1 piccolo, ..., c4 molto grande), o per tornare al font standard.
Con Comandi+, Comandi- e Comandi= puoi invece ingrandire/ridurre o riportare alle dimensioni standard i
caratteri del box "file" e della finestra-appunti (con Comandi++ si ottengono caratteri ancora più grandi, e anche sulla
finestra di lista).
Se vuoi cambiare il COLORE di default del tracciamento metti:
color CodiceColore
nel box 'file' e clicca [Imp] o premi Enter;
puoi aggiungere ';' e altri comandi [ad es.
Per RIEMPIRE di un colore una zona, puoi dare il comando
Se vuoi temporaneamente disattivare l'aggiornamento della finestra grafica puoi usare il comando NoPlot=1; con NoPlot=0 puoi riattivare il tracciamento (la cosa può essere utile ad esempio se stai effettuando una serie trasformazioni e non vuoi visualizzare gli esiti di quelle intermedie). Comandi analoghi (NoScrivi=1/0, NoLista=1/0, NoImp=1/0) consentono di disattivare/riattivare le scritte nella finestra-appunti, nella finestra-lista e nei box di Imp (e nei box x e y).
Invece il comando " (virgolette) trasferisce la frase che segue " nella finestra appunti (se la frase è OUT o OUT2 … OUT5 viene trasferito l'ultimo risultato - vedi quanto detto a proposito di "scrivi").
Il comando "" (virgolette+virgolette) memorizza la frase che segue "" ed, eventualmente, la accumula,
preceduta da uno spazio bianco, alla precedente frase che sia stata letta usando lo stesso comando, fino a che non si incontra un comando ", che stampa l'intera frase accumulta e libera la memoria (può essere utile per affiancare uscite). Invece "clip trasferisce quanto accumulato nel Clipboard (la memoria del sistema operativo), che può essere poi trasferito in altri documenti o applicazioni (ad es. si possono costruire - usando anche i comandi indicati nel prossimo paragrafo - liste di dati o di coordinate per i programmi Stat e 3Dim, o per un foglio di calcolo). Questo e i precedenti comandi possono essere utili per i Demo.
Utile è pure il comando stamp=… che se "…" è "#A" ("#B", …,"#Z") accumula alla memoria di cui sopra il termine memorizzato come #A, se "…" è "A CAPO" aggiunge un "a capo", se "…" è "a[](2,3)" aggiunge la matrice 2×3 memorizzata con la variabile indiciata a, se "…" è "IF A=0 A CAPO" (o "IF B=0 … o …) aggiunge un "a capo" nel caso in cui il valore di #A sia 0; altrimenti aggiunge la stringa "…". Invece stamp=#A#B e stamp=#A#B#C accumulano la coppia [terna] dei valori arrotondati dei termini #A e #B [e #C] (separati da virgola e seguiti da "a capo"); l'arrotondamento viene effettuato a 7 cifre o come eventualmente stabilito col comando "cifre" (
[<], [>], [^], [v] : spostano (sinistra,
destra, su, giu') la parte del
piano visualizzata.
[+], [-], [+x], [-x], [+y], [-y] : operano zoom
[o] : sceglie una scala monometrica ottimale
che contenga assi e tutta la
figura; con un doppio click si
adattata meglio alla figura.
Se in Sx metti a..b e in Sy
metti c..d (a,b,c,d numeri)
cliccando su [Scala] (che in questo
caso opera sul sistema di riferimento, non sulla figura: vedi paragrafo seguente) associ alla
finestra il rettangolo cartesiano
[Trasla], [Ruota], [Scala], [x<–>y], [x'=-x],
[y'=-y]: trasformazioni geometriche, secondo gli eventuali
parametri da introdurre nei
riquadri (Sx e Sy sono in questo caso i fattori
di scala). Viene mantenuta la
visualizzazione della vecchia
figura fino a che non si preme
[Assi] o [P] e poi [P] o [>], [<], ...
Altre trasformazioni puoi ottenerle per composizione.
Le
rotazioni sono attorno a (0,0). Per un altro centro di rotazione
mettine le coordinate in Dx e Dy precedute da C (ad es. se in Gradi c'è 30, in Dx c'è c2 e in Dy c'è c-1, viene effettuata una rotazione di 30° attorno a (2,-1).
Se vuoi conservare la figura originale, prima di trasformarla salvala con un nome a tuo piacere; dopo potrai richiamarla.
Oppure clicca [N] e, poi, [P] e, infine, un doppio [P]; a questo punto, quanto la avrai trasformata come preferisci, se azionerai [P] la riavrai sullo schermo al posto del suo trasformato (con un altro [P] riotterrai il trasformato).
Oltre che come sopra, puoi realizzare TRASFORMAZIONI mettendo nel box X e nel box Y, precedute da =, le espressioni di x' e y' in FUNZIONE di x e y, scritte usando il modo di introdurre le funzioni illustrato piu' avanti, e cliccando [Plot]. Ad es.:
con =2*y in X e =2*x+1 in Y
ottieni la figura ribaltata attorno alla retta y=x e traslata verticalmente di 1.
Se in Y aggiungi |CodiceColore, puoi modificare il colore della figura trasformata:
con =2*y in X e =2*x+1 | 14 in Y
ottieni la figura ribaltata attorno alla retta y=x e traslata verticalmente di 1, e colorata in giallo.
Nella descrizione di x' e y', se serve, puoi usare rho e theta come abbreviazioni, rispettivamente,
di SQR(x*x+y*y) e del termine che esprime la direzione (in radianti, come numero tra 0 e 2π) del vettore (x,y).
SALTI, COLORI: introduci 'S'
come X (e premi [Plot]), col riquadro Y lasciato vuoto, per introdurre un salto, ossia
iniziare una nuova spezzata.
Se come y batti 1, 2, ..., 15
la nuova spezzata viene tracciata nel colore di codice 1, 2, ..., 15, secondo la codifica
indicata in fondo alla finestra.
Se fai come sopra con 'C' al
posto di 'S' viene cambiato il
colore di default dell'applicazione, senza introduzione di
salti e memorizzazione di cambi di colore della figura.
TIPO PUNTI: se come x introduci 'T' e come y 1, 2 o 3 (e premi Plot), puoi stabilire la forma dei punti visualizzati quando clicchi [:] : 1: quadrati (sono il tipo d'avvio), 2: triangoli con lato basso orizzontale, 3: triangoli con lato alto orizzontale. In questo modo modifichi il tipo di default. Se vuoi fissare la forma dei punti di una nuova poligonale batti inizialmente in x 'S' (salto) e in y 100, 200 o 300 (per fissare il tipo 1,2 o 3) senza fissare colori, o, ad es., 213 se vuoi il tipo 2 e il colore 13, o 307 se vuoi il tipo 3 e il colore 7. Questa codifica puoi inserirla anche nei file di punti (vedi sotto)."
CONGiungimento: se vuoi disattivare il congiungimento dei punti (di tutti i punti, anche senza aver inserito salti) scrivi: punticong = 0 nel box 'file' e clicca [Imp]. Con punticong = 1 il congiungimento viene riattivato. Nel caso dei grafici di funzione puoi ricorrere ad una opportuna opzione (vedi più avanti) che li fa tracciare (e memorizzare) senza congiungimento.
RETTANGOLI: PLOT con in x a..b e in y c..d traccia il rettangolo con base [a,b] e altezza [c,d]. La cosa è comoda per rappresentare DATI sperimentali e tracciare istogrammi.
[Save]: salva l'immagine in
formato BMP. Al nome aggiungi l'estensione bmp. Se poi
vuoi stamparla ti conviene (da Paint o dall'altra eventuale applicazione con cui l'apri)
invertire i colori. Per risparmiare spazio ti conviene poi risalvarla come GIF.
[Imp], [Esp]: importa/esporta
da/in un file coordinate (e
codici di salti e colori) della
figura. Il nome del file deve
essere scritto nel riquadro in
basso. Nell'esportazione, se esiste gia' il file, al
nome viene aggiunto un N
per prevenire cancellazioni.
[file] apre una finestra di dialogo che ti consente di cercare e inserire automaticamente un percorso+file nel riquadro. [cliccando col pulsante destro su un file nella finestra di dialogo che si apre, puoi aprire il file con BloccoNote e modificarlo]
I file che rappresentano figure (a cui si può dare
qualunque estensione, ma è consigliabile caratterizzarli con
l'estensione gfu) hanno la forma:
- eventuale riga iniziante con ' e seguita dall'indicazione del rettangolo cartesiano iniziale nella forma a..b,c..d
- eventuali righe di commento inizianti con ' (tra cui un eventuale riga di comandi 'COM:…: vedi sotto)
- riga con numero dei punti (o salti o colori)
- righe con le coordinate dei punti (o codici salti e colori) separate da virgola.
Ad es. se sul computer in
C scrivi con BloccoNote:
' per fare un goniometro
8 [8 e' il numero di righe di dati]
s,10
5.5,0
6,0
s,14
6,0
6,.6
s,12
0,.2
salvi il file come Prova.txt,
batti C:\prova.txt nel riquadro,
premi il bottone IMP, batti 5
in Gradi e premi piu' volte
Ruota, ottieni un goniometro.
Nei file puoi indicare le coordinate con i vari modi di rappresentazione dei numeri impiegati nel programma (2/3, r(5), #A, f(0.25), …).
Se usi un simbolo di funzione o di costante (vedi sotto) devi averlo prima definito nel programma (o devi
inserilo nel file con una riga iniziale del tipo
SCALA e COMANDI inclusi nei file: se in testa a un file [vedi sopra] metti ad es.
'-5..7.5,-4.5..4
all'importazione viene presa questa come scala iniziale. Nel caso di una "animazione" (vedi sotto) e' utile mettere questa indicazione nel primo file.
Tra le righe iniziali di commento del file, puoi mettere anche una riga del tipo:
'SCRIVI 3,2: messaggio
che, fa scrivere sullo schermo la frase "messaggio" a partire dal punto di coordinate (3,2)
[o altra frase a partire da altro punto], e una o più righe del tipo:
'COM: comando
in cui puoi mettere un qualunque comando come lo si inserirebbe da tastiera cliccando [Imp] (ad es.
si potrebbe mettere una definizione di funzione che viene poi impiegata per scrivere
le successive coordinate dei punti.
Puoi anche importare una figura dagli Appunti di Windows invece che da file: se copi da un qualunque documento - anche da questo (o scrivi nella finestra-appunti e da lì copi) righe come quelle descritte sopra e poi metti nel box-file CLIP.gfu ("clip" deriva da "clipboard") e azioni IMP (o premi invio) viene automaticamente caricata e tracciata la figura corrispondente; in alternativa clicca il bottone [CLP] tenendo premuto [Ctrl] o [Alt] (per l'uso di [CLP] senza la pressione di tali tasti vedi).
Il modo più comdo per memorizzare figure è salvarle sotto forma di file. Il alternativa il comando
2d[x1, x2] mette nelle variabili indiciate x1, x2
la sequenza delle ascisse e quella delle ordinate della figura attuale (compresi i codici di salto o cambio colore), che poi possono essere
manipolate e rirappresenate gaficamente col comando 2d(....): vedi sotto.
ANIMAZIONI: se il nome del file importato termina con 01.GFU, 02.GFU,.., 99.GFU o 00.GFU al successivo IMP carica auto maticamente quello (iniziante allo stesso modo e) terminante con 02.GFU, 03.GFU,..,00.GFU,01.GFU. Animazioni più sofisticate possono essere eseguite con i file "demo".
FIGURE predefinite: azionando [Imp] con nel riquadro Q [qP] o C [cP] viene tracciato un quadrato o un cerchio [punteggiato]; con PN (1<N<10) si ha un N-agono regolare
(le figure vengono tracciate in scala automatica; con Css il cerchio viene tracciato senza cambiare scala)
Altre figure tracciabili mediante comandi (e [Imp]) sono le seguenti (queste figure, a differenza delle precedenti, vengono aggiunte
sulle schermo, senza cambiare scala):
C(xC, yC, r) cerchio di
centro C e raggio r
C(xC, yC, xP, yP)
cerchio di centro C passante per P
C(xA, yA, xB, yB, xC, yC)
cerchio passante per A, B e C
P(xV, yV, xF, yF)
parabola di vertice V e fuoco F
E(xF1, yF1, xF2, yF2,d)
ellisse di fuochi F1e F2 tale che
d(F1,P) + d(P,F2) = d
I(xC, yC, xV, yV, p) iperbole
di centro C avente V come uno dei due "vertici" e p come pendenza di uno dei due
asintoti.
S(xA, yA, xB, yB) segmento AB.
Se prima di "(" metti |CodiceColore la figura viene tracciata nel colore indicato
Nella finestra Appunti vengono scritte alcune caratteristiche delle figure tracciate.
Per visualizzare le COORDINATE di un punto clicca col mouse su di esso (appaiono nella finestra a destra).
Se clicchi con Shift premuto il punto è anche evidenziato temporaneamente (con un quadretto) sulla finestra-grafici; con premuto Ctrl o Alt il punto assume dimensioni maggiori. Se (entro 10 sec) clicchi un altro punto
viene visualizzata la distanza del nuovo punto dal precedente; se lo fai con Alt premuto viene tracciato (temporaneamente)
anche il segmento che li congiunge e ne viene visualizzata la pendenza e l'inclinazione (tra -90° e 90°).
Per le coordinate dei punti della figura attuale puoi scrivere, ad es., punto(3) nel box di [Imp] e cliccare [Imp]:
ottieni le coordinate del terzo punto
(tra i punti non sono conteggiati le coppie che codificano salti o cambi colore, ma solo i punti effettivi).
Con NumPunti ottieni invece il numero dei punti (se si tratta di una figura chiusa e il punto iniziale coincide
con quello finale, esso viene contato due volte); NumDati include nel conteggio salti e cambi colore.
Con Lung ottieni la lunghezza, con Area ottieni (se si tratta di una figura chiusa) l'area.
Con Centro ne ottieni le coordinate del centroide (o baricentro).
Se si tratta di un insieme di punti disgiunti, puoi ottenerne ascissa e ordinata del centro con MediaX e MediaY.
Invece SommaX, SommaY, MaxX, MaxY, MinX, MinY, SqmX, SqmY
forniscono somma, massimo, minimo e scarto quadratico medio di ascisse e ordinate.
Gli stessi comandi con aggiunta una P forniscono le stesse informazioni (coordinate, numero punti, …) della figura precedente: es.: puntop(3) dà le cordinate del terzo punto della figura precedente; maxp dà la massima ascissa della figura precedente.
Invece, per tracciare temporaneamente un punto di date coordinate x,y si può azionare (con [Imp]) il comando SHOW(x,y) (o SHOW2 per dimensioni maggiori).
SHOW3D(x,y,z) (o SHOW3D2 per dimensioni maggiori) visualizzano temporaneamente il punto (x,y,z) con la prospettiva scelta nell'ultimo comando "3D" (vedi più avanti).
NUMERI. Oltre ai numeri espressi direttamente (come 2 -0.371 3E-7, che sta per 3*10^-7) usando il "punto", non la "virgola", per segnare l'inizio della parte frazionaria, puoi usare Pi per indicare π, Gr per indicare Grado (ossia π/180) e En per indicare il numero e, di Nepero (ma per ex conviene usare EXP), e combinazione di questi usando simboli di operazione e di funzione, predefiniti o precedentemente da te definiti.
3*2^7 sta per 3*(2^7), ossia 3·27
7^(-1)/2*3 sta per (7^-1)/2*3
7^(-1/2)*3 – o 7^-1/2*3 – sta per (7^-(1/2))*3
R3(4)/2 che sta per (3√4)/2
Pi+2^4/R2(3) che sta per π+(2^4)/√3
1+2/3*cos(10gr) che sta per 1+(2/3)*cos(10°)
se ho definito - vedi sotto - G(x)=ABS(x^3) e #K=17, G(-#K) sta per |(-17)^3|
Puoi comunque calcolare valori di termini qualunque e copiarli poi dalla finestra-appunti in cui vengono visualizzati (vedi sotto). Ad es. se clicchi [Imp] con nel suo box:
In ogni caso (anche all'interno di termini e formule) puoi usare %, %1, %2, …, %9 per richiamare il risultato dell'ultimo, del penultimo, del terz'ultimo, … calcolo eseguito.
Il simbolo "%…" compare all'interno del termine che hai definito, per cui ad ogni uso il suo valore, se hai effettuato qualche calcolo, cambia; se vuoi inserire solo il valore, usa "VAL(%…)" invece di "%…".
Ad es. se l'ultimo risultato era stato 3, definisci F(x)=x+% e poi calcoli F(1), F(2), F(3) ottieni: 4, 6, 9; se avessi definito F(x)=x+val(%) avresti ottenuto: 4, 5, 6.
L'uso di "%" è spesso comodo nella effettuazione di calcoli e, nei demo (vedi sotto), può essere utile per non evitare l'impiego di simboli di costante
che potrebbe creare conflitti con altri impieghi degli stessi simboli.
I numeri devono essere compresi strettamente tra -21024 (= -1.79769313486…·10308) e 21024.
FUNZIONI a 1 input. Puoi definire simboli di funzione. Basta che tu metta nel box di [Imp] ad es.:
G(x) = 1+x o:
H(x) = !(x) o:
F(x) = SIN(x^2) o ...
e clicchi [Imp] (o premi Invio), per definire
G(x)=1+x,
H(x)=x!,
G(x)=sin(x2).
Gli altri simboli di funzione sono:
"+", "-", "^", "*", "/","\", "MOD", ">", "<", "=", ">=", "<=" a 2 input;
(a<b, ad es., vale 1 se la relazione è vera, 0 se è falsa)
"–", "SQR", "ABS", "SGN", "COS", "SIN", "TAN", "ASIN", "ACOS", "ATN", "EXP", "LOG", "FIX", "INT", "CINT", "ROUND", "CEIL", "FLOOR" a 1 input (clicca QUI per dettagli); sono stati introdotti anche "LD" e "LB" per i logaritmi decimale e binario; e R2, …, R9 per la radice seconda, …, nona: R3(-27) fornisce 3 mentre (-27)^(1/3) darebbe un errore.
(per indicare x! occorre scrivere !(x); il programma interpreta comunque correttamente 0!, 1!, 2!, …, ossia i casi in cui x è espresso direttamente come numero naturale)
"RND" a 0 input;
Se in un termine si dimentica un simbolo di moltiplicazione "*", in alcuni casi il programma corregge l'espressione automaticamente:
Nel definire una funzione puoi usare funzioni gia' definite. Ad es. se hai def.
F(x) = 1+x^2
G(x) = x-5
puoi ottenere H(x) = (1+x2)/(x-5) e K(x) = 1+(x-5)2 con:
H(x) = f(x)/g(x) e
K(x) = F(G(x)).
Se hai dimenticato come hai definito una funzione F e hai cancellato la finestra-appunti, puoi ottenere la visualizzazione della definizione data battendo
Se invece batti F(x): ottieni la "compilazione" di F(x), ossia la sequenza di assegnazione elementari attraverso cui Poligon esegue il calcolo di F(x). In questo modo è possibile analizzare meglio la struttura dei termini, evidenziare le priorità tra le operazioni, … Ad esempio se hai definito F(x)=x+G(x), G(x)=#A+x*7^x e #a=3, con G(x): e con F(x): ottieni rispettivamente:
v0 = 7 ^ x v0 = 7 ^ x
v1 = x ^ v0 v1 = x ^ v0
v2 = 3 + v1 v2 = 3 + v1
v3 = x + v2
Invece con F(x) (senza ":") ottieni sia la definizione, sia l'espressione che F(x) assume rimpiazzando l'attuale significato dei simboli di funzione che vi appaiono:
x+G(x)
x+(3+x*7^x)
CALCOLI. Se hai definito una funzione F e metti nel box di [Imp] (e poi clicchi Imp o premi Enter):
f(k) con k numero
viene calcolato e scritto nella finestra-appunti F(k)
[a,b] f(x)=k con a,b,k numeri
viene trovato x (e scritto nella finestra-appunti) x in [a,b] tale che F(x)=k, o, meglio, tale che in x il grafico di F scavalchi la retta y=k
[a,b] f max con a,b numeri
viene trovato max di F in [a,b] se ivi F ha andamento /\
[a,b] f min con a,b numeri
viene trovato min di F in [a,b] se ivi F ha andamento \/
[a,b] f Int con a,b numeri
viene trovato l'integrale di F in [a,b]
[a,b] f IntD con a,b numeri
calcola l'integrale di F in [a,b] senza usare interpolazioni (senza approssimare
l'andamento di F con funzioni polinomiali): metodo meno preciso del precedente per le funzioni continue ma più affidabile in presenza di punti di disconinuità.
[a,b] f Sum con a,b numeri interi
viene trovato F(a)+F(a+1)+...+F(b), ossia Σi=a..bF(i).
Altri calcoli:
[a,b] x[] Sum con a,b numeri interi
viene trovato x[a]+x[a+1]+...+x[b] (x[] variabile indiciata: vedi)
[a,b] x[] Med con a,b numeri interi
viene trovata la media di x[a],x[a+1],...,x[b]
[a,b] x,y[] Chi2 con a,b numeri interi
viene trovato χ2 delle frequenze assolute osservate x[a]...x[b]
rispetto alle frequenze attese y[a]...y[b] (in y[], non in x[],
posso essere messe indifferentemente le frequenze assolute o quelle relative o quelle percentuali o valori ad esse proporzionali)
FATT(k) con k numeri intero
k viene scomposto in fattori primi.
FAT1(k)
calcola il 1° divisore primo (>1) di k
SUBV(#x=T1, #y=T2, …, #A)
calcola il valore che assume il termine rappresentato con la costante #A (vedi sotto)
dopo aver sostutito #x, #y, … con i termini T1, T2, …
det(A)(N)
calcola il determinante della matrice N×N A (vedi)
Se vuoi assegnare il risultato di uno di questi calcoli a una costante o a una variabile indiciata usa "%", o val(%) (vedi).
Nel caso dei comandi "[a,b] …" puoi anche assegnare direttamente il valore calcolato a una costante (non a una variabile indiciata); ad esempio puoi usare
Puoi anche calcolare somme, differenze (non negative) e prodotti di numeri naturali di lunghezza qualunque, se li hai assegnati a due costanti #x e #y, coi comandi seguenti. Le espressioni ottenute le puoi riutilizzare usando #% (vedi) o puoi impiegare
direttamente assegnazioni del tipo
#x [+] #y= #x [-] #y= #x [*] #y=
Puoi anche effettuare calcoli diretti: nel box di [Imp] puoi mettere termine = o =termine ("=" seguito o preceduto da un termine privo di variabili). Ottieni la visualizzazione del suo valore. Ad es. con:
(1/12)+(1/8)= ottieni: 0.20833... (ed anche: 5/24)
R2(30)*R2(45)/3= ottieni: 12.2474... (ed anche: 5R2(6))
1/EN= ottieni il valore di '1/e'.
I risultati che compaiono nella Finestra Appunti sono tutti in formato testo, copiabili e incollabili in altri documenti.
Se non ottieni uscite, vuol dire che il procedimento ha comportato dei calcoli di funzione per input al di fuori del dominio o delle situazioni di overflow
(valori maggiori o uguali in valore assoluto a 2^1024).
Altre COSTANTI
Oltre a Pi, Gr ed En puoi usare come simboli di costante #A, #B, ..., #Z. Basta che tu metta nel box di Imp, ad es.
#A = 1/sqr(2)
per memorizzare 1/√2 come #A. Poi puoi usare #A nelle definizioni di funzioni o in calcoli vari.
Nota: puoi assegnare a una costante un termine contenente altri simboli di funzione o di costante, così che una ridefinizione di qualcuno di essi comporta anche una ridefinizione di tale costante (in pratica in Poligon i simboli di costanti rappresentano dei "termini numerici"). Se vuoi assegnare alla costante il valore che attualmente ha il termine t che le vuoi assegnare devi usare "=VAL(t)" invece di "=t". Ad esempio dopo:
#A=3 #B=#A+1 #C=VAL(#A+1) #A=5
#B vale 6 mentre #C vale 4; se poi faccio:
#B=VAL(#B+1) #C=#C+1
#B viene incrementato di 1, mentre se cerco di ottenere il valore di #C ottengo un messaggio di "loop" in quanto si entra in un "circolo vizioso" (se voglio incrementare di 1 #I devo usare #I=VAL(#I+1), non #I=#I+1).
Se azioni #A o #A= ottieni il valore attuale di A. Per ottenere l'espressione di #A devi azionare #A:
Puoi definire più costanti in un'unica riga, separando le assegnazioni con
[Imp] con #C=3; c:\figura.txt
importa il file figura.txt sostituendovi le occorrenze di #C con 3;
[Imp] con #A=2; #B=2/7; [-5,5] f int
calcola l'integrale di F tra -5 e 5 dopo aver sostituito #A con 2 e #B con 2/7.
Nel definire una "costante" puoi usare SUBS e SUBV per ottenerla per sostituzione a partire da un termine già
associato ad un simbolo di costante.
#A =
Ad esempio se ho indicato con #d la distanza del punto (#x,#y) da (0,0):
#D = SQR(#X^2+#Y^2)
posso ottenere che #k sia la distanza dal punto (2,5) con:
#K = SUBS(#x=(2-#x), #y=(5-#y), #d) che (rimpiazzando "#x" con "(2-#x)" e "#y" con "(5-#y)" - ho aggiunto delle parentesi in modo che tutta l'espressione sia elevata al quadrato) fornisce:
#K = SQR((2-#X)^2+(5-#Y)^2)
mentre con:
#K = SUBV(#x=3, #y=7, #d) (rimpiazzando "#x" con "3" e "#y" con "7", e calcolando il valore del termine ottenuto) fornisce:
#K = 7.6157731058639 come se fosse:
#K = VAL(SQR(3^2+7^2))
SUBS e SUBV possono essere usati direttamente, invece che per assegnazioni, per,
rispettivamente, realizzare (temporaneamente) e visualizzare sostituzioni
(che poi possono essere copiate e incollate per costruire altri termini, eventaulemnte in modo automatico: vedi "nota" seguente) o per effettuare calcoli (vedi sopra). Ad es.
SUBS(#X=(2-#X),#Y=(5-#Y),#D)
SUBV(#X=3,#Y=7,#D))
producono:
SQR((2-#X)^2+(5-#Y)^2)
7.615773105863909 = R2(58)
Nota. Ad ogni realizzazione di una sostituzione usando SUBS nel secondo modo ora descritto
(ossia non in assegnazioni ma solo per visualizzare sostituzioni), o di un comando …[+]…= o …[-]…= di somma/differenza tra numeri naturali,
il termine ottenuto viene memorizzato e può essere utilizzato successivamente nella costruzione
di nuovi termini usando #% (o #%0) al suo posto.
Analogamente #%1, #%2 e #%3 consentono di richiamare il penultimo, il terzultimo e il quartultimo termine ottenuto per sostituzione.
Si osservi che SUBS(#T) senza sostituzioni esplicitate mette in #% l'espressione di #T.
Ad esempio per definire il termine T = A + H(2,B) + H(1+Y,7) dove H(x,y)=|√(x+y)| posso fare:
#H = ABS(SQR(#X+#Y)
SUBS(#X=2, #x=#B, #H)
SUBS(#Y=7, #x=1+#Y, #H) (non SUBS(#x=1+#Y, #Y=7, #H) altrimenti perderei #y)
#T = #A + #%1 + #% ottenendo:
#T = #A + ABS(SQR(2+#B) + ABS(SQR(1+#Y+7)
Abbreviazioni. Nel battere le espressioni che impieghi per definire funzioni, costanti o variabili indicate puoi usare le abbreviazioni #rho, #theta e #cbin che vengono automaticamente rimpiazzate dalle stringhe che rappresentano i termini che esprimono il modulo e la direzione (in radianti, come numero tra 0 e 2π) del vettore (#x,#y), e il coefficiente binomiale C(#n,#k). Se vuoi poi puoi rimpiazzare #x, #y, #n e #k con SUBV.
Variabili indiciate.
Puoi usare anche le variabili a 1 indice x[],y[],z[],u[],v[],w[] con indice da 0 a 400 (ad es. x[3], u[150] o z[#j] se a #j è stato assegnato un valore
non negativo e non superiore a 400),
e le variabili a 2 indici a[],b[],c[],d[],e[],f[] e i[] con indici da 0 a 10 (ad es. a[2,7] o e[#i,#j+1]); i[] non è modificabile e vale 1 se gli indici sono uguali, 0 altrimenti (corrisponde alla matrice identità).
Per semplicità, non sono previsti comandi di "dimensionamento"; le dimensioni sono da indicare (come illustrato sotto) in eventuali comandi di stampa, di calcolo, …
Per assegnare un valore a una variabile indiciata, ad es. il valore 2+#a a x[2], scrivi x[2]=2+#a nel box di Imp (e premi Invio).
Nota: in x[2] viene memorizzato il valore di 2+#a, non il termine 2+#a (se riassegni il valore ad #a x[2]
non viene modificato, a differenza di quanto accade con i simboli di costante considerati sopra).
Alle variabili a 1 indice puoi assegnare valori anche come nei seguenti esempi (al posto di x, y, … puoi mettere una qualunque
altra variabile indiciata):
• x[] = 1,2,3,4,5,6,7,8,9,10,11,12
questo comando equivale a: x[0]=1; x[1]=2; ...; x[11]=12
• x[] = x[]+y[]
questo comando equivale a: x[0]=x[0]+y[0]; ...; x[400]=x[400]+y[400]; analoghi comandi con "*", "-", "/", "^"
(le stesse cose si potrebbero fare con un ciclo FOR, ma così la cosa è più comoda);
• x[] = x[]+T (T termine; analoghi comandi con "*", "-", "/", "^", "=", ">", "<") addiziona T x[0], x[1], ...
• x[] = [T] equivale a x[0]=T, x[1]=T, ..
• x[] = i equivale a x[] = 0,1,2,3,…,400
• x[] = f(y[]) equivale a x[] = f(y[0]),f(y[1]),…,f(y[400])
Per visualizzare i primi 8 valori x[0],...x[7] puoi usare:
• x[](7) = (o x[](7)/ = per la stampa in colonna)
• x,y[](7) = o xcy[](7)/ = per la stampa in colonna
affiancati e separati da "," (o da un qualunque carattere c) degli elementi di indice 0, 1,...,7 di x[] e y[].
Alle variabili a 2 indici puoi assegnare valori anche come nei seguenti esempi:
• a[](2,3) = 1,2,3,4,5,6 (matrice 2×3)
questo comando equivale a: a[1,1]=1; a[1,2]=2; a[1,3]=3; a[2,1]=4; a[2,2]=5; a[2,3]=6 (gli indici vengono considerati a partire da 1 per interpretarli come "righe" e "colonne")
• a[](5,4) = b+c a[](5,4) = b-c
per definire una matrice (5×4) come somma o differenza di altre;
• a[](2,7) = b a[](2,7) = #k*b
per assegnare a una matrice (2×7) i valori di un'altra matrice b, o i valori di b moltiplicati per una costante #k (le costanti devono essere della forma #a,...,#z);
• a[](3,2) = b*c(5)
per assegnare a una matrice (3×2) il prodotto di b (3×5) per c (5×2);
• a[](4,4)=inv(b) a[](4,4)=tri(b) a[](2,7)=trasp(b)
per assegnare a una matrice (4×4) la matrice inversa o la matrice triangolarizzata della matrice b (4×4) o a una matrice (2×7) la trasposta di una matrice b (7×2);
• a[](4,6) = RND
per assegnare a caso a una matrice (4×6) valori interi tra -9 e 9 (comodo per studio sperimentale / congetture su proprietà delle matrici, o per demo con esercizi);
Atri comando per le variabili a 2 indici sono:
• det(a)(3) =
per calcolare il determinante della matrice 3×3 costituita da a[1,1],...,a[3,3]
• a[](5,6) =
per stampare la matrice 5×6 costituita da a[1,1],...,a[5,6]
Puoi importare grafici vari (come file nel formato sopra descritto) realizzati con GraFun.bas
o con lo script graf.htm presenti negli Oggetti Matematici (in cui puoi introdurre mediante sottoprogrammi funzioni di qualunque complessità), o con altri programmi.
Ma puoi realizzare GRAFICI anche direttamente:
# definisci una funzione F (vedi sopra)
# metti -3..5 N=50 nel box X e F nel box Y se vuoi approssimarne il grafico in [-3, 5] con una poligonale di 50 lati (o 2..10 N=300 o ...). Se metti solo -3..5 viene automaticamente preso N=101.
# in Y metti F|14, F|5,... (aggiungi | e codice colore) se vuoi un grafico giallo, viola, ...
# in X metti N=50P o N=300P (aggiungi P) se vuoi che siano tracciati solo i punti (i vertici della poligonale): utile per funzioni non continue o non definite su intervalli (se ti è utile, tiene presente che la finestra grafica è di 400 per 400 pixel).
# clicca [N] solo se vuoi pulire la finestra
# clicca [Plot]
# fai un eventuale [doppio] clic su [o] (il grafico potrebbe non essere nella parte di piano cartesiano attualmente visualizzata)
# prima di azionare [Plot] puoi mettere nel box SY un intervallo a..b per evitare il tracciamento di eventuali asintoti verticali (punti troppo fuori da esso vengono saltati).
Es.: x [ -5..5 n=500 P ] y [ g | 14 ]
Puoi anche tracciare una CURVA in forma parametrica:
# definite due funzioni F e G,
# metti nel box X -3..5 N=50 (o ...) e F,G (ed eventalmente |CodiceColore) in Y
# clicca [Plot] e ottieni P=P(t) con -3 <= t <= 5.
Es.: x [ -5..5 n=500 P ] y [ h,g | 14 ]
Se vuoi descriverla in forma polare, ad es. come ρ=1/(1+0.8*cos(θ)), puoi definire:
R(x) = 1/(1+0.8*cos(x)), F(x) = R(x)*cos(x), G(x) = R(x)*sin(x)
e tracciare, nel modo appena detto, la curva in equazioni parametriche x=F(t), y=G(t)
Puoi infine tracciare una CURVA descritta come F(x,y) = k se hai def. una funzione F a 2 input (vedi sotto):
# metti nel box X f(x,y)=k con k numero [se vuoi aggiungi | CodiceColore ]
# metti nel box Y a..b | c..d e fai [Plot]
# verranno tracciati punti in [a,b]×[c,d] che soddisfano f(x,y)=k
# in X compare N=40. Se vuoi piu' punti rifai [Plot] con N maggiore (cambia 40 ad es. in 80)
# eventualmente clicca [:] per ingrandire i punti
Se posizioni il mouse su [ESC] il tracciamento viene arrestato.
Es.: x [ h(x,y)=3 | 14 ] y [ -5..5 |-3..7 ]
Volendo puoi tracciare curve usando un ciclo FOR (vedi sotto); ad es.:
FOR #I=0 TO 100: #T=pi+(8*pi-pi)/100*#I; PLOT X:30*cos(#t)/#t Y:30*sin(#t)/#t
traccia la curva x=30·cos(t)/t, y=30·sin(t)/t per t in [π,8π].
Infine si possono rappresentare figure le cui coordinate siano memorizzate in variabili indiciate:
2D(x1, x2, N) traccia la poligonale P(0),..,P(N) con coordinate xP(i) e
yP(i) nelle variabili indiciate x1,x2.
2D|Col(..) la traccia col colore di codice Col.
Sono conteggiati tra i P(i) anche i dati che rappresentano salti e cambi di colore.
FUNZIONI a 2 input.
Puoi definire (impiegando la notazione
per scrivere i termini gia' descritta
per le funz. a 1 input) funzioni a 2
input usando x e y come variabili.
Ad es. se premi [Imp] con:
H(x,y) = abs(sqr(x+y))
definisci h(x,y) = |√(x+y)|
Puoi usare le funzioni a 2 input
per tracciare grafici di curve
descritti in forma implicita come
f(x,y)=k.
Puoi anche calcolarne valori.
Ad es. se definisci:
d(x,y) =SQR( (x-3)^2 + (y-4)^2 )
con d(5,7) [Imp] puoi calcolare la
distanza di (5,7) da (3,4).
Non puoi usare simboli di funzioni a 2 input all'interno di altre definizioni o di calcoli di termini. Puoi ovviare a ciò usando SUBS (vedi).
Per i loro grafici vedi più avanti.
Nella definizione di una funzione a 2 input puoi usare rho e theta come ABBREVIAZIONI, rispettivamente,
di SQR(x*x+y*y) e del termine che esprime la direzione (in radianti, come numero tra 0 e 2π) del vettore (x,y).
FUNZIONI PREDEFINITE a 1 input:
Se con [Imp] introduci f(x)= o
a(x)= o g(x)= o ... seguito da:
GAUSS
a F (o A o G o ...) viene associata la funz. di densita' normale di media #M e s.q.m #S;
BINOM
viene associata Pr(U=x) con U variabile casuale binomiale #n,#p;
FUNZIONI PREDEFINITE a 2 input:
Se con [Imp] introduci f(x,y)= o
a(x,y)= o ... seguito da:
MODULO
a F (o A o ...) viene associato il
modulo del vettore (x,y), ossia
DIREZIONE
viene associata la direzione in gradi del vettore (x,y) (equivale a mettere …=THETA/GR)
CBIN
viene associato il coefficiente binomiale C(x,y) (quantita' di sottoinsiemi di y elementi da un insieme di x elementi)
Si possono realizzare anche altri tipi di TRASFORMAZIONI piu' complesse, operanti non punto per punto:
se a destra di '=' si mettono x0 o x1 questi sono interpretati come la x precedente e la x successiva.
Analogamente y0 e y1 sono la y precedente / successiva (la nuova figura avrà 1 o 2 punti in meno). Ad es. con:
=x nel box X e =(y-y0) nel box Y
cliccando [Plot] si ottiene il grafico della variazione della y del grafico precedentemente tracciato.
Alcune trasformazioni sono predefinite. Basta mettere in Y =DERIV per avere automaticamente il grafico della pendenza; mettere =MEDMOB per quello trasformato con le medie mobili (con =MEDMOB1 sono conservati 1° e ultimo punto).
Nel definire le trasf. puoi usare %:
viene inteso come il valore di y precedentemente calcolato. Prima di fare una trasformazione in cui usi % devi tracciare un punto che sia preso come punto inziale.
Ad es. se hai tracciato y=x tra 0 e 10 in 10 passi - ossia i punti (0,0), (1,1),...,(10,10) - e poi tracci (0,1) e operi la trasformazione:
=x in X, =%*x in Y (man mano y viene moltiplicato per il nuovo x) ottieni il grafico del fattoriale - ossia i punti (0,1),...,(n,n!),...,(10,10!)
(se vuoi vederne i valori usa [Imp] con punto(1), punto(2), ...)
Una trasformazione con % e' gia' predefinita: se che metti in Y =INTEGR ottieni automaticamente il grafico della funzione che ha come derivata la F di cui hai appena fatto il grafico ( in un certo [a,b] ) e che passa per il punto (a,...) che hai tracciato prima di azionare INTEGR
(per tracciare il grafico di una "funzione integrale" puoi usare in alternativa un ciclo For che con il comando Plot tracci (#x,#y) con #x del tipo #a+#i*#h e #y del tipo [#a,#x] F Int).
La FINESTRA in basso a destra e' usabile per APPUNTI. Puoi agire su essa (come in tutti i box) con Ctrl+C e Ctrl+V. In essa man mano appaiono anche le funzioni via via definite, risultati di calcoli, …
Nella PRIMA RIGA della finestra a lato della finestra-grafici vengono man mano registrate le attivita' dell'utente e le coordinate dei PUNTI su cui si CLICCA.
Appena hai scritto un comando invece di cliccare [Imp] puoi premere il tasto Enter/ACapo
Invece di premere i vari BOTTONI puoi spostarti su di essi con il tasto di tabulazione (
Per chiudere il programma, invece di cliccare sul pulsante [x] di chiusura della finestra puoi premere Alt+F4.
COMANDI da TASTIERA
Non solo i comandi azionabili con [Imp] - vedi sopra - ma tutti i comandi (tranne quello corrispondente a [Save]) possono essere inseriti da tastiera, senza usare bottoni. Basta posizionarsi nel box "file" scrivere il comando, in uno dei modi sotto descritti, e premere Enter (o cliccare [Imp]):
plot x:… y:… per comandi da azionare con [Plot] mettendo dopo x: e y: quanto si metterebbe nei box "x" e "y";
scala sx:… sy:… per ... [Scala] ... nei box "x" e "y";
trasla dx:… dy:… per ... [Trasla] ... nei box "dx" e "dy";
esp file: Percorso+NomeFile;
o per [o]; oo per [o] con doppio click
n per [N]; nn per [N] con doppio click
p per [P]; pp per [P] con doppio click
assi : < > … x<->y per [Assi] [:] [<] [>] … [x<->y].
canc per [C] (non si è usato C in quanto impiegato per il cerchio predefinito);
error mette in "%" 1 o 0 a seconda che nell'ultimo calcolo via sia stato o no un errore (ad es. di fuori-dominio): è utile nei demo per comandare eventuali salti di parti da non eseguire nel caso ad es. una funzione non fosse definita in un dato punto;
pmeno N (N intero positivo), invece, cancella gli utlimi N punti tracciati; con un successivo p
è possibile riottenere la figura come era prima della cancellazione.
Ad esempio se si è tracciato
un grafico di funzione con 101 lati - quantità di segmentini standard - il comando
I comandi eseguiti compaiono poi sulla finestra appunti ed è possibile ricopiarli (ed eventualmente modificarli) se si devono rieseguire essi o comandi simili (nel box "file" puoi copiare una sola riga
per volta; se vuoi incollare più righe che hai già copiato devi scrivere CLIP nel box: vedi più avanti).
Puoi anche mettere più comandi in un'unica riga separati da "_".
Essi vengono eseguiti uno dopo
l'altro come se fossero stati azionati in successione (un ciclo FOR può essere presente solo nell'ultimo
comando concatenato). Ad es.
l'unica riga:
x[]=4,6,8,5 _ y[]=x[]*x[] _ y[](3)= _ #s=[0,3] y[] sum
definisce due variabili indiciate e stampa y[0],y[1],y[2],y[3] e assegna ad #s la somma y[0]+y[1]+y[2]+y[3]
Se separi due comandi con più "_", ad ogni ulteriore "_" viene effettuata una sosta di un secondo
tra l'esecuzione di un comando e quella dell'altro.
Se hai già scritto una riga di
comandi in qualche documento e l'hai copiata, invece di incollarla nel box File e cliccare [Imp],
puoi più semplicemente cliccare il bottone [CLP].
File DEMO
Puoi costruire file con estensione .DM contenenti riga per riga i comandi da eseguire nel formato "da tastiera"
appena descritto. Richiamando un file DM con [Imp] i comandi in esso elencati vengono eseguiti automaticamente e,
in assenza di altre specificazioni, alla distanza di 1 sec di uno dall'altro.
Se posizioni il mouse su [ESC] l'esecuzione del demo viene arrestata. Se lo posizioni su [File] il demo viene sospeso, ma non cancellato dalla memoria: appena si sposta il mouse da [File] l'esecuzione riprende (ma se si sposta su [Esc] si arresta definitivamente);
conviene avviare il demo cliccando su [Imp] invece che premendo Invio se si vuole che il puntatore del mouse rimanga meglio visibile.
Nei demo puoi usare anche i seguenti comandi:
tempo T (T numero positivo, intero o no) per cambiare, dal punto in cui è inserito fino a un altro comando "tempo", il tempo (in secondi) che intercorre tra un comando e il seguente;
sosta T per introdurre una sosta durante l'esecuzione;
stop per sospendere l'esecuzione fino a che l'utente non agisce nel modo suggerito dal messaggio che appare nel box "file";
axes N (N 0, 1 o 2) per impostare il tipo di assi/griglia (niente, assi, assi con griglia fitta);
punt N (N 0, 1 o 2) per impostare il tipo di punto (punto, quadratino, quadrato);
for #..=.. TO ..: comando per eseguire un ciclo FOR (costituito da un unico comando, eventualmente preceduto da altri comandi del tipo #a=…, #b=… separati da ';': vedi);
come variabile-contatore si usa un simbolo di costante (usato globalmente, non localmente); prima e dopo "TO" vanno messi primo e ultimo valore del contatore; il contatore subisce incrementi unitari;
--- (o ----…) per interrompere l'esecuzione del demo
(ad es. per separare comandi che al momento non si vogliono eseguire);
Nei demo puoi mettere righe di commento (e indicazioni di scala) come nei file contenenti figure. Può essere comodo usare i comandi noplot, noscrivi , nolista (e noimp) per evitare visualizzazioni interemedie non necessarie.
Se vuoi inserire una scritta sul grafico e la scala viene scelta automaticamente, puo' essere utile, per posizionare la scritta, determinare le coordinate cartesiane dei vertici della finestra-grafici:
se usi i comandi xmin, xmax, ymin o ymax ottieni il calcolo e la visualizzazione della coordinata che ti interessa (il suo valore viene messo in "%" come nel caso di tutti i calcoli); questi comandi sono usabili anche al di fuori dei demo.
Se mentre clicchi su [Imp] per avviare un demo tieni premuto il tasto "+" / "–" il demo viene eseguito più / meno velocemente.
Per progettare un demo ti conviene usare Poligon dando i comandi da tastiera, in modo che dalla finestra-appunti tu possa ricostruire o copiare i comandi da inserire nel demo.
Vi sono alcuni comandi inseribili nei Demo che consentono di realizzare algoritmi e veri e propri programmi:
goto N if #… < X (N = 0, 1, … o 9) per saltare alla riga del demo formata dalla parola LABELN nel caso in cui la costante #… (#A, … o #Z) sia minore del numero X;
goto N if …[…] < X (N = 0, 1, … o 9) per saltare alla riga del demo formata dalla parola LABELN nel caso in cui la variabile indiciata …[…] (a[1,1], a[1,2], … o z[400]) sia minore del numero X;
goto N if %M < X (N, M = 0, 1, … o 9) per saltare alla riga del demo formata dalla parola LABELN nel caso in cui l'ultimo, il penultimo, il terz'ultimo, … (a seconda che M sia 0, 1, 2, …) risultato ottenuto sia minore del numero X (al posto di "%0" puoi usare "%");
e comandi analoghi con ">" e "=" al posto di "<".
labelN (N = 0, 1, … o 9) per indicare un punto del demo in cui ri-indirizzare l'esecuzione mediante un GOTO (si possono usare al più 10 "etichette").
Con il seguente comando si può introdurre una sospensione nel caso in cui …:
stop if #…
Per riassegnare "variabili" come #A, #B, … è spesso necessario usare VAL: vedi "definizione costanti".
Esportando/importando file, si possono superare i limiti di memoria legati all'uso delle sole 36 "variabili" #A,..., #Z, %0,..., %9 (i valori importati da file possono essere richiamati calcolando "punto(N)" - o "puntop(N)" - e poi usando %1 e %0).
Prima di azionare un demo, conviene (usando il mouse pulsante destro nella finestra di dialogo che si apre con [file]) aprire il testo del demo e vedere le eventuali righe di commento.
Un ulteriore comando inseribile nei demo è open NomeFile.dm. Con esso si può trasferire (definitivamente) l'esecuzione al demo NomeFile.dm, a patto che esso sia collocato nella stessa cartella in cui si trova il demo "di partenza". Se si aggiungono, sulla stessa riga di un comando "open" un ; e un altro comando (ad es. un goto ...) si può far sì che all'avvio del nuovo demo venga eseguito il comando indicato (se si inserisce un "goto" si può far eseguire il demo a cui ci è trasferiti solo a partire da un certo punto).
Esecuzione diretta di Demo e di Cicli For
Puoi anche importare un demo dagli Appunti di Windows invece che da file: se copi da un
qualunque documento - anche da questo (o scrivi nella finestra-appunti di Poligon e da lì copi)
il testo di un demo, ad es. le righe seguenti, e poi metti nel box-file CLIP.dm (o solo clip) e
azioni IMP (o premi Invio)
vengono automaticamente caricati ed esegiiti i comandi corrispondenti
(in questo caso il tracciamento di un particolare poligono a 11 lati);
in alternativa puoi cliccare il bottone [CLP],
che aziona direttamente l'esecuzione dei comandi memorizzati.
Se i comandi sono molti è, comunque, più comodo costruirsi un file DM.

#n=11
tempo 0.1
n
label0
plot x:5*cos(#n*2*pi/11) y:5*sin(#n*2*pi/11)
#n=val(#n-1)
goto 0 if #n > -1
Una versione alternativa:
noscrivi=1
for #n=0 to 11: plot x:5*cos(#n*2*pi/11) y:5*sin(#n*2*pi/11)
noscrivi=0
Se vuoi eseguire solamente un ciclo (o un doppio-ciclo) FOR (vedi), puoi batterlo direttamente nel box-file e premere invio.
La cosa equivale a mettere in memoria tale riga (preceduta da NoScrivi=1 e NoLista=1 e seguita da NoLista=0 e NoScrivi=0) e all'azionamento di CLIP.
Ad esempio il poligono ottenuto coi demo precedenti puoi ottenerlo battendo direttamente (o cliccando [CLP] dopo aver selezionato e copiato in memoria) solo:
for #n=0 to 11: plot x:5*cos(#n*2*pi/11) y:5*sin(#n*2*pi/11)
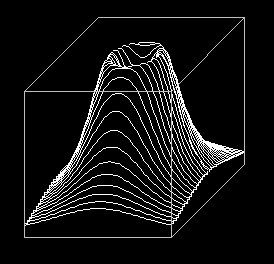
Grafici e figure 3D
Se hai definito una funzione F a 2 input e 1 output, ad es. F(x,y)=1/SQR(x^2+y^2), puoi tracciarne il grafico, ad es. in
3D(F, -3,3,-2,2, 30,20, 1/2,1/2)
il grafico (vedi figura A) viene rappresentato in prospettiva parallela (proiettato sul piano yz); la coppia 1/2,1/2 indica che la direzione della proiezione è quella del vettore (1,1/2,1/2): in pratica se in fondo al comando si mette p,q si ottiene la prospettiva da cui il punto (1,p,q) si vedrebbe sovrapposto all'origine degli assi. La coppia 30,20 indica le parti in cui vengono suddivisi gli intervalli delle x e delle y, da cui dipende il numero delle facce piane della figura che approssimerà il grafico di F. Cliccando 2 volte [o] si ottimizza la visione. Col comando:
3DB(F, -3,3,-2,2,0,5, 30,20, 1/2,1/2)
dove B sta per "box", si comanda anche il tracciamento del parallelepipedo di "base"
X[]=3,0,0,0,0
Y[]=0,0,2,0,0
Z[]=0,0,0,0,5
3db(F+4, -3,3,-2,2,0,5, 30,20,1/2,1/2)
si ottiene C: si è comandato di aggiungere al grafico di F la figura P(0)-P(1)...P(4) ottenuta congiungendo i punti
X[5]=S; Y[5]=15
FOR #I=0 TO 100:X[6+#I]=COS(2PI/100*#I); Y[6+#I]=SIN(2PI/100*#I); Z[6+#I]=1
3db(F+106, -3,3,-2,2,0,5, 30,20,1/2,1/2)
si ottiene D: alla figura che forma gli assi si è aggiunto un salto con cambio colore e poi il cerchio di raggio 1 centrato nell'asse z e posto nel piano z=1. Col comando:
3D(106,1/2,1/2)
si ottiene E: si traccia solo la figura P(0)-P(1)...P(106). Non si mette il dominio e in fondo si indica solo la direzione della proiezione. In F è riprodotto che cosa si ottiene cambiando la direzione nel modo seguente:
3d(106,-1/4,2).
In F è evidenziato anche il punto (0,0,1), cosa ottenuta con (vedi sopra):
SHOW3D(0,0,1)
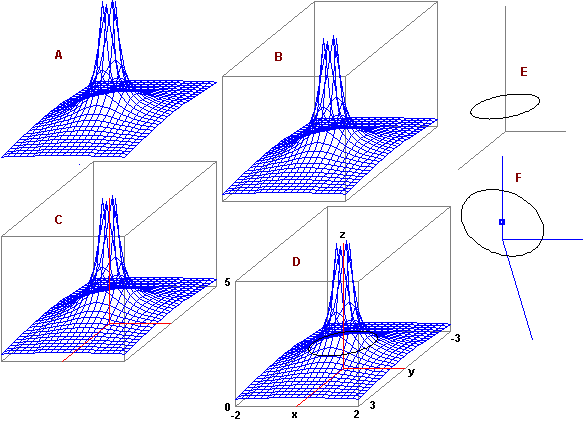
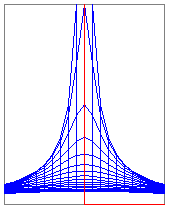
L'ultima figura rappresenta come si vedrebbe il grafico di F con la direzione (1,0,0), ossia mettendo 0,0 in fondo al comando 3d (è la proiezione perpendicolare al piano yz, ossia diretta come l'asse x).
Usando 3D | colore o 3DB | colore al posto di 3D e 3DB si può assegnare un particolare colore al grafico. Altrimenti si può, poi, cambiare il colore standard.
E S E M P I
[indice]
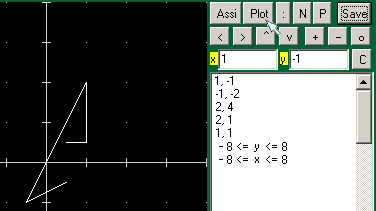 | Si sta tracciando una poligonale iniziata nel punto (1,1). Si è appena tracciato il punto (1,-1). Nella finestra destra appaiono la scala (o, meglio, il rettangolo cartesiano che viene associato alla finestra-grafici) e i punti man mano introdotti. |
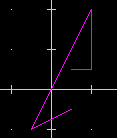 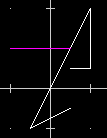 | Se invece di un punto batto C (come x) e 13 (come y) viene impostato il colore 13 (magenta); vedi fig. a sinistra. Se invece batto S e 13 viene introdotto un salto e solo quello che segue (nel caso della figura a destra si tratta del segmento ottenuto introducendo -2,2 e 1,2) viene tracciato col colore 13. |
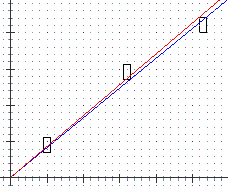
| La possibilità di introdurre come x e y intervalli, nella forma a..b, e ottenere il tracciamento di rettangoli facilita la costuzione di istogrammi: vedi fig. sotto a sinistra. A destra è esemplificato l'uso di questa opzione per la rappresentazione dei dati sperimentali di una relazione del tipo y=kx per la ricerca di k attraverso l'individuazione dei segmenti con masssima e minima pendenza tra quelli con un estremo in (0,0) che passano per tutti i rettangolini. | |
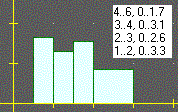 |  |
| [l'immagine è stata ottenuta non salvando il grafico con Save, ma azionando Alt+Stamp (con la finestra dell'applicazione attiva) e incollando in Paint la finestra, in modo da poter copiare dalla sottofinestra destra e incollare a fianco al grafico le coordinate dei rettangoli dell'istogramma; in alternativa potevo inserire le scritte col comando "scrivi", e usare Save] | |
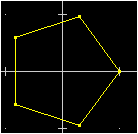 | La figura a lato (pentagono regolare inscrivibile in un cerchio di raggio 2) è stata ottenuta introducendo i vertici espressi usando le funzioni circolari [battendo via via nel box-x e nel box-y 2cos(0),2sin(0); .. ; 2cos(72*5gr),2S(72*5gr); non si è riscritto tutto: man mano si è modificato solo il fattore moltiplicativo e premuto su Plot].
Questo è anche un esempio d'uso di coordinate polari; per introdurre ρ,θ introduco x=ρcos(θ), y=ρsin(θ). Per ottenere la figura a lato, in alternativa potevo usare IMP con nel box P5 (poligono regolare a 5 lati: vedi sopra) e poi azionare Scala con 2 in Mx e My. [potrei anche usare il ciclo for #i=0 to 5: plot x:2*cos(#i*360/5gr) y:2*sin(#i*360/5gr)] |
| A destra è illustrata la importazione del file cur.gfu (ottenuto con GraFun.bas, come curva descritta in forma parametrica), collocato nell'unità C (in nessuna cartella; se fosse stato nella sottocartella Pippo di Documents and Settings avrei potuto mettere nel box |  |
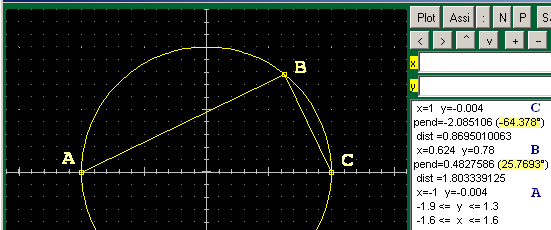
| Se (vedi) clicco su un punto della finestra grafica e, poco dopo, su un altro
punto tenendo premuto il tasto Alt, viene temporaneamente evidenziato il segmento che
li congiunge e vengono scritte nella finestra di lista anche lunghezza, pendenza e
inclinazione del segmento. Ad esempio nel caso della figura seguente riusciamo
a capire che l'angolo ABC è di (circa) 90°: da A a B l'inclinazione
è di 26°, da B a C è di -64°, per cui da BA a BC c'è
una rotazione di 90°. Ovvero, potevo fare il prodotto delle loro pendenze col
comando
|
 |
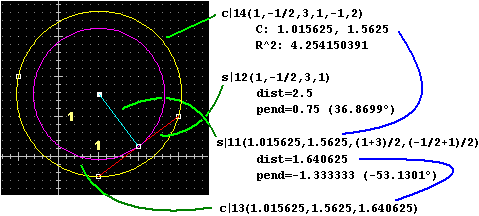
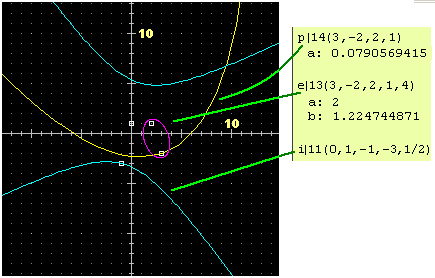
| Esempi di tracciamenti di coniche e segmenti (vedi): i comandi usati e i valori che compaiono sulla finestra-appunti. |
  |
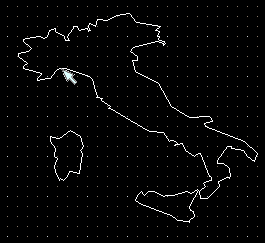
| A destra è riprodotto il goniometro ottenuto nel modo indicato sopra. Sotto sono riprodotte altre figure. Quella ottenuta scrivendo le coordinate geografiche di un po' di punti del contorno dell'Italia (cliccando con il mouse si possono ottenere le coordinate geografiche). Quella ottenuta importando il file generato con un programma per lo studio di funzioni in due variabili: il programma Poligon può essere usato per realizzare grafici mediante altri programmi senza doversi preoccupare di utilizzare in questi specifiche istruzioni grafiche. | 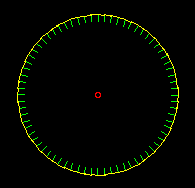 |
  | |
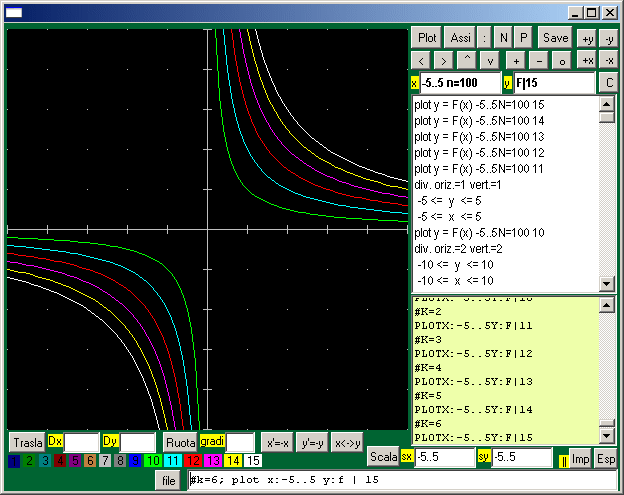 |
| Il fascio soprastante è stato ottenuto direttamente in Poligon. La cosa è realizzabile cambiando man mano la definizione di F, riprendo [Imp], cambiando il codice colore nel box Y e ripremendo [Plot]. In alternativa si può introdurre una costante nella definizione di F e modificare via via il colore di default: F(x) = #K/x, [Imp] color 15; #K = 1 [Imp] azionare [Plot]. Poi modificare il colore e la def. di #K: color 14; #K = 2 [Imp] e riazionare [Plot]; poi … Oppure introdurre anche il comando Plot da tastiera: #k=1; plot x:-5..5 y:f | 10 e via via modicare questa riga di comandi e premere Enter [oppure usare: FOR #k=1 TO 5: plot x:-5..5 y:f | 10+#k |
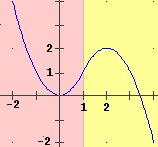
| Ecco come definire (a tratti) la funzione: F: x  x2 se x < 1, F: x x2 se x < 1, F: x  2-(x-2)2 altrimenti, 2-(x-2)2 altrimenti,rappresentata graficamente a fianco: (vedi qui per le "funzioni" < e ≥) |
 | ||
 | Ecco un trucco per restringere il dominio di una funzione.
Qui voglio ottenere la funzione seno con il dominio privato dell'intervallo [1,3).
Definisco D che valga 1 nel nuovo dominio e 0 altrove, e poi F nel modo sotto illustrato [a sinistra il grafico di F tra -3 e 5]. D(x) = 1-(x>=1)*(x<3) F(x) = SIN(x)*D(x) + 0/D(x) o, più semplicemente: F(x) = SIN(x)/D(x) | ||
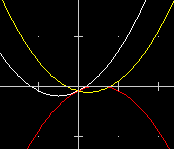 | I grafici di una funzione polionomiale al variare dei coefficienti: F(X)=(((#A * X) + #B) * X) + #C (modo veloce per introdurre una funzione polinomiale, senza usare ^) Azioni [Imp] e [Plot] con: #A=1; #B=2; #C=-1 #A=1; #B=-1; #C=-1 #A=-1; #B=2; #C=-1. |
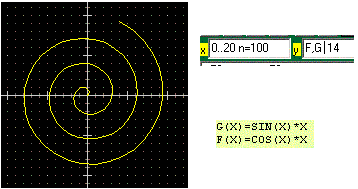 La figura a destra è un dodecagono realizzato come curva in forma parametrica con: x[ 0..360 n=12 ] y[ F,G | 10 ] dopo aver definito F(x) = SIN(x*gr), G(x) = COS(x*gr). | La figura a sinistra è una curva costruita in forma parametrica direttamente in Poligon.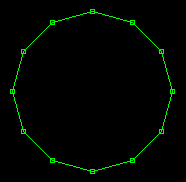 |
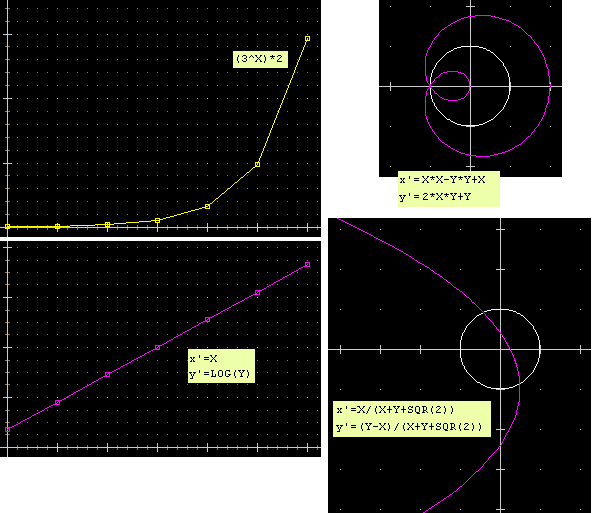
| Alcune trasformazioni geometriche: – il grafico di y = 2·3x, fatto tracciare su punti a ascissa intera, e del suo trasformato secondo y'=log(y); – il cerchio di centro (0,0) e raggio 1 e il suo trasformato mediante z' = z2+z (z = x + iy, z' = x' + iy', x' = x·x-y·y+x, y' = 2·x·y+y); [invece di mettere =x*x-y*y+x nel box X e =2*x*y+y nel box Y si potevano mettervi, usando le abbreviazioni rho e theta, =rho^2*cos(theta*2)+x e =rho^2*sin(theta*2)+x; infatti z*z ha modulo al quadrato e argomento raddoppiato rispetto a z] – lo stesso cerchio e il suo trasformato con x' = x/(x+y+√2), y' = (y-x)/(x+y+√2). | |
 | |
– un altro esempio: il cerchio goniometrico (tracciato col comando C) e traslato di (1/2, 1/2) (figura A) e la figura (B) ottenuta da A con la trasformazione rappresentata in
forma complessa dalla funzione z  1/z realizzata mettendo 1/z realizzata mettendo[la immagine riprodotta a destra è stata sottoposta alla inversione dei colori]. | 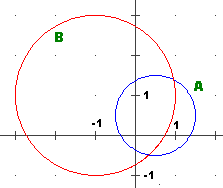 |
| – I grafici dei record di salto in alto dal 32 (1932) all'88 femminili e maschili distinti per la forma dei punti (come primo 'punto' in un caso è stato messo 'S,210' (codice di salto, tipo 2 di punti, colore 10), nell'altro 'S,114'), e quelli dei loro numeri indici: i grafici precedenti sono stati salvati con un certo nome, poi ciascuno e' stato richiamato e poi trasformato con y' = y/PrimoRecord*100 (ad es. per i record femminili si è messo =x nel box x e =y/165*100 nel box y); i file trasformati sono stati salvari con nuovi nomi, richiamati uno dopo l'altro e poi sovrapposti con un doppio clic su [P]; sotto ai grafici sono riprodotti il file dei record femminili e, a destra, che cosa appare sulla finestra di output se si trasforma questo file in quello dei numeri indici e se si fanno visualizzare i punti del nuovo file (se metto nella finestra di Imp punto(1), punto(2), ... e via via premo Enter, o clicco [Imp], ottengo le coordinate del primo, secondo, ... punto, ovvia il primo anno e il relativo numero indice, il secondo e ...). | ||
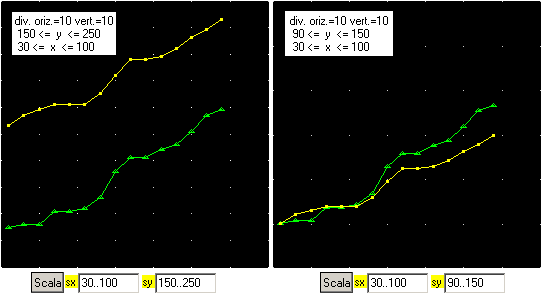 | ||
'record alto femmine dal 32 ogni 4 anni 16 s,210 32,165 36,166 40,166 44,171 48,171 52,172 56,176 60,186 64,191 68,191 72,194 76,196 80,201 84,207 88,209 | x'=X X y'=Y/165*100 32,100 36,100.6060606060606 40,100.6060606060606 44,103.6363636363636 48,103.6363636363636 52,104.2424242424242 56,106.6666666666667 60,112.7272727272727 64,115.7575757575758 68,115.7575757575758 72,117.5757575757576 ... | |
| Altre trasformazioni: – il grafico di una funzione (A) - una funzione polinomiale di grado 4 - e sue successive trasformazioni ottenute con: x'=X y'=(Y1-Y0)/(X1-X0) (x0 e y0 sono gli x e y precedenti, x1 e y1 sono i successivi) impostata mettendo =x nel box X e =(y1-y0)/(x1-x0) nel box Y oppure mettendo (solo) in Y =DERIV (che opera in modo più preciso: calcola e mette in Y la pendenza tra due punti successivi, mentre mette in X la media delle loro ascisse). | 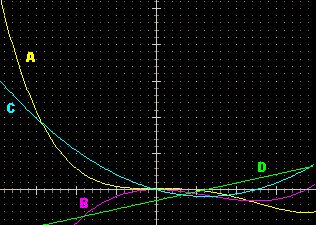 |
|
– il grafico della pioggia (in millimetri) mese per mese a Genova in più anni e la sua trasformazione mediante successive applicazioni di medie mobili (di ordine 3), ottenute con ripetuti [Plot] con: =(x+x0+x1)/3 in X e =(y+y0+y1)/3 in Y oppure mettendo (solo) in Y =MEDMOB | 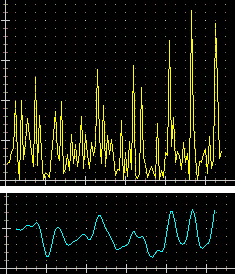 |
| – lo stivale italiano e la figura ottenuta con più applicazione di medie mobili, in questo caso realizzate con: in Y =MEDMOB1 in modo da conservare (e lasciare fissi) primo e ultimo punto. |  |
| – il grafico di y=f(x)=SGN(SIN(x)) tra -2*Pi e 2*Pi e quello della funzione continua G che passa per (-2*Pi,-1) che lo ha come pendenza; questo è stato ottenuto (dopo che era stato fatto l'altro grafico): tracciando il punto (-2*Pi,-1) e poi mettendo (solo) in Y =INTEGR che equivale ad azionare x'=X y'=(X-X0)*Y+% (Y è f(x), Y' è G(x), % sta per l'ultimo G(x) calcolato) [ G che abbia f come pendenza la si ottiene dal punto iniziale aggiungendo man mano DeltaG(x), pari a DeltaX*G'(x) = DeltaX*f(x)] | 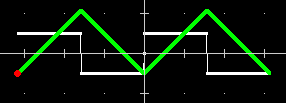 |
| – trasformazioni geometriche possono essere realizzate anche impiegando demo (vedi esempi più avanti). |
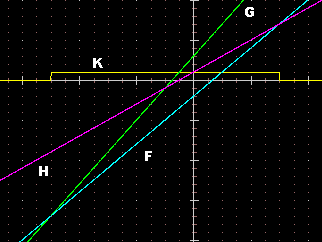 | Il grafico di K visualizza le soluzioni del sistema di disequazioni: H(x) > F(x) AND F(x) < G(x) F(X)=X*3-2 G(X)=X*4+3 H(X)=X*2+1 K(X)=((X*2+1)>(X*3-2))*((X*3-2)<(X*4+3)) e la ricerca dei valori (dove K "scavalca" y=0.5) [-10,0] K(X)=0.5 se x = -5 [0,10] K(X)=0.5 se x = 3 |
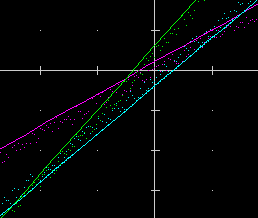 | La visualizzazione delle soluzioni (x,y) del sistema di disequazioni: y > F(x) AND y < G(x) AND y < H(x) (il triangolo intersezione dei 3 semipiani evidenziati con la puntegiatura generata usando RND) tracciando L(X)=X*3-2+RND M(X)=X*4+3-RND N(X)=X*2+1-RND |
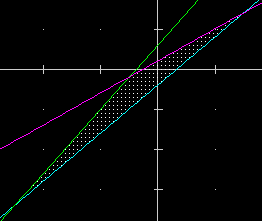 | ovvero tracciando w(x,y)=1 con: W(X,Y)=(Y >= (X*3-2))*(Y <= (X*4+3))*(Y <= (X*2+1)) |
| Per evidenziare la parte di piano compresa tra i grafici del seno e del coseno si è tracciata (senza congiunzione dei punti, ossia mettendo P dopo N=…) il grafico di H così definita: H(x) = COS(x) + ((SIN(x)-COS(x))*RND | 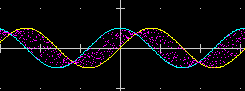 |
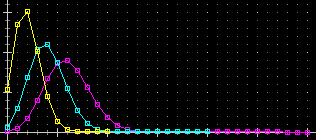 | I grafici delle binomiali p=0.2 e n=10, 20, 30. Sono state ottenute con f(x)=BINOM e [Imp] Si è ottenuto: F(x)=!(#n)/(!(#n-x)*!(x))*#p^x*(1-#p)^(#n-x) Si è posto #P=0.2 e #N=10; si è azionato [Plot] con 0..10 n=10 in X e F | 14 in Y Si è posto #N=20; si è azionato [Plot] con 0..20 n=20 in X e F | 11 in Y Si è posto #N=30; si è azionato [Plot] con 0..30 n=30 in X e F | 13 in Y Si è cliccato [:] per evidenziare i punti. Si poteva operare anche da tastiera modificando via via: #p=0.2; #n=10; plot x: 0..10 y: f | 11 |
| Se, invece, volessimo esportare in Stat dati che corrispondano alla distribuzione teorica binomiale per n = 10, p = 0.2, potremmo usare il demo qui a destra (che impiega un ciclo for, il comando stamp= e ") per generare la lista sotto a destra (contenente le frequenze attese - nel formato "dati già classificati" - nel caso si facessero tante prove quante i possibili esiti, 2n), che può essere copiata in Stat, da cui si può ottenere l'istogramma riprodotto, e confrontarlo con dati sperimentali: | #p=0.2; #n=10; F(x)=binom noscrivi=1 FOR #K=0 TO #N: #F=F(#K)*2^#N; #x=#k-1/2; STAMP=#x#F #x=#n+1/2; #f=0 stamp=#x#F " noscrivi=0 | |
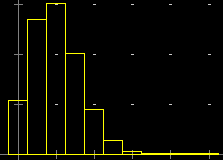 |
-0.5,109.9512 0.5,274.8779 1.5,309.2376 2.5,206.1584 3.5,90.19431 4.5,27.05829 5.5,5.637145 6.5,0.8053064 7.5,0.07549747 8.5,0.004194304 9.5,0.0001048576 10.5,0 | |
| Probabilità che lanciando un dado equo 10 volte si ottengano almeno 5 uscite multiple di 3: calcolo Pr(U=5)+...Pr(U=10) con U binomiale con n=10 e p=1/3 (la probabilità che in un lancio l'uscita sia 3 o 6 è 1/6+1/6 = 1/3): f(x)=BINOM e [Imp] F(x)=!(#n)/(!(#n-x)*!(x))*#p^x*(1-#p)^(#n-x) Aziono [Imp] con: #P=1/3; #N=10; [5,10] F SUM per calcolare F(5)+ … F(10). Ottengo: [5,10] F SUM = 0.2131280800690952 = 4195/19683 [arrotondando: 21.3%] |
La verifica che ∫[0,∞)e-x dx =1 (x  e-x è una funzione densità), il calcolo della sua media (1), e del suo scarto quadratico medio (1) [è un esempio d'uso in un caso in cui i calcoli sarebbe facile farli simbolicamente] e-x è una funzione densità), il calcolo della sua media (1), e del suo scarto quadratico medio (1) [è un esempio d'uso in un caso in cui i calcoli sarebbe facile farli simbolicamente]F(X) = EXP(-X) [0,10] F INT = 0.9999546001 (introduco [0,10] f int) [0,20] F INT = 0.9999999979 [0,40] F INT = 1 G(X) = X*EXP(-X) G Int[0,40] = 1 H(X) = ((X-1)^2)*EXP(-X) [0,40] H INT = 1 (introduco [0,40] h int) |
| Calcolo l'integrale tra -σ e σ della densità gaussiana per diversi valori di μ e di σ. Aziono [Imp] con: f(x)=gauss ottenendo: F(X)=1/(sqr(2pi)*#s)exp(-(x-#m)^2/(2*#s^2)) Per calcolare ∫[-σ,σ]F per σ=1 e μ=0 imposto: #S=1; #M=0; [-#S,#S] F int ottenendo 0.6826894923 Per calcolarlo per σ=2 imposto: #S=2; [-#S,#S] F int ottenendo 0.6826894923 ... |
| Il vertice della parabola che è grafico di F così definita:
F(X) = (1+X)*(X-3/7) [-5,5] F MIN [Imp] se x = -0.285714285761179 = -2/7 y = -25/49 | 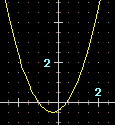 |
| Se in figura.txt ho messo una figura dipendente da 3 parametri (un parallelogramma in cui: #L è un lato, #H è l'altezza ad esso relativa, #A è l'angolo formato con esso dall'altro lato): 5 0, 0 #L, 0 #L + #H / tan(#A*gr), #H #H / tan(#A*gr), #H 0, 0 ecco come posso rappresentarla per diverse scelte di essi (importando il file e definendo i parametri con un'unica riga di comandi): #L=2; #H=3; #A=120; c:\figura.txt #L=2; #H=3; #A=60; c:\figura.txt #L=2; #H=3; #A=45; c:\figura.txt #L=2; #H=1.5; #A=45; c:\figura.txt |
 |
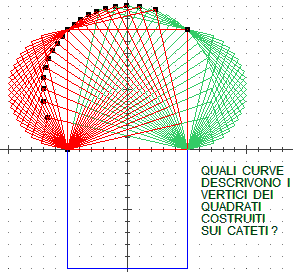
| Una figura, prova.txt, più complessa dipendente da un solo parametro (che illustra il teorema di Pitagora) rappresentata usando anche simboli di funzione non predefiniti. Il triangolo rettangolo è inscritto nel semicerchio di centro (0,0) e raggio 1 che sta nel semipiano y≥0. 18 s, 14 -1, 0 1, 0 1, -2 -1, -2 -1, 0 s, 13 -1, 0 #X, f(#X) [vertice superiore del triangolo] g(#X), h(#X) [un vertice del quadrato sinistro] k(#X), l(#X) [un vertice del quadrato sinistro] -1, 0 s, 12 1, 0 #X, f(#X) m(#X), n(#X) [un vertice del quadrato destro] o(#X), p(#X) [un vertice del quadrato destro] 1, 0 dove: F(X)=SQR(1-(X*X)) G(X)=X-SQR(1-(X*X)) H(X)=(X--1)+SQR(1-(X*X)) K(X)=-1-SQR(1-(X*X)) L(X)=X--1 M(X)=X+SQR(1-(X*X)) N(X)=(1-X)+SQR(1-(X*X)) O(X)=1+SQR(1-(X*X)) P(X)=1-X | |
 | |
| figure ottenute con: #X = -1 ; c:\prova.txt #X = -0.5 ; c:\prova.txt ... Un'alternativa è presentata nel demo pitagor2.dm, presente nella banca di file, che produce in modo animato la figura a lato: memorizzare le coordinate della figura in variabili indiciate e usare il comando |
 |
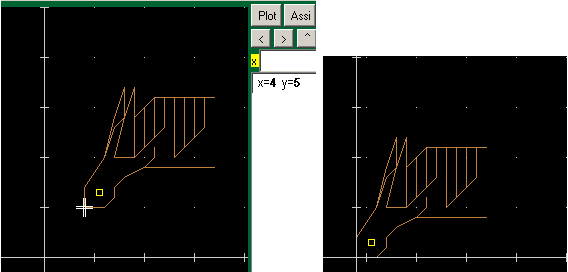
| Qui si sono inserite delle scritte. Con font- si è ridotta la dimensione dei caratteri; con legenda=1 si è fatta visualizzare sul grafico la porzione di piano cartesiano rappresentata; con scrivi si sono inserite etichette per due punti, collocate una poco sopra, una poco a destra. Il tracciamento dei punti è stato comandato da tastiera (usando il box "file") invece che con il mouse (e i box "x" e "y"). Col comando FILL si è poi colorata la parte della figura contenente il punto (2.1,1.1) del colore "12" prendendo come confine le parti di colore "15" (nel nostro caso il poligono era di colore 15 e se ne è riempita la parte contenenete il punto scelto). | |
|
font- legenda=1 assi plot x:1 y:4 plot x:2 y:4 plot x:2 y:1 plot x:3 y:1 plot x:1 y:3 plot x:1 y:4 scrivi 2,4.2:A scrivi 3.3,1:B fill 2.1,1.2: 12|15 |
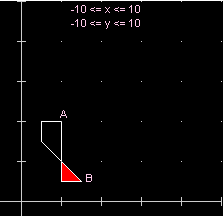 |
| Un rettangolo ruotato attorno a (-1,1) e sottoposto a una particolare trasformazione di scala (i comandi qui sono stati dati da tastiera). L'area non è cambiata (si ottengono 8 e 8), il perimetro (lung) sì (si ottengono 12 e 18.3588989). | |
|
plot x:2..4 y:1..5 area lung ruota gradi:60 dx:C-1 dy:C1 scala sx:2 sy:0.5 area lung |
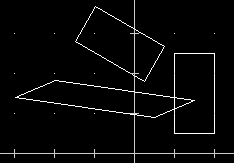 |
 | La determinazione del centro di una figura e la sua evidenziazione con un sistema di assi (quello qui trovato è il centro dell'Italia peninsulare, rispetto al piano cartesiano costituito dalle coordinate geografiche e dotato della distanza euclidea - la ordinata è leggermente maggiore di quella dell'effettivo centro geografico in quanto, sulla superficie terrestre, lungo i paralleli, il rapporto tra distanza reali e differenza di longitudine diminuisce avvicinandosi ai poli). |
| Quelli che seguono son due esempi di Demo che calcolano il massimo comune divisore e il minimo comune multiplo dei due numeri naturali messi in #M e #N. Il primo usa "altre variabili", il secondo non ne usa altre (se definisco #m e #n, copio da qui le righe del demo e dò il comando CLIP, il demo viene eseguito automaticamente e ottengo i risultati) | 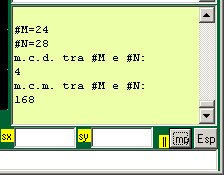 |
|
A lato un demo per calcolare il fattoriale esatto di un numero naturale,
che sfrutta l'operatore [*] (vedi) per eseguire le moltiplicazioni
esatte tra numeri naturali; sotto l'esito (fino a 50! Poligon calcola esattamente i fattoriali,
poi impiega una funzione approssimante, che dà luogo a risulati
con quasi 6 cifre signficative: vedi, più sotto, il valore che si otterrebbe
col calcolo diretto di 60!; per visualizzare tutte le cifre memorizzate in #F si deve usare #F:, non #F=, che arrotonderebbe a
15 cifre). #F = 83 209 871 127 413 901 442 76 341 183 223 364 380 754 172 606 361 245 952 449 277 696 409 600 000 000 000 000 !(60) = 8.320979201525224E81 #F = 8.32098711274139E81 | #n=60 ' metti in #N un numero naturale, copia le righe ' seguenti, aziona CLP: ottieni il fattoriale noscrivi=1 tempo 0 #i=0 #f=1 label 0 #i=val(#i+1) #f=#f[*]#i goto 0 if #i<#n noscrivi=0 #f: ---Qui un demo per calcolare la divisione intera tra numeri naturali comunque grandi. |
| Mentre lavoro con Poligon posso decidere di costruire una figura come file usando BloccoNote/NotePad (o un altro editor), di salvarla (senza chiudere BloccoNote), caricarla con Poligon, vedere l'esito, modificare il file da BloccoNote e risalvarlo, ricaricare la figura. Analogamente si possono costruire e caricare demo.. Si clicca [file] dalla finestra di dialogo e si seleziona la cartella in cui si vuole costruire il file. Si clicca (col pulsante destro) all'interno della finestra di dialogo col pulsante destro per costruire un nuovo file-di-testo, e si cambia il nome del file come si preferisce. Nell'esempio seguente il nome è stato cambiato in "prog.dm". Poi, sempre col pulsante destro, si apre il file con BloccoNote e lo si completa come si crede. | |
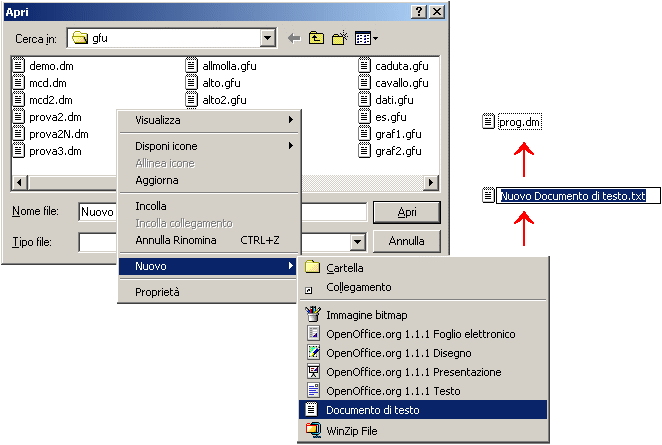 | |
| Nota. Usando Windows conviene sempre impostarlo in modo che nelle cartelle si vedano le estensioni di tutti i file, ossia che i nomi dei file vengano visulizzati come "macosa.txt", "macosa.doc", …, altrimenti potrebbe accadere che un file appia con una estensione mentre ne abbia due di cui una nascosta (uno pensa di avere creato "figura.gfu" mentre in realtà ha "figura.gfu.txt"). Se l'opzione non è attivata puoi farlo operando sul PannelloDiControllo (puoi accedervi dal menu Start/Avvia, in genere in basso a sinistra). Occorre arrivare alle OpzioniCartella (per arrivarci potrebbe essere necessario passare attraverso una cartella più generale del tipo OpzioniDiVisualizzazione) e togliere con un clic il segno di spunta dal box NascondiEstensioni. Tieni inoltre presente che per visualizzare tutti i file nelle finestre di dialogo dei menu File di una applicazione devi selezionare AllFiles/TuttiIFile nel box "Tipo di file", altrimenti, per es., con un browser (InternetExplorer, Netscape, …) vedresti solo i file con estesione .htm o .html e con BoloccoNote solo i file con estensione 'txt'. Analogamente, se salvi da BloccoNote un file di estensione, ad es., 'gfu' o 'dm' cambiandone il nome, se nel box "Salva come" lasci 'documenti *.txt' invece di selezionare 'Tutti i file', viene aggiunta automaticamente l'estensione 'txt'. |   |
| Ecco ad esempio che cosa potrebbe fare una persona che, analizzando i dati sulle piogge mensili a Genova visti in un
esempio precedente volesse trovare i mesi in cui non è piovuto e contare quanti sono: può, senza uscire da Poligon, costruire (usando la finestra di dialogo che si apre con [file]) un demo in cui inserire i comandi a fianco, salvarlo con un certo nome e importarlo in Poligon. Ottiene le uscite riportate a destra. Se vuole ottenere l'esplicitazione di anno e mese può inserire nel demo: … punto(#i) noscrivi=1 =(%1\12)+1 "anno "out =(%2 mod 12)+1 "mese "out #m=#m,1,+ … |
numpunti noscrivi=1 noplot=1 tempo 0.02 #n=% #i=0 #m=0 LABEL0 #i=val(#i+1) punto(#i) goto 1 if % > 0 noscrivi=0 punto(#i) noscrivi=1 #m=val(#m+1) LABEL1 goto 0 if #i < #n =#m noscrivi=0 noplot=0 "mesi senza pioggia "out |
|
| Un esempio di composizione di funzioni: [si è anche evidenziata la struttura di K(x), e che è la stessa nel caso in cui K fosse stata definita direttamente senza usare F, G e H] | 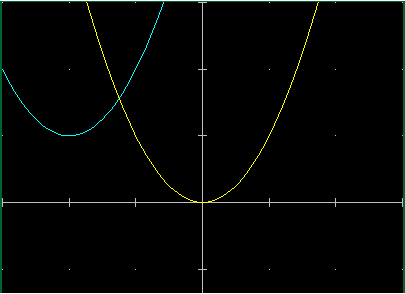 | F(X)=x^2 G(X)=x+2 H(X)=x+1 K(X)=H(F(G(x))) plot x:-3..3 y: f | 14 plot x:-3..3 y: k | 11 K(x): v0 = x + 2 v1 = v0 ^ 2 v2 = v1 + 1 K(X)=(x+2)^2+1 K(x): v0 = x + 2 v1 = v0 ^ 2 v2 = v1 + 1 |
| Per definire: | G(X)=SQR(xx+3x+2) F(X)=3G(x)/(1+G(x)) | |||
| ||||
| può essere comodo procedere nel modo indicato a fianco: usando un simbolo ausiliario possiamo correggere più facilmente eventuali errori. Si noti che abbiamo dimenticato di mettere alcuni "*". Poligon, in casi come questo, corregge automaticamente l'errore. | ||||
| Si possono costruire, e memorizzare, dei demo per l'esecuzione di alcune operazioni di uso frequente. Qualche esempio è già scaricabile da rete (o dal computer se vi si è scaricato Gli Oggetti Matematici). Ad es. nel caso si voglia tracciare la retta tangente in un punto a un grafico di una generica funzione si può caricare il demo diff.dm. Prima di caricarlo possiamo aprirlo (cliccando dalla finestra di dialogo di [file] sul suo nome col pulsante destro) e leggerere i commenti: 'Il demo mette in P la funzione che ha per grafico la tangente a y=F(x) in (#x,F(#x)) 'L'utente deve definire F e assegnare #x e il passo iniziale #h (con #x+#h nel dominio) 'Il demo usa (oltre a F, #x, #h) w[] ' w[4] funge da DeltaX (#h iniziale rimane invarato), w[1] da f'(x0) 'Se fai il grafico di F e poi quello di P ottieni la retta tangente 'Il demo non funziona per i punti agli estremi dell'intervallo di definizione | 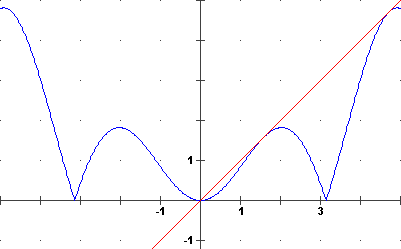 |
Se voglio trovare la tangente al grafico di  |x sin(x)| |x sin(x)| w[1](x-#x)+w[0] w[1](x-#x)+w[0]Per trovare le derivate da destra/sinistra di F in π (in cui si ha un punto angoloso) definisco come D(x) il rapporto incrementale (F(#x+x)-F(#x)) / x e pongo #x=pi. | |
Poi, calcolo ad es. D(10^-1), D(10^-2), D(10^-3), ... ottenendo le uscite a lato, dalle quali deduco che posso assumere 3.1415926536 come valore della derivata da destra (arrotondo l'ultima uscita in cui le variazioni sono state "regolari", prima dell'intervento di errori dovuti al fenomeno della "cancellazione delle cifre"). Analogamente, con D(-10^-1), D(-10^-2),... potrei determinare la derivata da sinistra (che in questo caso sarà, ovviamente,  x sin(x) x sin(x) |
D(10^-1)=3.136359283204442 D(10^-2)=3.141540293973926 D(10^-3)=3.141592129990312 D(10^-4)=3.141592648356588 D(10^-5)=3.141592653519542 D(10^-6)=3.141592653643674 D(10^-7)=3.141592644601108 D(10^-8)=3.141592596024711 D(10^-9)=3.141592528804902 D(10^-10)=3.141589066312010 |
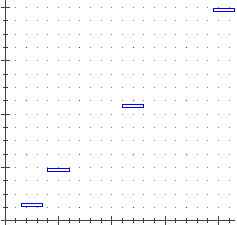
| Se vuoi preparare un file contenente dati del tipo: x +/- Dx, y +/- Dy ossia coppie di dati sperimentali dotati di precisione, puoi usare un file DM come quello a lato, in cui i dati sono introdotti come intervalli di indeterminazione. |
plot x:9-1..9+1 y:20-1..20+1 plot x:17-1..17+1 y:31-1..31+1 plot x:22-1.5..22+1.5 y:38.21..40.17 |
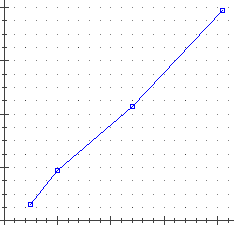
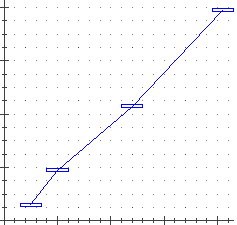
| Se hai già introdotto i dati senza precisione (ottenendo il grafico sotto a sinistra) e vuoi associare la stessa precisione a tutte le "x" e la stessa precisione a tutte le "y", puoi usare un opportuno demo, come il seguente (aggprec.dm), in modo da ottenere (avendo assegnato opportune precisone #x alle x e #y alle y) la seconda figura. La terza figura è stata ottenuta con un doppio [P]. | |
| |
' se la figura attuale rappresenta dati (x,y) e se in #x metti ' un numero positivo e in #y un altro, ottieni la rappresentazione ' dei "dati dotati di precisione" (x +/- #x, y +/- #y) tempo 0.02 noscrivi=1 n numpuntip #n=val(%) #i=1 label0 puntop(#i) plot x:%1-#x..%1+#x y:%-#y..%+#y #i=val(#i+1) goto 0 if #i<#n+1 oo noscrivi=0 --------
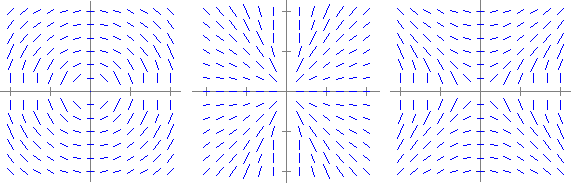
'Il demo traccia il campo direzionale di y'=F(x,y) 'L'utente deve definire F, definire il rettangolo [a,b]*[c,d] in cui 'tracciare le direzioni delle soluzioni e i numeri M e N (>0) delle 'parti in cui suddividere [a,b] e [c,d] 'Il demo usa (oltre a F, #a, #b, #c, #d, #m, #n) #h, #k, #i, #j, #p 'Ti conviene all'inizio provare con #M e #N piccoli (ad es.= 8): al raddoppiare 'di #m e #n il tempo quadruplica.consente di tracciare il campo direzionale di una equazione differenziale. Ecco che cosa si ottiene con:
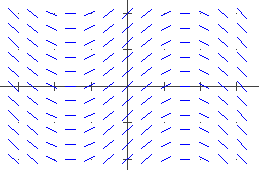
'Il demo traccia la curva soluzione di y'=F(x,y) in [a,b] (o [b,a] se a>b) 'tale che y(a)=#y 'L'utente deve definire F e assegnare #a, #b e #y, e il numero #N dei passi 'Il demo usa (oltre a F, #a, #b e #n) #x, #p e #i 'In casi senza grandi oscillazioni basta #n=30. Comunque puoi provare con '#n crescente. Se vuoi cambia il codice colore (nel primo PLOT) (e salva) tempo 0 noscrivi=1 noplot=1 noimp=1 plot x:s y:14 ...con #a=1, #b=-1.5, #y=1.5:
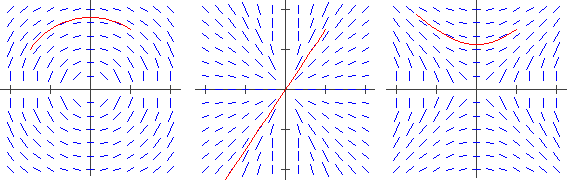
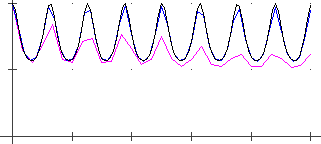
| Voglio studiare ∫1∞sin(x)/x2 dx. Posso definire: | F(X) = sin(x)/x^2 #x=1 |
| e poi costruire un demo con i seguenti comandi
(attraverso cui calcolo | |
tempo=0.01 #n=0 #i=0; #a=#x label5 noscrivi=1 [#a,#a+2^#n] f int noscrivi=0 #i=val(#i+%) #a=val(#a+2^#n) noscrivi=1 #n=val(#n+1) goto 5 in #n<10 noscrivi=0 |
Ottengo: #I=0.472399177000000003 #A=2 #I=0.552285987600000028 #A=4 #I=0.502831163400000003 #A=8 #I=0.507860828869999947 #A=16 #I=0.503223801289999995 #A=32 #I=0.503964534068999992 #A=64 #I=0.504108650106000034 #A=128 #I=0.504067787898600073 #A=256 #I=0.504070863048050044 #A=512 #I=0.504066120385240013 #A=1024 | L'ultimo è l'integrale tra 1 e 1024. Si può congetturare (la dimostrazione sarebbe comunque facile in questo caso) che l'integrale studiato converge, e approssimare con 0.50407 il suo valore. |
| Oppure si potrebbe ricorrere direttamente a un ciclo FOR senza costruire un demo:
dopo avere definito F e aver battuto #a=1; #b=20; #i=0, battere: for #N=1 to 2000:#y=[#a,#b] f int;#i=val(#i+#y);#a=val(#b);#b=val(#b+20);stamp=#a;stamp=#i;" (si sono scelti incrementi di 20, con ordine di grandezza non molto maggiore dell'ampiezza dell'oscillazione di F, in modo che le approssimazioni siano migliori) ottenendo: | |
|
20 0.502839620215645877 ... 40 0.504459240790899099 16040 0.504067059716576726 60 0.504333995547601055 16060 0.504067058090975184 80 0.504088168925645230 16080 0.504067060979396242 | |
| Ci si è fermati posizionando il mouse su [ESC], se no il ciclo avrebbe proseguito fino a [1,40000]. Possiamo prendere come valore 0.50406706 | |
| Un metodo più "efficiente" in questo caso consiste nel prendere come estremi destri di integrazione multipli dispari di π, ad es. così #a=1; #b=7Pi; #i=0 for #N=1 to 2000:#y=[#a,#b] f int;#i=val(#i+#y);#a=val(#b);#b=val(#b+7/Pi);stamp=#a;stamp=#i;" | |
1011.59283445591456 0.50406608470082592 1033.58398303104304 0.504067997971492928 .. 5013.9818751293088 0.504067022129250688 5035.97302370443712 0.504067101337040832 ... 16097.5207569943616 0.50406705804740224 16119.5119055694912 0.504067065755008384 | In questo modo (compiendo F una oscillazione ogni 2π) si alternano approssimazioni per eccesso e per difetto dell'integrale cercato. Ad es. dalle prima coppia di uscite riportata a sinistra abbiamo per il valore cercato I: 0.504066≤I≤0.504068, ovvero l'approssimazione 0.5040067. Dalla seconda coppia abbiamo: 0.50406702≤I≤0.50406710, e l'approssimazione 0.50406706. Dalla terza 0.504067058≤I≤0.504067066, e l'approssimazione 0.504067062. Andando avanti si potrebbe ottenere 0.504067061907. |
| A destra, come si potrebbe calcolare direttamente la frequenza relativa usando sum. L'evento preso in considerazione è lo stesso di sopra. Sotto il calcolo del valore atteso. |
#E=(INT(RND*6)+INT(RND*6)+2)>7 F(X)=#E/#N #N=1000; [1,#N] F SUM #N=2000; [1,#N] F SUM #N=10000; [1,#N] F SUM #N=50000; [1,#N] F SUM ... si ottengono: 0.4050000000000003 0.4040000000000003 0.4136999999999708 0.4167400000001352 ... |
(1-1/6)/2= 0.4166666666666667 =5/12 | |
| A destra, la stima del rapporto tra il volume di un cilindro e quello di un cono di eguali basi ed altezza
generando punti a caso nel parallelepipedo [-1,1] x [-1,1] x [0,1] e calcolando la frequenza con cui stanno sotto
al grafico di z = 1-√(x^2+y^2) (4 è il volume del parallelepipedo, 4·Frequenza è la stima del volume del cono, π è il volume del cilindro). Il valore atteso è 3. |
#X=RND*2-1; #Y=RND*-1; #Z=RND #E=#Z<(1-SQR(#X^2+#Y^2)) F(X)=#E/#N #N=10000 #f = [1,#N] F SUM PI/(#f*4)= 2.99655919 |
| Un esito del demo sistdiff.dm per risolvere numerico-graficamente sistemi differenziali. Qui si tratta di un modello preda-predatore. A sinistra le due funzioni y=y(x) e z=z(x) soluzioni. A destra il grafico della relazione tra di esse nel piano y,z (si ottiene una curva chiusa in quanto le due soluzioni sono periodiche con lo stesso periodo). | |
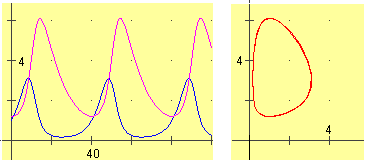 | |
|
| Un esito del demo ediff2.dm per risolvere numerico-graficamente equazioni differenziali del 2° ordine derivato dal demo precedente. Qui si tratta di un moto oscillatorio smorzato. A sinistra il grafico della funzione y=y(x) soluzione. A destra il grafico della relazione tra y e y'.(si ottiene una curva a spirale in quanto sia y che y' al tendere di x all'infinito tendono a stabilizzarsi - in questo caso entrambe su 0). | |
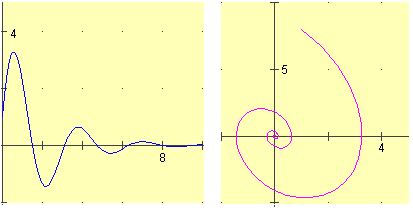 | |
|
| Il modo più comodo per realizzare trasformazioni geometriche è quello (vedi) di usare Plot con x' e y'. Ma in casi particolari può essere comodo memorizzare le figure (se hanno al più 200 punti) in variabili indiciate e trasformare queste mediante un demo. L'esempio seguente traccia un cerchio col comando C, ne copia i punti in una coppia di variabili indiciate e lo sottopone a due successive trasformazioni (x'=x+1, y'=y+1; x'=x·y, y'=(y-x)3), realizzando le figure a fianco. | 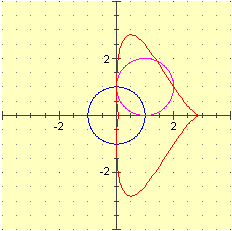 |
noscrivi=1 nolista=1 legenda=1 tempo=0 color 14 c numpunti #N=val(%) #i=0 label 1 #i=val(#i+1) punto(#i) x[#i-1]=%1 y[#i-1]=% goto 1 if #i<#n for #i=0 to #n-1: x[#i]=x[#i]+1; y[#i]=y[#i]+1 plot x:s y:10 for #i=0 to #n-1: plot x:x[#i] y:y[#i] for #i=0 to #n-1: #x=val(x[#i]); x[#i]=x[#i]*y[#i]; y[#i]=(y[#i]-#x)^3 plot x:s y:11 for #i=0 to #n-1: plot x:x[#i] y:y[#i] nolista=0 noscrivi=0 ---- | |
| Qualche esempio di calcolo matriciale: (1) generazione casuale di una matrice, inversione e calcolo di determinanti; (2) costruzione di una matrice e somma della matrice identità; (3) un demo per risolvere un sistema lineare A×X=B con X=A-1×B (si ottengono, per k=1, 6, 0 e -2, per k=-2, 4/3, 11/3 e 7/3); (4) un demo, che usa "" per stampare la riga 2 della matrice identità 5×5 (si ottiene la stampa di 0 1 0 0 0); in alternativa si poteva battere direttamente un ciclo for contenente stamp: FOR #J=1 TO 5: #I = VAL(I[2,#J]); STAMP = #I e poi "; (5) come, con una assegnazione e un doppio ciclo for, trasferire gli elementi di una matrice in una variabile a un indice (con x[](8)= si ottiene la stampa di x[0],...,x[8]). |
|||
(1)A[](3,3)=RND A[](3,3)= -7 -4 3 -4 -5 -1 2 -5 -4 A[](2,2)= -7 -4 -4 -5 A[](1,3)= -7 -4 3 DET(A)(3)=57 DET(A)(2)=19 B[](3,3)=INV(A) DET(B)(3)=1/57 | (3) | tempo=0 "soluzione di " x+2y+k*z=4 " 2x-y+3z=6 " k/2*x+z=1 "per k=1 e k=-2 #k=1 A[](3,3)=1,2,#k,2,-1,3,#k/2,0,1 B[](3,1)=4,6,1 C[](3,3)=INV(A) C[](3,1)=C*B(3) "x, y, z: C[](3,1)= #k=-2 A[](3,3)=1,2,#k,2,-1,3,#k/2,0,1 C[](3,3)=INV(A) C[](3,1)=C*B(3) "x, y, z: C[](3,1)= | |
(2)C[](3,3)=1,2,3,4,5,6,7,8,9 C[](3,3)= 1 2 3 4 5 6 7 8 9 DET(C)(3)=0 C[](3,3)=C+I C[](3,3)= 2 2 3 4 6 6 7 8 10 DET(C)(3)=-2 | |||
noscrivi=1 #j=0 label 0 #j=val(#j+1) i[2,#j]= ""out goto 0 if #j<5 " noscrivi=0 | (4) | ||
| (5) | |||
#k=0 for #i=1 to3: for #j=1 to 3: x[#k]=a[#i,#j]; #k=val(#k+1) x[](8)= | |||
| Un uso di RND per generare famiglie di figure con certe caratteristiche. Nell'esempio seguente vengono tracciati generici segmenti con estremi posti uno sull'asse x e l'altro sull'asse y in modo tale che la somma delle loro distanze dall'origine sia 1; ad es. se un estremo è (0, 0.8) l'altro è (0.2, 0) o (-0.2,0); il demo evidenzia la figura che questa famiglia di segmenti "descrive" (si tratta dell'inviluppo, ossia della curva che in ogni suo punto ha come tangente esattamente uno dei segmenti della famiglia). RND viene usato per prendere a caso la x dell'estremo sull'asse y (#x) e per prendere a caso la parte da cui cade l'altro (#s), oltre che per generare a caso il colore (#c). | |
noscrivi=1 nolista=1 tempo 0 n axes=2 scala sx:@0 sy:-1.5..1.5 #i=0 #c=int(rnd*5)+10 #s=sgn(rnd-.5) label 1 #x=val(rnd*2-1) plot x:s y:#c plot x:#x y:0 plot x:0 y:#s*(sgn(#x)*1-#x) #i=val(#i+1) stop goto 1 if #i<150 nolista=0 noscrivi=0 | 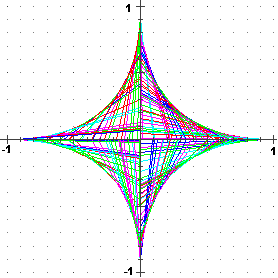 [con la versione a finestra quadrata si potrebbe usare il comando di scala: scala sx:-1.5..1.5 sy:-1.5..1.5: vedi] |
| L'assegnazione casuale mediante RND degli elementi di matrici per la generazione automatica di esercizi; a sinistra un demo, a destra un esempio d'esecuzione: | |
noscrivi=1 tempo=0 "Calcola AxB a mano e controlla il risultato #r=3;#c=4;#n=val(int(rnd*3)+1) "A a[](#r,#n)=rnd stamp=a[](#r,#n); " "B b[](#n,#c)=rnd stamp=b[](#n,#c); " "AxB c[](#r,#c)=a*b(#n) stamp=c[](#r,#c); " noscrivi=0 |
Calcola AxB a mano e controlla il risultato A 0 -6 6 6 -8 2 B 2 0 3 -6 8 3 -7 -1 AxB -48 -18 42 6 60 18 -24 -42 0 6 -38 46 |
| L'uso di varibili indiciate per calcoli con numeri complessi. Definiti x = x0+ix1 e y = y0+iy1 - qui: 3/2+2i e 7-(1+2/7)i - copiato il demo da noscrivi=1 a noscrivi=0 e comandato CLIP si ottengono x·y e x/y. "" serve per accumulare uscite da stampare in un'unica riga; out5 consente di ottenere la (eventuale) forma frazionaria. |
X[]=3/2,2 Y[]=7,-(1+2/7) noscrivi=1 tempo=0 "(x0 + i x1)*(y0 + i y1): X[0]*Y[0]-X[1]*Y[1]= ""out5 ""+ X[0]*Y[1]+X[1]*Y[0]= ""out5 "i "(x0 + i x1)/(y0 + i y1): (X[0]*Y[0]+X[1]*Y[1])/(y[0]^2+Y[1]^2)= ""out5 ""+ (-X[0]*Y[1]+X[1]*Y[0])/(Y[0]^2+Y[1]^2)= ""out5 "i noscrivi=0 (x0 + i x1)*(y0 + i y1): 183/14 + 169/14 i (x0 + i x1)/(y0 + i y1): 777/4964 + 1561/4964 i |
| Un esempio di uso di stamp=if …=0 acapo. Sotto il demo. A destra l'uscita. noscrivi=1 for #i=1 to 9:for #j=1 to 9:#p=val(#i*#j);stamp=#p;#k=val(#j-9);stamp=if K=0 acapo " noscrivi=0 | 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 3 6 9 12 15 18 21 24 27 4 8 12 16 20 24 28 32 36 5 10 15 20 25 30 35 40 45 6 12 18 24 30 36 42 48 54 7 14 21 28 35 42 49 56 63 8 16 24 32 40 48 56 64 72 9 18 27 36 45 54 63 72 81 |
| L'uso di SUBV (e di #cbin e #theta) per calcolare valori di funzioni di più variabili (una probabilità di tipo binomiale e la direzione in gradi di un vettore): | |
#C=#CBIN*#P^#K*(1-#P)^(#N-#K) SUBV(#P=0.5,#N=20,#K=7,#C) 0.07392883300781251 =4845/65536 | #D=#theta/GR SUBV(#X=3,#Y=-3,#D) 315 |
| Il tracciamento (mediante un clclo for), dopo quello del grafico di una gaussiana F di media 0 e s.q.m. 1, della sua funzione di ripartizione, costruita come funzione integrale con grafico passante per (0,0) (la funzione che a x associa | 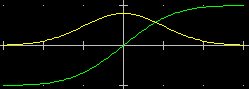 |
#m=0; #s=1; f(x)=gauss #a=-3;#b=3 plot x:#a..#b y:f | 14 #h=val((#b-#a)/101) plot x:s y:10 for #i=0 to 101: #x=#a+#i*#h; #y=[0,#x] f int; plot x:#x y:#y | |
Il grafico (tra -2π e 2π) della "funzione integrale passante per (-2,2)" della stessa funzione F di cui sopra ho tracciato il grafico di un'altra funzione integrale con "plot y=INTEGR" (x  Ho usato INTD invece di INT in quanto F è una funzione non continua nell'intervallo ("int" usa delle interpolazioni che possono dar luogo a valutazioni errate in presenza di punti di discontinuità). | 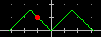 |
F(X)=SGN(SIN(x)) plot x:s y:10 #N=51; #H=4*PI/#N FOR #I=0 TO #N: #X=VAL(-2PI+#H*#I); #Y=[-2,#X] F INTD; PLOT x:#X y:#Y+2 | |
| L'uso di SUM può essere utile anche per studiare serie di funzioni.
Ecco un demo per tracciare i grafici per diversi N (1, 2, …, 10; i codici-colore, scelti pari a N+5, consentono di associare le varie curve al corrispondente N:
vedi figura sotto a sinistra) di x-x^3/6+x^5/120 … |
F(X)=(-1)^(x+1)*#x^(2x-1)/!(2x-1) tempo=0 noscrivi=1 nolista=1 scala sx:-1..3*pi sy:-3..3 scrivi -0.5,-1:Pol. Taylor 1°, 3°.. 19° di sin #n=1 #a=0;#b=3*pi;#h=(#b-#a)/51 label 1 stop plot x:s y:#n+5 for #i=0 to 51: #x=#a+#i*#h; #y=[1,#n] f sum; plot x:#x y:#y #n=val(#n+1) goto 1 if #n<11 nolista=0 noscrivi=0 |
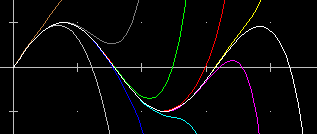  | 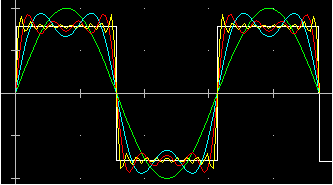 |
| Sopra a destra c'è quanto si ottiene per la somma trigonometrica sin(x)+sin(3x)/3+ … sin((2N+1)x)/(2N+1), per diversi valori di N, col demo seguente (in bianco è tracciato il grafico della funzione limite). |
F(x)=sin(#x*(2x+1))/(2x+1) tempo=0 noscrivi=1 nolista=1 scala sx:-1..3*pi sy:-2..2 #a=0;#b=3*pi;#h=val((#b-#a)/101) plot x:s y:10 for #i=0 to 101: #x=#a+#i*#h; #y=[0,0] f sum; plot x:#x y:#y plot x:s y:11 for #i=0 to 101: #x=#a+#i*#h; #y=[0,1] f sum; plot x:#x y:#y plot x:s y:12 for #i=0 to 101: #x=#a+#i*#h; #y=[0,3] f sum; plot x:#x y:#y plot x:s y:14 for #i=0 to 101: #x=#a+#i*#h; #y=[0,9] f sum; plot x:#x y:#y noscrivi=0 nolista=0
|
Sotto il demo per generare le curve di livello di una funzione di 2 variabili a diverse quote, rappresentate, in ordine, coi colori 8, …, 14. Più sotto una alternativa, con un demo d'uso più generale. Più sotto ancora come tracciarne il grafico in prospettiva parallela direttamente con Poligon (figura a sinistra) e un demo per generare il file che lo rappresenta in formato TreDim (nella figura sotto a sinistra una delle possibili visioni prospettiche del grafico realizzabili con TreDim): le coordinate per Tredim vengono memorizzate con i comandi stamp" e "clip; la figura può essere richiamata in TreDim col comando CLIP. |
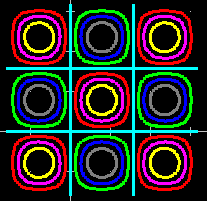  |
F(x,y)=sin(x)*sin(y)
z[]=-0.75,-0.5,-0.25,0,0.25,0.5,0.75
noscrivi=1
punt=1
for #i=0 to 6: plot x:f(x,y)=z[#i] | 8+#i n=80 y:-pi..2pi|-pi..2pi
noscrivi=0
Alternativa:
F(x,y)=sin(x)*sin(y)
#n=7
z[]=-0.75,-0.5,-0.25,0,0.25,0.5,0.75
x[]=-pi,pi
y[]=-pi,pi
--------------
noscrivi=1
tempo=0
u[]=15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,15,14,13,12,11
legenda=1
plot x:x[0]..x[1] y:y[0]..y[1]
scala sx:x[0]..x[1] sy:y[0]..y[1]
-
punt=1
for #i=1 to #n: plot x:f(x,y)=z[#i-1] | u[#i-1] y:x[0]..x[1]|y[0]..y[1]
noscrivi=0
| |
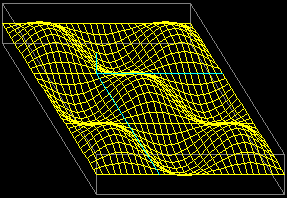 | 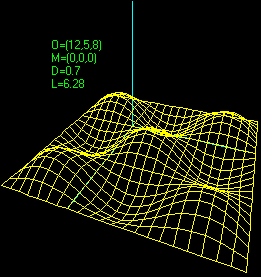 |
|
F(x,y)=sin(x)*sin(y) X[]=2PI,0,0,0,0 Y[]=0,0,2PI,0,0 Z[]=0,0,0,0,1 3db(f+4,-pi,2pi,-pi,2pi, -1,1, 30, 30, -1/2,0.8) | |
|
noscrivi=1 nolista=1 tempo 0 cifre=3 #Z=sin(#x)*sin(#y) #A=-pi; #B=2pi; #C=-pi; #D=2pi; #n=21 #i=-1 "clip label 0 #i=val(#i+1) #H=val((#B-#A)/#N); #k=val((#d-#c)/#N) FOR #J=0 TO #n: #X=#A+#h*#I; #Y=#C+#k*#J;stamp=#x#y#z stamp=s; stamp=acapo goto 0 if #i<#n #J=-1 label 1 #j=val(#j+1) FOR #I=0 TO #n: #X=#A+#h*#I; #Y=#C+#k*#J;stamp=#x#y#z stamp=s; stamp=acapo goto 1 if #j<#n "CLIP cifre=7 nolista=0 noscrivi=0 | |
| Per sezionare grafici o restringere domini possiamo ricorrere alle "funzioni" >, <, .... Ecco un esempio: come vedere la parte sopra al piano z=0 del grafico z=f(x,y) precedente [il trucco è mettere la divisione per qualcosa che valga 1 quando vogliamo che il grafico sia tracciato e valga 0 altrimenti). Nota: invece di f(x,y)≥0 si è messo f(x,y)-0.000001>0 (che equivale a f(x,y)>-0.000001) per tener conto che per problemi di arrotondamento il programma potrebbe "perdere" dei punti in cui f(x,y)=0. | 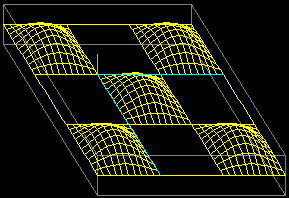 |
|
G(x,y)=sin(x)*sin(y) / ((sin(x)*sin(y)+1e-6)>0) X[]=2PI,0,0,0,0 Y[]=0,0,2PI,0,0 Z[]=0,0,0,0,1 3db(G+4,-pi,2pi,-pi,2pi, -1,1, 30, 30, -1/2,0.8) | |
| Volendo, con un doppio click su [P], si possono unire grafici fatti in colori diversi, purché con lo stesso punto di vista. Ecco un esempio riferito sempre alla stessa funzione considerata sopra. | 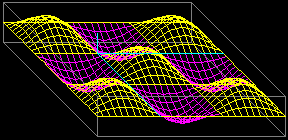 |
|
X[]=2PI,0,0,0,0 Y[]=0,0,2PI,0,0 Z[]=0,0,0,0,1 G(x,y)=sin(x)*sin(y) / ((sin(x)*sin(y)-1e-6)<0) 3db | 13(G+4,-pi,2pi,-pi,2pi, -1,1, 30, 30, -1/2,0.5) G(x,y)=sin(x)*sin(y) / ((sin(x)*sin(y)+1e-6)>0) 3db | 14(G+4,-pi,2pi,-pi,2pi, -1,1, 30, 30, -1/2,0.5) pp |
| Un altro esempio di generazione di una figura per TreDim. La figura è qui sotto rappresentata da diversi punti di vista. |
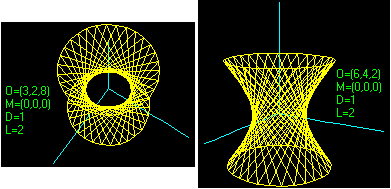 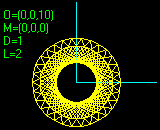 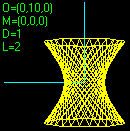 |
noscrivi=1 nolista=1 tempo 0 cifre=3 #x=cos(#t) #y=sin(#t) #a=cos(#t+2pi/3) #b=sin(#t+2pi/3) #z=1 #c=-1 #n=30 #H=val(2pi/#n) FOR #i=0 TO #n: #t=#h*#i;stamp=#x#y#z;stamp=#a#b#c;stamp=s;stamp=acapo FOR #i=0 TO #n: #t=#h*#i;stamp=#x#y#c;stamp=#a#b#z;stamp=s;stamp=acapo FOR #i=0 TO #n: #t=#h*#i;stamp=#x#y#c stamp=acapo FOR #i=0 TO #n: #t=#h*#i;stamp=#a#b#z "CLIP cifre=7 nolista=0 noscrivi=0 |
| La definizione di una matrice A, la definizione del suo polinomio caratteristico, di cui poi (vedi figura a lato) si può tracciare il grafico, che è di aiuto per l'impostazione del calcolo degli autovalori. | 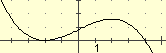 |
|
A[](3,3)=1,-3,3,3,-5,3,6,-6,4 A[](3,3)= 1 -3 3 3 -5 3 6 -6 4 F(x) = (A[1,1]-x)*((A[2,2]-x)*(A[3,3]-x)-A[3,2]*A[2,3]) - A[1,2]*(A[2,1]*(A[3,3]-x)-A[3,1]*A[2,3]) + A[1,3]*(A[2,1]*A[3,2]-A[3,1]*(A[2,2]-x)) | |
| Il calcolo dell'autovalore positivo e di quello negativo, che ha molteplictà 2, e che viene determinato attraverso una ricerca di un minimo (c'è anche la verifica che per l'approssimazione -2 del valore ottenuto si abbia F(-2)=0). Segue, sempre come esempio, la verifica che per l'autovalore λ = -2 si abbia effettivamente det(A-λI) = 0. | |
|
[0,8] F(X)=0 se x= 4 [-8,0] F MIN se x= -2.00000000158156 -2 y=7.503987302457E-18 F(-2)=0 #L=-2 B[](3,3)=#L*I B[](3,3)=A-B DET(B)(3)=0 | |
| Una trasformazione affine o proitettiva può essere realizzata anche interpretando i punti come vettori colonna (x,y,1) e moltiplicando una opportuna matrice A 3×3; per ciascuono di questi. Se A per il vettore (x,y,1) fornisce il vettore colonna (a,b,c) si prende (x',y',1) = (a/c,b/c,c/c). | |||||
|
Ecco un demo che trasforma un esagono regolare secondo la matrice A che l'utente deve aver definito in precedenza. Ecco (in ordine) quanto si ottiene per le seguenti matrici (assegnate con | 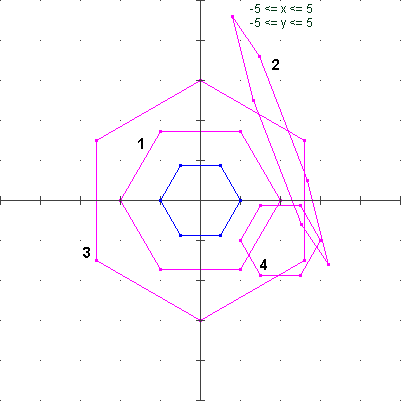 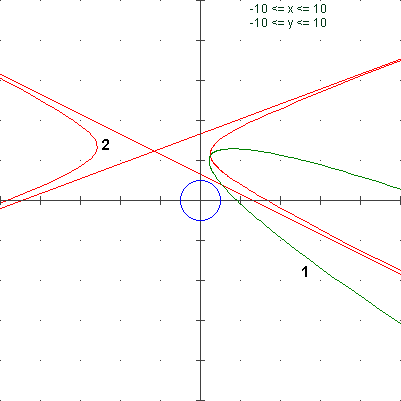 | ||||
2 0 0 2/3 -1 2 0 1 0 1 0 2 0 2 0 -1 3 3/2 1 0 0 0 1 -1 0 0 1 0 0 1 0 0 1/3 0 0 1 | |||||
a[](3,3)= noscrivi=1 nolista=1 legenda=1 tempo=0 color 14 p6 numpunti plot x:s y:10 #N=val(%) #i=0 label 0 #i=val(#i+1) punto(#i) B[](3,1)=%1,%,1 C[](3,1)=A*B(3) plot x:C[1,1]/C[3,1] y:C[2,1]/C[3,1] goto 0 if #i<#n nolista=0 noscrivi=0 | |||||
| Ecco, a destra, in ordine, che cosa si ottiene (una parabola e un'iperbole) trasformando un cerchio invece di un esagono (ossia mettendo c invece di p6) e definendo la matrice A nei modi seguenti. | |||||
2/3 -1 2 2/3 -1 2 1 3 3/2 2 1 3 0 1 1 1 1 1 | |||||
| Avremmo potuto più semplicemente e con un'esecuzione più veloce, tracciata una qualunque figura, azionare (senza ricorre a un ciclo GO-TO) l'unico comando PLOT seguente, in cui abbiamo già sviluppato il calcolo del trasformato di (x,y): | |||||
| |||||