Sotto sono rappresentati i dati relativi allo studio di una macchina semplice, che trasforma una certa forza di intensità x (kg) in una forza minore, di intensità y (kg). I valori di x sono 10, 17, 30, 47 con le precisioni 1, 1, 1, 1.5. I valori di y sono 4.4, 6.9, 11.6, 18.9 tutto con la precisione 0.2 Sapendo che le due forze x e y sono direttamente proporzionali, ricava un intervallo di indeterminazione per il coefficiente di proporzionalità.
    Below are the data relating to the study of a simple machine, which transforms a certain force of intensity x (kg) into a minor force of intensity y (kg). The values of x are 10, 17, 30, 47 with the precisions 1, 1, 1, 1.5. The values of y are 4.4, 6.9, 11.6, 18.9 all with precision 0.2 Knowing that the two forces x and y are directly proportional, obtain an uncertainty interval (an interval arithmetic) for the proportionality coefficient.


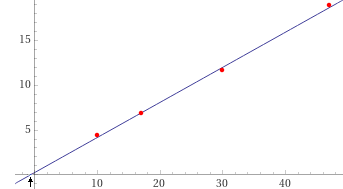
Un procedimento decisamente sbagliato, che non tiene conto che la retta deve passare per (0,0):
A decidedly wrong procedure, which does not take into account that the line must pass through (0,0):



    Ecco come si può procedere.
In tre esperimenti ottengo le coppie (G1,G2) rappresentate a lato con i punti A, B e C.  Cerco, tra tutti i grafici del tipo G2 = k G1, quello che rende minima la somma dei quadrati degli scarti tra i valori di G2 sperimentali e quelli che sarebbero stati associati ai valori G1 dalla relazione G2 = k G1. Ossia cerco la pendenza k che deve avere una retta passante per l'origine affinché la somma dei quadrati di a, b e c (vedi fig. a lato) sia minima.
  a = |yA - k xA|, b = |yB - k xB|, c = |yC - k xC|.
  a²+ b²+ c² = (k xA - yA)²+ (k xB - yB)²+ (k xC - yC)².
È un'espressione polinomiale in k di secondo grado. Assume valore minimo quando si annulla la sua derivata rispetto a k, ossia quando:
  2(k xA - yA)xA + 2(k xB - yB)xB + 2(k xC - yC)xC = 0   ossia:
  k = (xAyA+ xByB+ xCyC)/(xA² + xB² + xC²).
Se avessi imposto che la retta passasse per (p,q) invece che per O avrei potuto effettuare un calcolo analogo ottenendo:
  k = ( (xA-p)(yA-q)+(xB-p)(yB-q)+(xC-p)(yC-q) ) / ( (xA-p)² +(xB-p)² + (xC-p)² ). 		  
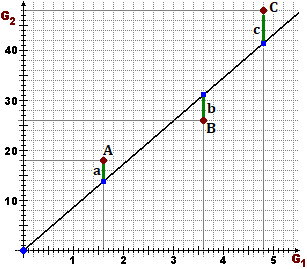
    Here's how you can go about it.  In three experiments I obtain the pairs (G1,G2) represented on the side with the points A, B and C. I search, among all the graphs of the type G2 = k G1, the one that minimizes the sum of the squares of the differences between the experimental G2 values and those that would have been associated with G1 values by the relation G2 = k G1. That is, I look for the slope k which must have a straight line passing through the origin so that the sum of the squares of a, b and c is minimum.
 a = |yA - k xA|, b = |yB - k xB|, c = |yC - k xC|    a²+ b²+ c² = (k xA - yA)²+ (k xB - yB)²+ (k xC - yC)².
It is a polynomial expression in k of the second degree. It has a minimum value when its derivative with respect to k is canceled, that is when:
  2(k xA - yA)xA + 2(k xB - yB)xB + 2(k xC - yC)xC = 0  i.e.  k = (xAyA+ xByB+ xCyC)/(xA² + xB² + xC²).
If I had imposed that the line passed through (p,q) instead of O, I could have performed a similar calculation obtaining:
  k = ( (xA-p)(yA-q)+(xB-p)(yB-q)+(xC-p)(yC-q) ) / ( (xA-p)² +(xB-p)² + (xC-p)² ).


Torniamo al problema iniziale  /  Let's go back to the initial problem

( 10*4.4+17*6.9+30*11.6+47*18.9 ) / ( 10^2+17^2+30^2+47^2 )
 0.3995425957...
y = 0.3995 x
Ma potrei usare un semplice script / But I could use a simple script  (vedi/see)


Per fare il grafico con "linear fit" posso aggiungere un po' di punti fissi / To make the graph with "linear fit" I can add some fixed points

{(10,4.4),(17,6.9),(30,11.6),(47,18.9), (0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0),(0,0)}



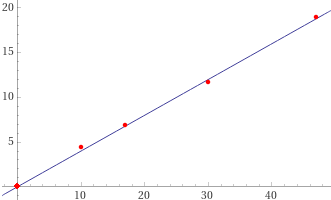
Ma anche procedendo così non ho tenuto conto delle precisioni / But even proceeding in this way, I did not take into account the uncertainties
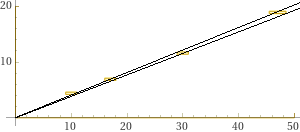
La corretta soluzione, trovata graficamente / The correct solution, found graphically


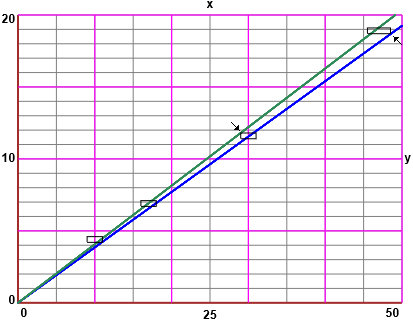
La retta di minima pendenza passa per (47+1.5,18.9-0.2); 18.7/48.5 = 0.38556…  Quella di massima pendenza per (30-1,11.6+0.2); 11.8/29 = 0.40689…
The line of minimum slope passes through (47+1.5,18.9-0.2); 18.7/48.5 = 0.38556…  That of maximum slope through (30-1,11.6+0.2); 11.8/29 = 0.40689…

Come potremmo fare il grafico con / How could we chart with  WolframAlpha:
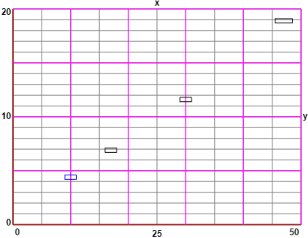
rectangle (0,0),(50,0),(50,20),(0,20), rectangle (47-1.5,18.9-0.2),(47-1.5,18.9+0.2),(47+1.5,18.9+0.2),(47+1.5,18.9-0.2)



Abbiamo tracciato un punto, con l'immagine che può essere (ingrandita e poi) copiata in Paint o in un'altra applicazione grafica.
We have drawn a point, with the image that can be (enlarged and then) copied into Paint or another graphics application.



Posso colorare bianca la base del grafico, tracciare i grafici degli altri punti e incollarli in trasparenza sul primo grafico.
I can paint the base of the graph white, draw the graphs of the other points and paste them transparently on the first graph.

rectangle (0,0),(50,0),(50,20),(0,20), rectangle (30-1,11.6-0.2),(30-1,11.6+0.2),(30+1,11.6+0.2),(30+1,11.6-0.2)
rectangle (0,0),(50,0),(50,20),(0,20), rectangle (17-1,6.9-0.2),(17-1,6.9+0.2),(17+1,6.9+0.2),(17+1,6.9-0.2)
rectangle (0,0),(50,0),(50,20),(0,20), rectangle (10-1,4.4-0.2),(10-1,4.4+0.2),(10+1,4.4+0.2),(10+1,4.4-0.2)


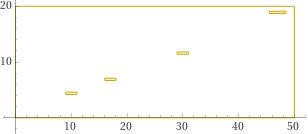
Poi posso colorare di bianco il bordo e trovare graficamente le rette di minima e massima pendenza.
Then I can color the edge white and graphically find the lines of minimum and maximum slope.


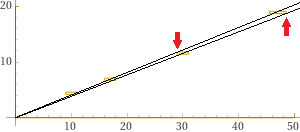
Senza utilizzare il grafico potremmo fare i calcoli con / Without using the graph we could do the calculations with  WolframAlpha:
max {(4.4-0.2)/(10+1), (6.9-0.2)/(17+1), (11.6-0.2)/(30+1), (18.9-0.2)/(47+1.5)}
0.385567
min {(4.4+0.2)/(10-1), (6.9+0.2)/(17-1), (11.6+0.2)/(30-1), (18.9+0.2)/(47-1.5)}
0.406897
Posso dedurre che y/x varia tra 0.38 e 0.41 / I can deduce that y/x varies between 0.38 and 0.41

La retta di minima pendenza passa per (47+1.5,18.9-0.2); 18.7/48.5 = 0.38556… ≥ 0.38. Quella di massima pendenza per (30-1,11.6+0.2); 11.8/29 = 0.40689… ≤ 0.41.
La retta di minima pendenza passa per (47+1.5,18.9-0.2); 18.7/48.5 = 0.38556… ≥ 0.38. Quella di massima pendenza per (30-1,11.6+0.2); 11.8/29 = 0.40689… ≤ 0.41.
Senza utilizzare il grafico potremmo fare i calcoli con WolframAlpha:
max {(4.4-0.2)/(10+1), (6.9-0.2)/(17+1), (11.6-0.2)/(30+1), (18.9-0.2)/(47+1.5)}
  0.385567
min {(4.4+0.2)/(10-1), (6.9+0.2)/(17-1), (11.6+0.2)/(30-1), (18.9+0.2)/(47-1.5)}
  0.406897

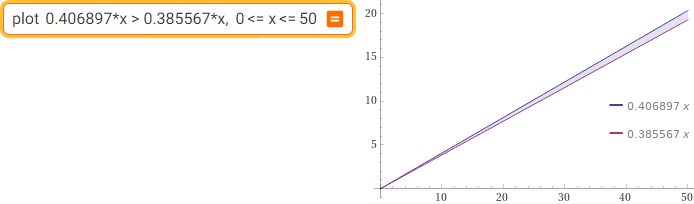
plot 0.406897*x > 0.385567*x, 0 <= x <= 50
Posso dedurre che y/x varia tra 0.38 e 0.41 / I can deduce that y/x varies between 0.38 and 0.41

Se volessi potrei tracciare le rette sulla stessa scala e sovrapporre ad esse il grafico precedente
If I wanted to, I could draw the lines on the same scale and superimpose the previous graph on them
rectangle (0,0),(50,0),(50,20),(0,20), rectangle (0,0),(50,50*0.406897),(50,50*0.406897),(0,0), rectangle (0,0),(50,50*0.385567),(50,50*0.385567),(0,0)

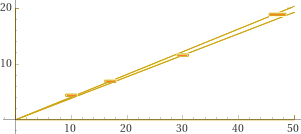
Qui/here il grafico in JavaScript