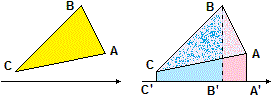Area

  In Fisica e nella pratica per ottenere una misura approssimata per difetto di una lunghezza si conta quante volte si possono riportare (senza superare tale lunghezza) degli oggetti dalla forma di segmento assunti come unità, ad esempio il metro e :  il centimetro, ottenuto suddividendo il metro in 100 segmenti uguali, il chilometro, ottenuto congiungendo 1000 metri, ….  Analogamente, per ottenere un'approssimazione per difetto dell'area di una superficie, nei casi più semplici si può contare quante copie di oggetti di forma quadrata si possono inserire, senza sovrapposizioni, in tale superficie.
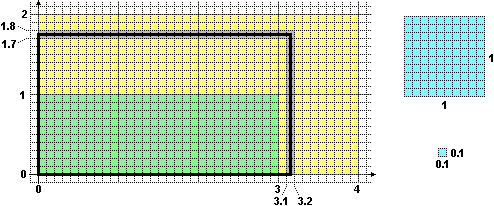
    Ad esempio nel caso della superficie rettangolare riprodotta sotto a sinistra, avente i lati lunghi 3.1… cm e 1.7… cm, posso inserire 3 quadrati di lato 1 cm. Se chiamo cm² uno di questi quadrati, posso dire che 3 cm² è un'approssimazione per difetto dell'area del rettangolo considerato.
    Ma posso inserirvi anche 31 per 17 quadrati di lato 1 mm, ossia prendere 527 mm² come approssimazione per difetto dell'area del rettangolo considerato. Poiché in 1 cm² contiene esattamente 100 mm² e 527/100 = 5.27, posso esprimere questa misura anche come 5.27 cm², valore che potevo ottenere direttamente moltiplicando le approssimazioni per difetto ai centimetri (3.1 e 1.7) dei lati del rettangolo.

    In Matematica, dove possiamo supporre di conoscere "esattamente", cioè con tutte le cifre che vogliamo, le lunghezze dei due lati, possiamo definire come area del rettangolo il prodotto di tali lunghezze: man mano che calcoliamo questo prodotto usando approssimazioni di queste con più cifre otteniamo come risultato una approssimazione via via migliore dell'area.
    Del resto l'estensione delle operazioni tra numeri interi ad operazioni tra numeri reali si basa proprio sull'idea di trovare modelli matematici per alcune attività di tipo fisico: per sommare lunghezze nel caso dell'addizione e per valutare l'estensione di una superficie rettangolare nel caso della moltiplicazione. Abbiamo usato questa idea anche per illustrare questioni di calcolo approssimato e per motivare alcune proprietà algebriche.
    Nel caso di un rettangolo avente lati lunghi 3.1… e 1.7… (in matematica le lunghezze sono numeri, senza unità di misura), possiamo quantificare via via anche la precisione delle misure: l'area è compresa tra 3·1= 3 e 4·2= 8, anzi tra 3.1·1.7= 5.27 e 3.2·1.8= 5.76, anzi …

Più in generale, l'area di una qualunque figura del piano cartesiano può essere definita come il numero che si ottiene attraverso approssimazioni successive nel modo seguente:
• suddivido il piano in quadrati di lato 1 (quelli che hanno vertici nei punti (m,n) con m, n numeri interi) e conto quanti sono contenuti nella figura, • poi suddivido questi quadrati in 100 quadratini, ossia suddivido il piano in quadrati di lato 0.1, calcolo quanti sono quelli contenuti in essa e divido questo numero per 100 (in quanto 1 quadrato di lato 1 contiene 100 quadrati di lato 0.1), • poi suddivido il piano in quadrati di lato 0.01, calcolo quanti ne contiene la figura e divido per 10000, ….     Ad es. il triangolo a lato contiene 9+8+7+6+5+4+3+2+1 = (9+1)+(8+2)+(7+3)+(6+4)+5 = 45 quadrati di lato 0.1; approssimo la sua area con 0.45.  La parte non ancora coperta da questi quadretti è costituita da 10 triangoli della stessa forma, ciascuno dei quali (come si vede con la "lente") contiene a sua volta 9+8+7+6+5+4+3+2+1 = 45 quadrati di lato 0.01; quindi a 0.45 aggiungo 0.045, ottenendo 0.495.
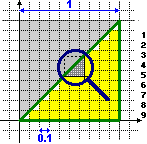Procedendo in modo simile aggiungo 0.0045, ottenendo 0.4995, poi aggiungo 0.00045 ottenendo 0.49995, …, ossia ottengo una successione di numeri che tende a stabilizzarsi su 0.4999…, ossia [] su 0.5. Questa è l'area del triangolo.

Potevo arrivare a questa conclusione anche in un modo differente: il nostro triangolo deve avere area pari a metà dell'area del quadrato avente lato 1 costituito dall'unione del triangolo stesso e di quello ottenuto con un suo ribaltamento attorno al lato più lungo. Infatti i due triangoli sono uguali. L'area del quadrato è 1·1 = 1, quindi l'area del triangolo è 1/2 = 0.5.
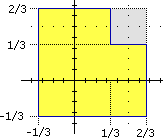	Anche nel caso della figura a lato invece che procedere contando quanti quadrati di lato 1, quanti di lato 0.1, … contiene possiamo ragionare in modo diverso:     se alla figura attacchiamo un quadrato di lato 1/3 (e area 1/9) otteniamo un quadrato di lato 1 (e area 1); quindi la sua area sommata a 1/9 deve dare 1, ossia deve essere 8/9.     Nel primo caso abbiamo implcitamente usato il fatto che figure isometriche hanno la stessa area. È una cosa intuitiva: se con traslazioni, rotazioni e ribaltamenti posso trasformare una figura in un'altra le due figure sono "sovrapponibili" e quindi di uguale estensione.
Comunque nel caso dei due triangoli considerati l'uguaglianza delle loro aree è anche verificabile utilizzando la definizione di area data sopra: i due triangoli contengono esattamente le stesse quantità di quadrati di lato 0.1, di quadrati di lato 0.01, di quadrati di lato 0.001, …. La cosa può essere domostrata in generale.     In entrambi i casi abbiamo poi usato il fatto che se unisco delle figure [X1, X2, X3, …] che non hanno punti in comune o hanno in comune figure di area 0 (come un segmento, che ha area 0 poiché non contiene quadretti di lato 0.1, né di lato 0.01, …, ovvero poiché può essere pensato come un rettangolo che ha un lato lungo 0) ottengo una figura che ha come area la somma delle aree delle figure [Area(X1)+Area(X2)+Area(X3)+…].     Anche questa proprietà, che viene chiamata proprietà additiva, è intuitiva ma potrebbe essere dimostrata a partire dalla nostra definizione.

  L'area dei parallelogrammi

Consideriamo un parallelogramma (quadrangolo con lati a due a due paralleli) come composto da tante striscioline disposte parallelamente a uno dei lati, ad es. come se fosse realizzato con tante cannucce da bibita. Se facciamo scorrere le striscioline in modo che le loro estremità rimangano allineate, nel corso del movimento il parallelogramma cambia forma ma mantiene (per la proprietà additiva) la stessa area (la somma delle aree di tutte le striscioline).     Indichiamo con l la lunghezza del lato che rimane fisso e con h la distanza tra la retta a cui esso appartiene e il lato opposto. Durante il movimento h non varia.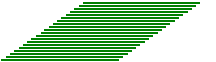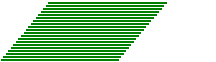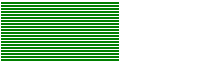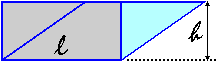

Possiamo, in particolare, trasformare (senza mutare l'area) il nostro paralleogramma in un rettangolo avente l e h come dimensioni.     AreaParallelogramma = AreaRettangolo = l · h     Nell'immagine soprastante il parallelogramma è diposto come se fosse appoggiato sul lato scelto. Se il parallelogramma fosse disposto diversamente potrei comunque posizionarmi (o ruotare il piano) in modo da vederlo appoggiato su tale lato, così da poter pensare l come "base" e h come "altezza" del parallelogramma. Con questa convenzione la formula precedente può essere riscritta come:     AreaParallelogramma = Base · Altezza     o:     AreaParallelogramma = Lato · AltezzaRelativa dove con altezza relativa a un lato si intende la distanza tra retta a cui appartiene e il lato opposto ( distanza tra figure)

Nota. Se realizzo concretamente la trasformazione descritta sopra mi convinco senza alcuna ombra di dubbio che parallelogrammi di uguale "base" e uguale "altezza" hanno la stessa estensione, ossia che sono costruibili con lo stesso insieme di striscioline. Cerchiamo, tuttavia, di capire con qualche ragionamento "matematico", senza ricorrere a una prova "fisica", perché spostando le striscioline riesco a riottenere un parallelogramma.
Per trovare questa spiegazione posso riferirmi a un altro fenomeno: se con la luce del sole (che posso pensare costituita da tanti raggi paralleli) proietto su un muro una immagine disegnata su un vetro tenuto parallelo al muro, l'immagine viene riprodotta nelle stesse dimensioni, indipendentemente dalla distanza del vetro dal muro.     Analogamente nel caso del parallelogramma iniziale ho che tutte le striscioline sono lunghe tanto quanto la base, e sono uguali in tutti i parallelogrammi di eguale base.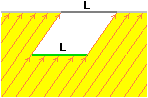
La spiegazione "matematica" è semplice: se pensiamo il parallelogramma con la base sull'asse y, i due lati non paralleli ad essa stanno su rette che hanno la stessa pendenza: poiché, se vario x, sulle due rette y subisce la stessa variazione, ogni segmento verticale ottenuto sezionando il parallelogramma ha la stessa lunghezza L della "base" (vedi figura a lato); infatti la y dei due estremi è aumentata della stessa quantità e quindi la loro distanza non è cambiata.

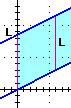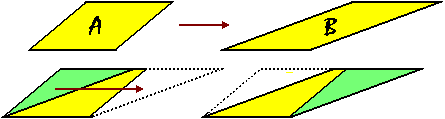
  Si può dimostrare che paralleogrammi con uguale base e uguale altezza hanno uguale area anche in un altro modo. Consideriamo prima due paralleogrammi come i seguenti A e B: con la traslazione di un triangolo posso trasformazione A in B: le due figure sono composte dalle stesse parti, per cui, per la proprietà additiva, hanno la stessa area.

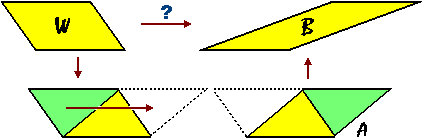
    Nel caso dei parallelogrammi W e B seguenti non posso procedere con una sola traslazione di un triangolo in quanto hanno l'inclinazione dei lati non orizzontali è molto diversa. Mediante un numero finito di traslazioni simili alla W A sotto illustrata posso comunque ricondurmi al caso precedente:

  L'area dei triangoli

Consideriamo un triangolo come composto da tante striscioline disposte parallelamente a uno dei tre lati, ad es. come se fosse realizzato con tante cannucce da bibita. Se facciamo scorrere le striscioline in modo che le loro estremità rimangano allineate, nel corso del movimento il triangolo cambia forma ma mantiene la stessa area (la somma delle aree di tutte le striscioline).     Indichiamo con l la lunghezza del lato che rimane fisso e con h la distanza tra la retta a cui esso appartiene e il vertice opposto. Durante il movimento h non varia.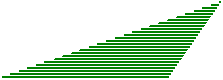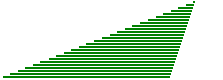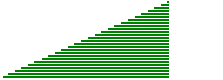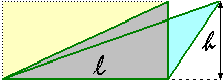

Possiamo, in particolare, trasformare (senza mutare l'area) il nostro triangolo nel triangolo rettangolo pari a metà del rettangolo avente l e h come dimensioni.     AreaTriangolo = AreaRettangolo / 2 = l · h / 2     Nell'immagine soprastante il triangolo è diposto come se fosse appoggiato sul lato scelto. Se il triangolo fosse disposto diversamente potrei comunque posizionarmi (o ruotare il piano) in modo da vederlo appoggiato su tale lato, così da poter pensare l come "base" e h come "altezza" del triangolo. Con questa convenzione la formula precedente può essere riscritta come:     AreaTriangolo = Base · Altezza / 2     o:     AreaTriangolo = Lato · AltezzaRelativa / 2 dove con altezza relativa a un lato si intende la distanza tra la retta a cui esso appartiene e il vertice opposto ( distanza tra figure)

Nota. Se realizzo concretamente la trasformazione descritta sopra mi convinco senza alcuna ombra di dubbio che i triangoli di uguale "base" e uguale "altezza" hanno la stessa estensione, ossia che sono costruibili con lo stesso insieme di striscioline. Cerchiamo, tuttavia, di capire con qualche ragionamento "matematico", senza ricorrere a una prova "fisica", perché spostando le striscioline riesco a riottenere un triangolo.
Per trovare questa spiegazione posso riferirmi a un altro fenomeno: se proietto su un muro una immagine disegnata su un vetro tenuto parallelo al muro, l'immagine viene ingrandita di un fattore che è pari al rapporto tra la distanza della lampadina dal piano del muro e la distanza della lampadina dal piano del vetro. Nel caso raffigurato a lato d2/d1 = 1.5, per cui la scala di ingrandimento è 1.5.     Tutte le immagini sul vetro sono ingrandite con la stessa scala, così come accade per le parti di una diapositiva [o di un fotogramma di una pellicola cinematografica]: che siano vicine o siano lontane dal centro della diapositiva (se questa è parallela allo schermo), sono ingrandite allo stesso modo, senza che la fotografia venga deformata. E se due immagini proiettate sono grandi uguali, devono essere uguali le immagini originali di cui sono la riproduzione.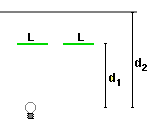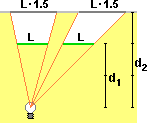
Analogamente nel caso del triangolo iniziale ho che la lunghezza di una strisciolina dipende solo da quanto la retta su cui essa sta dista dal vertice, non dalla inclinazione del triangolo.     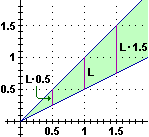La spiegazione "matematica" è semplice: se pensiamo il vertice del triangolo collocato in (0,0) e il lato ad esso opposto disposto parallelamente all'asse y, gli altri due lati stanno su rette che rappresentano una relazione di porporzionalità tra x e y: poiché y varia proporzionalmente a x, se, dato il segmento L (vedi figura a lato), considero il segmento che ha distanza dall'asse verticale dimezzata (ossia se dimezzo x), anche la lunghezza di questo è metà (in quanto le y degli estremi sono dimezzate); se moltiplico per 1.5 la distanza dall'asse verticale ottengo un segmento che ha lunghezza moltiplicata per 1.5; ….

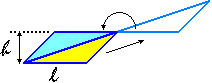
Si può ottenere lo stesso risultato osservando che l'unione a un triangolo di un triangolo ad esso uguale (realizzata nel modo illustrato a lato, con una traslazione e una rotazione di 180°) dà luogo a un parallelogramma. Dunque l'area del triangolo è uguale a metà della area del parallelogramma così ottenuto, ossia:
AreaTriangolo = l · h / 2

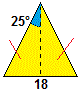Ovviamente, usando le funzioni circolari, si può ricavare l'area di un triangolo anche utilizzando altre informazioni.  Ad esempio se del triangolo raffigurato a lato conosco le misure indicate, posso ottenerne l'area nel seguente modo: indicata con h l'altezza, so che 9/h = tan(25°), da cui h = 9/tan(25°) e, quindi, l'area è 18·9/tan(25°)/2 = 81/tan(25°), che se voglio calcolo (col computer o con la calcolatrice): 81/tan(25·π/180) = 173.7051 (valore arrotondato).     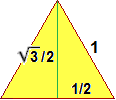Nel caso di un triangolo equilatero posso procedere analogamente oppure direttamente, utilizzando il teorema di Pitagora:  se il lato è lungo 1, l'altezza è √(1−(1/2)²) = √(3/4) = √3/2.  Quindi l'area è √3/2·1/2 = √3/4 = 0 . 4330127…  Come vedremo meglio fra poco () nel caso in cui il triangolo abbia lato L l'area è √3/4·L².

    La forma di un triangolo, a differenza di quella dei quadrangoli, dipende solo dalla lunghezza dei suoi lati.  Quindi è possibile determinare l'area di un triangolo solo a partire da dalla lunghezza dei suoi lati. In moltissime situazioni procedere in questo modo è molto più semplice che usare la formula "base·altezza/2".  Di questo di discute più avanti.

  L'area dei cerchi

Per determinare l'area del cerchio x2+ y2 = 1 (o meglio, x2+ y2 ≤ 1, dato che ci riferiamo anche ai punti interni) possiamo procedere sia direttamente approssimandola con unioni di quadretti, sia utilizzando opportunamente la proprietà additiva.     Il primo metodo è illustrato nella figura a lato nel caso dei quadretti di lato 0.1 e per un quarto di cerchio; per gli altri tre quarti la situazione è analoga. Vi sono 67·4 = 268 quadretti contenuti, per cui 2.68 è una approssimazione per difetto; contando anche i quadretti a cavallo del bordo otteniamo 86·4 = 344 quadretti, per cui 3.44 è una approssimazione per eccesso.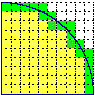
Sotto è riportato che cosa si otterrebbe suddividendo ulteriormente i quadretti:
Lato quadretto <= Area <= 0.1 2.68 3.44 0.01 3.1016 3.1796

I valori precedenti sono stati ottenuti col seguente programma, redatto in R, nel quale per contare i quadretti contenuti si è valutato per ciascuno di essi se il vertice più lontano dista al più 1 da (0,0), per contare anche quelli che stanno sul bordo si è valutato se il vertice più vicino dista meno di 1 da (0,0).

P <- function(n) { min <- 0; mag <- 0; L <- 1/n for(i in 0:n) for(j in 0:n) { x <- i*L; y <- j*L; d <- x*x+y*y; if(i > 0 & j > 0 & d <= 1) min <- min+1; if(d < 1) mag <- mag+1 } A1 <- min/n^2*4; A2 <- mag/n^2*4; c(A1, A2) } P(10) #  2.68     3.44 P(100) #  3.1016     3.1796 P(1000) #  3.137548  3.145520 P(2000) #  3.139586  3.143579

    Dalle uscite si può congetturare che l'area sia π.

  Usando la proprietà additiva si poteva pensare il cerchio come l'unione del triangolo equilatero inscritto A sotto raffigurato, e dei triangoli isosceli B inscritti nelle 3 parti non coperte da A, e dei triangoli isosceli inscrivibili nelle 6 parti non coperte neanche da B (quelli che sono stati aggiunti per ottenere la figura sotto al centro), …:

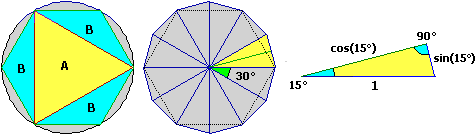
    Con la prima unione, in pratica, si passa da un triangolo equilatero a un esagono regolare (ossia con lati e angoli uguali), con la successiva si passa a un dodecagono regolare (raffigurato sopra al centro), poi a un poligono regolare a 24 lati, a 48 lati, … che tende a coincidere col nostro cerchio.
    Per calcolare l'area di uno di questi n-agoni basta (sempre per la proprietà additiva) calcolare l'area di uno degli n triangoli aventi un vertice nel centro in cui può essere scomposto l'n-agono e moltiplicarla per n. Sopra è illustrato come calcolarla nel caso del dodecagono: se considero come base il lato opposto al centro, i triangoli hanno base = 2·sin(15°) e altezza = cos(15°), e quindi area = sin(15°)·cos(15°). L'area del dodecagono è quindi 12·sin(15°)·cos(15°).
    Più in generale l'n-agono ha area  n · sin(360°/(2n)) · cos(360°/(2n)).
    Con un programma (ma si potrebbe benisimmo usare una semplice calcolatrice) si può, ottenere la successione di approssimazioni sotto riportata a sinistra (le uscite, arrotondate a 7 cifre, si stabilizzano rapidamente).

N.lati Area 3 1.299038 6 2.598076 12 3 24 3.105829 48 3.132629 96 3.13935 192 3.141032 384 3.141453 768 3.141558 1536 3.141584 3072 3.141591 6144 3.141592 12288 3.141593 24576 3.141593		P <- function(n) n*sin(pi/n)*cos(pi/n); v <- 13 n <- 3; for(i in 1:v){n <- n*2; print(c(n,P(n)))}

    Anche con questo metodo otteniamo valori che ci suggeriscono di congetturare che l'area sia π.
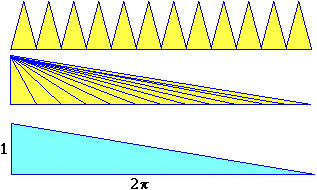
    La illustrazione sopra a destra spiega come convalidare questa congettura: il dodecagono considerato nell'illustrazione precedente può essere scomposto in 12 triangoli uguali, che possono essere trasformati in triangoli di uguale base e uguale altezza tali che la loro unione formi un triangolo della stessa altezza e avente come base il perimetro del poligono. Questo triangolo ha la stessa area del poligono. Posso ripetere questa trasformazione per ogni n-agono (a 24, 48, … lati). Man mano che raddoppio i lati del poligono la base di tale triangolo tende a coincidere con la lunghezza del cerchio (2π) e la sua altezza tende a coincidere con il raggio di esso (1), quindi tende a diventare un triangolo che ha area (2π·1)/2 = π.

Per inciso, ricordiamo che l'altezza degli n triangoli uguali in cui può essere scomposto un n-agono regolare (cioè la distanza dei lati dal centro) viene chiamata apotema. Per quanto osservato sopra, essa vale L/2/tan(360°/(2n)) se L è la lunghezza del lato (controlliamo la formula nel caso del quadrato: L/2/tan(360°/8) = L/2/tan(45°) = L/2: OK).

La determinazione dell'area di una figura approssimandola man mano meglio con una successione di poligoni che hanno i vertici sul suo contorno è chiamata metodo di esaustione. Il metodo è molto antico (risale a vari secoli avanti Cristo) ma il suo nome (dal verbo esaurire) risale al 1647.

    Si può anche ricavare l'area del cerchio in un modo più rapido (che è bene comunque si affianchi alle considerazioni precedenti, che consentono di introdurre considerazioni sui poligoni regolari) come quello utilizzabile nella scuola di base richiamato qui.

  Alla voce trasformazioni geometriche si è già osservato che le trasformazioni di scala moltiplicano le aree per il prodotto dei due fattori di scala: se una figura contiene Q quadratini, trasformandola ad esempio con la scala orizzontale H (le x vengono moltiplicate per H), l'area di ogni quadratino viene moltiplicata per H e quindi anche l'area della figura viene moltiplicata per H; se la figura subisce anche una trasformazione di scala verticale di fattore K, alla fine la sua area viene moltiplicata per H·K.

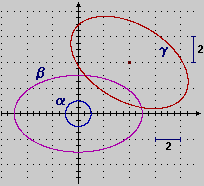L'ellisse β a lato è stata ottenuta dilatando orizzontalmente e verticalmente il cerchio α di raggio 1 con fattori moltiplicativi pari, rispettivamente, a 5 e a 3; sopra abbiamo visto che α ha area π; quindi β ha area 5·3π = 15π; γ, ottenuto da β con un movimento, ha la stessa area.     Nel caso di una trasformazione di scala monometrica (K = H), o più in generale di una similitudine, l'area viene moltiplicata per H2, se H è il fattore di scala.     Quindi un cerchio di raggio R, poiché è simile - con scala R - al cerchio di raggio 1, che ha area pari a π, ha area pari a πR2. [potrei dedurlo anche riferendomi alla figura precedente: se prendo 2πR come base del triangolo e R come altezza il loro semiprodotto è πR2]

    Un aspetto collegato è che se voglio esprimere in cm² un'estensione di 4 m² non devo moltiplicare 4 per 100 (il fattore di scala tra centimetri e metri) ma per 100² = 10000 (il numero di cm² che stanno in un m²).

  L'area di altre figure

Usando la proprietà additiva si possono determinare le aree di altre figure.
Ad es. la figura (1) a lato, detta segmento circolare, ha area pari a quella dello spicchio (settore) di cerchio di ampiezza α meno quella del triangolo avente due raggi e il segmento in comune con la figura come lati; l'area dello spicchio è πR2·α/360°; quella del triangolo è (vedi ) R2·sin(α/2)·cos(α/2).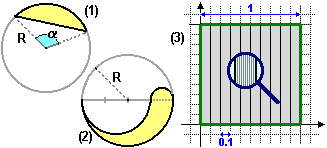
La fig. (2) è un semicerchio di raggio R più un semicerchio di raggio R/4 meno un semicerchio di raggio 3R/4, quindi ha area πR2·(1+1/16-9/16)/2 = πR2(1-1/2)/2 = πR2/4.     Ma non tutte le figure limitate (cioè racchiudibili in un rettangolo) hanno un'area. Ad es. in (3) è rappresentata la figura {(x,y) / 0≤x≤1, 0≤y≤1, x numero decimale limitato}: è una specie di quadrato costituito da infiniti segmenti verticali aventi per ascisse 0, 0.1, 0.2, … 0.9, 1, 0.01, 0.02, …, 0.09, 0.11, …, 0.19, …, 0.99, 0.001, …, 0.999, …. Questa figura non contiene quadrati di lato 1, né di lato 0.1, né di lato 0.01, né …; infatti ogni quadratino, per quanto piccolo, contiene dei punti con ascissa non decimale limitata. La figura ha dunque area 0?     Se consideriamo la figura {(x,y) / 0≤x≤1, 0≤y≤1, x numero non decimale limitato}, che unita alla precedente forma il quadrato {(x,y) / 0≤x≤1, 0≤y≤1}, con un ragionamento simile abbiamo che non può contenere alcun quadrato. Avrebbe allora anche questa area 0. Ma allora il quadrato, per la proprietà additiva, dovrebbe avere area 0+0=0, mentre sappiamo che ha area 1.     Dobbiamo concludere che queste figure sono di superficie non misurabile, altrimenti arriveremmo a una contraddizione.

Un tipo di figure a cui spesso si ricorre per determinare l'area di altre figure impiegando la proprietà additiva sono i trapezi. L'area di un trapezio è determinabile scomponendolo in due triangoli T1 e T2 nel modo illustrato a destra. Se b1 e b2 sono le misure di due lati paralleli del trapezio (le "basi" dei due triangoli) e h è la distanza tra le rette a cui appartengono (la "altezza" dei due triangoli), l'area del trapezio può essere espressa come: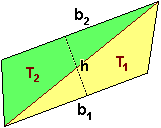
Area(T1) + Area(T2) = b1· h / 2 + b2· h / 2 = (b1+ b2) · h / 2
(espressione che può essere memorizzata verbalmente come "somma della basi per altezza diviso due").

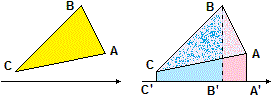Se di un triangolo conosco i vertici, posso facilmente determinarne l'area nel modo illustrato a lato: Area(ABC) = Area(A BC C' A') − Area(A C C' A') come differenza dell'area di due trapezi, di cui, come abbiamo visto, so calcolare l'area facilmente.

    Ecco una generalizzazione:  il calcolo dell'area di un poligono a partire dalle coordinate dei suoi vertici.  Riferendomi alla figura seguente, penso il poligono come ABCD come la figura HMABC a cui venga sottratta la figura MADCH, figure entrambe pensabili come unioni di trapezi:

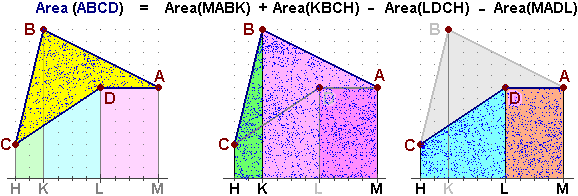
Se A = (11,8), B = (3,13), C = (1,3) e D = (7,8), facendo i calcoli tenendo conto che le "basi" sono date dalle ordinate e le "altezze" dai Δx, ottengo:
Area = (y_A+y_B)(x_A-x_B)/2 + (y_B+y_C)(x_B-x_C)/2 - (y_C+y_D)(x_D-x_C)/2 - (y_D+y_A)(x_A-x_D)/2 = ( (8+13)(11-3)+(13+3)(3-1)-(3+8)(7-1)-(8+8)(11-7) ) / 2 = 35
    Volendo, potevo prima manipolare simbolicamente la formula ottenendo:
Area = ((y_A+y_B)(x_A-x_B) + (y_B+y_C)(x_B-x_C) + (y_C+y_D)(x_C-x_D) + (y_D+y_A)(x_D-x_A)) / 2 =
( x_A(y_B-y_D) + x_B(y_C-y_A) + x_C(y_D-y_B) + x_D(y_A-y_C) ) / 2 = (11·5+3·(-5)+1·(-5)+7·5) / 2 = 35

    Questa formula per il calcolo dell'area (che ho ottenuto pensando il poligono sopra all'asse x) non cambia valore se traslo il poligono verticalmente, ossia se vario dello stesso numero tutte le y; infatti y_B-y_D, y_C-y_A, … restano invariati.  Quindi posso usarla anche se il poligono ha dei vertici sotto l'asse x.
    In modo ovvio posso estenderla per calcolare l'area di un generico poligono P₁P₂…P_n (con i vertici elencati in senso antiorario):

Area = ( (y₁+y₂)(x₁-x₂) + (y₂+y₃)(x₂-x₃) + … + (y_n+y₁)(x_n-x₁) ) / 2
Area = ( x₁(y₂-y_n) + x₂(y₃-y₁) + x₃(y₄-y₂) + … + x_n(y₁-y_n-1) ) / 2

    Ovviamente, la formula precedente vale anche se scambio le "x" con le "y":  se ribalto la figura attorno alla bisettrice del primo quadrante non ne cambio l'area.

I calcoli sono fattibili facilmente con R. Vediamo il caso del poligono precedente:
x <- c(11, 3,1,7)
y <- c( 8,13,3,8)
n <- length(x); area <- (y[n]+y[1])*(x[n]-x[1])
for (i in 1:(n-1)) area <- area + (y[i]+y[i+1])*(x[i]-x[i+1]); area <- area/2
area
[1] 35
    Qui come calcolare l'area della penisola italiana

    I calcoli sono fattibili anche da rete usando questo semplicissimo script:

    Vedi qui per calcolare, con una formula simile, il centroide di un generico poligono.

    Vedi qui e qui come fare calcoli simili una volta azionato  source("http://macosa.dima.unige.it/r.R").

    L'estensione di un triangolo dipende dalle dimensioni dei suoi lati.  Oltre che trovare l'area facendo "base·altezza/2"  (o usando, come appena visto, le coordinate dei suo vertici)  posso trovarla con una formula che dipende dalle misure a, b, c dei lati.  Senza dimostrarla, ricordiamo che essa è  Area = √((a+b+c)·(a+b-c)·(a−b+c)·(−a+b+c))/4  (è nota come formula di Erone - scienziato greco del I sec. d.C. - ma era già nota prima di lui).  Il termine sotto radice può essere ricordato come il prodotto tra il perimetro e i tre valori che si ottengono sottraendo un lato dalla somma degli altri due.  Limitiamoci a vedere che vale nel caso del triangolo rettangolo:
• se c²=a²+b², √( (a+b+c)·(a+b−c)·(a−b+c)·(−a+b+c) )/4 = √( ((a+b)²−c²)·(c²−(a−b)²)) )/4 = √(2ab·2ab)/4 = a·b/2
    Da essa possiamo ricavare direttamente, in altro modo, la formula per l'area del triangolo equilatero:
• se a=b=c=L, √( (a+b+c)·(a+b−c)·(a-b+c)·(−a+b+c) )/4 = √( 3·L·L·L·L )/4 = √3/4·L²
   Qui trovi come usare il comando AREAT per fare rapidamente questo calcolo con R, dopo aver azionato source("http://macosa.dima.unige.it/r.R").

Esercizi:  testo  e  soluzione,  testo  e  soluzione,  testo  e  soluzione,  testo  e  soluzione,  testo  e  soluzione.

 altri collegamenti     [nuova pagina]