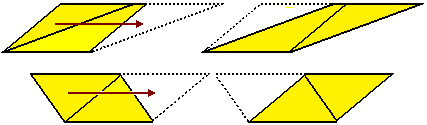
Area parallelogrammi
Oltre che nei modi visti qui, che l'area di un parallelogramma è la stessa di un rettangolo con la stessa base e la stessa altezza puņ essere dimostrato nel modo seguente, un po' meno intuitivo.
Nei casi come i seguenti, in cui spostando con un movimento piano la base di un parallelogramma su quella dell'altro i lati opposti alle due basi abbiano un segmento o un punto in comune, si puņ dimostrare che i due parallelogrammi sono eguali in quanto unioni di parti eguali.

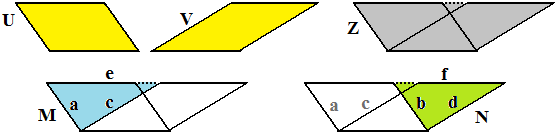
Nel caso in cui ciņ non accada, considero la figura Z ottenuta spostando nel modo detto sopra un parallelogramma, V, sull'altro, U,
in modo che le basi coincidano e che i lati opposti siano allineati.
I triangoli M ed N sotto evidenziati sono eguali in quanto hanno tutti e tre i
lati eguali, a = b e c = d in quanto lati opposti di un parallelogramma, e = f in quanto si ottengono entrambi aggiungendo lo stesso segmento
a due segmenti che sono eguali essendo entrambi eguali al lato di base.
Quindi hanno la stessa area.
Se dalla figura Z tolgo ora l'uno ora l'altro ottengo V e U, che sono dunque eguali.
In molti libri di testo vi è una dimostrazione come la seguente, tratta da un famoso libro di testo (di Virgino Vercelli) della fine del XIX secolo, in cui si considera solo il primo caso.
