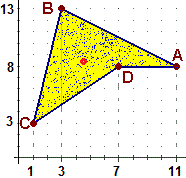
Ricordiamo come calcolare l'area di un poligono P1P2…Pn a partire dalle coordinate dei suoi vertici (elencati in senso antiorario). Area = ( (y1+y2)(x1-x2) + (y2+y3)(x2-x3) + … + (yn+y1)(xn-x1) ) / 2 Riferiamoci alla figura a lato. Supponiamo che A = (11,8), B = (3,13), C = (1,3) e D = (7,8). Facendo i calcoli con R: |  |
x <- c(11, 3,1,7)
y <- c( 8,13,3,8)
n <- length(x); area <- (y[n]+y[1])*(x[n]-x[1])
for (i in 1:(n-1)) area <- area + (y[i]+y[i+1])*(x[i]-x[i+1]); area <- area/2
area
[1] 35
Il centroide C si può dimostrare (cerca "polygon centroid Surveyor's Formula" con un motore di ricerca) che è:
C
C
Facendo i calcoli con R:
cx <- (x[n]+x[1])*(x[n]*y[1]-x[1]*y[n]); cy <- (y[n]+y[1])*(x[n]*y[1]-x[1]*y[n])
for (i in 1:(n-1)) {
cx <- cx + (x[i]+x[i+1])*(x[i]*y[i+1]-x[i+1]*y[i]);
cy <- cy + (y[i]+y[i+1])*(x[i]*y[i+1]-x[i+1]*y[i]) }
cx <- cx/(area*6); cy <- cy/(area*6)
cx; cy
# 4.619048
# 8.47619
Il calcolo per determinare il centroide di una figura poligonale è comunque già incoportato
nel file richiamabile con
Vediamo, per curiosità, come trovare il centroide della penisola italiana.
source("http://macosa.dima.unige.it/r.R")
# Vediamo come esaminare il contenuto di un file:
readLines("http://macosa.dima.unige.it/R/penisola.txt",n=4)
# comando la visualizzazione delle prime 4 righe del file "penisola.txt". Ottengo:
# "# penisola italiana" "8,46" "7.87,45.9" "7.6,45.95"
# Capisco che il file è una tabella di coppie di dati preceduta da un commento.
# Metto la tabella in un file (chiamiamolo "T") col seguente comando, in cui
# specifico che devo saltare (skip) una riga (il commento) e che i dati
# sono separati da ",":
T <- read.table("http://macosa.dima.unige.it//R/penisola.txt",skip=1,sep=",")
# Non stampo la tabella per non occupare spazio; la visualizzo con:
data.entry(T) # Compare la finestra seguente che poi chiudo:
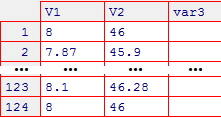# Le due colonne di dati sono chiamate V1 e V2. Le metto in X e Y con:
X <- tab$V1; Y <- tab$V2
box(min(X),max(X), min(Y),max(Y)); spezzaC(X,Y, "green"); spezza(X,Y, "red")
puntino(centroP[1],centroP[2], "red")
centroP
# 12.18996 43.48932
# l'"area" usando come unità di misura i "quadri" delimitati da
# longitudini e latitudini
areaP
# 28.59358
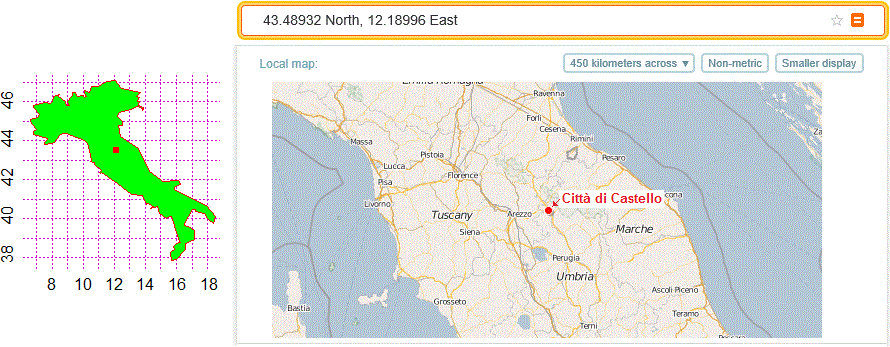
Con WolframAlpha vedo che il centro corrisponde a Città di Castello:
Vediamo, come altro esempio, la determinazione del centroide di un semicerchio, approssimando il contorno con un poligono di moltissimi lati:
source("http://macosa.dima.unige.it/r.R")
x <- seq(1,-1,len=1e5)
y <- sqrt(1-x^2)
n <- length(x)
boxm(-1,1, -0.5,1.5)
spezzaC(x,y,"yellow")
areaP
# 1.570796 (è π/2)
punto(centroP[1],centroP[2], "blue")
centroP[2]
# 0.4244132
centroP[2]/pi
centroP[2]*pi
# 1.333333
frazio(centroP[2]*pi)
# 4/3 [ è 4/(3·π) ]
|  |
Il centroide è il punto (0, 0.4244132). Con il calcolo integrale (vedi)
si può trovare che esso è esattamente