Covarianza e correlazione
Correlazione tra variabili casuali
Covarianza e correlazione
Alla voce 
sistemi di variabili casuali abbiamo visto
esempi di variabili X e Y, come ascissa e ordinata dei punti di un bersaglio che vengono colpiti,
che non sono stocasticamente indipendenti ma che, tuttavia, danno luogo a un diagramma di dispersione
in cui non viene privilegiata alcuna direzione, e altri, alla fine della voce, in cui i punti tendono
a disporsi lungo una linea obliqua, ossia in cui, all'aumentare di X, Y tende ad aumentare più o meno proporzionalmente. Per distinguere queste situazioni, in entrambe delle quali X e Y sono dipendenti, si dice che X e Y nel secondo caso sono correlate, nel primo no.
Per "misurare" la tendenza delle due variabili a variare proporzionalmente si usa il concetto di covarianza, che deriva il suo nome dalla parentela con la formula della varianza: al posto del quadrato dello scarto di una variabile si prende il prodotto dei due scarti:
V(X) = M( (X–M(X))2 )
V(Y) = M( (Y–M(Y))2 ) covarianza: Cov(X,Y) = M( (X–M(X)) (Y–M(Y)) )
Nel caso sperimentale questo termine diventa: Σ i=1..n (Xi–Mn(X))(Yi–Mn(Y)) / n
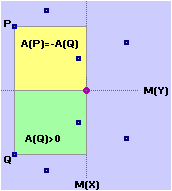
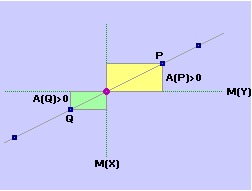
La formula può essere motivata in vari modi. Ad es. si può interpretarla come un indicatore che assume un valore assoluto che scende quanto più i punti tendono a disporsi in modo da presentare una simmetria verticale o orizzontale e che cresce quanto più i punti tendono a disporsi lungo una retta obliqua. Infatti le componenti della sommatoria rappresentano aree "con segno" di rettangolini che hanno come dimensioni le distanze "con segno" delle coordinate dei punti dalle coordinate del baricentro. Nella figura sotto a sinistra (simmetria orizzontale) le componenti della sommatoria due a due si annullano, per cui la covarianza è nulla. Se schiaccio obliquamente la nuvola di punti la compensazione diventa solo parziale. Nella caso della figura a destra (X e Y in relazione lineare) non c'è alcuna compensazione (componenti tutte positive).
Il segno sarà uguale al segno della pendenza della retta lungo cui i punti tendono a disporsi.
Se X e Y sono indipendenti, ci aspettiamo che la covarianza sia nulla. E infatti:
Cov(X,Y) = M( (X–M(X)) (Y–M(Y)) )
= M((X–M(X)))·M((Y–M(Y))) = 0·0 = 0.
L'interpretazione geometrica ci facilita la comprensione che
M( (X–M(X))(Y–M(Y)) ) è 0 anche nel caso in cui fissando diversi valori di X la Y continua
a variare in modo "analogo" attorno sempre allo stesso valor medio, e, viceversa,
Un'altra possibile interpretazione è basata sull'osservazione
che Cov(X,Y) =
Per non tener conto delle unità di misura in cui sono espressi X e Y (e per passare da un'"area" a un numero puro) la covarianza viene normalizzata dividendo per gli s.q.m. di X e Y, introducendo il:
| coefficiente di correlazione: r X,Y = |
|
= |
|
L'interpretazione geometrica con cui abbiamo introdotto la covarianza fa supporre che se X
e Y sono dipendenti deterministicamente e legate da una relazione lineare Y = aX + b il coefficiente di
correlazione assuma valore assoluto massimo. Ciò può effettivamente essere dimostrato
(la dimostrazione non è complicata, ma la omettiamo).
Si ricava facilmente, usando le proprietà della media, che
in questo caso 
vedi].
Quindi in generale –1 ≤
Nota. Come abbiamo visto, "σ" può essere stimato usando come denominatore "n−1" invece che "n". Una cosa analoga accade per la covarianza. Dato che il coefficiente di correlazione si ottiene come rapporto in cui compaiono a numeratore e a denominatore covarianza e "σ", per esso non ci sono ambiguità: sia in un caso che nell'altro si ottiene lo stesso valore.
Un esempio. Limiti e usi distorti della correlazione.
A questo punto proviamo ad impiegare il programma R per analizzare coppie (e n-uple) di variabili casuali (ma potremmo usare anche altri programmi). Come nel caso "univariato", i dati possono essere introdotti direttamente o essere letti da file, in cui le righe (record) indicano i soggetti su cui si è effettuato il rilevamento e le colonne (campi) indicano le variabili casuali (o modalità) rilevate.
Ecco, ad es., la parte iniziale del file battito.txt:
# Indagine sugli studenti di un corso universitario, dal manuale di MiniTab # battiti prima di eventuale corsa di 1 min # battiti dopo # fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta) # fumatore (1 si`;0 no) # sesso (1 M; 2 F) # altezza # peso # attivita` fisica (0 nulla;1 poca;2 media; 3 molta) Num,BatPrima,BatDopo,Corsa,Fumo,Sesso,Alt,Peso,Fis 01,64,88,1,0,1,168,64,2 02,58,70,1,0,1,183,66,2 ...
Se raccolti su un foglio di calcolo i dati assumerebbero questo aspetto:
| bat | bat.dopo | corsa | fumo | sesso | alt | peso | attiv |
| 64 | 88 | 1 | 0 | 1 | 168 | 64 | 2 |
| 58 | 70 | 1 | 0 | 1 | 183 | 66 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
Potremmo copiare il file sul nostro computer o esaminarlo direttamente da rete. In R
con:
nome <- "http://macosa.dima.unige.it/om/voci/bivar/battito.txt"
readLines(nome,n=12)
vedrei le prime righe del file e potrei poi caricare i dati azionando
dati <- read.table(nome,skip=9,header=TRUE,sep =",")
con cui li metto in una tabella, specificando di saltare 9 righe, che c'è un'intestazione
con i nomi dei campi e che i dati sono separati da ",".
Un modo comodo per avere un'idea del file senza stampare tutti i dati (che potrebbero essere molti)
è usare il comando
str(dati)
Con cui ottengo
'data.frame': 92 obs. of 9 variables: $ Num : int 1 2 3 4 5 6 7 8 9 10 ... $ BatPrima: int 64 58 62 66 64 74 84 68 62 76 ... $ BatDopo : int 88 70 76 78 80 84 84 72 75 118 ... $ Corsa : int 1 1 1 1 1 1 1 1 1 1 ... $ Fumo : int 0 0 1 1 0 0 0 0 0 0 ... $ Sesso : int 1 1 1 1 1 1 1 1 1 1 ... $ Alt : int 168 183 186 184 176 184 184 188 184 181 ... $ Peso : int 64 66 73 86 70 75 68 86 88 63 ... $ Fis : int 2 2 3 1 2 1 3 2 2 2 ...
I dati sono stati rilevati durante una lezione di un corso universitario (almeno così viene detto in un manuale del software statistico MiniTab da cui essi sono stati tratti e parzialmente rielaborati – per presentarli nel sistema metrico decimale). La colonna "battiti dopo" si riferisce a un secondo rilevamento del battito cardiaco effettuato dopo che gli studenti a cui (lanciando una moneta) è uscito testa (1 nella colonna "corsa") hanno fatto una corsa di un minuto.
Col comando summary posso avere una informazione sintetica di tutte le variabili; ma la prima colonna contiene solo il numero d'ordine, quindi invece di usare summary(dati) esamino solo le colonne dalla 2 alla 9 con:
summary(dati[2:9])
BatPrima BatDopo Corsa Fumo
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
Sesso Alt Peso Fis
Min. :1.00 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.00 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.00 Median :175.0 Median :66.00 Median :2.000
Mean :1.38 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.00 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.00 Max. :190.0 Max. :97.00 Max. :3.000
Come analizzare un singolo campo e suoi sottocampi:
datiF <- subset(dati,dati$Sesso==2); datiM <- subset(dati,dati$Sesso==1)
h <- dati$Alt; hM <- datiM$Alt; hF <- datiF$Alt
int <- seq(150,200,5); Y <- c(0,0.06)
griglia <- function(x) abline(v=axTicks(1), h=axTicks(2), col=x,lty=3)
par(mfrow=c(1,3), mar=c(3,3,2,1))
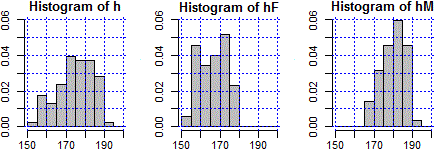
hist(h,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hF,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hM,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
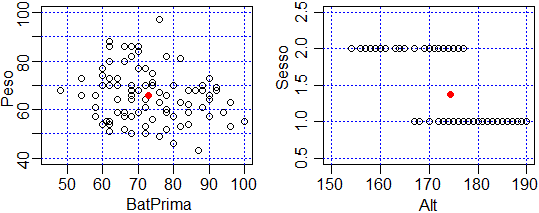
Ecco i diagrammi di dispersione di due coppie di variabili, in un caso entrambe "continue", nell'altro una continua e l'altra discreta; in un caso a bassa correlazione ("nuvola" di punti leggerissimamente inclinata con pendenza negativa), nell'altro ad alta (essendo una discreta, a 2 valori, i punti si distribuiscono su due strisce, ma si vede che l'andamento è "decrescente": correlazione, come vediamo subito dopo, vicina a -1). I punti evidenziati in rosso sono i baricentri dei sistemi di punti rappresentati (alcuni conteggiati più volte).
# Chiudi la finestra precedente o aprine una nuova con dev.new()
plot(c(45,100),c(40,100),type="n",xlab="BatPrima", ylab="Peso")
griglia("blue")
points(dati$BatPrima,dati$Peso)
points(mean(dati$BatPrima),mean(dati$Peso),pch=19,col="red")
#
plot(c(150,190),c(0.5,2.5),type="n",xlab="Alt", ylab="Sesso")
griglia("blue")
points(dati$Alt,dati$Sesso)
points(mean(dati$Alt),mean(dati$Sesso),pch=19,col="red")
Ecco la matrice di correlazione, che sintetizza le correlazioni tra tutte le diverse variabili di "battito" [avrei potuto battere solo cor(dati[2:9]) ottenendo valori di 8 cifre; con print(…,2) posso "accorciare" i valori; avrei potuto usare, con esiti diversi, round(…,3)]:
print(cor(dati[2:9]),2)
BatPrima BatDopo Corsa Fumo Sesso Alt Peso Fis
BatPrima 1.000 0.616 0.0523 0.129 0.29 -0.211 -0.203 -0.0626
BatDopo 0.616 1.000 0.5768 0.046 0.31 -0.153 -0.166 -0.1411
Corsa 0.052 0.577 1.0000 0.066 -0.11 0.224 0.224 0.0073
Fumo 0.129 0.046 0.0656 1.000 -0.13 0.043 0.201 -0.1202
Sesso 0.285 0.309 -0.1068 -0.129 1.00 -0.709 -0.710 -0.1050
Alt -0.211 -0.153 0.2236 0.043 -0.71 1.000 0.783 0.0893
Peso -0.203 -0.166 0.2240 0.201 -0.71 0.783 1.000 -0.0040
Fis -0.063 -0.141 0.0073 -0.120 -0.10 0.089 -0.004 1.0000
Tra altezza e peso vi è un alto coefficiente di correlazione: 0.78. Se ci restringiamo a una sottopopolazione più omogenea (quella femminile o quella maschile, che hanno pesi e altezze con medie abbastanza diverse), ci potremmo aspettare di ottenere un coefficiente maggiore. Ma se estraiamo la popolazione femminile otteniamo 0.52. Perché?
cor(dati[7],dati[8])
Peso
Alt 0.7826331
cor(subset(dati[7],dati$Sesso==1),subset(dati[8],dati$Sesso==1))
Peso
Alt 0.5904648
cor(subset(dati[7],dati$Sesso==2),subset(dati[8],dati$Sesso==2))
Peso
Alt 0.5191614
Se traccio in rettangoli cartesiani uguali, i grafici di dispersione
par(mfrow=c(1,3), mar=c(3,3,2,1))
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(dati$Alt,dati$Peso)
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==1),subset(dati$Peso,dati$Sesso==1),col="blue")
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==2),subset(dati$Peso,dati$Sesso==2),col="red")
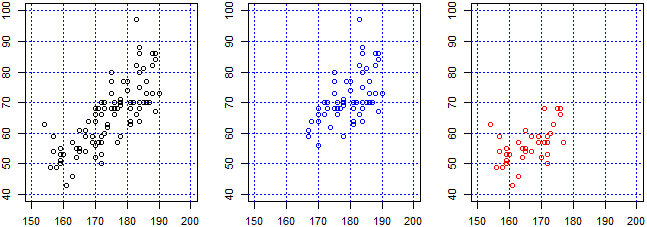
Questo esempio mette in luce come le statistiche che si ottengono sono spesso ingannevoli. In casi come questo, abbastanza frequenti, il problema è dovuto alla presenza di due sottopopolazioni con caratteristiche differenti.
Un altro problema è legato al fatto che le statistiche ottenute su una certa popolazione possono essere utilizzate considerando questa come un campione di una popolazione più estesa. In tal caso alle statistiche ottenute occorre associare degli
intervalli di confidenza e, se il campione è piccolo, devono essere opportunamente corrette.
Anche nel caso della covarianza, come in quello della varianza, per avere uno stimatore non distorto del valore riferito alla eventuale popolazione "limite", occorre moltiplicare per n/(n–1), essendo n la numerosità del campione.
La determinazione di intervalli di confidenza è più complicata.
Osserviamo, ad es., che nel caso della correlazione 0.52 tra Altezza e Peso tra le femmine del file "battito" si otterrebbe
[0.22, 0.73] come intervallo di confidenza al 95%, e dovrei tenerne conto se volesi usare questi dati per individuare la
correlazione tra altezza e peso dell'intera popolazione femminile. Ecco come potrebbe essere svolto questo
calcolo con R:
# devo trasformare le liste dei dati in un puri vettori
x <- subset(dati[7], dati$Sesso==2); x <- unlist(x)
y <- subset(dati[8], dati$Sesso==2); y <- unlist(y)
cor.test(x,y, conf.level = 0.95)
95 percent confidence interval:
0.2248088 0.7266851
sample estimates: cor 0.5191614
Infine, come già osservato
( vedi), occorre tener conto che quelle individuate sono solo relazioni statistiche, non di causa-effetto: mentre nel caso della correlazione
tra le colonne "battito dopo" e "corsa" di "battito"
c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco), il fatto che emerga una correlazione positiva tra il "peso" e l'essere stata sorteggiata la "corsa" non significa che ci sia qualche fattore fisico che faccia sì che l'uscita di testa sia influenzata dalla massa della persona.
Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.
Rette di regressione. Assi principali.
[i paragrafi seguenti sono in via di rielaborazione]
Di fronte a dati sperimentali relativi a un sistema (X,Y) per cui si ritiene che Y vari in funzione di X, si può cercare di trovare una funzione F tale che il suo grafico approssimi i punti sperimentali.
In curve approssimanti questo problema è affrontato nel caso in cui X sia una variabile deterministica. È simile il modo in cui si affronta il caso in cui X sia casuale.
In base ai dati (con una delle tecniche viste in
curve approssimanti) e, possibilmente, in base
a considerazioni teoriche, si cerca di individuare il tipo di funzione (lineare, polinomiale, esponenziale, …) che
si vuole utilizzare. Se si ipotizza che ci sia una relazione lineare che esprima Y in funzione di X, e non
si hanno altre informazioni, la tecnica in genere usata è quella dei minimi quadrati (già
impiegata per introdurre la variabile χ2).
Illustriamola su un semplice esempio.
In generale, nel caso di n rilevamenti (Xi, Yi) di due variabili casuali X e Y, posso approssimare la dipendenza di Y da X con una relazione Y = kX con k =
Nota. • Questa formula è facile da ricavare, ma anche da ricordare, pensando che "dimensionalmente" deve essere equivalente a Y/X (e questa lo è avendo le dimensioni di XY/X2) e che deve dipendere anche da come variano congiuntamente X e Y (e questa dipende da XY, ossia dai prodotti XiYi).
• Se avessi imposto che la retta passasse per (p,q) invece che per O avrei potuto effettuare
lo stesso calcolo traslando i dati di
| Un esempio concreto.
Consideriamo il file terraria.tab
in cui sono contenute un po' di coppie |
 |
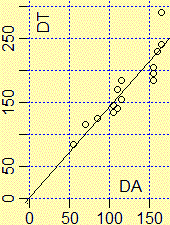Se studiamo il file con R (qui
come fare facilmente i calcoli) troviamo innanzi tutto c'è un alto coeff. di correlazione (0.91) tra DT e DA.
Lo stesso programma ci permette di calcolare automaticamente e rappresentare (vedi figura a lato) la retta
Negli esempi precedenti abbiamo cercato una F: x → ax+b per cui sia minimo
| aX,Y = |
|
= |
|
bX,Y = M(Y) – aX,YM(X) |
|
Le scritture aX,Y e bX,Y ricordano il fatto che si sta pensando Y come funzione di X. La retta y = aX,Y x + bX,Y viene detta retta di regressione
(aX,Y è chiamato coefficiente di regressione); passa per il "baricentro" (M(X), M(Y)): vedi la figura a lato, in cui il pallino marrone è il
baricentro dei punti che rappresentano i dati. Le stesse formule vengono impiegate anche nel caso teorico e possono essere motivate direttamente con altre argomentazioni. All'aumentare dei rilevamenti le rette di regressione sperimentali tendono (con una convergenza in probabilità) a coincidere con la retta di regressione teorica. |
 |
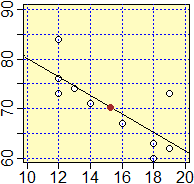Analogamente si avranno aY,X e bY,X se si pensa X in funzione di Y.
Se Y e X sono in relazione lineare le rette y = aX,Y x + bX,Y e x = aY,X y + bY,X ovviamente coincidono.
Se Y e X sono indipendenti o totalmente scorrelate, le due rette sono parallele agli assi coordinati (aY,X e aY,X sono 0 essendo tale la covarianza).
Ecco, ad esempio, le rette due rette di regressione per delle cadute
di proiettili distribuite come si è visto in
sistemi di variabili casuali (vedi qui come ottenerle).
È possibile tracciare anche
la retta che "meglio approssima" i punti quando lo scarto da essi sia misurato con la sommatoria dei quadrati delle distanze
dei punti sperimentali dalla retta (le rette di regressione sono invece ottenute considerando non le distanze, ma le loro
proiezioni, orizzontali o verticali). Questo si ottiene chiedendo il tracciamento degli assi principali
di dispersione: questa retta, passante anch'essa per il baricentro, e la sua perpendicolare nel baricentro vengono
chiamate così perché per alcune elaborazioni statistiche vengono assunte come nuovo sistema di riferimento
(per facilitare calcoli e forme di ragionamento).
Esse corrispondono agli assi di simmetria delle curve di livello della superficie considerata
nella voce
sistemi di variabili casuali. Vedi qui come
determinarle usando R.
È facile verificare che
In altre parole, il coefficiente di correlazione è uguale, in valore assoluto, alla media geometrica dei due coefficienti di regressione. Ciò conferma che quanto più le due rette di regressione sono vicine tanto più le due variabili sono correlate, positivamente o negativamente: quanto più ciò accade tanto più i due coefficienti di regressione tendono ad essere uno il reciproco dell'altro (infatti da y=ax+… segue x=1/a·y+…) e quindi la loro media geometrica tende ad essere 1.
Anche per la regressione valgono considerazioni analoghe a quelle
svolte per la stima
della correlazione teorica. R fornisce anche intervalli di confidenza per i coefficienti di regressione e
per le coordinate del baricentro, dai quali, volendo, si possono trovare intervalli di confidenza anche
per bX,Y e bY,X. Vedi gli esercizi
6a.5 e 6.31.
Ancora un esempio
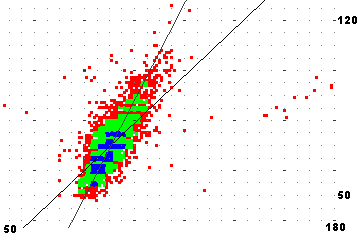
Ecco alcune analisi del file leva.tab, in cui sono contenuti i valori del torace (in cm), del peso (in kg), della regione di nascita (ordinata per latitudine del capoluogo) e della statura (troncata ai centimetri e diminuita di 100). Confronto di coefficienti di correlazione, grafici di dispersione e coppie delle rette di regressione di (statura, peso) e (torace, peso) rappresentati in due sistemi monometrici (la diversa divaricazione delle rette di regresso suggerisce il diverso livello di correlazione) [qui come fare l'elaborazione con R]
 |
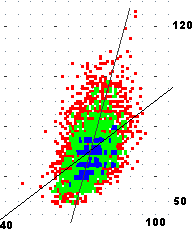r(S,P) = 0.4581852 M(S) = 74.42326 min: 47 max: 96 M(P) = 70.47674 min: 48 max: 126 y=ax+b a=0.7664956 b=13.43164 x=ay+b a=0.2738877 b=55.12055 |
r(T,P) = 0.6974944 M(T) = 91.18753 min: 48 max: 179 M(P) = 70.47674 min: 48 max: 126 y=ax+b a=0.940987 b=-15.32954 x=ay+b a=0.5170087 b=54.75044 |
 |
| Osserviamo come, di fronte a grandi quantità di dati, l'uso di un istogramma in forma poliedrica, come quello a destra, consente di integrare le informazioni che si possono ricavare dal diagramma di dispersione (nel quale non si riescono a distinguere le zone più fitte in quanto i punti si sovrappongono, anche se in alcuni programmi, come nel caso di R, ciò viene realizzato con un cambiamento nel colore dei punti). Sotto a destra è riportato un istogramma (non normalizzato) del campo "pesi"; si vede bene la forma non gaussiana. |  |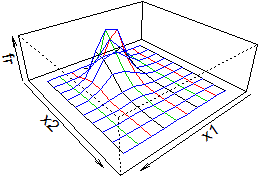
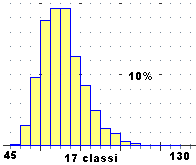 | Analisi del campo Pesi 4170 dati in 4170 righe min,max: 48,126 media: 70.4767386 mediana: 70 5% :55 25% :63 50% :70 95% :90 75% :76 percentili ----|--|===|=|------|----------------- |
Un esempio di analisi di dati sperimentali (Grandezza1 in funzione di Grandezza2)
Consideriamo un esempio relativo a dati dotati di precisione.
|
Per studiare le caratteristiche di un elastico, lo si tiene sospeso per un estremo e si appendono all'altro estremo diversi oggetti. Ogni volta si misura il peso dell'oggetto e il corrispondente allungamento dell'elastico. Il peso F degli oggetti viene misurato con una bilancia a molla con divisioni di 10 g (in modo che se l'ago si ferma vicino alla tacca 220 si può assumere che il peso sia 220±5 g). Le lunghezze che assume l'elastico vengono misurate con la precisione di 1 mm, in modo che i valori dell'allungamento H (ottenuti come differenza di due lunghezze) hanno la precisione di 2 mm. Si ottengono i valori riportati nella tabella a fianco. Ipotizzando che, nell'intervallo di valori considerato, la relazione tra lunghezza dell'elastico e peso sia lineare, vogliamo trovare k tale che F=H·k. |  |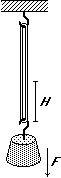
Sotto sono indicati altri due possibili procedimenti.
|
(a) Rappresentare i rettangoli che sono il prodotto degli intervalli di indeterminazione delle varie coppie di dati e trovare graficamente un intervallo di indeterminazione per k (si cercano le rette passanti per (0,0) e per tutti i rettangolini di minima e di massima pendenza).
(clicca l'immagine a destra per ingrandirla) |
|
||||||||||||||
Ecco come ottenere il grafico con R:
H <- c(11,16,30,47); F <- c(220,350,590,940)
eH <- 2; eF <- 5
plot(c(-1,50),c(-10,1000),type="n",xlab="", ylab="")
abline(h=0,v=0); abline(h=seq(100,1000,100),v=seq(5,50,5),lty=3)
rect(H-eH,F-eF,H+eH,F+eF)
library(MASS)
p1 <- min(fractions((F+eF)/(H-eH))); p1
21
p2 <- max(fractions((F-eF)/(H+eH))); p2
115/6
fm <- function(H) p1*H; fM <- function(H) p2*H
plot(fm,0,50,add=TRUE,col="blue"); plot(fM,0,50,add=TRUE,col="blue")
(b) Calcolare gli intervalli di indeterminazione dei valori F/H relativi alle quattro prove, cioè: [215/13,225/9] = [16.538…,25], [345/18,355/14] = [19.166…,25.357…], … e farne l'intersezione.
Si riottiene, ovviamente, lo stesso intervallo ottenuto con il metodo (a).
Potevo anche ottenere sia il grafico che l'equazione delle due rette ricorrendo alla libreria accessibile con source("http://macosa.dima.unige.it/r.R").
H <- c(11,16,30,47); eH <- c(2,2,2,2) F <- c(220,350,590,940); eF <- c(5,5,5,5) box(0,50,0,1000); puntiapp(0,0, H,F, eH,eF) # 19.16667 * x 21 * x
Non avrebbe senso ricorrere
alla retta di regressione in quanto non verrebbero utilizzate le informazioni sulla precisione delle misure.
Poi non si terrebbe conto del "punto esatto"
Nota 1.
Abbiamo considerato solo il caso della approssimazione con funzioni lineari. Nel caso
di altri andamenti ci si può, spesso, ricondurre al caso lineare mediante opportune trasformazioni dei
dati (realizzabili con R, con un foglio di calcolo o con un altro programma). Esistono, comunque, numerose
tecniche, che dipendono dai modi in cui sono stati raccolti i dati di cui si dispone, dalle altre informazioni che abbiamo
sulle funzioni che vogliamo li approssimino, …. Piuttosto che imparare alcune ricette (o adattarsi alle
poche elaborazioni che è in grado di fare "direttamente" un foglio di calcolo), è bene,
quando si hanno una serie di dati da analizzare, rivolgersi a chi ha esperienze e conoscenze sull'argomento.
L'obiettivo di questi "appunti", come di quello di ogni altra forma di trasmissione delle conoscenze, non è
dare delle risposte definitive su tutti gli argomenti trattati, ma dare delle risposte che, spesso, sono parziali
e provvisorie, e potranno essere integrate in eventuali studi successivi. È importante rendersi conto
di questa incompletezza.
Per dare un'idea delle tecniche che si possono impiegare, consideriamo un
esempio semplice, che, comunque, si riferisce a situazioni abbastanza diffuse.
Un oggetto, pesante e di forma compatta, viene lasciato cadere e ne viene misurata,
mediante una successione di immagini fotografiche scattate
ogni decimo di secondo, l'altezza in cm da terra. Supponiamo che in corrispondenza
dei tempi di 1, 2, 3, 5 decimi di secondo (rilevati con errori trascurabili)
si registrino, in ordine, le altezze da terra di 131, 113, 89 e 7 centimetri,
arrotondate tutte con la stessa precisione, ad esempio di 1 centimetro.
In situazioni di questo genere, in cui si conoscono le coordinate di N
punti sperimentali con ascisse xi note esattamente e con ordinate yi
della stessa indeterminazione, si può ricorrere ad un procedimento che
impiega tecniche probabilistiche di vario tipo (simili a quelle considerate per trovare le rette
di regressione, e che rientrano nella cosiddetta "regressione polinomiale"), per arrivare alla determinazione dei coefficienti
della funzione polinomiale di grado 2 che "con maggiore probabilità" approssima i
punti noti. Senza entrare nei dettagli di esso, si ottiene che si tratta della
funzione
A·N + B·Σxi + C·Σxi2 = Σyi
A·Σxi + B·Σxi2 + C·Σxi3 = Σxiyi
A·Σxi2 + B·Σxi3 + C·Σxi4 = Σxi2yi.
In questo link
trovi come svolgere questo calcolo (e calcoli analoghi) con R. Ottieni le soluzioni:
A = 137.327273, B = −1.945455, C = −4.818182,
a cui corrisponde la seguente rappresentazione grafica:
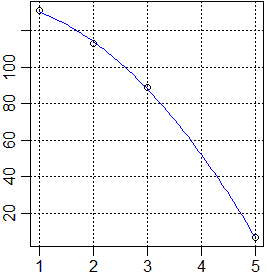
Per i dati raffigurati sopra a destra si ottiene (vedi)
che il coefficiente di correlazione lineare è nullo (sono punti simmetrici rispetto
ad un asse verticale) mentre che quello di 2° grado è 1.
In quest'altro link puoi trovare come
calcolare un coefficiente di correlazione per la regressione polinomiale anche nel caso dei polinomi
3º grado.
Nota 2.
Il coefficiente di correlazione a cui abbiamo fatto riferimento qui (indicato con
r) si chiama di
Pearson. Quando si parla di correlazione senza specificazioni ci si riferisce ad esso.
Ci sono due altri coefficienti di correlazione spesso usati, noti come di Sperman (ρ) e
di Kendall (τ). Ci occupiamo velocemente solo del primo.
Viene indicato con ρ (la lettera greca "ro", che corrisponde alla nostra R) in quanto
confronta i "ranghi" dei dati, cioè non i loro valori ma il loro numero
d'ordine (1º, 2º, …); per informazioni più dettagliate
cerca Spearman rank correlation coefficient in WolframAlpha. Con R possiamo
calcolarlo usando cor(x,y,method="spearman"). Un esempio.
|
x <- c(10,20,30,40) y <- c(15,60,70,200) cor(x,y) # 0.9173057 cor(x,y,method="spearman") # 1 I dati precedenti sono disposti in modo crescente, ma non allineati. L'usuale coefficiente di correlazione (ossia quello di Pearson) è vicino ad 1, ad indicare il fatto che i dati stanno in una nuvoletta quasi rettilinea. Il coefficiente di Spearman è invece proprio 1, ad indicare che i dati sono crescenti, al di là del modo con cui crescono. |
 |
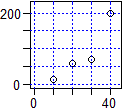Approfondimenti li puoi trovare in WolframAlpha, cercando mathworld subject multivariate statistics.
Esistono molte altre tecniche per analizzare forme di collegamento tra dati di vario genere.
Una particolarmente usata è la cluster analysis, di cui
qui (clicca, poi,
)
Esercizi:
Vedi qui per un uso di R impiegando la libreria
19
