 Verifica della verosimiglianza delle ipotesi
Verifica della verosimiglianza delle ipotesiIn questa voce ci occuperemo di alcune (tra le molte) tecniche per prendere delle decisoni sulla base di dati statistici raccolti sperimentalmente.
 Verifica della verosimiglianza delle ipotesi
Verifica della verosimiglianza delle ipotesi
Valutata la probabilità di un evento o individuata una legge di distribuzione o … solo sulla base di dati sperimentali, non abbiamo la certezza di questa conclusione. Possiamo, comunque, porci il problema di quanto sia verosimile l'ipotesi che il valore o la funzione o … individuata sia effettivamente una buona approssimazione, cioè valutare la probabilità che il suo scarto dall'oggetto (valore, funzione, …) "vero" rientri nei margini di aleatorietà dovuta alla limitatezza del materiale statistico a disposizione. In base a questa valutazione, a seconda della situazione (con considerazioni pratiche, legate al contesto, ai rischi sociali, …), potremo stabilire se tale ipotesi è accettabile o è da rifiutare.
Abbiamo affrontato attività di questo tipo alla voce
 limiti in probabilità:
all'intervallo frequenza
limiti in probabilità:
all'intervallo frequenza
Se in base a qualche ragionamento ho ipotizzato che Pr(A) sia 3/7 e
trovo che 3/7 sta nell'intervallo frequenza
In questa voce vedremo in particolare come valutare l'attendibilità di una legge di distribuzione.
 Verifica della verosimiglianza di una legge di distribuzione.
Il test "chi quadro".
Verifica della verosimiglianza di una legge di distribuzione.
Il test "chi quadro".
Poniamoci il problema di valutare la conformità tra una distribuzione sperimentale e una teorica.
Per valutare la discordanza tra un valore sperimentale Us e un valore teorico U uso la differenza (o errore o scarto o deviazione) Us–U.
Come valutare la discordanza tra gli esiti di n prove, classificati in nc classi, e una certa legge di distribuzione?
Supponiamo di voler confrontare con la distribuzione Pr(U=2)=1/36, Pr(U=3)=2/36, … gli esiti del lancio di una coppia di dadi ripetuto n volte. Indichiamo con FrOs1, …, FrOs11 le frequenze assolute osservate (FrOs1 + FrOs11= n) e con FrAt1, …, FrAt11 le frequenze assolute attese, cioè i valori che si otterrebbero da FrequenzaAssoluta = n · FrequenzaRelativa mettendo Probabilità al posto di FrequenzaRelativa: FrAt1 = n·1/36, FrAt2 = n·2/36, ….
|
|
Una idea è prendere X =
Uno scarto da una frequenza attesa bassa, come d1, deve però essere pesato di più di uno da una frequenza attesa alta, come d2: la deformazione dall'istogramma teorico è maggiore se si è in un punto in cui il grafico è basso. Per migliorare la valutazione della difformità considero gli scarti quadratici relativi: |
| X = Σ(FrOsi−FrAti)2 / FrAti |
Nel caso di un'altra variabile casuale U le frequenze attese in ciascuna delle nc classi (intervallini o altri insiemi) Ii in cui ho classificato gli n dati saranno calcolate analogamente:
FrAti = n·pi, dove pi = Pr(U ∈ Ii), i = 1, …, nc.
Se U è continua Pr(U ∈ Ii) sarà calcolato integrando su Ii la funzione densità.
X è una variabile aleatoria (ogni volta che effettuo n prove X assume un valore casuale) che,
oltre che dal fenomeno studiato, dipende dal numero delle prove n, dalle classi I1,
…, Inc scelte e dai valori
Nel caso di fenomeni che seguano realmente la legge L, X avrà una certa distribuzione teorica. Se confronto il valore X* di X che ottengo per un particolare fenomeno con tale distribuzione teorica, posso valutarne la "normalità": se X* è anormale posso ritenere non verosimile che il fenomeno si manifesti secondo la legge L.
| Indichiamo con χ2 ("chi quadro") X o X*, a seconda dei casi, lasciando al contesto il superamento dell'ambiguità. |
|
Consideriamo ad esempio un dado di cui si sono effettuati 50 lanci ottenendo 9 uno, 11 due, 5 tre, 8 quattro, 10 cinque e 7 sei e, per valutare la discordanza dalla distribuzione uniforme (distribuzione corrispondente ai dadi equi), calcoliamo il relativo χ2. Poniamoci, poi, il problema di individuare la distribuzione χ2 teorica nel caso in cui il dado sia realmente equo, in modo da poter confrontare con essa il χ2 trovato e valutare la verosimiglianza dell'equità del nostro dado.
Potremmo svolgere il calcolo "a mano". Effettuiamolo mediante il programma R. Otteniamo 2.8.
FrOss <- c(9,11,5,8,10,7)
Prob <- c(1/6,1/6,1/6,1/6,1/6,1/6)
n <- sum(FrOss);
sum((FrOss-n*Prob)^2/(n*Prob))
2.8
Effettuato questo calcolo, che cosa possiamo concludere sulla equità del dado?
Studiamo la distribuzione teorica χ², cioè come si distribuirebbe il valore di
χ² se il dado fosse equo. Realizziamo questo studio sperimentalmente, con una simulazione dei 50 lanci.
Ecco l'esito della generazione di 10000 valori, analizzato con R:
Pro <- c(1/6,1/6,1/6,1/6,1/6,1/6); FrAt <- 50*Pro
x <- NULL; y <- NULL; for (prov in 1:1e4) {
for(i in 1:6) y[i] <- 0; for (k in 1:50)
{u <- floor(runif(1)*6+1); y[u] <- y[u]+1}
# ho preso a caso 50 uscite e l'ho classificate
x[prov] <- sum((y-FrAt)^2/FrAt) }
summary(x)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 0.160 2.800 4.480 5.014 6.640 23.920
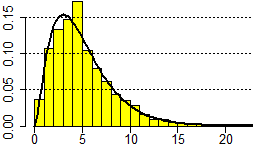
hist(x, probability=TRUE,right=FALSE,seq(0,24,1))
abline(h=c(0.05,0.1,0.15),lty=3)
|
|
Posso osservare dall'istogramma che 2.8 è un valore abbastanza centrale. Calcolando anche i percentili trovo che 2.8 è il 25° percentile, cioè il limite sinistro del 50% centrale dei dati. Quindi posso ritenere plausibile (cioè non rifiutare) l'ipotesi che il dado sia equo. Se avessi ottenuto un valore verso la coda sinistra o quella destra avrei invece dovuto avere dubbi su tale ipotesi: se è verso la coda destra si tratta di un valore molto alto, che fa supporre un dado non equo; se è verso la coda sinistra si tratta di un valore molto basso, ma un po' troppo "perfetto", che fa supporre che ci sia stato qualche errore (o qualche "imbroglio") nel riportare le frequenze. In tali casi, prima di scartare l'ipotesi, sarebbe stato opportuno, se possibile, ripetere i lanci, ricalcolare χ2 e valutare la posizione del nuovo valore rispetto all'istogramma sopra riprodotto (o rispetto ai percentili).
Nel caso di un'altra legge di distribuzione L, altre classi o un altro numero n di prove, ad esempio nel caso dell'esempio iniziale o del quesito 12, si può procedere analogamente: studiare sperimentalmente con una simulazione la distribuzione del relativo χ2 e confrontare con essa il valore calcolato di χ2.
In genere, tuttavia, si preferisce utilizzare un procedimento standard di tipo generale, che ha il seguente retroterra teorico:
si può dimostrare che, se il numero n delle prove è sufficientemente grande, la legge di distribuzione teorica di χ2 è praticamente indipendente dalla legge di distribuzione L:
|
per n tendente all'infinito tende a una legge χ2(r) che dipende solo dal numero r dei gradi di libertà, cioè dalla quantità delle frequenze sperimentali che devo conoscere direttamente. |
|
Spieghiamo meglio il concetto di "grado di libertà" con alcuni esempi.
Nel caso del dado sopra considerato, sappiamo che le frequenze FrOss1, FrOss2, …, FrOss6 devono avere come somma n: questa connessione fa sì che note 5 frequenze la rimanente sia determinata automaticamente. Questa connessione è presente in tutti i casi. Quindi i gradi di libertà sono in ogni caso al più nc−1 (nc = numero delle classi).
Nel caso di una variabile casuale a valori in (0,∞),
se FrOss1,…, FrOss16 sono le frequenze osservate nei 16 intervalli [0,5), [5,10), …
e voglio operare il confronto con la densità esponenziale
[Pr(U∈I1),
Pr(U∈I2), …
in questo caso sono gli integrali tra 0 e 5, tra 5 e 10, … della densità,
cioè F(5)–
Se, invece, come w avessi scelto un valore stabilito a priori, non dipendente dai dati sperimentali, non avrei avuto la connessione ΣxiFrOssi/n=M, e i gradi di libertà sarebbero stati 15.
---------------- L'espressione di χ²(r) non è facile da descrivere né da comprendere (non è una delle cosiddette
funzioni "elementari": vedi). Comunque nel software matematico in genere è definita
e richiamabile con degli opportuni comandi. In R la funzione densità della legge χ²(r) è calcolabile
con la funzione che ad x associa dchisq(x, r) ("sq" sta per "square"). f <- function(x) dchisq(x, 5); plot(f, 0,25, add=TRUE,lwd=2) |
 |
Se mi interessano i quantili (o percentili) della legge χ² uso, invece, qchisq(x, r). Vediamo qual è il quantile di ordine 0.25 (o 25º percentile) nel caso del dado equo: con qchisq(0.25,df=5) ottengo 2.674603. Ritrovo che 2.8 è circa il quantile di ordine 0.25 (ossia il 25º percentile).
Se, viceversa, mi interessa la funzione di distribuzione (o ripartizione), che ad x associa la probabilità che χ² sia minore di x (ovvero che ad x associa l'ordine del quantile che vale x), uso pchisq(x, r). Vediamo qual è l'ordine del quantile che nel caso del dado equo vale 2.8 con pchisq(2.8,df=5) ottengo 0.2692135. Trovo che 2.8 è il quantile di ordine 0.27 (ossia il 27º percentile): la probabilità che il χ² si minore di 2.8 è 0.27.
Confrontiamo i valori ottenuti sopra con summary(x) con quelli ottenibili con qchisq e con dchisq:
qchisq(c(0.25, 0.50, 0.75), df=5) # 2.674603 4.351460 6.625680 25°,50°,75° percentile f <- function(x) dchisq(x, 5)*x integrate(f,0,Inf) # 5 il valor medio
Ecco i valori per diversi gradi di libertà (ottenuti coi comandi riportati qui):
g.l. 5 10 25 50 75 90 95 1 0.00393 0.0158 0.102 0.455 1.32 2.71 3.84 2 0.103 0.211 0.575 1.39 2.77 4.61 5.99 3 0.352 0.584 1.21 2.37 4.11 6.25 7.81 4 0.711 1.06 1.92 3.36 5.39 7.78 9.49 5 1.15 1.61 2.67 4.35 6.63 9.24 11.1 10 3.94 4.87 6.74 9.34 12.5 16 18.3 20 10.9 12.4 15.5 19.3 23.8 28.4 31.4 50 34.8 37.7 42.9 49.3 56.3 63.2 67.5 100 77.9 82.4 90.1 99.3 109 118 124
Tornando al nostro dado (5 g.l.), se come χ² invece di 2.8 (che è intorno al 25° percentile e quindi è abbastanza "normale") avessimo ottenuto 13 avremmo dovuto manifestare qualche dubbio sul fatto che il dado sia equo: c'è una discordanza molto alta rispetto alla legge uniforme: il 95° percentile è 11.1.
Ma anche se avessimo ottenuto una discordanza molto bassa, ad esempio χ²<1, avremmo dovuto avere dei dubbi sulla equità del dado o sulla attendibilità dei dati fornitici: è improbabile che si ottenga un valore inferiore a 1 (la probabilità è inferiore al 4%, infatti pchisq(1, 5) = 0.037).
Un amico mi dice: Questa moneta è equa. Infatti su 1000 lanci ho ottenuto 499 "testa" e 501 "croce". Che cosa possiamo concludere sulla verosimiglianza di quanto raccontato dall'amico?
Trovo χ2 = (499–500)2/500+(501−500)2/500 = 2/500 = 4/1000.
[
FrOss <- c(499,501); Prob <- c(1/2,1/2); n <- sum(FrOss)
sum((FrOss-n*Prob)^2/(n*Prob))
[1] 0.004 ]
Dalla tabulazione ho che 0.004 corrisponde circa al percentile di ordine 5. Si tratta quindi di un valore piuttosto anormale. È sensato ritenere che l'amico ci abbia raccontato una frottola.
Nell'usare la distribuzione del χ² limite occorre prestare qualche attenzione: occorre che le prove siano numerose (diciamo, almeno un centinaio); occorre, inoltre, che in ogni classe (di quelle in cui le prove sono state classificate - da chi ha fornito le informazioni o direttamente da voi) cadano abbastanza valori (diciamo, almeno 5); se in qualche classe cadono poche osservazioni è opportuno unire questa classe ad un'altra.
È facile e comodo l'impiego di un apposito script: vedi.
Il "test χ2" considerato nel paragrafo precedente è un "test di adattamento": è usato per valutare l'adattamento di una certa distribuzione teorica a una serie di dati sperimentali.
Se si assume come regione di non rifiuto (o, meglio, di coerenza o conformità tra dati e teoria) il 95% centrale, cioè l'intervallo compreso tra il percentile di ordine 2.5 e il percentile di ordine 97.5, si dice anche che l'ipotesi viene testata con un livello di confidenza (o di fiducia) del 95%: è la probabilità che, se l'ipotesi fosse "vera", la regione di coerenza contenga il valore di χ2, ovvero il test dia esito positivo.
Il complemento a 1 del livello di confidenza è l'ampiezza della regione complementare, cioè della regione critica (o di incoerenza); tale ampiezza viene invece chiamata livello di significatività (in questo caso è: 1–95%=5%): è la probabilità che, se l'ipotesi fosse "vera", la regione di incoerenza contenga il valore di χ2, ovvero il test dia ("erroneamente") esito negativo.
Esistono molti altri tipi di test statistici. Vediamone solo un paio.
Nella tabella seguente sono riportati i dati di un'indagine campionaria, relativamente ad alcune regioni e al 1990, sulla distribuzione delle abitazioni secondo la superficie abitata (area espressa in metri quadrati):
|
a) si verifichi l'ipotesi: non c'è differenza significativa (5%) tra le medie delle superfici delle diverse regioni; b) si verifichi l'ipotesi: non c'è differenza significativa (5%) tra le distribuzioni relative alle diverse regioni. | ||||||||||||||||||||||||||
Quesito a. Devo verificare la plausibilità che le medie teoriche
delle superfici abitate delle tre regioni non siano diverse, cioè che due a due abbiano
differenza 0. Devo valutare se lo scarto da 0 della differenza tra le due medie sperimentali è accettabile
come "normale" con confidenza del 95%, cioè se l'intervallo di confidenza al 95% della differenza delle medie
(l'intervallo in cui al 95% cade la differenza teorica, cioè la differenza riferita alla popolazione limite)
contiene 0.
Parlando di differenza significativa si intende dire che si deve assumere 5% come livello di
significatività, cioè come ampiezza della regione di rifiuto, ossia 100%–(probabilità di confidenza).
Le medie hanno, tendenzialmente, distribuzione gaussiana. La differenza delle medie è
la media delle differenze, che sarà anch'essa, tendenzialmente, gaussiana. Devo trovare il σ di questa gaussiana.
Per determinare le medie individuo
il valore centrale degli intervalli; nel caso del primo intervallo, 50-95, cioè [50,96),
il valore centrale è 50+semiampiezza = 50+23 = 73; i valori centrali degli altri intervalli sono 103.5, 121, 166.
Considero Campania e Liguria.
Stima della superficie abitata in Liguria: ML = (130·73+11·103.5+…)/(130+ 11+…) =
12184.5/152 = 80.16. Analogamente MC = 102.84=103, MS = 92.85.
La differenza tra le due medie sperimentali è 22.68.
La varianza della differenza è la somma delle varianze; le varianze delle
due medie (calcolate a mano o con STAT, una calcolatrice o un foglio di calcolo) sono 2.593 e 0.147; quindi
σ =
Al 95.4% (significatività del 4.6%) il valore dovrebbe cadere in [m–2σ, m+2σ] = [0–1.66·2, 0+1.66·2] = [–3.32, 3.32], che non contiene 22.68. A maggior ragione l'ipotesi è da rifiutare al livello di significatività del 5% (per avere una confidenza al 95% occorre prendere, invece di 2·σ, t·σ con t = 1.96; l'intervallo di confidenza diventa [1.66·1.96, 1.66·1.96] = [–3.25, 3.25]).
Quesito b. La richiesta equivale al fatto che le tre distribuzioni siano tendenzialmente proporzionali, cioè al fatto che la modalità "regione" sia indipendente dalla modalità "superficie".
Dobbiamo quindi confrontare le frequenze sperimentali nelle 12 celle della tabella – la cella incrocio della riga "Liguria" e della colonna [50,96), …, quella incrocio di "Sicilia" e [131,200) – con le frequenze attese – i prodotti (frequenza di "Liguria")·(frequenza di [50,96)), …, (frequenza di "Sicilia")·(frequenza di [131,200)). Si fa ciò usando il test χ2. Si ottiene χ2=1342.
I gradi di libertà sono (4–1)·(3-1) = 6; infatti fissate le frequenze totali delle 4 regioni e delle 3 classi di appartamento (sono i valori che uso per calcolare le frequenze attese), di ogni riga mi basta conoscere 3 celle (la quarta la ottengo usando la frequenza totale della riga) e, analogamente, di ogni colonna 3–1=2 celle. Dalla tabulazione di χ2 si ottiene la non normalità (al 95%) di questo valore: l'intervallo di normalità al 95% dovrebbe essere quello compreso tra i percentili di ordine 2.5 e 97.5, cioè:
round(qchisq(c(2.5, 97.5)/100, df=6),2) [1] 1.24 14.45
Questi sono tipici esempi in cui a occhio, guardando le tabelle, si vede che le ipotesi considerate sono sicuramente da rifiutare. I valori molto grandi di χ2 confermano bene ciò. Sono esempi in cui non è molto "sensato" porsi il problema di usare il test χ2. Li abbiamo fatti solo per esemplificare i test.
• Accanto al concetto di livello di confidenza di un test,
richiamato sopra, cioè la probabilità
Accanto al rischio di commettere un cosiddetto errore di tipo I, ossia di ottenere erroneamente esito
negativo (livello di significatività, o α-rischio, già
discusso), si considera anche il rischio di commettere un errore di tipo II, ossia di ottenere erroneamente
esito positivo (β-rischio).
• A volte si usa il test χ2 non in modo "bilaterale" come si è fatto qui, cioè rifiutando, come anormali, anche le ipotesi che danno luogo a valori di χ2 "piccoli", ma in modo "unilaterale", rifiutando solo i casi in cui si ottengono χ2 "alti" (ad es. a una significatività del 5% corrisponde un ordine di percentile non tra 2.5 e 97.5 ma sotto a 5).
• Testare un'ipotesi H di diseguaglianza, come "k ≤ M(X)",
è più complicato che testarne una di eguaglianza, come
Se H è k ≤ M(X), con testare H con il livello di significatività
p% si intende: prendere M(X)=k come H0 e
Esempio.
(1) Ho 20 dati
(10.4, 9.3, 11.2, 10.1, 10.8, 9.7, 9.7, 8.2, 10.2, 10.6, 9.5, 10.0, 10.1, 10.2, 10.3, 9.2, 10.4, 8.8, 11.0, 8.7)
relativi alla concentrazione X (grammi/litro) di un sale in una soluzione. Assumo che X sia distribuita gaussianamente.
Voglio testare l'ipotesi che
Per trovare intervalli di confidenza della media, come si è visto, si usa il fatto che Mn(X) ha andamento gaussiano. Per trovare intervalli di confidenza per la varianza di una distribuzione gasussiana di s.q.m. σ si utilizza il fatto (che non dimostraiamo) che la variabile statistica Varn(X)·n/σ ha distribuzione χ2(n–1).
Coi miei dati ottengo 9.71 come V20(X)·20/(1.1)2, cioè come χ2(19) sperimentale. I percentili di ordine 2.5 e 97.5 sono 8.9 e 32.9; 9.71 sta quindi nella regione di coerenza.
(2) Se invece voglio testare l'ipotesi che
(3) Se invece voglio testare l'ipotesi che
Quindi sia l'ipotesi
• Accenniamo, infine, per dare un'idea della complessità
dell'argomento, ad alcuni impiego del test t di Student, il
cui uso abbiamo già citato nel caso univariato
 limiti
limiti
tr <- c(339, 405, 302, 362)
co <- c(401, 340, 461, 442, 361)
t.test(co,tr, var.equal=TRUE)
# Two Sample t-test
# t = 1.5193, df = 7
# mean of x mean of y
# 401 352
## Ho ottenuto l'indice t di Student 1.52. I gradi di libertà (df) sono 7 (3+4)
## La significatività si controlla, in modo analogo al test χ², ricorrendo
## alla densità dtS della distribuzione t
g <- 7; dtS <- function(x) dt(x,df=g)
plot(dtS,-5,5)
abline(h=axTicks(2),v=axTicks(1),lty=3)
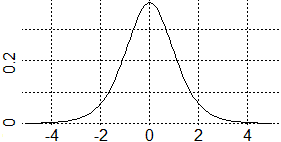
## Determino x tale che l'integrale tra -x ed x sia 0.95 (ma potrei scegliere
## 0.99 o 0.9 o …, a seconda delle esigenze).
idtS <- function(x) integrate(dtS,-x,x)$value-0.95
uniroot( idtS,c(0,100))$root
# 2.364625
## Il valore di t al 95º percentile è 2.365
## 1.52 è inferiore a 2.365. Non è una differenza significativa: è azzardato
## affermare che il preparato diminuisca la respirazione delle cellule epatiche
Vediamo anche il confronto delle medie di una coppia di dati appaiati: ad un gruppo di persone viene somministrato
un presunto antitermico e vengono confontate le loro temperature al momento della somministrazione (A) e dopo tre ore (B).
Si vuole vedere se la riduzione della temperatura è significativamente diversa da zero.
A <- c(38.3, 39.1, 40.2, 37.6, 38.9, 38.7)
B <- c(37.2, 38.4, 38.6, 36.7, 38.2, 38.2)
t.test(A,B, paired=TRUE)
# Paired t-test
# t = 5.7279, df = 5
## Ho ottenuto l'indice t di Student 5.73. I gradi di libertà (df) sono 5
## Determino x tale che l'integrale tra -x ed x sia 95%
g <- 5; dtS <- function(x) dt(x,df=g)
idtS <- function(x) integrate(dtS,-x,x)$value-0.95
uniroot( idtS,c(0,100))$root
# 2.570582
## Determino anche x tale che l'integrale tra -x ed x sia 99%
idtS <- function(x) integrate(dtS,-x,x)$value-0.99
uniroot( idtS,c(0,100))$root
# 4.032137
## 5.73 è maggiore di 2.57 ed anche di 4.03. È una differenza
## significativa. Posso ritenere efficace il preparato antitermico.
Un ultimo esempio (tratto da un manuale di Prodi - Metodi matematici e statistici, McGraw-Hill, 1992).
Si può dimostrare che se X1,…,XN
sono N misure indipendenti distribuite normalmente, Mc è la media del campione, Mt la media del totale della popolazione
e σ è la deviazione standard campionaria, allora t = (Mc−Mt)/σ·√N segue una
legge di Student (a N-1 gradi di libertà). Ipotizziamo che un certa grandezza G abbia, rispetto ad una certa unità
di misura, il valore 2.4. Si effettuano 10 misure ottenendo media Mc=2.7 e σ=0.3. Ammettiamo che gli errori di misura
abbiano una distribuzione normale (di parametri ignoti). L'ipotesi su G deve essere accettata o rifiutata, se assumo un livello
di significatività di 0.05?
# 1-0.05 = 0.95
idtS <- function(x) integrate(dtS,-x,x)$value-0.95
uniroot( idtS,c(0,100))$root
# 2.262158 (il valore di t al 95º percentile)
## La variabile di Student nel nostro caso ha il valore:
(2.7-2.4)/0.3*sqrt(10)
# 3.162278
## Devo respingere la teoria. Ma se avessi assunto un livello di
## significatività dello 0.01 la avrei accettata:
idtS <- function(x) integrate(dtS,-x,x)$value-0.99
uniroot( idtS,c(0,100))$root
# 3.249836 (> 3.162278)
Per approfondimenti vedi l'help di R (batti "help(t.test)" e "help(dt)")
o WolframAlpha (batti "student's t distribution") o
WikiPedia (versione inglese).
Un altro test usato spesso nel caso continuo è quello di Kolmogorov-Smirnov
(batti in R "help(ks.test)" o in WolframAlpha "kolmogorov-smirnov test").