Concavità di una funzione

  Richiami sui punti di massimo e minimo

L'immagine seguente sintetizza quanto visto (alla voce  derivata) sui legami tra la derivata di una funzione (qui indicata con  f ) e la collocazione dei suoi punti di massimo e di minimo.

( clicca l'immagine se vuoi ingrandirla )

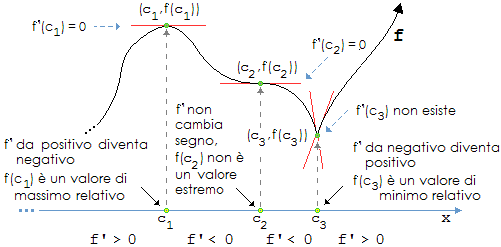
    I punti c in cui D(f) si annulla (in essi f può avere un massimo o un minimo relativo, ma non è detto che ciò accada, come nel caso di c₂) vengono detti punti critici ed f viene detta stazionaria in essi (o essi vengono detti punti stazionari).
    In situazioni in cui sia facile studiare le derivate successive di una funzione può essere utile ricorrere all'analisi di queste per studiare la collocazione dei punti di massimo e di minimo. Per affrontare questo argomento è bene mettere prima a punto il concetto di concavità di una funzione.

  Concavità di una funzione

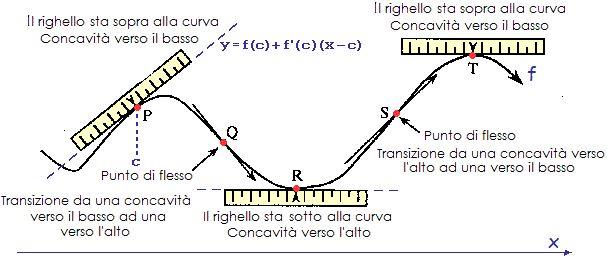
L'immagine seguente richiama il significato intuitivo del concetto di concavità, che poi andremo a precisare.

( clicca l'immagine se vuoi ingrandirla )

Generalizzando il significato di concavità già introdotto per i poligoni ( triangoli) diciamo che il grafico di una funzione continua ha la concavità verso il basso attorno al punto (c, f(c)) se  – vedi figura precedente –  attorno ad esso (ossia per valori della ascissa che stanno in un intervallo che ha al suo interno c) il grafico di f sta al di sotto o coincide con una retta passante per tale punto. Se la funzione è derivabile, ciò accade se il grafico di f sta al di sotto o coincide con la retta tangente alla curva in tale punto, ossia se, per x abbastanza vicino a c,  f(x) ≤ f(c) + D(f)(c) (x−c).

Analogamente, f ha la concavità verso l'alto attorno a un punto  – come il punto R nella figura precedente –  se il grafico di f sta al di sopra o coincide con una retta passante per tale punto; ossia, se c è la ascissa di esso e la funzione è derivabile, se, per x abbastanza vicino a c,  f(x) ≥ f(c) + D(f)(c) (x−c).     Se aggiungiamo l'avverbio "strettamente" ("… è strettamente concava …") intendiamo che la funzione intorno a c non può avere andamento rettilineo (ovvero il suo grafico può coincidere con quello della retta considerata solo nel punto di ascissa c).     Si usano, per f, anche i termini "concava" e "convessa" (al posto di concava verso il basso e verso l'alto), come richiamato dalla figura a lato, pensando alle forma della figura che, intorno al punto considerato, sta al di sopra del grafico di f ( triangoli).     Si noti che la somma di due funzioni con la concavità verso l'alto (verso il basso) è una funzione con la concavità verso l'alto (verso il basso).

A sinistra il grafico di una funzione che in 0 ha la concavità verso l'alto senza essere ivi derivabile. Esercizio:  testo e soluzione

  Concavità e derivata seconda

È intuitivo che  se una funzione f ammette derivata seconda f " in c allora il grafico di f è strettamente concavo verso l'alto in (c, f(c)) se f "(c) > 0  e che  il grafico di f è strettamente concavo verso il basso in (c, f(c)) se f "(c) < 0.  Basti pensare al fatto che il segno della derivata seconda, f ", esprime la crescita o la decrescita della pendenza di f.  Del resto ( funzione 2) la derivata seconda di una funzione che ha per grafico una parabola ha lo stesso segno del coefficiente direttivo, che determina se la concavità della parabola è all'insù o all'ingiù.

Per un altro esempio si pensi a f: x → x3 − 3x2 + x − 2 (vedi il grafico a lato; cliccalo se vuoi vederlo più grande). Determiniamo dove il grafico ha la concavità verso l'alto e dove verso il basso. Poiché la funzione è facilmente derivabile due volte, possiamo usare quanto osservato sopra: f″(x) = 6(x − 1), dunque  f″(x) > 0 se x > 1 e f″(x) < 0 se x < 1,  e, quindi, f ha grafico con concavità verso l'alto nei punti di ascissa maggiore di 1 e concavità verso il basso in quelli con ascissa minore di 1.

Nell'esempio sopra rappresentato graficamente, la concavità del grafico cambia per l'input uguale a 1: il corrispondente punto del grafico viene detto punto di flesso. Più in generale ho che  se D(f) esiste (tranne eventualmente che in c) e f " ha segni diversi a sinistra e a destra di c,  allora (c, f(c)) è un punto di flesso, e se f "(c) esiste allora f "(c) = 0.

Nel caso precedente abbiamo che f '(x) = 3x² − 6x + 1 = 0  per x = 1 − 2√6/6  e per x = 1 + 2√6/6, e che in tali punti f (di cui sopra abbiamo visto il grafico) ha un massimo e un minimo relativi. Ma avremmo potuto concludere qual è il massimo e quale il minimo studiando il segno di f ":
se f '(c) = 0, f ' esiste in un intorno di c e f "(c) esiste, allora f ha un massimo relativo in c se f "(c) < 0, un minimo relativo se f "(c) > 0, non si può concludere nulla se f "(c) = 0.

Evitiamo, qui, di provare queste proprietà, di cui è facile convincersi, ma che non sono di banale dimostrazione.

Qui,  qui  e  qui  trovi come svolgere questi calcoli con R, e alcune animazioni.

Per approfondimenti su quanto è liscia (smooth) una funzione (ovvero il suo grafico) vedi qui.

Nota.  Per indicare la derivata seconda di f, oltre che a f " si usano anche f⁽²⁾ e D²(f).

Esercizi:   testo e soluzione,   testo e soluzione

 altri collegamenti     [nuova pagina]