Curve approssimanti

    Come si può cercare di approssimare un grafico sperimentale (il grafico della relazione tra due grandezze, un istogramma di distribuzione frutto di un rilevamento statistico, ...) con una curva "bella" (cioè che si può descrivere facilmente mediante funzioni elementari)?

    Innanzi tutto facciamo qualche chiarimento terminologico, a partire da un esempio.

  Interpolazione e approssimazione

    Supponiamo di avere le 5 informazioni rappresentate sotto nella figura A relativamente a come un fenomeno y varia in funzione del fenomeno x.  Per stimare i valori assunti da y per i valori di x intermedi possiamo approssimare l'intero fenomeno congiungendo i punti con segmenti (figura B). Questa tecnica si chiama interpolazione lineare: si ottiene una funzione (continua lineare a tratti) che nei 5 punti noti coincide con la nostra y in funzione di x; la possiamo usare per approssimare y per gli altri valori di x.  Volendo ottenere una curva "totalmente liscia" (continua con tutte le sue derivate) potremmo individuare la funzione polinomiale di grado minimo che passa per tutti i 5 punti (figura C); ma questa interpolazione polinomiale in genere dà luogo a cattive approssimazioni.  Un'ulteriore possibilità è approssimare l'andamento tra i vari dati rilevati con diverse funzioni polinomiali tali da garantire che la curva risultante sia abbastanza liscia (interpolazione con spline): ad esempio con funzioni polinomiali di 2° grado, imponendo che la funzione risultante sia derivabile anche nei 5 punti (e un'ulteriore condizione, ad es. che il primo tratto sia rettilineo) o di 3° grado, imponendo che essa sia derivabile fino al 2° ordine, e che le derivate seconde nel primo e nell'ultimo punto siano nulle (figura D).

    Sotto sono rappresentati graficamente gli esiti di 12 rilevamenti della portata d'acqua in m³/s (asse verticale) di un fiume italiano effettuati nel corso di un anno, a distanza di circa 30 giorni (asse orizzontale) l'uno dall'altro.   Per stimare la portata negli altri giorni l'intero fenomeno è stato approssimato (al centro) con una interpolazione lieneare e (a destra) con una spline cubica.

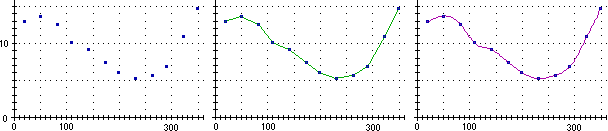
    Qui e qui trovi esempi di tracciamenti di spline cubiche con R.

Esercizi

    Non si parla, invece, di interpolazione, ma solo di approssimazione, se si vuole trovare una funzione il cui grafico passi vicino ai vari punti noti, senza necessariamente passare per essi. Questo è ciò che si farebbe se si volessero individuare delle regolarità nel fenomeno e si cercasse di descriverlo in modo sintetico, o se (ma non è questo il caso) si trattasse di rilevamenti ad alta sensibilità, soggetti a errori casuali non stimabili a priori, per cui non avrebbe senso porsi il problema di trovare curve che passino esattamente per i punti sperimentali.

    Si parla di estrapolazione quando si cerca di prolungare un'interpolazione a sinistra (oltre il primo dato) o a destra (oltre l'ultimo).

    In inglese si parla di curve fitting per indicare la costuzione di una curva che approssimi o interpoli dei punti sperimentali (la curva che abbia "the best fit", il migliore adattamento, secondo i criteri stabiliti).

    Noi ci occuperemo in particolare di alcune tecniche generali di approssimazione.

  Uso di scale semilogaritmiche, bilogaritmiche, quadratiche e cubiche.
     Calcolo e rappresentazione delle pendenze

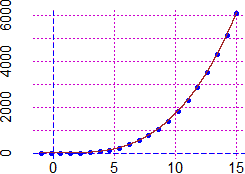
Nel file  bilog.htm  sono contenute delle coppie (x,y) ottenute tabulando una funzione polinomiale, sotto a sinistra rappresentate graficamente.     Per capire di quale grado è il polinomio possiamo rappresentare i dati su carta bilogaritimica come quella raffigurata a fianco, ossia in cui sull'asse orizzontale e su quello verticale sono usate delle scale logaritmiche  ( funzione esponenziale).     Ovvero possiamo trasformare i dati applicando il logaritmo sia alle x che alle y (dopo aver traslato i dati in modo da renderli positivi: figura sotto a destra) e rappresentare i nuovi dati in un usuale sistema di riferimento, come nella figura a sinistra nella riga successiva, e osservare che tendono a disporsi lungo una retta.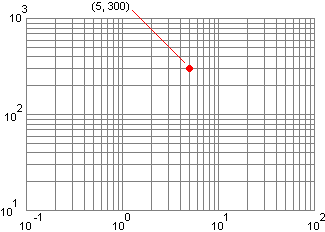

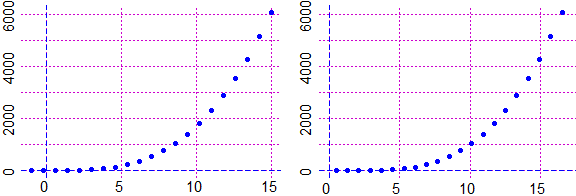
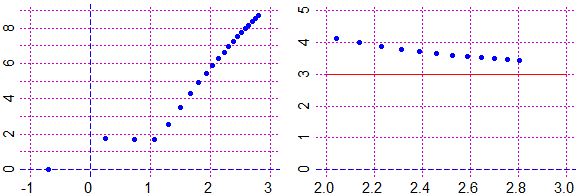
Infatti y = axn+bxn–1+… per x → ∞ tende a comportarsi come y = axn, che è trasformata in  Y = log(y) = log(a)+n·log(x) = log(a) + n·X:  il grafico trasformato tende a disporsi lungo una retta di pendenza n.  In questo caso posso ricavare usando le informazioni sulla scala che n  (che so essere intero)  deve essere 3.  Osservo meglio la cosa facendo il grafico delle pendenze dei segmenti che costituiscono il grafico (vedi la figura sopra a destra).  Capito che la funzione polinomiale č di terzo grado, posso poi trovarne l'equazione con tecniche chiamate "di regressione", che vengono discusse in una voce successiva, e verificare graficamente la corrispondenza (figura qui a destra).     Qui puoi vedere come realizzare tutto ciò con R.

  Il metodo precedente ha successo se i dati hanno andamento polinomiale. Se supponiamo che i dati abbiano andamento esponenziale, come quelli nel file semilog.txt, rappresentato graficamente sotto a sinistra, possiamo usare una carta semilogaritmica, ovvero con scala logaritmica solo sull'asse y, o, in altri termini, usando Y = log(y). Infatti una curva esponenziale così trasformata diventa una retta:
y = a e^{b x}  →  Y = log(y) = log(a)+ x b.
    Ecco, a destra, la trasformazione del grafico precedente ottenuta in tal modo. Cerchiamo di trovare a e b.
    È stata tracciata una retta approssimante. Essa ha equazione Y = –0.1*x–2.35.
Ho b ≈ –0.1.  Da  log(a) = –2.35  deduco che:
      a ≈ e^–2.35 ≈ 0.09536916 ≈ 0.1.

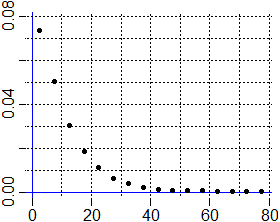
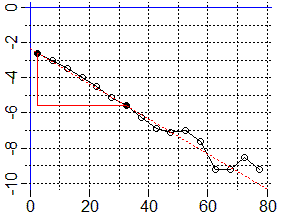
    Qui puoi vedere come realizzare tutto ciò con R (con una stima migliore di y = 0.1·exp(−1).

  I dati ad andamento polinomiale studiati sopra con una trasformazione bilogaritmica possono essere studiati anche attraverso successivi passaggi al grafico della pendenza.  Se si impiegano n passaggi per arrivare a punti con andamento approssimativamente rettilineo, ciò significa che i dati avevano approssimativamente andamento polinomiale di grado n+1. Ecco la rappresentazione grafica di alcuni dati e quelle delle successive pendenze:

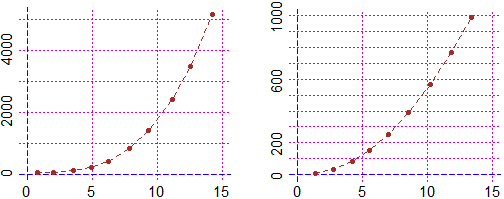
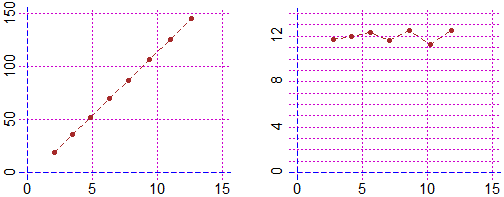
    Con 2 passaggi alla pendenza si è arrivati a un andamento (quasi) lineare; quindi la funzione tabulata era approssimativamente un polinomio di grado 3.  Dal fatto che l'ultimo grafico è, circa, la retta di ordinata 12 deduco che il coefficiente direttivo del polinomio è, con buona approssimazione, 12/3/2 = 2.  Qui puoi vedere come realizzare tutto ciò (e approfondire lo studio) con R.

  Se si fossero rappresentate le successive pendenze di un file di dati ad andamento esponenziale si sarebbero sempre ottenuti grafici crescenti (la derivata di una funzione esponenziale è ancora una funzione esponenziale).
    Nel caso di dati con andamento del tipo x → xⁿ √x = x^n+1/2 si sarebbe passati dalla pendenza di ordine n crescente a quella di ordine n+1 decrescente.

A destra, si può osservare la rappresentazione del nostro file ad andamento polinomiale di terzo grado trasformato con  x' = x, y' = y1/3 = 3√y.     In pratica, è una rappresentazione con scala verticale cubica.  Il grafico di una funzione polinomiale di grado 3 viene trasformato in un grafico che tende a disporsi lungo una retta avente come pendenza la radice cubica del coefficiente direttivo. Dal grafico o, meglio, facendo il grafico della pendenza di questo nuovo grafico, si ottiene che la radice cubica del coefficiente direttivo è 1.26, da cui si ha che il coefficiente direttivo è 2.00, in accordo con quanto trovato con l'altro metodo.

  Medie Mobili

Una tecnica molto impiegata per approssimare dati è costituita dall'uso delle medie mobili (di ordine 3), in particolare per analizzare serie storiche. Essa consiste nel sostituire ogni punto con quello avente comme coordinate le medie delle coordinate sue e dei punti ad esso precedente e seguente (il punto inziale e quello finale non vengono modificati, o vengono eliminati nella nuova rappresentazione). Ecco l'impiego di questa tecnica per analizzare i dati relativi alle piogge a Genova contenuti nel file pioggia.txt e, in particolare, per individuare i fattori stagionali:

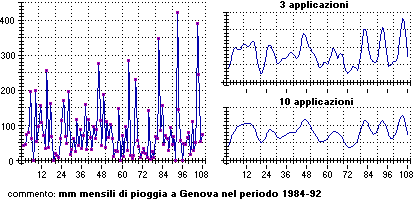[clicca l'immagine   per ingrandirla]

    Qui trovi esempi di tracciamenti di medie mobili con R.   Qui trovi uno script per studiarle facilmente online.

  Uso di un foglio di calcolo

Le tecniche viste possono essere in parte anche applicate ricorrendo a un foglio di calcolo.  Ecco ad es. come usarne uno per analizzare i dati (1,2.25), (2,19.3), (3,65.2), (4,149), (5,302), (6,515), (7,820) con il metodo della pendenza. In questo caso Δx è sempre 1, per cui invece che calcolare pendenze successive mi posso limitare a calcolare delle differenze successive:

- riproduco a destra la "formula" della cella B2 (automaticamente vengono modificati i riferimenti alle celle); - riproduco la riga in basso più volte, saltando la prima cella.     Dall'analisi della tabella, tenendo conto che i dati non sono esatti e che gli errori di approssimazione facendo le sottrazioni aumentano  (ad es. se su 149, 302, 515 e 820 l'errore fosse 5, sulle differenze prime sarebbe 10 e sulle terze sarebbe 20),  posso ritenere che le differenze terze siano in crescita e che le quarte si siano stabilizzate.     Ne deduco la approssimabilità con un polinomio di 3° grado.

A B C D E F G 1 2.25 19.3 65.2 149 302 515 820 2   =B1-A1             A B C D E F G 1 2.25 19.3 65.2 149 302 515 820 2   =B1-A1 =C1-B1 =D1-C1 =E1-D1 =F1-E1 =G1-F1 3                 A B C D E F G 1 2.25 19.3 65.2 149 302 515 820 2   =B1-A1 =C1-B1 =D1-C1 =E1-D1 =F1-E1 =G1-F1 3     =C2-B2 =D2-C2 =E2-D2 =F2-E2 =G2-F2 4       =D3-C3 =E3-D3 =F3-E3 =G3-F3     A B C D E F G 1 2.25 19.3 65.2 149 302 515 820 2   17.05 45.9 83.3 153 213 305 3     28.85 37.9 69.2 60 92 4       9.05 31.3 -9.2 32

    Il foglio di calcolo, comunque, è uno strumento non molto agile e flessibile, adatto solo per affrontare alcune particolari attività.

  Il metodo dei rapporti

Nel caso in cui si sia in grado di calcolare i valori di una funzione e si voglia capirne l'andamento, si può ricorre alla tecnica dei rapporti: se F(x), per x che tende all'infinito, tende all'infinito  [a 0]  come xⁿ, allora all'aumentare di x il rapporto F(kx)/F(x)  [F(x)/F(kx)]  tende ad assumere il valore kⁿ  (nel caso dell' es. precedente si può osservare che il rapporto tra i valori assunti per x=2 e x=1, quello per x=4 e x=2, quello per x=6 e x=3 sono circa 8:  al moltiplicare per 2 di x il valore della funzione tende a moltiplicarsi per 2³).
    Questo metodo è molto comodo anche per studiare sperimentalmente ordini di infinito/infinitesimo ( infiniti e infinitesimi). Se si conosce l'espressione di F(x), si può usare un programma (come R) per definire, ad es., G(x) <- function(x) F(2*x)/F(x) [o F(2*x)/F(x)] e studiare G mediante una tabulazione o una rappresentazione grafica. Lo studio è realizzabile anche con una semplice calcolatrice.

  Dati dotati di precisione

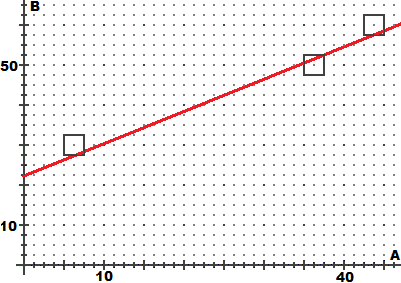
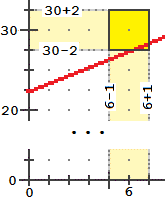
B dipende da A secondo la relazione B = 21.8 + 0.80·A, rappresentata graficamente mediante una retta nella figura sottostante a sinistra. •  Supponiamo di sapere solo che la relazione è del tipo: B = h + k A e di disporre delle seguenti informazioni, ricavate sperimentalmente: per A = 6 ± 1  B = 30 ± 2,  per A = 36 ± 1  B = 50 ± 2,  per A = 44 ± 1  B = 60 ± 2.     Ciascuna di queste informazioni sulla figura in basso a sinistra è rappresentata con un rettangolino, come si vede meglio nell'ingrandimento qui a destra: i lati orizzontali corrispondono all'intervallo di indeterminazione per A, i lati verticali a quello per B.     I potenziali grafici di B in funzione di A che sono in accordo con queste informazioni sono le infinite rette che passano per tutti e tre i rettangolini. Nella figura in basso al centro sono rappresentate, tra queste, quella di minima pendenza  (che in questo caso passa per il vertice basso destro dell'ultimo rettangolino e quello alto sinistro del primo)  e quella di massima pendenza  (che passa per il vertice alto sinistro del secondo rettangolino e quello basso destro del primo). Qui come realizzare queste rappresentazioni grafiche con R.

   
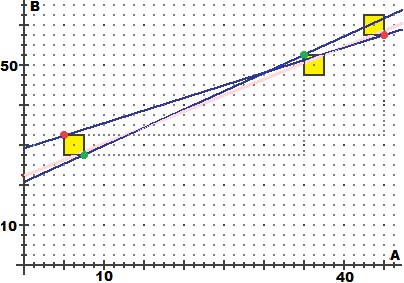
[clicca le immagini per ingrandire]

    Se mi interessasse solo conoscere il valore di k  (ossia del fattore di proporzionalità tra la variazione di A e la variazione di B)  potrei concludere che esso sta tra queste due pendenze, ossia tra (58-32)/(45-5) = 0.65 e (52-28)/(35-7) = 0.8571…, e quindi concludere:  0.65 ≤ k < 0.86
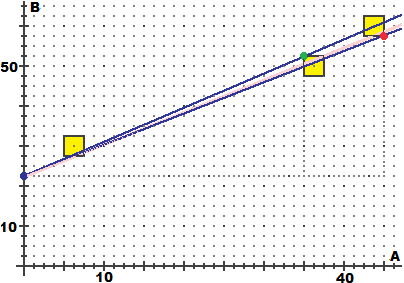
•  Se sapessi anche che h = 21.8 i potenziali grafici di B in funzione di A dovrebbero passare, oltre che per i tre rettangolini, anche per il punto di ordinata 21.8 dell'asse verticale:  vedi figura sopra a destra.  In questo caso, con un ragionamento analogo, potrei concludere che k sta tra  (58-21.8)/54 = 0.8044… e  (52-21.8)/35 = 0.8628…, e quindi:  0.80 < k < 0.87

    Qui abbiamo studiato l'individuazione dei parametri di una funzione lineare che si adatti ad alcuni dati sperimentali. Il problema può essere esteso ad altri tipi di funzioni. A questi aspetti accenneremo in una voce successiva.

    Esercizi (ulteriori rispetto a quelli presenti nel testo)

uno sol.    due sol.    tre sol.    quattro sol.    cinque sol.    sei sol.    sette sol.

 altri collegamenti     [nuova pagina]