Definizioni e dimostrazioni
Che cosa è una poesia?
Se ne cerchiamo il significato in un vocabolario possiamo trovare "componimento in versi".
Se, per capire, cercassimo anche il significato di verso potremmo trovare "ciascuna delle unità fondamentali di una composizione poetica".
In pratica una definizione rimanda all'altra e da esse non riusciamo a capire che cosa sia una poesia.
Per capire che cosa sia una poesia occorre aver letto poesie e aver imparato a chiamarle in quel modo.
Se proviamo con bicchiere possiamo trovare "piccolo recipiente usato per portare le bevande alla bocca".
In questo caso, andando a cercare recipiente, bevanda, … non incontreremo di nuovo la parola bicchiere, ma troveremo altre parole nuove, di cui a loro volta potremmo andare a cercare il significato sul vocabolario.
In ogni caso, prima a poi, arriveremmo a parole di cui il vocabolario non ci riesce a spiegare il significato:
dobbiamo apprenderlo mediante qualche figura, qualche esempio o qualche esperienza di tipo fisico o sociale.
Poi, non è detto che si concordi tutti sul significato di una parola.
Ad esempio di fronte a un certo componimento che qualcuno considera una "poesia" ci può essere chi
non è d'accordo a considerarlo tale.
Non è raro che un processo dimostri la colpevolezza di un imputato e che, dopo qualche tempo, si venga a scoprire che il colpevole era invece un'altra persona.
Oppure che due successivi processi, a partire dalle stesse "prove", diano uno una sentenza di colpevolezza e l'altro di innocenza.
In matematica definizioni e dimostrazioni vengono intese con una accezione più ristretta.
In questa voce degli Oggetti Matematici faremo qualche riflessione e precisazione a proposito delle definizioni e dimostrazioni dei matematici.
Qualche osservazione l'abbiamo già fatta in voci precedenti, ad esempio discutendo del significato di
spazio ed
eguaglianza o della validità del
teorema di Pitagora.
Esempi più elementari di dimostrazioni si possono trovare negli esercizi (vedi ad esempio gli esercizi 0a.18, 0b.4 e
1a.18 della sezione "lo spazio a 1 e 2 dimensioni" e gli esercizi 3.9, 3.11 e 3.15 della sezione "i numeri").
Modelli matematici
La differenza essenziale tra gli usi comuni di definizioni e dimostrazioni e quello matematico risiede nel fatto che la matematica è una disciplina i cui concetti e metodi vengono impiegati per affrontare problemi della più varia natura.
Quando studiamo la relazione tra due o più grandezze rappresentata sotto forma di equazione o l'andamento di un fenomeno dopo averlo descritto mediante una funzione,
lavoriamo sugli oggetti matematici (risolviamo l'equazione con tecniche numeriche o simboliche,
tracciamo il grafico usando una tabulazione e aiutandoci con il calcolo di limiti e derivate) procedendo allo stesso modo
in cui lo faremmo se le grandezze o i fenomeni considerati fossero di natura diversa.
I concetti e i metodi matematici hanno questa duttilità di impiego
perché li abbiamo introdotti e ne abbiamo studiato le proprietà in astratto, non con linguaggi e argomentazioni
che valgono solo per qualche particolare contesto.
Quindi una definizione non deve essere ambigua e una dimostrazione non può essere solo un discorso o un esperimento che ci faccia considerare molto probabile la proprietà di cui si argomenta.
Le definzioni e le dimostrazioni vengono poi, via via, riviste, generalizzate o semplificate, non solo con finalità estetiche ma per scoprirne ed estenderne l'applicabilità a nuovi contesti.
La potenza applicativa della matematica risiede nella sua astrattezza e nella "controllabilità" delle sue argomentazioni.
A questo avevamo già accennato all'inizio degli Oggetti Matematici, alla voce 
modello.
Definizioni
• Molte definizioni matematiche introducono un concetto descrivendo come ottenerlo a partire da altri.
Ad es. le potenze ad esponente intero vengono definite riconducendole a moltiplicazioni e divisioni.
Non sempre la cosa è così facile. Ad esempio nel caso delle funzioni,
prima, alla voce funzione 1, le abbiamo
descritte intuitivamente come "macchine" che a un input numerico (o più input numerici) associano un output numerico
(o più output numerici),
poi, alla voce funzione 2, come un insieme
di coppie di oggetti matematici. Ci siamo appoggiati ai concetti intuitivi di "insieme" e di "coppia", intesa come una
sequenza di due elementi.
Il concetto di sequenza è alla base di tutta la matematica e di ogni linguaggio (un numero come sequenza di cifre, una parola come sequenza di lettere, …) e non crea alcuna ambiguità.
Qualche problema in più lo può creare il concetto di insieme;
i matematici, all'inizio del XX secolo, ne hanno dato diverse definizioni che lo caratterizzano in modo
più preciso, ma le definizioni proposte non sono tutte equivalenti. La discussione di come definire il concetto di insieme è affrontabile solo in studi universitari avanzati; qui ci accontentiamo di un uso intuitivo, preoccupandoci solo di descrivere ogni nuovo insieme specificando in termini non ambigui il modo in cui generarne gli elementi o in cui verificare se un oggetto appartiene ad esso o no, e a precisare per esso una eventuale nuova nozione di eguaglianza [ strutture num. e non].
• In molti casi, definendo una nuova categoria di oggetti matematici mediante un processo di costruzione a partire da altri già definiti,
occorre precisare quando due dei nuovi oggetti sono da considerare uguali.
Ad es. abbiamo visto che espressioni come 2.4999… e 2.5000…, pur essendo diverse "come sequenze" di simboli, sono da considerare uguali "come numeri".
• Un altro modo di definire un concetto matematico è quello di elencare le proprietà che un oggetto matematico
deve avere per rientrare in tale nozione. Ad esempio questo accade quando dico che un triangolo equilatero è una figura che • è un triangolo e • ha tutti i lati uguali.
Anche il concetto di probabilità viene definito in questo modo. Possiamo scegliere diverse misure di probabilità per una stessa situazione, a patto di non entrare in contraddizione con le proprietà considerate nella definizione.
Se E è l'esito della partita Juve-Inter che si gioca domani, sia:
(a) Pr(E=1)=30%, Pr(E=2)=30%, Pr(E=X)=40% che:
(b) Pr(E=1)=70%, Pr(E=2)=10%, Pr(E=X)=20%
sono accettabili come "misure di probabilità", mentre
(c) Pr(E=1)=80%, Pr(E=2)=10%, Pr(E=X)=15% non lo è:
dovrebbe essere Pr(NOT(E=1)) = Pr(E=2 OR E=X), ma per il primo termine usando Pr(NOT A) = 100%–Pr(A) otteniamo 20%
mentre per il secondo, usando la proprietà additiva, otteniamo 25%.
Per fare un altro esempio, se definiamo gruppo una struttura che rispetto a una fissata operazione a due argomenti soddisfa la proprietà associativa, ammette un elemento neutro e per ogni elemento ha il suo inverso
[ strutture numeriche e non], possiamo dire
che, ad es., l'insieme dei numeri rispetto a "+", l'insieme dei vettori rispetto a "+", l'insieme dei numeri diversi da 0 rispetto a "·" sono gruppi.
Le proprietà che caratterizzano il concetto, quando sono esplicitamente elencate, vengono spesso chiamate assiomi. Negli ultimi esempi richiamati abbiamo considerato gli assiomi di misura di probabilità e gli assiomi di gruppo.
In precedenti voci abbiamo considerato anche altri assiomi, ad esempio quelli di distanza.
• Abbiamo anche visto come, scegliendo diversamente gli oggetti che soddisfano gli assiomi,
si possono ottenere sviluppi diversi anche di altri concetti ad essi collegati di cui apparentemente non si è modificata la definizione. Ad esempio [ figure 1]
se chiamo cerchio di centro C un insieme di punti equidistanti da C, a seconda che scelga la distanza euclidea o
quella urbanistica ottengo diversi concetti di cerchio.
• Anche le definizioni esplicite, come "x2 = x · x" con cui viene definito l'elevamento al quadrato, possono essere considerate degli assiomi: "x2" è l'oggetto che soddisfa la proprietà, cioè l'assioma, "x2 = x · x".
• Si è del resto visto che lo stesso concetto
può essere definito in modi diversi: la definizione scelta dipende da come
si decide di organizzare l'esposizione degli argomenti o, più in generale, dal gusto
personale. Non esiste "la" definizione; quando si consulta un trattato di
matematica, occorre tener presente, per capire le dimostrazioni o le argomentazioni svolte,
quali sono le definizioni adottate. Ad esempio
l'asse di un segmento posso definirlo
come l'asse di simmetria diverso dalla retta che lo contiene o come la retta che passa per il punto medio
del segmento e è ad esso perpendicolare: scelgo la prima definizione se ho già
introdotto il concetto di asse di simmetria, e se voglio dare una definizione che richiami
il significato di asse; con questa scelta il fatto che l'asse di simmetria
sia perpendicolare al segmento e passi per il suo punto medio diventa una proprietà
che posso dimostrare a partire dalla definizione. Potrei anche definirlo come
l'insieme dei punti equidistanti dai due estremi del segmento o, per far lo strano, come la retta
che dista da essi quanto la semilunghezza del segmento stesso.
• A volte, in matematica, si parla di concetti primitivi.
Con questo termine si intendono concetti il cui significato non viene esplicitato mediante
una definizione, ma è definito implicitamente dagli assiomi. Un esempio tipico,
visto sopra, è il concetto di probabilità. Nella voce
assiomi e loro modelli
vedrai presentazioni della geometria in cui vari concetti sono definiti
implicitamente dagli assiomi. Questo uso di "concetto primitivo" è diffuso
in matematica sin dalla fine del XIX secolo (lo hanno introdotto i matematici italiani
Peano, Pieri e Padoa), anche se in qualche libro di testo, buffamente, si usa tale
termine per indicare un concetto il cui significato è lasciato alla intuizione …
Linguaggio
I concetti matematici (e delle altre discipline) vengono spesso definiti prendendo a prestito
parole tratte dal linguaggio comune, che vengono però usate con un significato diverso.
Abbiamo visto vari esempi al proposito, come l'uso dell'aggettivo irrazionale [ le strutture numeriche]
o dei nomi direzione, angolo e lato [ figure 2]. Occorre poi tener presente che anche quando c'è sintonia tra uso matematico e uso comune di una parola, a volte quest'ultimo le impiega in modo più ristretto: in genere, descrivendo un tavolo come rettangolare si intende dire anche che non è quadrato [ rette tangenti e curve].
Vi sono anche altre situazioni di ambiguità. Si pensi alla definizione di triangolo isoscele
come "triangolo che ha due lati uguali". Qui stiamo intendendo che abbia "almeno due" lati uguali, ma potrebbe
averne anche tre. Se avessi voluto escludere questo caso avrei detto "che ha esattamente due lati uguali".
|
Oppure si pensi a quando si considerano due insiemi A e B con A contenuto in B ma diverso da B:
se ammettiamo che gli insiemi possano essere infiniti, possiamo avere che A e B sono in corrispondenza biunivoca
(ossia che esiste una funzione bigettiva da A a B, cioè iniettiva e avente come immagine B).
Si pensi al caso in cui A è l'insieme dei numeri pari e B è l'insieme dei numeri interi; A è
un sottoinsieme proprio di B (cioè è un sottoinsieme di B diverso da B stesso) ma ad ogni numero intero
(cioè ad ogni elemento di B) possiamo associare un numero pari (cioè un elemento di A): basta prendere il
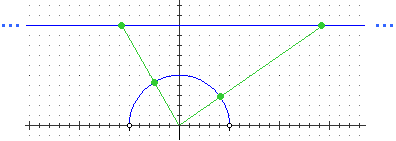
suo doppio. Oppure si pensi ad un segmento; possiamo incurvarlo fino a farlo diventare un semicerchio; a questo punto
possiamo mettere in corrispondenza ogni punto di una retta con un suo punto, come illustrato nella figura a fianco:
abbiamo messo il segmento in corrispondenza biunivoca con una retta, che lo può contenere infinite volte.
|  |
Cercando di comprendere una definizione, una proprietà o una dimostrazione,
possono, poi, manifestarsi dei fraintendimenti legati all'interpretazione dei connettivi o del significato complessivo di una
frase, che spesso è da affrontare in modo diverso rispetto al linguaggio comune.
Di questi aspetti abbiamo discusso, ad esempio, alle voci operatori logici
e tangenti e curve. Se ne discuterà anche più avanti.
Dimostrazioni
Una dimostrazione, in matematica, è il dedurre una proprietà a partire da altre assunte come vere o già dimostrate,
attraverso una sequenza di passaggi controllabili in modo oggettivo, ossia senza dar spazio a interpretazioni personali e usando procedimenti prestabiliti,
in modo che tutta la argomentazione sia verificabile in modo rigoroso.
• Vediamo uno dei molti esempi di dimostrazione già incontrati: la risoluzione di una equazione [ risoluz. equaz. 1]:
(1) |
x + 35 = 126 |
 equazione iniziale |
(2) |
x + 35 – 35 = 126 – 35 |
ho
applicato "–35" |
(3) |
x = 126 – 35 |
la funzione "+35" è stata annullata dalla funzione inversa "–35" |
(4) |
x = 91 |
ho effettuato i calcoli numerici |
In questo caso ho dimostrato che l'equazione (1) è equivalente all'equazione (4).
Prima ho concluso che (1) equivale a (2) usando la proprietà che se applico una funzione iniettiva a due input ottengo lo stesso output quando sono uguali gli input.
Ho poi usato il fatto che l'applicazione successiva di una funzione e della sua inversa fornisce un output uguale all'input per ottenere l'equivalenza tra (2) e (3).
Applicando il procedimento di calcolo per le sottrazioni ho infine ottenuto che (4) equivale a (3).
In breve, abbiamo concluso che:
(1) <==> (2), (2) <==> (3), (3) <==> (4)
(usando la notazione introdotta in risoluz.equaz.1).
E da ciò concludiamo, infine, che (1) <==> (4),
ossia x+35=126 <==> x=91.
In quest'ultimo passaggio abbiamo usato una proprietà del concetto di equivalenza che
nelle voci precedenti è sempre stata sottintesa: la transitività.
Infatti, in matematica, quando si introduce un concetto di eguaglianza o di equivalenza [cosa già fatta molte volte 
esempi]
si intende che si tratti di una relazione a 2 posti che sia:
riflessiva (ogni elemento deve equivalere a sé stesso),
simmetrica (se A equivale a B anche B deve equivalere ad A) e
transitiva (se A equivale a B e B equivale a C, A deve equivalere a C).
Si tratta di una cosa che sembra ovvia, ma,
nell'idea di esplicitare il più possibile i passaggi che si fanno nel corso di una dimostrazione,
è bene precisare anche queste proprietà, che non sono altro che gli assiomi che definiscono
il concetto di "(relazione di) equivalenza".
Scritti nella forma: x = x, x = y, se x = y e y = z allora x = z, vengono chiamati anche assiomi dell'eguaglianza.
La relazione "≤" tra numeri reali soddisfa le proprietà riflessiva (x≤x), transitiva (se x≤y e y≤z allora x≤z) ma non la simmetrica (x≤y non equivale a y≤x, se x≠y); anzi soddisfa la cosiddetta proprietà antisimmetrica:
se x ≤ y e x ≠ y allora NOT(y ≤ x).
Anche l'ordinamento alfabetico gode delle stesse proprietà. Lo stesso accade per la relazione di inclusione tra i insiemi
"⊂";
ad es. la antisimmetria corrisponde al fatto che
"se A⊂B e B⊂A allora A=B". Le relazioni che soddisfano le proprietà riflessiva, transitiva e antisimmetrica sono tutte dette relazioni d'ordine, ovvero tali proprietà sono gli assiomi di relazione d'ordine.
Richiamiamo anche una dimostrazione in ambito geometrico; quella [ triangoli] che:
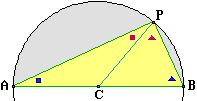
• i triangoli inscritti in un semicerchio sono rettangoli.
Abbiamo visto come facendo muovere il punto P della figura a lato si intuisca che ∠APB rimanga invariato, e quindi in particolare ampio 90° come nel caso in cui CP ⊥ AB. Si è visto anche che la proprietà può essere intuita pensando alla inscrizione di un rettangolo in un cerchio, e che queste intuizioni possono essere confermate con la dimostrazione seguente:
|
 |
| |
| (1) | ΔACP e ΔPCB sono isosceli in quanto A, P e B sono equidistanti dal centro C |
| (2) | ∠CAP = ∠APC e ∠PBC = ∠CPB per (1) e per il teorema "nei triangoli isosceli gli angoli opposti ai lati uguali sono uguali" |
| (3) | l'ampiezza di ∠APB (l'angolo in P di ΔABP) è uguale alla somma delle ampiezze di ∠APC e ∠CPB e quindi, per (2), alla somma delle ampiezze di ∠CAP e ∠PBC (gli angoli in A e B dello stesso triangolo) |
| (4) | ∠APB è ampio 90° per (3) e per il teorema "la somma della ampiezze degli angoli di un triangolo è 180°" |
|
La dimostrazione, ad essere rigorosi, dovrebbe essere più dettagliata. Nel passo (1) della dimostrazione abbiamo implicitamente usato le definizioni di triangolo isoscele (triangolo con almeno due lati uguali) e di cerchio di centro C (l'insieme dei punti equidistanti da C). Nel passo (3) abbiamo implicitamente usato la proprietà "se x=y e z=w allora x+z=y+w". Nel passo finale (4) abbiamo evitato di elencare i passaggi per risolvere rispetto ad α un sistema del tipo "α=β+γ & α+β+γ=180" (ottenendo α=90).
Nelle dimostrazioni si possono omettere dei passaggi, se è "evidente" (per chi elabora la dimostrazione e per le persone a cui si rivolge) come la argomentazione potrebbe essere completata (anche noi abbiamo sempre fatto così). Occorre trovare un equilibrio tra la spiegazione dei vari passaggi e la visione complessiva della dimostrazione (troppi dettagli fanno perdere il filo del ragionamento, troppo pochi rischiano di impedire il controllo delle argomentazioni).
In questa dimostrazione ho poi richiamato alcuni teoremi (ad es.: "la somma della ampiezze degli angoli di un triangolo è 180°"), ossia alcune proprietà che ho preso per buone, in quanto già dimostrate in precedenza.
E a loro volta questi teoremi [ triangoli] sono stati dimostrati nell'ipotesi di essere nel piano euclideo. In altre parole abbiamo sottinteso di essere nello spazio costituito dalle coppie di numeri reali e dotato della distanza euclidea.
E nelle varie dimostrazioni abbiamo usato concetti (distanza, retta, angolo, …) che avevamo definito in altre voci.
In definitiva, quando si dimostra una proprietà occorre precisare o che sia chiaro dal contesto quali sono le proprietà che si assumono per buone;
nel nostro caso abbiamo per es. assunto che un punto sia una coppia di numeri reali, che la distanza d(P1,P2) sia uguale a √( (x2 – x1)2 + (y2 – y1)2 ), …, ma anche che un numero reale sia …, che due numeri reali siano uguali se …, che una traslazione sia …, che una retta sia …
Le proprietà assunte per buone sono dette assiomi, in accordo con quanto già osservato sopra.
In genere non si hanno presenti tutte le assunzioni che via via si sono fatte e che intervengono implicitamente nel fare elaborazioni o dimostrando nuove proprietà,
ma bisogna avere ben in mente che le conclusioni a cui si arriva non sono verità assolute, ma solo conseguenze delle varie ipotesi.
Ricordiamo, ad es., che il teorema di Pitagora si può dimostrare solo se si definiscono piano, distanza, … in modi opportuni, e che nella realtà
vale in modo approssimato e solo in condizioni spaziali che siano in accordo con le ipotesi fatte
(non vale non solo nella navigazione in mare ma, come si vede in studi di fisica più avanzati, neanche per le grandi distanze spaziali).
Una proprietà per cui si sia trovata una dimostrazione, come abbiamo già detto, si chiama teorema, anche se, in genere, questa espressione si usa solo per le proprietà più importanti, che non sono banali da dimostrare e che si usano spesso nel corso della dimostrazione di altre proprietà.
Ad es. il fatto dimostrato nel punto precedente che
x+35=126 <==> x=91
a rigore è un teorema, ma si tratta di una proprietà che non ha senso memorizzare o annotare, in quanto siamo in grado di ricavarla nel caso in cui ci servisse.
Chiameremo invece "teorema" la proprietà dei triangoli inscritti in un semicerchio considerata in questo punto.
Osserviamo che a volte in matematica si parla di "dimostrazioni per assurdo." Come
esempio rimandiamo
alla dimostrazione che √p è irrazionale se p è un numero primo, in cui si ipotizza
che √p sia razionale e si prova che da ciò deriverebbe una contraddizione, ossia
una "assurdità".
A volte al posto della parola
"assioma" viene impiegata la parola "postulato". Sono
termini usati come sinonimi, anche se in filosofia spesso vengono
distinti: il primo a indicare una cosa di per sé valida, una verità evidente,
il secondo a indicare una affermazione non dimostrata né dimostrabile, ma
necessaria e accettata, anche se di per sé non evidente. In matematica questa distinzione
non ha alcun senso, come si evince da molte considerazioni svolte in questa voce, ad esempio discutendo
di che cosa è un
modello matematico, e in altre voci precedenti (e
seguenti). Questa distinzione
veniva usata anche in ambito matematico più di una secolo fa, quando la matematica non era
ancora una
disciplina autonoma.
Ad esempio la sistemazione della geometria che nel 300 a.C. aveva dato Euclide
()
ha poco a che fare con ciò che ora si intende per sistema di assiomi: gran parte delle dimostrazioni
si basavano su argomentazioni intuitive e gli assiomi erano intesi nel senso "filosofico" sopra accennato:
erano considerati dei punti di partenza obbligatori che rappresentavano delle verità evidenti, non delle
regole del gioco che possono essere assunte o no a seconda delle esigenze. Sono, invece, assai vicini alla concezione matematica di
"assioma" le regole che si mettono alla base di un gioco, come ad esempio nel caso della dama
(). Su ciò si tornerà nella voce
Assiomi e loro modelli.
Osserviamo, ancora, che vi sono proprietà che risultano evidenti ma che non si
è ancora riusciti a dimostrare, e non si sa se si riuscirà mai a farlo. Un esempio
di problema aperto di questo genere puoi trovarlo nel quesito 8
qui.
Simboli logici
Un altro esempio:
• la dimostrazione che ogni numero maggiore di 1 ha reciproco minore di 1.
Possiamo scrivere più in breve la proprietà così:
∀x ( x > 1 ==> 1/x < 1) dove
∀x P possiamo leggerlo come "per ogni x la condizione P è vera" e
P ==> Q possiamo leggerlo come "se P è vera allora è vera Q",
per cui possiamo leggere la espressione precedente come "per ogni x, se x>1 allora 1/x<1".
Si può usare anche la notazione abbreviata:
∀x > 1 (1/x < 1) leggibile come "1/x < 1 per ogni x maggiore di 1".
Queste scritture, che usano simboli invece di parole, hanno il vantaggio di essere leggibili più facilmente e in modo meno ambiguo.
Una dimostrazione possibile è la seguente:
(1) Suppongo che x > 1.
(2) La funzione reciproco (x 
1/x) è decrescente sia in (-∞,0) che in (0,∞).
(3) Quindi essa è in particolare decrescente nell'intervallo (0,∞) che contiene i numeri maggiori di 1.
(4) Dunque applicata ai due membri di (1) ne inverte l'ordine: 1/x < 1/1, ossia 1/x < 1.
[la x usata in x 1/x serve solo per
descrivere la funzione;
avrei potuto usare equivalentemente z 1/z; non è la stessa x della proprietà che
si vuole dimostrare]
La dimostrazione è finita: abbiamo fatto vedere che se x>1 è vera allora è vera 1/x<1.
Nel passo (2) della dimostrazione abbiamo usato una
proprietà della funzione reciproco
che abbiamo preso per buona, supponendo di averla già dimostrata.
Nel passo (4) abbiamo usato la
definizione di funzione decrescente.
Nel passo (3) abbiamo usato questa forma di ragionamento:
se è vera "P e Q" allora (in particolare) è vera Q, ovvero:
P & Q ==> Q.
• Vale anche la proprietà seguente?
∀x ( x > 1 <==> 1/x < 1)
leggibile come "per ogni x, x>1 equivale a 1/x<1" o anche "per ogni x, x>1 se e solo se 1/x<1".
La "doppia freccia" ricorda il fatto che questa proprietà potrei scriverla:
∀x ( (x > 1 ==> 1/x < 1) & (1/x < 1 ==> x > 1) )
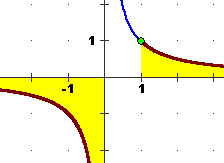
Si capisce subito, pensando al grafico di x 1/x (vedi figura a fianco), che questa proprietà è falsa.
Dal grafico capiamo subito che è invece vera:
∀x ( 1/x < 1 <==> (x < 0 V x > 1) )
[V sta per OR]
|  |
|
Riassumendo, è vera: |
∀x ( x > 1 ==> 1/x < 1) |
|
mentre non lo è: |
∀x ( 1/x < 1 ==> x > 1) |
|
Anche senza pensare al grafico, per concludere che quest'ultima proprietà è falsa
bastava osservare che ci sono degli x, in particolare gli x negativi, per cui
x>1 è falso nonostante che 1/x<1 sia vero.
|
In altre parole il fatto che ∀x ( 1/x < 1 ==> x > 1) sia falsa
equivale alla verità di:
∃x ( 1/x < 1 & NOT (x > 1) )
dove "∃x …" si legge "esiste x tale che …".
Che origine hanno i simboli ∃ e ∀ ?
Il primo simbolo fu introdotto (nel 1900) da Peano; è una "E" rovesciata che richiama l'iniziale di "esiste".
Il secondo simbolo fu introdotto dal tedesco Gentzen (nel 1935); è una "A" rovesciata, per richiama l'inziale di "all"
che (in tedesco come in inglese) vuol dire "tutti". I due quantificatori vengono in genere chiamati, rispettivamente,
esistenziale e universale.
L'uso di simboli come quelli appena introdotti spesso (non sempre!)
consente di esprimere proprietà e condizioni in modo più efficace rispetto al linguaggio verbale.
Consideriamo ad es. il concetto di limite.
Di fronte a limx → ∞ f(x) = L (per x che tende all'infinito f(x) tende al numero L) la formulazione verbale
«comunque fissi un numero positivo ε posso trovare x oltre il quale gli input x producano output f(x) che distino da L meno di ε»
non è di facile comprensione se non si ha già in testa il concetto e la sua interpretazione grafica.
Per una persona allenata ad usare i simboli, è più intellegibile (e facile da produrre) la descrizione seguente:
∀ε>0 ∃x ∀x>x d(f(x), L) < ε
ovvero:
∀ε>0 ∃x ∀x>x |f(x)-L| < ε
Analogamente lim x → h+ f(x) = ∞
(«comunque fissi K posso trovare δ tale che gli input maggiori e distanti da h meno di δ producano output superiori a K»)
e lim x → h f(x) = –∞ («comunque fissi K posso trovare δ tale che gli input diversi e distanti meno di δ da h producano output inferiori a K»)
diventano per esempio:
∀K ∃δ ∀x
(h,h+δ) f(x) > K
e
∀K ∃δ ∀x(h-δ,h) U (h,h+δ) f(x) < K
Non si tratta di formule da imparare a memoria. L'importante è aver compreso il concetto e, eventualmente,
saperlo esprimere costruendo una formula che lo descriva.
Per fare dimostrazioni rigorose occorrerebbe specificare meglio i passaggi precisando anche le regole
che si usano per trasformare le formule in cui compaiono gli operatori logici
(OR - disgiunzione, AND - congiunzione, NOT - negazione) e altri simboli logici come i simboli
∀ e ∃ (detti quantificatori
perché indicano la quantità degli oggetti - tutti o qualcuno - che soddisfano una certa proprietà),
e i simboli
<==> e ==> .
C'è un settore della matematica, la logica matematica
(nato nella prima metà del XX secolo), che si occupa
dello studio di queste regole, anche attraverso la precisazione, mediante opportuni assiomi, del significato dei simboli logici.
Noi, qui, eviteremo di formalizzare fino a tal punto le dimostrazioni.
Useremo, tuttavia, spesso i simboli logici per rendere più
sintetica e meno ambigua la descrizione delle proprietà da provare o dei
passaggi dimostrativi compiuti.
In alcuni esercizi potrai trovare la descrizione di qualche trasformazione di formule contenenti simboli logici.
Nota 1. Usare l'espressione "∀x" al posto di "ogni x" è sbagliato. Si può usare "∀x" solo assieme a una condizione per precisare che la si intende riferire a tutti gli x. Se, ad esempio, si vuole indicare che una equazione è vera qualunque numero si sostituisca alla incognita x, si può scrivere che le sue soluzioni formano l'insieme R, non che le sue soluzioni sono ∀x. A rigore non è neanche corretto dire che ogni x è soluzione, in quanto x è solo il nome usato in questo caso per l'incognita; si dovrebbe più semplicemente dire che ogni numero è soluzione.
Nota 2. Il simbolo ==> (spesso chiamato di
implicazione) sintetizza l'uso di "se … allora …" che si fa in matematica, e che è un po' diverso da quello che si fa nel linguaggio comune. Ad es. nel controllare la validità di una condizione come per ogni x e y appartenenti ad I, se x > y allora f(x) > f(y) ci si limita a controllare se è vero che f(x) > f(y) nei casi in cui
x > y, dato che la falsità di f(x) > f(y) nel caso in cui x ≤ y non ci crea problemi. In altre parole, una condizione del tipo A ==> B viene considerata falsa solo nel caso in cui A sia vera e B sia falsa.
Secondo questa interpretazione di "se … allora …" una frase come "se mia nonna avesse avuto le ruote sarebbe stata una carriola" è vera in quanto mia nonna non aveva le ruote, mentre nel linguaggio comune è considerata solo un nonsenso. Anche "se il ghiaccio bolle allora evapora" non è certo considerato un principio fisico vero, mentre secondo l'interpretazione che usualmente si fa in matematica di "se … allora …" sarebbe una proposizione vera, in quanto non può verificarsi che il ghiaccio bolla.
Infine occorre tener presente che vi sono casi in cui con dei "se … allora …" si costruiscono delle frasi di cui non ha senso discutere se sono vere o false. Si pensi, ad es., alla frase "se piove prendi l'ombrello" o, in matematica, a "se x ≥ 0 allora prendi x come valore assoluto di x". Queste frasi indicano l'associazione a una certa risposta di una determinata azione, sono analoghe a dei comandi del tipo IF … THEN … di un linguaggio di programmazione o di un foglio di calcolo elettronico.
In tutti questi casi non ha senso impiegare il simbolo ==> .
x > 1 <==> 1/x < 1 viene spesso letta come "x > 1 se e solo se 1/x < 1";
da qui segue l'uso di leggere x > 1 ==> 1/x < 1 anche come "x > 1 solo se 1/x < 1".
Quest'ultimo è un uso del tutto convenzionale fatto dai matematici,
spesso comodo per distinguere con un "se" e un "solo se" i due versi della
doppia freccia <==> :
nel linguaggio comune "solo se" quasi sempre coincide con "se e solo se".
E anche in matematica, quando non si sta enunciando una definizione o un teorema, a volte si usa "solo se" in questo modo.
Osserviamo che spesso in matematica si usa l'espressione "sse" come abbreviazione di
"se e solo se".
Considerazioni analoghe su altri simboli logici sono state svolte alla voce operatori logici. Considerazioni più generali sono presenti alla voce rette tangenti e curve.
Altri sviluppi
In una successiva voce, assiomi e loro modelli, approfondiremo alcune delle considerazioni svolte qui,
e metteremo a fuoco un altro uso, quasi simmetrico, della parola modello a
cui spesso si ricorre in matematica (e in altre scienze).
Esercizi:
e fogli di esercizi successivi
altri collegamenti [nuova pagina]
