Linguaggio
I concetti matematici (e delle altre discipline) vengono spesso definiti prendendo a prestito parole tratte dal linguaggio comune, che vengono però usate con un significato diverso. Cose analoghe (in cui termini o frasi intere vengono usate in modo differente) accadono anche nelle argomentazioni matematiche. Richiamiamo alcuni esempi.
• Mentre in matematica con angolo si intende una parte illimitata di piano, nel linguaggio comune con questa parola si indica una zona dell'angolo vicina al vertice: quando si dice «la sedia che sta in quell'angolo» ci si riferisce a quella che è vicina al vertice di esso (ogni altra sedia che sta nella stanza - se questa non ha una forma "strana" - sta in quell'angolo). Si noti che la parola stessa lato in matematica è usata con un significato quando è riferita a un poligono (indica un segmento) e con un altro quando è riferita a un angolo (indica una semiretta).
• Nell'usuale comunicazione - anche quando si parla di matematica - dicendo «ho un tavolo rettangolare», «non arrivo a 38° di febbre», «disegna un'ellisse» … voglio dire anche che il tavolo non è quadrato, informare che la mia temperatura corporea supera i 37°, chiedere di non disegnare un cerchio, … in quanto altrimenti avrei specificato diversamente la forma del tavolo, la mia temperatura, la figura da disegnare, …
Nell'enunciare una proprietà o una definizione matematica, invece, se parlo di un rettangolo o di una ellisse o ad esempio di un trapezio non escludo che sia, rispettivamente, un quadrato o un cerchio o un rettangolo, se scrivo
• Nella definizione di triangolo isoscele come "triangolo che ha due lati uguali" si intende che esso abbia "almeno due" lati uguali, ma potrebbe averne anche tre. Se avessi voluto escludere questo caso avrei detto "che ha esattamente due lati uguali".
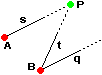
| • Nel linguaggio comune si dice che (vedi la figura a destra) muovendosi da A e B verso il punto P si va nella stessa direzione: si è diretti verso la stessa meta. In matematica invece le due traiettorie (ossia le semirette s e t) vengono considerate di direzione diversa, mentre si considerano ugualmente dirette solo traiettorie come s e q. |  |
• Nel linguaggio comune mentre della linea A sotto tracciata si dice che è una curva oppure un profilo, una traiettoria, … curvilinea, la stessa cosa non viene detta di B, che ha andamento rettilineo, né di C o di D, che presentano dei punti angolosi, ossia dei punti in cui, percorrendo la linea da un capo all'altro, si arriva con una direzione e se ne riparte con un'altra.
![]()
In matematica, invece, tutte e quattro le linee vengono chiamate curve; si dice eventualmente che A è una curva non rettilinea.
• I numeri reali non periodici, non essendo razionali, vengono detti anche irrazionali, ma ciò non significa che le loro cifre si susseguano in modo caotico, come si potrebbe pensare riferendosi all'uso dell'aggettivo "irrazionale" come "privo di ogni logica": ad esempio nel numero irrazionale 7.12112111211112111112 (in cui via via si allunga la sequenza di 1) le cifre si susseguono secondo un ben preciso procedimento.
| • Nelle esperienze comuni si ha a che fare con insiemi finiti di oggetti e non viene da pensare che un insieme possa contenere strettamente un altro e nello stesso tempo essere in corrispondenza biunivoca con esso. Ma in matematica l'insieme dei numeri interi contiene quello dei numeri pari e nello stesso tempo ad ogni numero intero posso associare il suo doppio, ossia un numero pari. Oppure si pensi ad un segmento; posso incurvarlo fino a farlo diventare un semicerchio; posso quindi mettere in corrispondenza ogni punto di una retta con un punto di esso, come illustrato nella figura a fianco; un segmento può essere messo in in corrispondenza biunivoca con una retta, che lo può contenere infinite volte! |  |
•
Vi è poi, più in generale, il fatto che la semantica dei linguaggi formali che si usano in matematica (ed informatica) non ha molto a che fare con quella del linguaggio naturale.
In quest'ultimo vi è una fortissima dipendenza dal contesto,
che può modificare profondamente il significato di una
frase. Due esempi:
– una frase come «ha un vestito giallo» può assumere una gamma di
significati che va da «ha un vestito completamente giallo» a «ho un vestito in cui c'è anche del giallo»;
se il vestito è a fiori gialli dietro i quali si intravede uno sfondo bianco l'affermazione «ha un vestito giallo»
deve essere interpretata come "vera" o "falsa"?
– l'affermazione «Giorgio questa volta ha preso la sufficienza» non fornisce, comunemente, solo un'informazione su come gli è
andato il compito in classe di Inglese, ma dice anche che Giorgio di solito non va un gran che bene in Inglese;
tuttavia se sapessimo che Giorgio è il primo della classe in Inglese interpreteremmo la frase diversamente,
e del voto non penseremmo solo che è maggiore o uguale a 6 (supponendo che 6 sia il minimo voto sufficiente) ma che è 6 o non lo supera di molto.
Questa dipendenza dal contesto è presente anche in matematica, quando ci si esprime usando il linguaggio comune.
Quanto detto vale, in particolare quando si usano i connettivi linguistici "e", "o" e "non".
Ad esempio le frasi «Mario entrò nella casa e si tolse le scarpe» e «Mario si tolse le scarpe e entrò nella casa»
rappresentano indubbiamente situazioni diverse. Nella frase «Pierino accendeva e spegneva il televisore in
continuazione» il connettivo "e" collega due forme verbali ("accendeva" e "spegneva") che descrivono addirittura azioni mutuamente incompatibili.
Nel linguaggio naturale, poi, un connettivo in qualche caso collega in realtà due affermazioni:
«l'automobile di Gianni è bella e veloce» è equivalente a «l'automobile di Gianni è bella e
l'automobile di Gianni è veloce»; in «l'automobile di Gianni è bianca e rossa» la "e" serve invece a costruire un nuovo aggettivo a partire da "bianco" e "rosso".
Qualche esempio con "o". In «dall'accento direi che è
genovese o ligure» capiamo che "o" è da intendersi come "inclusivo", mentre in «lo vuoi o no?» capiamo che dobbiamo considerarlo "esclusivo". Ma in
«vogliamo rose rosse o bianche» se non conosciamo il contesto in cui viene formulata la richiesta
non possiamo capire se va bene che vi siano rose sia rosse che bianche o se devono essere tutte rosse o tutte bianche.
Per il "non" si possono fare esempi analoghi. «Non è falso ciò che ha detto» non sempre vuol dire che ha detto il "vero":
potrebbe aver fatto un'affermazione che contiene degli elementi di verità.
• Anche l'uso di "se … allora …" che si fa in matematica è un po' diverso da quello che si fa nel linguaggio comune. Ad esempio nel controllare la validità di una condizione come per ogni x e y appartenenti ad I, se
Infine occorre tener presente che vi sono casi in cui con dei "se … allora …" si costruiscono delle frasi di cui non ha senso discutere se sono vere o false.
Si pensi, ad esempio, alla frase "se piove prendi l'ombrello" o, in matematica, a "se
Spesso, in matematica, per esprimere il fatto che la condizione A e la condizione B sono equivalenti si usa dire "A se e solo se B", e
al posto di "se x > 1 allora 1/x < 1" si usa