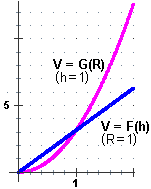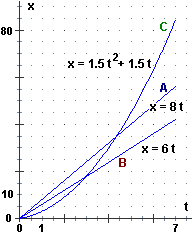Derivata e differenziale di una funzione
Alle voci  pendenza 2,
pendenza 2,  rette tangenti e curve e
rette tangenti e curve e  velocità di variazione vengono proposte diverse situazioni e idee che motivano e introducono il concetto di derivata, uno dei più importanti della matematica. Esamina almeno una di tali voci prima di intraprendere la lettura di questa.
In alternativa, per una presentazione più sintetica, guarda direttamente la scheda La derivazione di funzioni
velocità di variazione vengono proposte diverse situazioni e idee che motivano e introducono il concetto di derivata, uno dei più importanti della matematica. Esamina almeno una di tali voci prima di intraprendere la lettura di questa.
In alternativa, per una presentazione più sintetica, guarda direttamente la scheda La derivazione di funzioni
 qui
qui
 Introduzione al concetto di differenziale
Introduzione al concetto di differenziale
La messa a punto del concetto di derivata di una funzione (a 1 input e 1 output, e  continua) ha l'obiettivo di descrivere in modo opportuno come l'output di essa tende a variare al variare dell'input. Per capire meglio questo obiettivo partiamo da un esempio apparentemente lontano.
continua) ha l'obiettivo di descrivere in modo opportuno come l'output di essa tende a variare al variare dell'input. Per capire meglio questo obiettivo partiamo da un esempio apparentemente lontano.
• Avrai sentito parlare di "tasso tendenziale di inflazione", "aumento tendenziale della produzione", …. Si tratta di indicatori economici con cui si cerca di descrivere la situazione attuale e individuare come essa evolverebbe se le cose continuassero ad andare come negli ultimi tempi:
quando si dice che l'aumento annuo tendenziale della esportazione di un certo bene ad ottobre è stato di 45 milioni 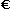 si intende che tale è il valore di cui essa è cresciuta rispetto all'ottobre dell'anno prima; in tal caso per il prossimo quadrimestre (1/3 di anno) prevediamo un incremento tendenziale di 15 milioni
si intende che tale è il valore di cui essa è cresciuta rispetto all'ottobre dell'anno prima; in tal caso per il prossimo quadrimestre (1/3 di anno) prevediamo un incremento tendenziale di 15 milioni  (1/3·45 = 15): questo sarebbe l'aumento se la produzione continuasse a crescere proporzionalmente al tempo trascorso con un incremento di 45 milioni
(1/3·45 = 15): questo sarebbe l'aumento se la produzione continuasse a crescere proporzionalmente al tempo trascorso con un incremento di 45 milioni 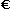 /anno.
/anno.
Naturalmente non è detto che sarà questo l'effettivo aumento: si tratta solo di una approssimazione, che sarà tanto più buona quanto più la variazione della produzione si manterrà proporzionale al tempo trascorso (con fattore di proporzionalià pari all'aumento medio dell'ultimo anno).
• Analogamente, se nell'ultimo anno la temperatura media sulla Terra fosse salita di 0.04° potremmo dire che questa è la tendenza con cui varia la temperatura sul nostro Pianeta. Potremmo prevedere che tra 5 anni la temperatura sarà variata di 0.04·5 = 0.2 gradi. Potremmo fare anche previsioni per tempi più lontani; ma sarebbero molto meno attendibili: l'andamento potrebbe cambiare; si potrebbe anche entrare in una fase in cui la temperatura si abbassa.
La derivazione di una funzione F (continua) è qualcosa che potremmo intuitivamente descrivere come lo studio della variazione tendenziale di F(x) (non rispetto al tempo, ma a una generica variabile x). Useremo il termine differenziale di F(x), e la notazione d F(x), per indicare la variazione tendenziale di F(x), ossia la variazione che F(x) subirebbe passando da x a x+Δx se in quell'intervallo le variazioni dell'output fossero proporzionali a quelle dell'input, cioè se la funzione proseguisse con grafico rettilineo, cioè fosse  lineare. lineare.
Nel caso illustrato a fianco è tracciato il grafico di una funzione F e la retta secondo cui il grafico proseguirebbe se proseguisse con lo stesso andamento che aveva nel punto x. Passando da x a x+Δx la funzione cambia andamento; a un certo punto inizia addirittura a decrescere. In questo caso la mia approssimazione di ΔF(x), ossia della variazione effettiva di F(x), con d F(x) è buona se Δx è piccolo, man mano peggiora al crescere di Δx.
È un po' come nel caso della produzione: posso supporre che per qualche mese o anno le esportazioni continuino a crescere più o meno allo stesso modo. Ma man mano che mi allontano nel tempo le mie previsioni sono sempre più azzardate.
Vediamo tre tipici esempi d'uso del concetto di differenziale.
| 
Il differenziale di F (nel punto x
e rispetto alla variazione Δx).
Per Δx→0 dF(x) ≈ ΔF(x) |
 (A) Nel caso di F: x
(A) Nel caso di F: x  √x si può trovare (vedremo come
√x si può trovare (vedremo come  più avanti) che vicino a x=1 il grafico di F è approssimabile con una retta di pendenza 1/2, ossia che la variazione di F(x) è circa 1/2 di quella di x. Potremmo dire che qui le variazioni di F(x) sono tendenzialmente uguali a 0.5Δx (con notazione compatta: Δ√x ≈ 0.5Δx): 0.5Δx è il differenziale che esprime la variazione tendenziale di √x per x = 1.
più avanti) che vicino a x=1 il grafico di F è approssimabile con una retta di pendenza 1/2, ossia che la variazione di F(x) è circa 1/2 di quella di x. Potremmo dire che qui le variazioni di F(x) sono tendenzialmente uguali a 0.5Δx (con notazione compatta: Δ√x ≈ 0.5Δx): 0.5Δx è il differenziale che esprime la variazione tendenziale di √x per x = 1.
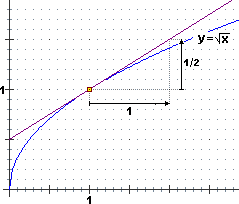 |
Per input vicini a 1 la funzione radice quadrata ha grafico approssimabile con una retta di pendenza 0.5.
Quindi se mi allontano da 1 di Δx la variazione Δ√x della funzione è circa 0.5Δx. |
Quindi se (senza calcolatrice) voglio approssimare rapidamente quanto vale √1.1, poiché √1=1 e 1.1 dista Δx = 0.1 da 1, posso assumere come valore √1+0.5Δx = 1+0.5·0.1 = 1.05. Se usassi la calcolatrice troverei 1.0488. La approssimazione 1.05 è soddisfacente.
Analogamente √0.9 è circa √1 più il differenziale 0.5Δx con Δx = –0.1, ossia 1+0.5·(–0.1) = 0.95 (con la calcolatrice avrei 0.9487).
Più in generale, per x vicino a 1, √x è approssimabile con 1+0.5(x–1) (y=1+0.5(x–1) è la retta con pendenza 0.5 passante per (1,1)): √1.08 ≈ 1+0.5(1.08–1) = 1+0.5·0.08 = 1.04.
Nota. C'è, invero, qualche differenza tra il caso della variazione tendenziale della produzione e quello del differenziale di una funzione: là valutavamo il fattore di proporzionalità che lega variazione del tempo e variazione della produzione tenendo conto dell'andamento del fenomeno nell'ultimo anno, qui determiniamo il fattore di proporzionalità che lega variazione dell'input e variazione dell'output tenendo conto solo dell'andamento della funzione in un punto, non in un intervallo di lunghezza fissata.
 (B) Supponiamo, invece, di dover calcolare con un programma, per qualche attività di tipo teconologico, la radice quadrata di molti valori approssimati e di voler valutare con quale precisione prendere i risultati. Più precisamente supponiamo che i nostri dati abbiano una precisione relativa del 10%, nel senso che [
(B) Supponiamo, invece, di dover calcolare con un programma, per qualche attività di tipo teconologico, la radice quadrata di molti valori approssimati e di voler valutare con quale precisione prendere i risultati. Più precisamente supponiamo che i nostri dati abbiano una precisione relativa del 10%, nel senso che [ calc. approssimato] l'errore possa essere al più il 10% del valore. Vogliamo stimare la precisione relativa delle radici quadrate dei dati.
calc. approssimato] l'errore possa essere al più il 10% del valore. Vogliamo stimare la precisione relativa delle radici quadrate dei dati.
Il valore esatto di un dato può differire dal valore misurato Q di ΔQ = 10%·Q, ossia può arrivare ad essere Q+10%Q. Ad es. il dato 70 corrisponde a un valore vero che può variare del 10% da 70, ossia compreso tra 70-7 e 70+7.
– √(Q+10%Q) = √(Q·(1+10%)) = √Q·√(1+10%).
– Ho appena visto che √(1+Δx) ≈ √1+0.5·Δx = 1+Δx. Quindi √(1+10%) ≈ 1+5%.
– Perciò √(Q+10%Q) ≈ √Q·(1+5%) = √Q + 5%√Q.
Concludendo se Q ha una precisone relativa del 10%, √Q ha una precisone relativa del 5%, migliore di quella del dato su cui si è operato.
Ad es. se come calcolo di una radice quadrata di un certo dato (dei miei dati con precisione del 10%) ottengo 8.367, essendo 5%·8.367 = 0.41, posso approssimare il valore con 8.37±0.42, o con 8.4±0.5.
 (C) Un altro esempio d'uso. Voglio determinare
lim x → 1(√x – 1) / (x – 1).
(C) Un altro esempio d'uso. Voglio determinare
lim x → 1(√x – 1) / (x – 1).
Il passaggio al limite conserva i rapporti [ limiti]; mi riconduco a limx → 1(√x-1) / limx → 1(x-1), ma ottengo 0/0, che è indefinito.
limiti]; mi riconduco a limx → 1(√x-1) / limx → 1(x-1), ma ottengo 0/0, che è indefinito.
Posso però ricorrere a quanto appena visto: √x quanto più x è vicino a 1 tanto meglio è approssimabile con 1+0.5(x–1), la funzione lineare con grafico di pendenza 0.5 passante per (1,1). Quindi per x →1 la funzione di cui voglio trovare il limite tende a comportarsi come quella ottenuta sostituendo questo termine a √x:
limx→1(√x–1) / (x–1) = limx→1(1+0.5(x–1) – 1) / (x–1) = limx→10.5(x–1)/(x–1) = limx→10.5 = 0.5
[Ho sostituito (x–1)/(x–1) con 1 in quanto per x 1 i due termini sono equivalenti, e quindi hanno lo stesso comportamento per x→1. Potevo operare anche trasformando, con un procedimento inverso alla razionalizzazione [
1 i due termini sono equivalenti, e quindi hanno lo stesso comportamento per x→1. Potevo operare anche trasformando, con un procedimento inverso alla razionalizzazione [ strutture numeriche], la funzione in 1/(√x+1) - prova a farlo - che per x→1 tende a 0.5]
strutture numeriche], la funzione in 1/(√x+1) - prova a farlo - che per x→1 tende a 0.5]
Esercizio: testo e soluzione
 Definizione di coefficiente differenziale e di funzione derivata
Definizione di coefficiente differenziale e di funzione derivata
È facile capire che la funzione lineare che abbiamo usato per  approssimare l'andamento di una funzione continua F ed esprimerne il differenziale nell'input x ha per grafico la tangente al grafico di F nel suo punto di ascissa x. Interpretando nel caso specifico dei grafici di funzioni quanto in un'altra voce [
approssimare l'andamento di una funzione continua F ed esprimerne il differenziale nell'input x ha per grafico la tangente al grafico di F nel suo punto di ascissa x. Interpretando nel caso specifico dei grafici di funzioni quanto in un'altra voce [ rette tangenti e curve] è discusso più in generale per le tangenti alle curve, possiamo dunque precisare nel modo seguente come si determini il coefficiente direttivo di questa funzione lineare.
rette tangenti e curve] è discusso più in generale per le tangenti alle curve, possiamo dunque precisare nel modo seguente come si determini il coefficiente direttivo di questa funzione lineare.
Se indichiamo con x0 il particolare input considerato, questo coefficiente si chiama coefficiente differenziale o derivata di F in x0 e si definisce come la pendenza della retta a cui tende la retta PQ sotto raffigurata (P è il punto del grafico di F di ascissa x0 e Q è quello di ascissa x0+h) al tendere di h a 0 (con h abbiamo indicato, per brevità, la variazione Δx dell'input):
| lim h → 0 | F(x0 + h) – F(x0) |
| ——————— |
| h |
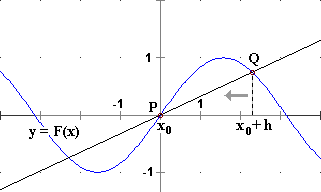
Δx = h ΔF(x) = yQ – yP = F(x0 + h) – F(x0)
P = (x0, F(x0)) Q = (x0+h, F(x0+h)) | 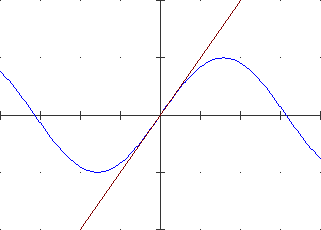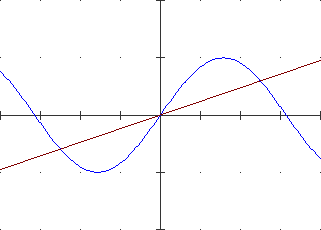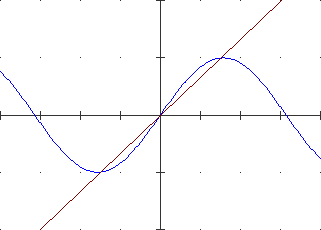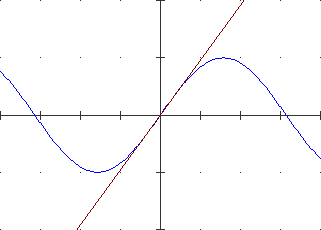 |
|  |
Nota. Nelle immagini abbiamo considerato variazioni h positive, ma è da intendersi che può essere anche h < 0. D'altronde, nel caso raffigurato, l'immagine animata a destra può essere pensata anche con h = –3, –2.5, –2, … immaginando che il punto Q sia il punto che la retta ha in comune con la parte del grafico a sinistra di P. Il numero (F(x0+h)-F(x0)/h, che esprime la  pendenza media del grafico di F tra x0 e x0+h, viene chiamato anche rapporto incrementale di punto iniziale x0 e passo h (è il rapporto tra la variazione dell'output e l'incremento dell'input, o il suo decremento, se h è negativo).
pendenza media del grafico di F tra x0 e x0+h, viene chiamato anche rapporto incrementale di punto iniziale x0 e passo h (è il rapporto tra la variazione dell'output e l'incremento dell'input, o il suo decremento, se h è negativo).
Esempio D. Determiniamo il coefficiente differenziale (o derivata) di x  x2 in 1.
x2 in 1.
| lim h→0 | (1 + h)2 – 12 |
| ————— |
| h |
| =
|
| lim h→0 | 1 + 2h + h2 – 1 |
| —————— |
| h |
| =
|
| =
|
| =
|
|
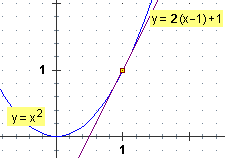 |
Dunque per x→1 la funzione è approssimabile con una funzione lineare di coefficiente direttivo 2.
Una semplice applicazione: stimiamo velocemente 1.012.
– per x→1 Δx2 è approssimabile con 2Δx
– 1.01 = 1+0.01; Δx = 0.01
– passando da x=1 a x=1.01 x2 aumenta di circa 2Δx = 0.02
– 1.012 è circa 1 + 0.02 = 1.02
Facendo i calcoli per esteso (o con una calcolatrice) avremmo ottenuto 1.0201.
|
Se ci ricordiamo [ funzione 1] che il grafico di x funzione 1] che il grafico di x  √x si ottiene dalla parte destra del grafico di x √x si ottiene dalla parte destra del grafico di x  x2 scambiandone le x con le y, ritroviamo quanto preannunciato x2 scambiandone le x con le y, ritroviamo quanto preannunciato  nell'esempio iniziale A: la derivata (coefficiente differenziale) di √x in 1 è 1/2. nell'esempio iniziale A: la derivata (coefficiente differenziale) di √x in 1 è 1/2. |
 Con derivare una funzione (a 1 input e 1 output, e continua) F si intende ottenere da essa una nuova funzione F' – la funzione derivata o, più in breve, la derivata – che descriva al variare di x la pendenza del grafico di F nel punto di ascissa x. Come abbiamo appena visto, questa non è altro che la funzione che a x associa il coefficiente differenziale di F in x.
Con derivare una funzione (a 1 input e 1 output, e continua) F si intende ottenere da essa una nuova funzione F' – la funzione derivata o, più in breve, la derivata – che descriva al variare di x la pendenza del grafico di F nel punto di ascissa x. Come abbiamo appena visto, questa non è altro che la funzione che a x associa il coefficiente differenziale di F in x.
È da ciò che si è originato l'uso del termine "derivata" anche per indicare il coefficiente differenziale,
anche se inizialmente il nome era usato solo per indicare la funzione-derivata. Il coefficiente differenziale in p viene quindi indicato con F'(p), e il differenziale con F'(p)Δx (se x è la variabile di input). Vedremo, più avanti, altre notazioni.
La funzione originaria si chiama primitiva (o antiderivata) della nuova funzione così ottenuta.
Vi sono alcuni casi semplici in cui è immediato determinare la funzione derivata. Se una funzione F è costante (ad es. la temperatura in un buon frigorifero in funzione del tempo, a patto che esso non venga mai aperto), del tipo F(x) = k, al variare dell'input (x = tempo) si ha sempre lo stesso output (la stessa temperatura); quindi ΔF(x) vale sempre 0. Sia da questo fatto che dal fatto che si tratta di un grafico orizzontale e quindi con pendenza nulla, possiamo subito dedurre che F'(x) = 0 per ogni x.
Se la funzione, invece, ha uscite che crescono proporzionalmente al crescere dell'input (ad es. il peso di un contenitore cilindrico al variare dell'acqua in esso contenuta), ossia se è una funzione polinomiale di 1° grado, del tipo F(x) = ax + b, la funzione derivata dovrà avere un valore costante e positivo (ad ogni tot di acqua in più corrisponde un altro tot di peso in più, indipendentemente da quanta acqua ci fosse prima). La cosa può essere dedotta più precisamente pensando al grafico: è una retta inclinata; la sua pendenza è la derivata: F'(x) = a per ogni x. In altre parole la funzione lineare che approssima F è F stessa, che ha come coefficiente direttivo a.
Alla voce  pendenza 2 è stato introdotto in modo intuitivo, con vari esempi, il concetto di funzione-derivata. Esso in qualche modo generalizza il passaggio dal profilo altimetrico di una strada al grafico di come varia la sua pendenza:
pendenza 2 è stato introdotto in modo intuitivo, con vari esempi, il concetto di funzione-derivata. Esso in qualche modo generalizza il passaggio dal profilo altimetrico di una strada al grafico di come varia la sua pendenza:
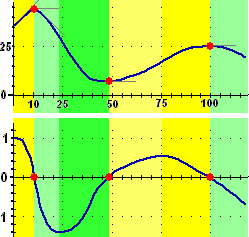 | – Quando il percorso sale la pendenza è positiva.
– Nei punti in cui il percorso è orizzontale la pendenza è 0.
– Quando il percorso scende la pendenza è negativa.
– Quando la salita si addolcisce o la discesa si accentua la pendenza scende.
– Quando la discesa si addolcisce o la salita si accentua la pendenza sale. |
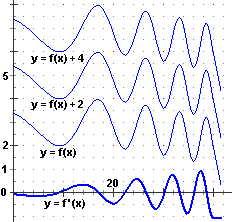
Il grafico inferiore rappresenta la funzione derivata della funzione rappresentata sopra. Il grafico superiore rappresenta una funzione primitiva della funzione rappresentata sotto.
Dal grafico della pendenza riusciamo a risalire alla forma del profilo stradale, ma non siamo in grado di stabilire l'altitudine della strada. Dovremmo conoscere almeno l'altitudine di un punto del percorso: due strade composte ciascuna da tratti in salita e in discesa uguali e con medesime pendenze, ma una in una zona vicina al mare e l'altra in una zona di montagna, hanno profili altimetrici dalla stessa forma, a cui corrispondono grafici della pendenza uguali.
Analogamente, i tre grafici sopra a destra, che sono uno ottenibile dall'altro mediante una traslazione verticale, rappresentano tre funzioni diverse che hanno la stessa funzione derivata.
Esercizio: testo e soluzione
|  |
Esempio E. Determiniamo la funzione derivata di x  x2.
x2.
Possiamo procedere come per  l'esempio D, con un generico x al posto di 1.
l'esempio D, con un generico x al posto di 1.
| lim h→0 | (x + h)2 – x2 |
| ————— |
| h |
| =
|
| lim h→0 | x2 + 2xh + h2 – x2 |
| ——————— |
| h |
| =
|
| =
|
| =
|
|
Esempio F. Determiniamo la funzione derivata di x  x3.
x3.
| lim h→0 | (x+h)3 – x3 |
| ———— |
| h |
| =
|
| lim h→0 | x3+3x2h+3xh2+h3 – x3 |
| ————————— |
| h |
| =
|
| =
|
| =
|
|
Esempio G. Determiniamo la funzione derivata di x  xn (per n intero positivo).
xn (per n intero positivo).
| lim h→0 | (x+h)n – xn |
| ———— |
| h |
| =
|
| lim h→0 | xn+nxn–1h+(…)h2 – xn |
| ————————— |
| h |
| =
|
| =
|
| =
|
|
Nello sviluppo di (x+h)n, ossia nel calcolo del prodotto tra n fattori (x+h)(x+h)…(x+h), compare la somma di n termini uguali a xn–1 h; tutti gli altri termini, a parte xn, contengono h con almeno grado 2 ( calc. combinatorio)
calc. combinatorio)
I grafici di alcune funzioni x  xn e delle loro derivate:
xn e delle loro derivate:
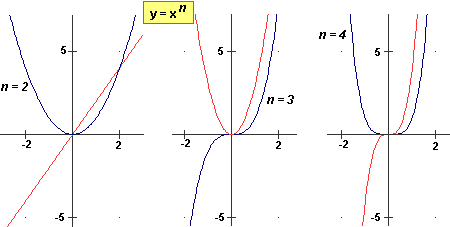
Esempio I. Determiniamo la funzione derivata di x  1/x.
1/x.
| lim h→0 | 1/(x + h) – 1/x |
| —————— |
| h |
| =
|
| lim h→0 | x – (x + h) |
| ————— |
| h(x + h)x |
| =
|
| =
|
| =
|
|
Nota. Tutti gli esempi da E ad I, ed anche quello della derivata di x → x, sono tutti casi particolari della seguente regola di derivazione (dove D indica  l'operazione di derivazione), valida per ogni numero reale α, che discuteremo in una voce successiva:
l'operazione di derivazione), valida per ogni numero reale α, che discuteremo in una voce successiva:
Dx(xα) = α xα–1
Es.: Dx(√x) = Dx(x1/2) = 1/2 x1/2–1 = 1/2 x–1/2; Dx(x–1) = –1·x–1–1 = –x–2
Esercizi: testo e soluzione
testo e soluzione
 Derivabilità e continuità
Derivabilità e continuità
I concetti di derivata e differenziale sono stati introdotti per studiare come al variare dell'input varia l'output di una funzione continua. Non è detto, comunque, che una funzione continua in un intervallo sia derivabile in tutti i punti interni ad esso.
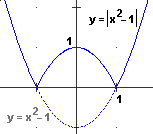
Consideriamo ad esempio la funzione x  |x| [ |x| [ funzione 1]. Per x<0 e per x>0 si comporta in entrambi i casi come una funzione lineare, a sinistra di pendenza –1, a destra di pendenza 1. Le funzioni costanti che assumono questi valori costituiscono la sua derivata in (-∞,0) funzione 1]. Per x<0 e per x>0 si comporta in entrambi i casi come una funzione lineare, a sinistra di pendenza –1, a destra di pendenza 1. Le funzioni costanti che assumono questi valori costituiscono la sua derivata in (-∞,0)  (0,∞), ma essa non è definita in 0 (per gli altri input coincide con la (0,∞), ma essa non è definita in 0 (per gli altri input coincide con la  funzione segno). funzione segno). | 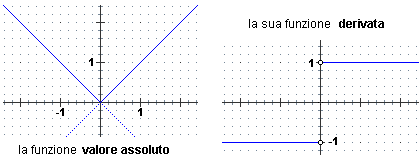 |
 |
Ecco, a sinistra, un altro esempio di funzione continua non ovunque derivabile,
con il grafico avente 2  punti angolosi;
a destra il grafico della sua derivata. punti angolosi;
a destra il grafico della sua derivata.
Oltre a casi come questi, in cui vi sono punti in cui la funzione non è derivabile in quanto ivi i limiti da destra e da sinistra delle derivate sono diversi, vi sono situazioni in cui il limite della derivata è infinito, ossia la tangente è una retta verticale,
e situazioni in cui il limite della derivata, da destra o da sinistra o da entrame le parti, non esiste, come nell'esempio di curva che presenta un punto avvicinandosi al quale aumenta la frequenza delle oscillazioni visto alla voce  lunghezza: non si sa con che direzione si arriva e con quale si riparte da esso. lunghezza: non si sa con che direzione si arriva e con quale si riparte da esso.
|  |
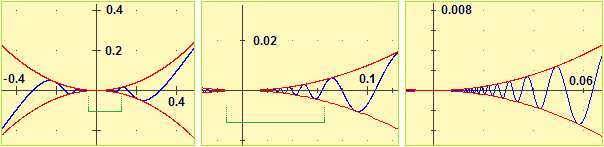
Vi sono anche situazioni come quella illustrata nella figura seguente (e discussa in uno dei successivi esercizi), in cui il grafico della funzione
avvicinandosi a un punto (l'origine) aumenta la frequenza con cui oscilla, per cui i limti da destra e da sinistra della derivata non esistono, ma
in cui esiste la tangente nel punto (nel caso illustrato si tratta dell'asse x, ossia in 0 la funzione ha derivata 0). Questo
esempio mostra che il fatto che una o entrambe le derivate da destra e da sinistra in un punto non esistono non è
sufficiente per stabilire che la derivata non esiste.
Esercizi: testo e soluzione,
testo e soluzione
 Notazioni
Notazioni
Abbiamo visto che, data una funzione f, la sua funzione derivata si indica f', dove l'apice "'" sta a indicare che si tratta di una nuova funzione rispetto a f. Ma esistono anche altre notazioni, in alcuni casi più utili di questa. Ecco le notazioni più usate per indicare la derivata di f in x (le ultime due si usano se si è convenuto di indicare f(x) con y):
| f '(x) |
( f(x) )'x |
D(f)(x) |
Dx ( f(x) ) |
|
y '(x) |
|
| (a) | (b) | (c) | (d) | (e) | (f) | (g) |
Nelle notazioni (a), (c) e (f) il segno (' o D) viene applicato al simbolo di funzione; le posso usare quando ho dato un nome alla funzione [la notazione y' a volte viene usata descrivendo  trasformazioni geometriche: dal contesto si dovrebbe essere in grado di distinguere questo impiego da quello per indicare la derivata di y(x)].
trasformazioni geometriche: dal contesto si dovrebbe essere in grado di distinguere questo impiego da quello per indicare la derivata di y(x)].
Negli altri casi occorre indicare – ad es. mettendo un x a pedice, come in (b) e (d) – qual è la variabile di input. Se non ci sono ambiguità questa indicazione può essere omessa. Le notazioni (e) e (g) sono usate anche "a 1 piano", impiegando "/".
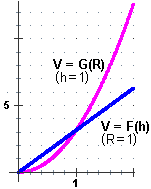 |
Ad es. se considero il volume V = πR2h di un cilindro di altezza h e raggio di base R, posso studiare come esso varia in funzione di h, considerando R costante, oppure come varia in funzione di R, pensando h costante, cioè studiare l'una o l'altra delle seguenti funzioni:
F: h  πR2h,
G: R πR2h,
G: R  πR2h πR2h
A lato sono tracciati i loro grafici per valori particolari delle costanti, ossia, fissato R in un caso, h nell'altro.
Se voglio indicare la funzione derivata di V in funzione di h è comodo usare F' o D(F). Invece V' sarebbe ambiguo (potrebbe anche essere la derivata rispetto ad R, cioè la derivata di G).
Se voglio indicare il valore generico della derivata di V in funzione di h è comodo usare F'(h), V'(h) o d V/d h, o, volendo esplicitare il termine:
|
| Se voglio indicare il valore della derivata di V in funzione di h per un particolare input, ad esempio quando h vale 2, posso usare F'(2), D(F)(2) o una delle notazioni a lato: |
Dh = 2 (πR2h) |
(πR2h)'h = 2 |
|
 La notazione d f(x) /d x può essere comodo pensarla come una abbreviazione di limΔx→0 Δf(x)/Δx, che è un modo in cui può essere riscritta la
La notazione d f(x) /d x può essere comodo pensarla come una abbreviazione di limΔx→0 Δf(x)/Δx, che è un modo in cui può essere riscritta la  espressione con cui abbiamo definito D(f):
espressione con cui abbiamo definito D(f):
sarebbe il rapporto tra Δf(x) e Δx quando questi diventano piccolissimi, "infinitesimali": d v indicherebbe una variazione infinitesimale della variabile v.
Questa è effettivamente l'idea con cui venne introdotta questa notazione (nel XVII sec., da Leibniz, circa un secolo prima delle notazioni con "'" e con "D"). Ai nostri giorni con d f(x) indichiamo il differenziale di f(x), cioè l'approssimazione di Δf(x) che si ottiene supponendo che la funzione f avvicinadosi a x sia lineare; il collegamento con l'idea precedente è questo: Δf(x) per Δx→0 (ossia quando diventa infinitesimale) tende a confondersi con d f(x).
Anche formalmente le cose tornano:
– la funzione x  x è lineare per cui dx coincide con Δx, x è lineare per cui dx coincide con Δx,
– d f(x) = f '(x) Δx,
– quindi d f(x) / dx = f '(x) Δx / Δx = f '(x). | 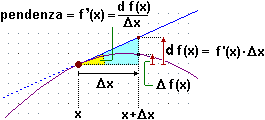 |
 Proprietà
Proprietà
Le formule seguenti, in cui f e g sono funzioni e k è un numero, presentano due proprietà di base delle derivate che facilitano il calcolo delle derivate di vari tipi di funzioni (con esse e quanto visto nell'esempio G siamo in particolare in grado di derivare tutte le funzioni polinomiali):
| D(kf) = kD(f) |
D(f+g) = D(f)+D(g) |
| Dx(k f(x)) = k Dx(f(x)) |
Dx(f(x)+g(x)) = Dx(f(x)) + Dx(g(x)) |
Ne vediamo un esempio d'uso e poi le motiviamo:
Dx(3x2 + 2√x) = Dx(3x2) + Dx(2√x) = 3Dx(x2) + 2Dx(√x) = 3·2x + 2·1/(2√x) = 6x + 1/√x
Abbiamo usato la seconda proprietà, poi la prima e, infine, quanto visto negli esempi E ed H.
La validità di queste formule è facilmente giustificabile:
• Se, al variare di x, f(x) varia di una quantità Q, allora, alla stessa variazione di x, k·f(x) varia di k·Q. In breve:
Δ(k·f(x)) = k·Δf(x). In termini geometrici: se moltiplico tutte le y per k la pendenza si molitplica per k.
• Se, al variare di x, f(x) varia di una quantità Q e g(x) varia di una quantità R, allora, alla stessa variazione di x, f(x)+g(x) varia di Q+R. In breve:
Δ((f+g)(x)) = Δf(x)+Δg(x). In termini geometrici: se sommo, in corrispondenza delle stesse x, le y dei grafici di f e di g, ottengo un grafico che man mano ha come pendenza la somma delle pendenze dei due grafici.
Vedremo altre proprietà in una voce successiva.
| Nota.
Può accadere che esista D(f+g)(x) senza che esistano
D(f)(x) e D(g)(x). Ad es. nel caso illustrato a fianco
le funzioni F e G non sono derivabili in 0 mentre la funzione somma F+G (che vale
costantemente 1) è derivabile ovunque (ha derivata che vale costantemente 0).
Come è già stato sottolineato in molte altre voci, prima di
mettersi ad usare formule, occorre riflettere e vedere se ci sono delle strade
più semplici per affrontare il problema. Di fronte alla derivazione di f(x)+g(x)
occorre vedere se è possibile trasformare in modo più semplice
l'espressione di f(x)+g(x) o se si può capire come varia
la pendenza del grafico di f+g (in modo da poter controllare gli esiti degli
eventuali calcoli successivi), prima di applicare la formula D(f+g)(x)=D(f)(x)+D(g)(x)
e tener conto che questa formula è vera nel suo dominio:
| 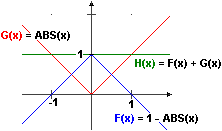 |
| per gli x per i quali D(f)(x)
e D(g)(x) non sono definiti non posso concludere nulla circa il valore o l'esistenza di D(f+g)(x). |
Esercizio: testo e soluzione
 Applicazioni: tangenti, andamento di funzioni, velocità, accelerazione
Applicazioni: tangenti, andamento di funzioni, velocità, accelerazione
Le applicazioni del concetto di derivata sono innumerevoli. In questa voce abbiamo visto come può essere usato per fare approssimazioni e calcoli approssimati (esempi  A e
A e  B). In una voce successiva si vedrà che esso consente, più in generale, di trovare
B). In una voce successiva si vedrà che esso consente, più in generale, di trovare  funzioni polinomiali per approssimare funzioni continue di qualunque tipo.
funzioni polinomiali per approssimare funzioni continue di qualunque tipo.
Abbiamo accennato ai suoi possibili impieghi per studiare limiti di funzioni (esempio  C).
C).
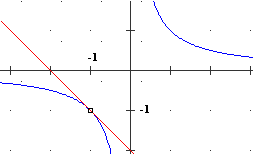
 Può essere impiegato per determinare le tangenti a una curva in un punto. Ne abbiamo accennato Può essere impiegato per determinare le tangenti a una curva in un punto. Ne abbiamo accennato  introducendo la definizione di derivata. A destra è tracciata la tangente alla curva y=1/x nel punto di ascissa -1. Per determinarla: • ne ho trovato la pendenza derivando la funzione: (1/x)' = (-1/x2) vale -1 per x=-1; • poi ho trovato la retta passante per (-1,-1) di pendenza -1: è y = -x-2. introducendo la definizione di derivata. A destra è tracciata la tangente alla curva y=1/x nel punto di ascissa -1. Per determinarla: • ne ho trovato la pendenza derivando la funzione: (1/x)' = (-1/x2) vale -1 per x=-1; • poi ho trovato la retta passante per (-1,-1) di pendenza -1: è y = -x-2.
La questione può essere approfondita a partire da un'esame della voce  rette tangenti e curve. Vediamo ad es. un modo per determinare la tangente alla curva x = t(t+1), y = t3 nel punto corrispondente a t=–1 alternativo a rette tangenti e curve. Vediamo ad es. un modo per determinare la tangente alla curva x = t(t+1), y = t3 nel punto corrispondente a t=–1 alternativo a  quello ivi considerato: quello ivi considerato:
Δy e Δx avvicinandosi al punto sono sempre meglio approssimabili con i differenziali rispetto a t dy = d(t3)dt = 3t2dt e dx = d(t(t+1))dt = d(t2+t)dt = (2t+1)dt, il cui rapporto, 3t2/(2t+1), vale –3 per t=–1. Quindi –3 è la pendenza della retta tangente.
|  |
 Il concetto di derivata, in quanto ci permette di determinare la pendenza di un grafico, ci consente di affrontare facilmente anche alcuni problemi legati all'andamento delle funzioni, sui quali torneremo. Ad es. se D(F) in un intervallo è sempre positiva, tranne che in un qualche isolato punto interno all'intervallo in cui vale 0, posso concludere che F è (strettamente) crescente nell'intervallo; è di questo tipo, ad es., x
Il concetto di derivata, in quanto ci permette di determinare la pendenza di un grafico, ci consente di affrontare facilmente anche alcuni problemi legati all'andamento delle funzioni, sui quali torneremo. Ad es. se D(F) in un intervallo è sempre positiva, tranne che in un qualche isolato punto interno all'intervallo in cui vale 0, posso concludere che F è (strettamente) crescente nell'intervallo; è di questo tipo, ad es., x  x3, che ha 3x2 come derivata in x: questa è sempre positiva, tranne che per x=0 quando vale 0 (ciò corrisponde ad un grafico - riprodotto
x3, che ha 3x2 come derivata in x: questa è sempre positiva, tranne che per x=0 quando vale 0 (ciò corrisponde ad un grafico - riprodotto  in una delle precedenti figure - che ha pendenza sempre positiva, tranne che nell'origine in cui ha tangente orizzontale).
in una delle precedenti figure - che ha pendenza sempre positiva, tranne che nell'origine in cui ha tangente orizzontale).
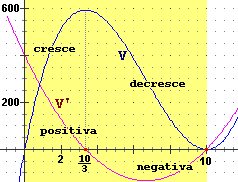 |
Per fare un esempio concreto rivediamo il problema si rendere massimo il volume V = (20-2x)2x di una scatola alta x cm da realizzare con un quadrato di lamiera di lato 20 cm, considerato alla voce  risoluz. equazioni 2. Là con un metodo grafico viene trovata come soluzione x = 3.33. Ora, disponendo del concetto di derivazione, possiamo fare: risoluz. equazioni 2. Là con un metodo grafico viene trovata come soluzione x = 3.33. Ora, disponendo del concetto di derivazione, possiamo fare:
V' = D((20-2x)2x) = D(4x3-80x2+400x) = 12x2-160x+400 e studiare il segno di V', ovvero, dividendo per 4, sudiare il segno di 3x2-40x+100.
Questa è una funzione quadratica con coefficiente direttivo positivo che si annulla in
40/6-√(1600-1200)/6 e in 40/6+√(1600-1200)/6, ossia in 10/3 e in 10.
Ciò ci consente di concludere (vedi figura a lato) che V cresce per x ≤ 10/3 e decresce per 10/3 ≤ x ≤ 10.
Quindi, nell'intervallo [0,10] che ci interessa (quello in cui può variare l'altezza della scatola),
V assume valore massimo quando x = 10/3 = 3.333…, valore che, poi,
dobbiamo approssimare tenendo conto del contesto del problema. |
|
Nota. Una funzione che in un intorno del valore m assuma valore massimo in
m stesso si dice che ha ivi un massimo
relativo, nel senso che, al di fuori di tale intervallo, potrebbe assumere valori maggiori che in m. Analogamente si dice che
ha la funzione ha un minimmo
relativo in m se ivi assume il valore minimo rispetto ad un intervallo centrato in tale valore. Se si vuole evidenziare
che un tale punto,
oltre ad essere di minimo o di massimo relativo, è un massimo o minimo nell'intero dominio della funzione, si parla anche di
massimo o di minimo assoluto. I problemi di ricerca del massimo o del minimo di una
funzione sono chiamati anche problemi di ottimizzazione e, per le applicazioni
che hanno in ambito economico e tecnologico, sono uno dei settori della matematica applicata
più usati. |
In modo analogo posso determinare i vertici delle parabole, con un procedimento più semplice di quello algebrico ( funz. polinomiali):
il vertice di y = 4x2 + 12x – 1 ha x tale che Dx(4x2+12x–1)=0, ossia 8x+12=0, ossia x=-3/2;
la y del vertice è 9–18–1 = -10; il vertice è (-3/2,-10). funz. polinomiali):
il vertice di y = 4x2 + 12x – 1 ha x tale che Dx(4x2+12x–1)=0, ossia 8x+12=0, ossia x=-3/2;
la y del vertice è 9–18–1 = -10; il vertice è (-3/2,-10).
Nel caso di una generica parabola y = ax2 + bx + c ho: Dx(ax2+bx+c) = 2ax+b = 0 per x = –b/(2a). |
Esercizio: testo e soluzione
 Infine, la derivata consente di esprimere la velocità di variazione di una grandezza.
Infine, la derivata consente di esprimere la velocità di variazione di una grandezza.
Pensiamo al caso in cui P(t) sia la posizione lungo una autostrada in cui si trova all'ora t un mezzo che viaggia a velocità costante. In questo caso P(t) varia proporzionalmente alla variazione di t: se raddoppia il tempo trascorso raddoppia la strada percorsa) e ΔP(t)/Δt, ossia il rapporto tra la strada percorsa e il tempo impiegato, esprime la velocità del mezzo. Ad es., se la posizione è espressa chilometricamente e il tempo in ore, ΔP(t)/Δt = 115 indica che il mezzo viaggia a 115 km/h.
Se il mezzo non ha velocità costante possiamo approssimare la velocità che ha all'istante t calcolando ΔP(t)/Δt per una piccola variazione di tempo. Ad esempio se per Δt = 1/60, ossia al passare di 1 min, la posizione lungo la strada ha subito la variazione ΔP(t) = 2, allora ΔP(t)/Δt = 120: il mezzo viaggia a circa 120 km/h; questa sarebbe esattamente la sua velocità se in questo intervallo di tempo non avesse accelerato o decelerato.
La velocità all'istante t non è altro che limΔt→0ΔP(t)/Δt, ossia P'(t).
Questa formula non è altro che la sintesi del procedimento che puoi trovare sviluppato più estesamente alla voce  velocità di variazione.
velocità di variazione.
Potremmo anche ragionare in termini di  variazione tendenziale, come fatto all'inizio di questa voce:
variazione tendenziale, come fatto all'inizio di questa voce:
la velocità all'istante t non è altro che il rapporto tra la variazione tendenziale dP(t) della posizione lungo la strada del mezzo (di quanto si sposterebbe se mantenesse la stessa andatura) e la variazione Δt del tempo, che  non è altro che P'(t).
non è altro che P'(t).
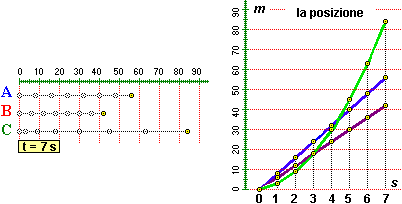
• Vediamo, in breve, un esempio discusso alla voce  velocità di variazione. Tre mezzi avanzano nel modo raffigurato sotto a sinistra, mediante foto scattate ad intervalli di 1 secondo. A destra la loro posizione x (in m) in funzione del tempo t (in s) è descritta anche mediante formule. A e B hanno velocità costante, C sta accelerando, ossia ha velocità crescente. Per quanto ora visto, le loro velocità (in m/s) sono:
velocità di variazione. Tre mezzi avanzano nel modo raffigurato sotto a sinistra, mediante foto scattate ad intervalli di 1 secondo. A destra la loro posizione x (in m) in funzione del tempo t (in s) è descritta anche mediante formule. A e B hanno velocità costante, C sta accelerando, ossia ha velocità crescente. Per quanto ora visto, le loro velocità (in m/s) sono:
|
vA(t) = D(6t) = 6 | vB(t) = D(8t) = 8 | vC(t) = D(1.5t2 + 1.5t) = 3t + 1.5
|
Geometricamente, nei primi due casi 6 e 8 corrispondono alla pendenza costante dei grafici di x in funzione di t, nel terzo caso 3t+1.5 indica come varia la pendenza al trascorrere del tempo.
Per valutare come varia la velocità di C al passare del tempo possiamo a sua volta derivare vC(t):
accelerazione di C = Dt(vC(t)) = Dt(3t + 1.5) = 3
Il mezzo C sta avanzando con accelerazione costante: la sua velocità aumenta di 3 m/s ogni secondo, ossia di 3 m/s/s = 3 m/s2.
• Un esempio in cui la velocità di variazione non è rispetto al tempo:
qual è la velocità con cui cresce il volume V di un cubo al crescere del lato l? e l'accelerazione?
V = l 3; d V / d l = 3 l 2: velocità;
d 3 l 2 / d l = 6 l : accelerazione (anche l'accelerazione in questo caso è crescente).
 I vettori velocità e accelerazione (e forza)
I vettori velocità e accelerazione (e forza)
Negli esempi precedenti abbiamo esaminato il movimento di un mezzo considerando la strada percorsa senza prendere in considerazione la traiettoria, cioè i cambiamenti di direzione. La velocità di cui abbiamo parlato finora l'abbiamo intesa come grandezza scalare, non vettoriale [ vettori]. vettori].
|
Il concetto di derivata consente di definire anche il vettore velocità:
– mediante il calcolo della tangente ci fornisce la direzione della velocità,
– mediante il calcolo della rapidità della variazione della posizione ce ne fornisce l'intensità.
Vediamo come si può determinare il vettore velocità nel caso del moto curvilineo seguente,
che a lato è rappresentato in forma animata per t (inteso qui come tempo in secondi) che varia da 0 a 4 (si tratta di istantanee scattate ogni 1/2 secondo)
[vedi qui se vuoi tracciare la curva con R]:
x(t) = t2 – 5t + 5, y(t) = t2 – 3.
Dalla animazione capiamo che il mezzo rallenta entrando nella curva (i pallini si avvicinano) e poi accelera (i pallinini si diradano). Controlleremo poi se i conti sono in accordo con questa nostra intuizione.
• Per trovare la direzione della velocità basta trovare la tangente, abbiamo già visto come
( facendo il rapporto tra i differenziali rispetto a t): facendo il rapporto tra i differenziali rispetto a t):
dy/dx = 2t/(2t–5)
Inizialmente (t=0) abbiamo dy/dx = 0, in accordo con quanto si vede a lato (inizialmente la direzione è orizzontale); dopo 1" (t=1) dy/dx = –-2/3 (nel terzo pallino la tangente ha pendenza negativa); dopo 4" dy/dx = 8/3 (nell'ultimo pallino la direzione è lungo una retta con pendenza positiva). | 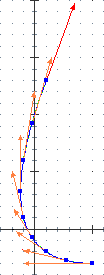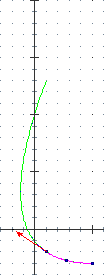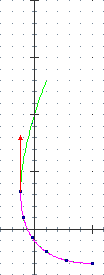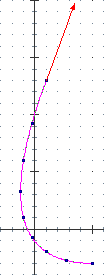 |
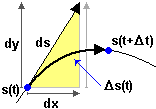 |
• Per trovare la intensità della velocità, se indico con s(t) la posizione lungo la strada e con Δs la distanza lungo la strada percorsa nel tempo Δt, devo fare limΔt→0Δs/Δt.
Per Δt→0 posso approssimiare la strada percorsa Δs con la strada ds che si "tenderebbe" a percorrere se sia lungo la direzione x che lungo la direzione y si proseguisse con le variazioni tendenziali, ossia quelle date dai differenziali:
ds = √((dx)2+(dy)2) =
√(((2t–5)dt)2 + ((2t)dt)2) = dt√(8t2–20t+25).
Quindi: ds/dt = √(8t2–20t+25).
Inizialmente ds/dt = 5, per t=1 ds/dt = √13 = 3.6, per t=4 ds/dt = √73 = 8.5, in accordo con le nostre considerazioni intutive iniziali.
|
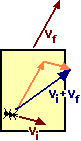
• In alternativa (vedi figura a lato in cui sono evidenziati due particolari istanti del moto considerato sopra) posso considerare separatamente la velocità in orizzontale, vx, e quella in verticale, vy.
Nel primo istante la velocità verticale è nulla per cui la velocità coincide con quella orizzontale. Nell'altro istante la velocità è la somma dei vettori vx e vy.
Le velocità in orizzontale e in verticale non sono altro che le derivate x'(t) e y'(t) di x e di y rispetto a t, per cui il vettore velocità è: (x'(t), y'(t))
A partire da ciò ritrovo gli stessi risultati; ad esempio nel caso del movimento sopra considerato ottengo che la velocità è il vettore (2t-5, 2t), la cui pendenza è 2t/(2t-5) e la cui intensità è √((2t–5)2 + (2t)2) = √(8t2–20t+25).
Questa formulazione del concetto di velocità ci permette far vedere facilmente che si tratta effettivamente di una grandezza vettoriale [ vettori], cioè che la velocità di moti composti, come quelle considerati alla voce vettori], cioè che la velocità di moti composti, come quelle considerati alla voce  rette tangenti e curve.(barca che si muove in un canale con acqua in movimento, …), è pari alla somma di quelle dei singoli moti. rette tangenti e curve.(barca che si muove in un canale con acqua in movimento, …), è pari alla somma di quelle dei singoli moti. | 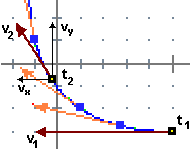 |
Consideriamo, infatti, un oggetto sottoposto a due movimenti, come l'insetto raffigurato a fianco, che:
- si muove su un foglio con xi = 2t, yi = -t (coordinate in mm, t in s),
- il quale foglio a sua volta si muove sul pavimento con xf = t2, yf = 4t.
Il suo moto complessivo è x = xi+xf , y = yi+yf e la sua velocità è il vettore (x'(t)), y'(t)), che, per la proprietà D(f+g) = D(f)+D(g), è pari a (x'i(t)+x'f(t), y'i(t)+y'f(t)), che è pari a (x'i(t), y'i(t))+(x'f(t), y'f(t)), ossia alla somma delle velocità vi e vf di insetto rispetto al foglio e di foglio rispetto al pavimento:
vi = (2,-1) (2 mm/s a destra, 1 mm/s in giù), vf = (2t,4) (velocità crescente a destra, 4 mm/s in su); vi+vf = (2+2t, 3).
|  |
Va sottolineato che il concetto di velocità media che abbiamo presentato nella voce
 valori medi - 1 era
riferito alla velocità scalare. In particolare un oggetto che abbia velocità media eguale in ogni intervallo, ovvero che
percorra a parità di tempo sempre la stessa quantità di strada, non è detto che abbia una velocità
con intensità costante. Se un'auto mantiene la velocità di 60 km/h in un tratto prima rettilineo, poi in una curva e, infine,
in un successivo tratto rettilineo, nel momento in cui cambia direzione mantiene costante, pari a 60 km/h, la velocità tangenziale
(ossia la componente della velocità via via diretta come la tangente alla strada) ma ha anche una componente della velocità centripeta,
ossia diretta via via verso il centro dell'arco di cerchio che l'auto sta percorrendo, che, appunto, corrisponde al cambiamento di direzione.
valori medi - 1 era
riferito alla velocità scalare. In particolare un oggetto che abbia velocità media eguale in ogni intervallo, ovvero che
percorra a parità di tempo sempre la stessa quantità di strada, non è detto che abbia una velocità
con intensità costante. Se un'auto mantiene la velocità di 60 km/h in un tratto prima rettilineo, poi in una curva e, infine,
in un successivo tratto rettilineo, nel momento in cui cambia direzione mantiene costante, pari a 60 km/h, la velocità tangenziale
(ossia la componente della velocità via via diretta come la tangente alla strada) ma ha anche una componente della velocità centripeta,
ossia diretta via via verso il centro dell'arco di cerchio che l'auto sta percorrendo, che, appunto, corrisponde al cambiamento di direzione.
 Lo studio dei
movimenti e dei fattori fisici che li governano è affrontato da un ramo della fisica chiamato dinamica
(nome derivato dal greco dinamis, forza); è una branca della meccanica (che si occupa del funzionamento
dei meccanismi; di quello dei motori si occupano altri rami della fisica, come l'elettromagnetismo – motori
elettrici - e la termodinamica – motori a carburante). I personaggi che, più di ogni altro, sono all'origine dello
sviluppo della dinamica sono l'italiano Galileo Galilei (1564-1642), i francesi René Descartes (1596-1650), spesso
italianizzato in "Cartesio", e Pierre de Fermat (1601-1665), l'inglese Isaac Newton (1643-1727).
Lo studio dei
movimenti e dei fattori fisici che li governano è affrontato da un ramo della fisica chiamato dinamica
(nome derivato dal greco dinamis, forza); è una branca della meccanica (che si occupa del funzionamento
dei meccanismi; di quello dei motori si occupano altri rami della fisica, come l'elettromagnetismo – motori
elettrici - e la termodinamica – motori a carburante). I personaggi che, più di ogni altro, sono all'origine dello
sviluppo della dinamica sono l'italiano Galileo Galilei (1564-1642), i francesi René Descartes (1596-1650), spesso
italianizzato in "Cartesio", e Pierre de Fermat (1601-1665), l'inglese Isaac Newton (1643-1727).
Galileo formulò il principio d'inerzia, secondo il quale un corpo
cambia velocità solo se su di esso agisce una forza ("inerzia" indica lo stato di chi non modifica il proprio
comportamento). Prima di lui, ingannati dal fatto che un oggetto in movimento tende a fermarsi se non viene continuamente
spinto o tirato, si riteneva che per mantenere un corpo in movimento occorresse esercitare su di esso una forza.
Galileo intuì che, invece, era il rallentamento del corpo ad essere causato dall'intervento di forze (attrito,
resistenza dell'aria, …), e confermò questa sua tesi analizzando matematicamente gli esiti di una serie
di esperimenti in cui cercò di ridurre l'incidenza delle forze frenanti.
Galileo mise a punto anche un modello matematico per il movimento dei corpi che cadono.
La novità introdotta da Galileo fu proprio lo studio dei fenomeni attraverso gli esperimenti e la loro rappresentazione mediante leggi matematiche generali,
rompendo con la tradizione aristotelica, secondo la quale i fenomeni erano studiati su una base teologica e filosofica (e aprendo collegamenti tra la "scienza" e la "tecnica", che
fino ad allora elaborava le proprie conoscenze su base empirica). Vedi.
Un ruolo fondamentale per i successivi sviluppi lo ha avuto la matematizzazione del
concetto di  spazio mediante
le coordinate, con la conseguente possibilità di descrivere curve mediante equazioni.
Questa rappresentazione numerica dello spazio è dovuta a Descartes,
dal cui nome deriva la parola "coordinate cartesiane", e a Fermat, a cui si devono anche le
prime formulazioni del rapporto incrementale.
spazio mediante
le coordinate, con la conseguente possibilità di descrivere curve mediante equazioni.
Questa rappresentazione numerica dello spazio è dovuta a Descartes,
dal cui nome deriva la parola "coordinate cartesiane", e a Fermat, a cui si devono anche le
prime formulazioni del rapporto incrementale.
Newton mise, infine, a punto un modello matematico generale dell'origine dei movimenti introducendo il concetto di derivata per descrivere matematicamente la velocità (come derivata dello spostamento) e la accelerazione (come derivata della velocità):
un corpo soggetto complessivamente a una forza F si muove con una accelerazione avente la stessa direzione di F e intensità proporzionale all'intensità di F e alla propria massa.
In seguito al principio formulato da Newton, il concetto di forza è stato precisato ed espresso come prodotto m·a tra l'accelerazione a che essa è in grado di imprimere ad un corpo e la massa m di esso.
E ha preso il nome Newton (N) la sua unità di misura: 1 N = 1 kg·m/s2 [ vettori]. Accanto a Newton, lo sviluppo del concetto di derivata
è dovuto a Leibniz (vedi).
vettori]. Accanto a Newton, lo sviluppo del concetto di derivata
è dovuto a Leibniz (vedi).
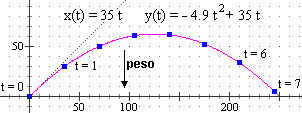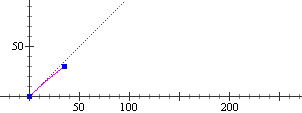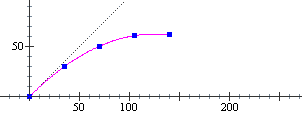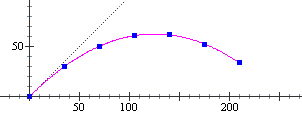
 Prendiamo in esame il lancio di un oggetto. Consideriamo una freccia o una bilia metallica, in modo che sia trascurabile l'attrito con l'aria. Supponiamo di lanciarla con una inclinazione di 45°, con una velocità tale che avanzi di 35 m/s e si innalzi di 35 m/s, ossia che che si muova nella direzione 45° con la velocità di √(352+352) m/s = 49.50 m/s (approssimando al cm/s).
Se non ci fosse la forza di gravitazione che attira l'oggetto verso terra (peso), esso continuerebbe a procedere nella direzione 45°, con la stessa velocità. La presenza della forza peso, diretta verticalmente verso il basso, frena la salita, ma non ostacola l'avanzamento orizzontale, come si vede nella figura sottostante, in cui si è preso l'asse x diretto come l'avanzamento orizzontale: ad ogni secondo la x dell'oggetto aumenta di 35 (dopo 7 s è avanzato di 7·35 = 49·5 = 490/2 = 245 m).
Prendiamo in esame il lancio di un oggetto. Consideriamo una freccia o una bilia metallica, in modo che sia trascurabile l'attrito con l'aria. Supponiamo di lanciarla con una inclinazione di 45°, con una velocità tale che avanzi di 35 m/s e si innalzi di 35 m/s, ossia che che si muova nella direzione 45° con la velocità di √(352+352) m/s = 49.50 m/s (approssimando al cm/s).
Se non ci fosse la forza di gravitazione che attira l'oggetto verso terra (peso), esso continuerebbe a procedere nella direzione 45°, con la stessa velocità. La presenza della forza peso, diretta verticalmente verso il basso, frena la salita, ma non ostacola l'avanzamento orizzontale, come si vede nella figura sottostante, in cui si è preso l'asse x diretto come l'avanzamento orizzontale: ad ogni secondo la x dell'oggetto aumenta di 35 (dopo 7 s è avanzato di 7·35 = 49·5 = 490/2 = 245 m).

Mentre il vettore velocità dell'oggetto è man mano diretto tangenzialmente alla traiettoria,
l'accelerazione in questo caso è sempre diretta verticalmente e verso il basso; ciò è la traduzione di quanto detto sopra: l'oggetto avanza orizontalmente con la stessa velocità ma si alza con velocità man mano minore, fino a diventare nulla quando l'oggetto raggiunge la massima altezza, dopo di che la velocità verticale cambia direzione, e l'oggetto incomincia a scendere.
L'accelerazione in questo caso è quella di gravità, che [ vettori] alla nostra latitudine, al livello del mare, è 9.80±0.01 m/s2.
È facile dedurre che il moto del nostro oggetto è descritto dalle equazioni riportate in figura, cioè (considerndo x e y in metri e t in secondi) da: x = 35 t, y = – 4.9 t2 + 35 t.
vettori] alla nostra latitudine, al livello del mare, è 9.80±0.01 m/s2.
È facile dedurre che il moto del nostro oggetto è descritto dalle equazioni riportate in figura, cioè (considerndo x e y in metri e t in secondi) da: x = 35 t, y = – 4.9 t2 + 35 t.
Infatti il vettore velocità (in m/s) è:
(x'(t), y'(t)) = (35, – 4.9·2 t2 – 1 + 35) = (35, – 9.8 t + 35)
la cui velocità di variazione, ossia il vettore accelerazione (in m/s2), è:
( D(35), D(–9.8 t + 35) ) = (0, –9.8)
che ha come intensità 9.8 m/s2 e direzione verticale in basso (la componente orizzontale è 0 e quella verticale è negativa): è proprio l'accelerazione di gravità.
La traiettoria dell'oggetto lanciato è una parabola, infatti da x = 35 t AND y = – 4.9 t2 + 35 t si ricava t = x/35 e, quindi, y = – 4.9 (x/35)2 + 35x/35, ossia y = –0.004x2+x.
E il "proiettile" arriva nel punto x (diverso da 0) in cui y = 0, ossia quando –0.004x2+x = (–0.004x+1)x = 0, cioè quando x = 1/0.004 = 1000/4 = 250 (metri), come si vede anche dalla figura.
Vediamo com'è l'accelerazione nel caso del moto x(t) = t2 – 5t + 5, y(t) = t2 – 3 considerato  sopra.
Abbiamo già visto che la velocità è il vettore (D(t2–5t+5), D(t2 – 3)) = (2t–5, 2t).
Il vettore accelerazione è dunque: (D(2t–5), D(2t)) = (2, 2)
(2 m/s2 sia in direzione x che in direzione y, ossia inclinazione di 45° rispetto asse x e intensità
√(22+22) = √(2·22) = 2√2 m/s2). sopra.
Abbiamo già visto che la velocità è il vettore (D(t2–5t+5), D(t2 – 3)) = (2t–5, 2t).
Il vettore accelerazione è dunque: (D(2t–5), D(2t)) = (2, 2)
(2 m/s2 sia in direzione x che in direzione y, ossia inclinazione di 45° rispetto asse x e intensità
√(22+22) = √(2·22) = 2√2 m/s2).
Dunque anche in questo caso il corpo è soggetto a una accelerazione costante, diretta non verticalmente ma inclinata di 45°. In altre parole il corpo in movimento è soggetto a una forza costante diretta come indicato nella figura qui a destra.
Possiamo anche concludere che la traiettoria è una parabola con asse di simmetria inclinato di 45°.
Qual è il vertice di essa? È il punto in cui la tangente è perpendicolare all'asse di simmetria.
L'asse ha pendenza 2/2 = 1. La tangente ha la pendenza del vettore velocità, (2t)/(2t–5). Dobbiamo trovare per quale t essa e la pendenza dell'asse sono una il reciproco dell'altra cambiato di segno:
(2t–5)/(2t) = –1 <=> 2t–5 = –2t <=> 4t = 5 <=> t = 5/4
Si tratta quindi del punto: x = (5/4)2–5·5/4+5 = 5/16 = 0.3125, y = (5/4)2–3 = –23/16 = –1.4375.
Consideriamo, infine, un mezzo che si muove lungo una traiettoria circolare.
|  |
 |
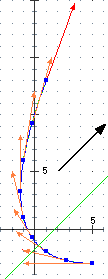
Nella figura più a sinistra è illustrato il caso di un mezzo che si muove con velocità di intensità costante: il vettore velocità cambia direzione ma ha sempre la stessa lunghezza.
È come il moto di un satellite in orbita circolare attorno alla Terra. La sua accelerazione è diretta come la forza che lo attira verso la Terra.
Nel caso raffigurato a destra invece il mezzo si muove con velocità di intensità crescente. Potrebbe essere un'automobilina telecomandata legata ad un filo fissato al terreno:
la forza impressa dal motorino la fa andare via via più velocemente, la forza esercitata dal filo le impedisce di proseguire lungo una retta.
La prima forza è diretta tangenzialmente, la seconda verso il centro di rotazione;
la loro somma è una forza che punta un po' più avanti del centro di rotazione.
Il vettore accelerazione, rappresentato in figura, è diretto come questa forza; sono raffigurate anche le sue componenti tangenziale e centrale,
corrispondenti alle due componenti della forza.
|
 L'area della matematica che si occupa dello studio delle proprietà e delle applicazioni del concetto di derivata si chiama calcolo differenziale. L'area più generale che si occupa delle funzioni a (uno o più) input e output reali (o
L'area della matematica che si occupa dello studio delle proprietà e delle applicazioni del concetto di derivata si chiama calcolo differenziale. L'area più generale che si occupa delle funzioni a (uno o più) input e output reali (o  complessi), del concetto di limite e degli altri concetti ad esso collegati (oltre alle derivate, i metodi per calcolare lunghezze, aree e volumi di figure definite mediante funzioni od equazioni, le proprietà delle funzioni continue, …) viene chiamata analisi matematica. Spesso l'aggettivo analitico, in matematica, viene usato per indicare metodi in cui un oggetto o una proprietà viene studiata usando tecniche di analisi matematica. In particolare lo studio delle figure mediante il ricorso alle funzioni od equazioni che le hanno per grafici viene a volte chiamato geometria analitica (è una terminologia introdotta nei primi anni del XIX secolo per distinguerla dall'approccio alla geometria allora più diffuso, in cui lo studio delle figure era basato su metodi, più direttamente legati alla immediata intuizione fisica, che non ricorrevano ai numeri reali e alle funzioni).
complessi), del concetto di limite e degli altri concetti ad esso collegati (oltre alle derivate, i metodi per calcolare lunghezze, aree e volumi di figure definite mediante funzioni od equazioni, le proprietà delle funzioni continue, …) viene chiamata analisi matematica. Spesso l'aggettivo analitico, in matematica, viene usato per indicare metodi in cui un oggetto o una proprietà viene studiata usando tecniche di analisi matematica. In particolare lo studio delle figure mediante il ricorso alle funzioni od equazioni che le hanno per grafici viene a volte chiamato geometria analitica (è una terminologia introdotta nei primi anni del XIX secolo per distinguerla dall'approccio alla geometria allora più diffuso, in cui lo studio delle figure era basato su metodi, più direttamente legati alla immediata intuizione fisica, che non ricorrevano ai numeri reali e alle funzioni).
 Qui trovi come
calcolare le derivate delle funzioni col programma R.
Qui trovi come
calcolare le derivate delle funzioni col programma R.
Esercizi: testo e soluzione; testo e soluzione; testo e soluzione; testo e soluzione.
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 pendenza 2,
pendenza 2,  rette tangenti e curve e
rette tangenti e curve e  velocità di variazione vengono proposte diverse situazioni e idee che motivano e introducono il concetto di derivata, uno dei più importanti della matematica. Esamina almeno una di tali voci prima di intraprendere la lettura di questa.
In alternativa, per una presentazione più sintetica, guarda direttamente la scheda La derivazione di funzioni
velocità di variazione vengono proposte diverse situazioni e idee che motivano e introducono il concetto di derivata, uno dei più importanti della matematica. Esamina almeno una di tali voci prima di intraprendere la lettura di questa.
In alternativa, per una presentazione più sintetica, guarda direttamente la scheda La derivazione di funzioni
 qui
qui


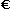

 √x si può trovare (vedremo come
√x si può trovare (vedremo come 
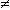 1 i due termini sono equivalenti, e quindi hanno lo stesso comportamento per x→1. Potevo operare anche trasformando, con un procedimento inverso alla razionalizzazione [
1 i due termini sono equivalenti, e quindi hanno lo stesso comportamento per x→1. Potevo operare anche trasformando, con un procedimento inverso alla razionalizzazione [




 (0,∞),
(0,∞),