Note. Nelle applicazioni, quando le direzioni sono espresse senza usare i
gradi, spesso si aggiunge il termine radianti
(simbolo: rad): si parla di «π rad, π/2
rad, …». È una aggiunta non necessaria, ma
spesso comoda. La scrittura sin(30) non indica il seno di 30 gradi,
per il quale occorre scrivere sin(30°).
In alcuni ambiti tecnici particolari si usa il grado centesimale, ossia l'unità di misura
degli angoli corrispondnete alla centesima parte di un angolo retto; il suo simbolo è
gon. Il alcune calcolatrici viene usato grad. Quindi π/2 = 90° = 100 gon (in qualche libro di scuola per geometri
si trova scritto sin(50) al posto di sin(50 gon), per indicare sin(π/4); è un
grave errore!).
In  Rappresentazione
sessagesimale dei numeri abbiamo visto come, accanto a scritture come 27.335° (chiamate a volte "sessadecimali"),
si impiegano scritture sessagesimali come 27°20'06". Rappresentazione
sessagesimale dei numeri abbiamo visto come, accanto a scritture come 27.335° (chiamate a volte "sessadecimali"),
si impiegano scritture sessagesimali come 27°20'06".
|
Notiamo che in alcuni libri scolastici per geometri si usano, erroneamente, scritture come sin(30°) e
sin(−30°) per indicare sin(90°−30°) e sin(90°+30°). È uno strano abuso (che renderà
difficile lo studio a chi proseguisse gli studi a livello universitario o a chi usasse una calcolatrice
scientifica o un qualunque software o un qualunque manuale di tipo scientifico o … a chi esaminasse un buon manuale
di topografia) frutto della grossolana confusione tra il concetto di angolo usato come input della funzione seno e
l'angolo zenitale, che è, appunto, pari a π/2−x se x è l'angolo formato
con il piano orizzontale. |
 |
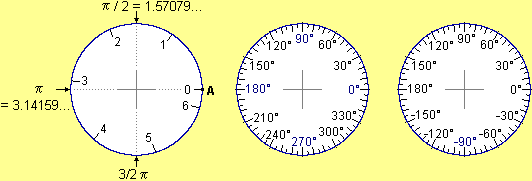
 In
molti casi (→ figura sopra a destra) come insieme delle direzioni si considera non
[0°,360°), ma (–180°,180°] o [–180°,180°).
Si possono fare anche altre scelte. Comunque, quando si scrive
–90° si intende la stessa direzione di quando si scrive
270°. In
molti casi (→ figura sopra a destra) come insieme delle direzioni si considera non
[0°,360°), ma (–180°,180°] o [–180°,180°).
Si possono fare anche altre scelte. Comunque, quando si scrive
–90° si intende la stessa direzione di quando si scrive
270°.
Più
in generale si può dire che due numeri x e y indicano la
stessa direzione (sono uguali come direzioni) se
sono lo stesso numero o se uno è ottenibile dall'altro
aggiungendo o togliendo ripetutamente 360° (cioè se esiste un numero intero k tale che x = y + k·360°, ovvero, poiché 360°=2π, x = y + 2kπ.
 Le funzioni Le funzioni  coseno e seno
vengono dette funzioni circolari in quanto [ coseno e seno
vengono dette funzioni circolari in quanto [ figura iniziale]
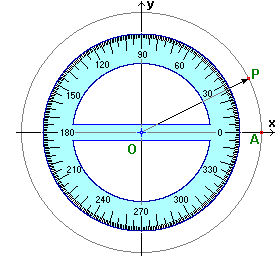
esprimono le coordinate di un punto P sul cerchio di centro
O e raggio 1, se si dà in input la direzione α del vettore OP (il cerchio di centro O e raggio 1, in quanto usato per simulare un figura iniziale]
esprimono le coordinate di un punto P sul cerchio di centro
O e raggio 1, se si dà in input la direzione α del vettore OP (il cerchio di centro O e raggio 1, in quanto usato per simulare un  goniometro, viene chiamato a volte cerchio goniometrico e,
di conseguenza, le funzioni circolari sono chiamate anche funzioni goniometriche, o trigonometriche, per infilarci anche un po' della parola "triangolo"). goniometro, viene chiamato a volte cerchio goniometrico e,
di conseguenza, le funzioni circolari sono chiamate anche funzioni goniometriche, o trigonometriche, per infilarci anche un po' della parola "triangolo").
L'essere sin(α) e cos(α) le coordinate di un punto del cerchio x2+y2=1 corrisponde al fatto
che ne verificano l'equazione, ossia che vale la relazione sin(α)2 + cos(α)2 = 1.
Un'altra funzione circolare è la
funzione tangente, che ad α
associa la pendenza del vettore OP, cioè yP/xP [ pendenze e curve di livello]. pendenze e curve di livello].
La tangente di α
viene indicata tan(α).
Evidentemente equivale a sin(α)/cos(α).
Nota. Accanto alle notazioni sin(x), cos(x) e tan(x) sono impiegate le notazioni sin x, cos x e tan x.
Sono notazioni "abbreviate" e usate con convenzioni diverse dalle usuali, e in cui va opportunamente interpretato il ruolo degli spazi bianchi. Ecco alcuni esempi:
| notazione standard | nei linguaggi di programmaz. | notazione abbreviata |
| sin(2x) | sin(2*x) | sin 2x |
| sin(x)2 | sin(x)^2 | sin2 x |
| sin(x2) | sin(x^2) | sin x2 |
| sin(x)·cos(x) | sin(x)*cos(x) | sin x cos x |
|
|
Se si adotta la notazione abbreviata è bene non impiegarla nei casi ambigui.
Ad esempio mentre è chiaro che sin √x, sin x2
e il termine a sinistra equivalgono a sin(√x), sin(x2) e
sin(x/y), nel caso di sin xy e
di sin x/y è meglio usare
sin(xy) o sin(x)y,
sin(x/y) o sin(x)/y a seconda
di quale sia il termine a cui ci si vuole riferire.
|
| F(x2) e F(x)2 indicano, rispettivamente,
F(x·x) e F(x)·F(x).
Analogamente sin(3x)2 equivale a
sin(3x)^2, ovvero a sin(3x)·sin(3x). Usando la "notazione abbreviata"
si potrebbe intendere che
sin (3x)2 (con uno spazio bianco tra sin e la coppia
di parentesi) stia per sin((3x)2);
ci sono persone che usano questa scrittura ed erroneamente omettono lo spazio bianco tra sin e (3x)2;
di fronte a scritture di questo tipo è bene chiedere agli autori (o capire dal contesto) a quale termine
intendono riferirsi. Tutti i programmi e il software matematico interpretano correttamente
sin(3*x)^2 come sin(3x)·sin(3x) e accettano come
sin((3x)2) la scrittura sin((3*x)^2)
|
 Le CT permettono di
calcolare le funzioni circolari mediante i tasti Le CT permettono di
calcolare le funzioni circolari mediante i tasti 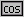 , ,  e e  . .
In
genere le CT, al loro avvio, sono predisposte per operare in gradi.
Con appositi tasti si può passare alla rappresentazione in
radianti (o anche in "gradi centesimali": 1 grado centesimanle = π/100).
Le sequenze di tasti
  (o
(o 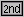  ), ),
  e
e   calcolano le funzioni inverse delle funzioni
circolari, o, meglio, dato in input un numero, restituiscono una
delle direzioni che ha tale valore come, rispettivamente, tangente
(pendenza), coseno e seno:
calcolano le funzioni inverse delle funzioni
circolari, o, meglio, dato in input un numero, restituiscono una
delle direzioni che ha tale valore come, rispettivamente, tangente
(pendenza), coseno e seno:
ad esempio, se batto 1   ottengo come output 45°, ma anche 125° (= 45° + 180°) ha
pendenza 1.
ottengo come output 45°, ma anche 125° (= 45° + 180°) ha
pendenza 1.
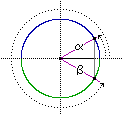 |  | 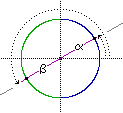 |
β = 360° - α [= - α]
α e β individuano sul cerchio
la stessa x, cioè
cos(α) = cos(β)
ma x  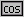 dà solo α dà solo α |
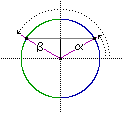
β = 180° - α
α e β individuano sul cerchio
la stessa y, cioè
sin(α) = sin(β)
ma y  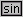 dà solo α dà solo α |
β = 180° + α
α e β hanno la stessa
pendenza p, cioè
tan(α) = tan(β)
ma p   dà solo α dà solo α |
|
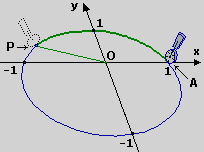
Per trovare la direzione del vettore (2,1) considerato nel  primo esempio posso calcolarne la pendenza e poi fare l'inversa della tangente: 1 primo esempio posso calcolarne la pendenza e poi fare l'inversa della tangente: 1  2 2 
  ottenendo 26.56505118° (se la CT è a 10 cifre). Nel caso del vettore (-2,-1) avrei ottenuto lo stesso valore, ma avrei poi dovuto aggiungere 180° (→ figura sopra a destra). ottenendo 26.56505118° (se la CT è a 10 cifre). Nel caso del vettore (-2,-1) avrei ottenuto lo stesso valore, ma avrei poi dovuto aggiungere 180° (→ figura sopra a destra).
Nel caso del  secondo esempio, in cui conosco la prima componente del versore OP, –0.8, posso fare l'inversa del coseno: 0.8 secondo esempio, in cui conosco la prima componente del versore OP, –0.8, posso fare l'inversa del coseno: 0.8 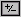
 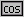 ottenendo 143.1301024°; operando "in radianti" avrei ottenuto 2.498091545. ottenendo 143.1301024°; operando "in radianti" avrei ottenuto 2.498091545.
Cliccando qui accedi a un documento che riporta i valori delle funzioni circolari per alcune direzioni d'uso frequente.
Cliccando qui vedi come tracciare i
grafici in  coordinate polari
usando il computer, con R. coordinate polari
usando il computer, con R.
Esercizi:  su moltiplicaz. vettori per numeri, su moltiplicaz. vettori per numeri,  su direzioni e funz. circolari, su direzioni e funz. circolari,  vari vari
 altri collegamenti [nuova pagina] altri collegamenti [nuova pagina]

Approfondimenti
 Sulla convergenza del Sulla convergenza del  procedimento con cui abbiamo definito le direzioni procedimento con cui abbiamo definito le direzioni
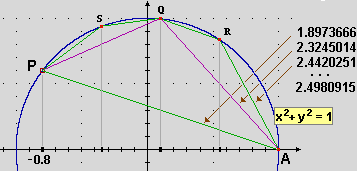
Ecco che cosa si otterrebbe effettuando i calcoli con 16 cifre:
n.tratti L incremento di L
1 1.897366596101028
4 2.442025089203781 0.5446585
16 2.491823296986897 4.979821E-02
64 2.497353652829279 5.530356E-03
256 2.49800211131503 6.484585E-04
1024 2.498080539032038 7.842771E-05
4096 2.498090179859596 9.640828E-06
16384 2.49809137485167 1.194992E-06
65536 2.498091523595386 1.487437E-07
262144 2.498091542149006 1.855362E-08
1048576 2.498091544465845 2.316839E-09
4194304 2.498091544754895 2.890492E-10
|
Da queste uscite possiamo osservare che, man mano che quadruplico il numero dei tratti, i valori aumentano di una quantità man mano circa 10 volte più piccola: passando da 4 a 16 il valore aumenta di circa 5·10–2, da 16 a 64 di circa 6·10–3, da 64 a 256 di circa 6·10–4, ….
All'aumentare del numero dei tratti i valori convergono su un numero particolare, cioè mi consentono di individuarne arrotondamenti man mano a più cifre. Ad esempio il valore finale dell'elenco precedente 2.498091544754895 è stato ottenuto con un incremento di circa 0.0000000003 (3·10–10), il nuovo valore sarà ottenuto con un incremento di circa 0.00000000003 (3·10–11), i successivi incrementi saranno trascurabili: possiamo concludere che il numero su cui i valori tendono a stabilizzarsi è circa 2.49809154478 e è arrotondabile a 2.4980915448.
Effettuando i calcoli con più di 16 cifre e procedendo ulteriormente, si possono trovare arrotondamenti con quante cifre vogliamo della direzione del nostro versore OP.
Se vuoi, qui puoi trovare un programma in JavaScript che
corrisponde al procedimento di calcolo che abbiamo considerato. Qui
ne trovi una più trasparente versione in R.
 Estensione del Estensione del  procedimento con cui abbiamo definito le direzioni al caso di versori con 2ª componente negativa procedimento con cui abbiamo definito le direzioni al caso di versori con 2ª componente negativa
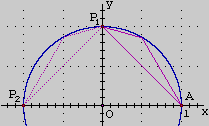
Abbiamo definito la direzione dei versori OP mediante un procedimento riferito al caso in cui yP non è negativo. Se P sta sotto all'asse y il procedimento può essere così modificato:
– l'arco AP è costituito dall'unione dell'arco AB (cioè il semicerchio costituito dai punti del cerchio con ordinata non negativa) e dell'arco BP (i punti del cerchio con ordinata non positiva e ascissa compresa tra –1 e xP); |
– si approssima AB con un tratto rettilineo e si fa lo stesso con BP e si sommano le loro due lunghezze; questa è una approssimazione della lunghezza dell'arco AP (prima figura a destra);
– si approssimano AB e BP con percorsi a 2 tratti rettilinei e si sommano le loro lunghezze; questa è una nuova approssimazione della lunghezza dell'arco AP (seconda figura a destra);
– e così via, prendendo i percorsi a tratti rettilinei nello stesso modo in cui si era fatto nel procedimento originale (i nuovi punti man mano considerati hanno ascissa a metà strada tra la ascissa del punto precedente e quella del punto seguente).
| 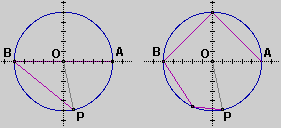 |
|
 I
I  vettori AB ed EF, raffigurati a lato, hanno componenti proporzionali, con
fattore di proporzionalità positivo:
vettori AB ed EF, raffigurati a lato, hanno componenti proporzionali, con
fattore di proporzionalità positivo: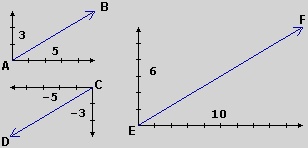





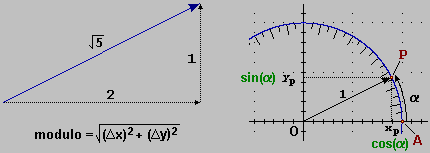

 ,
,  e
e  .
.



 2
2