Distanza
 Nel linguaggio comune con "distanza"
tra due località A e B a seconda dei casi si può
intendere distanza in senso temporale (ma dipende dai mezzi di
trasporto impiegati per raggiungere B da A, dalle caratteristiche del
percorso che si deve seguire, …), o distanza lungo la strada (è
la lunghezza della traiettoria che deve essere percorsa) o distanza
in linea d'aria.
Nel linguaggio comune con "distanza"
tra due località A e B a seconda dei casi si può
intendere distanza in senso temporale (ma dipende dai mezzi di
trasporto impiegati per raggiungere B da A, dalle caratteristiche del
percorso che si deve seguire, …), o distanza lungo la strada (è
la lunghezza della traiettoria che deve essere percorsa) o distanza
in linea d'aria.
In genere, dal contesto del discorso
si comprende a quale distanza ci si riferisce.
In matematica parlando di distanza tra
A e B occorre che sia chiaro qual è lo  spazio S di
cui stiamo considerando i punti A e B e come è stata definita
la distanza, intesa come funzione che a due punti di S associa un
numero reale non negativo.
spazio S di
cui stiamo considerando i punti A e B e come è stata definita
la distanza, intesa come funzione che a due punti di S associa un
numero reale non negativo.
Alla voce "spazio" viene presentata una
possibile definizione di distanza sulla retta dei numeri [ ] e
definizioni di distanze su altri due spazi, quello delle direzioni nel piano [
] e
definizioni di distanze su altri due spazi, quello delle direzioni nel piano [ ] e uno spazio costituito da un insieme finito di punti [
] e uno spazio costituito da un insieme finito di punti [ ].
].
 Per il piano cartesiano [
Per il piano cartesiano [ spazio] le
distanze più usate sono le seguenti:
spazio] le
distanze più usate sono le seguenti:
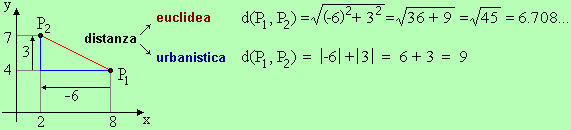
Dati due punti P1 = (x1, y1) e
P2 = (x2, y2), se indichiamo con Δx la variazione orizzontale da
P1 a P2 e con Δy quella verticale, la distanza euclidea è
così definita:
d(P1, P2) = √( (Δx)2 + (Δy)2 ) = √( (x2 – x1)2 + (y2 – y1)2 )
| Questo concetto è un modello matematico della distanza in linea d'aria: |
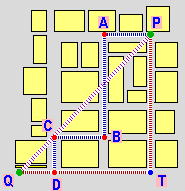
Siano P e Q due punti della cittadina di cui a lato è riprodotta una mappa.
La distanza in linea d'aria tra P e Q può essere calcolata facendo la radice quadrata della somma tra il quadrato del tratto di strada
verticale che va da P a T e il quadrato del tratto orizzontale da T a Q: se misurando trovo che il tratto PT è di 137 m e che il tratto TQ è di 130 m,
posso concludere che in linea d'aria P e Q distano in metri: √(18769+16900) = 188.862… =[arrotondando] 189.
Se invece mi interessa la distanza lungo la strada osservo che le vie sono tutte orizzontali o verticali per cui, sia che faccia il
percorso PTQ (un tratto verticale e uno orizzontale), sia che segua il percorso PABCDQ o altri percorsi in cui si alternano avanzamenti orizzontali e verticali,
la strada da percorrere è comunque la somma dei tratti orizzontali e di quelli verticali: PA+AB+BC+CD+DQ = (PA+BC+DQ)+(AB+CD) = PT+TQ = 267 m. |
 |
 La validità della distanza euclidea come modello matematico
della distanza in linea d'aria può essere "verificata" sperimentalmente, ma solo in modo "approssimato": si può verificare su un foglio di carta
quadrettata o millimetrata (o sulla figura di sopra) che, presi due punti P e Q, misurandone direttamente la distanza con il righello o facendo la radice
quadrata della somma dei quadrati delle loro distanze "in orizzontale" e "in verticale" si ottengono valori non contradditori, cioè compatibili se si
tiene conto delle approssimazioni delle misure [
La validità della distanza euclidea come modello matematico
della distanza in linea d'aria può essere "verificata" sperimentalmente, ma solo in modo "approssimato": si può verificare su un foglio di carta
quadrettata o millimetrata (o sulla figura di sopra) che, presi due punti P e Q, misurandone direttamente la distanza con il righello o facendo la radice
quadrata della somma dei quadrati delle loro distanze "in orizzontale" e "in verticale" si ottengono valori non contradditori, cioè compatibili se si
tiene conto delle approssimazioni delle misure [ calcolo approssimato].
calcolo approssimato].
La scelta di questo modello può essere giustificata facendo vedere, con un ragionamento teorico, che vale la seguente proprietà
(che può essere pensata come c = √(a2+b2) se si tiene conto che i lati dei quadrati
sono le radici quadrate delle loro aree):
due superfici quadrate di lati a e b occupano lo stesso spazio occupato da una superficie quadrata di lato c,
dove c è l'ipotenusa di un triangolo rettangolo di cateti a e b.
[l'ipotenusa è il lato opposto all'angolo retto, i cateti sono gli altri due lati]

Il ragionamento è il seguente (riferito alla figura di sopra): spostando le quattro figure triangolari colorate all'interno della figura
quadrata, la parte rimanente, punteggiata, cambia forma, ma non estensione.
Questa proprietà è nota come teorema di Pitagora (è una denominazione entrata nella
tradizione da molti secoli, anche se l'attribuzione del teorema a Pitagora deriva da alcuni dei molti aneddoti leggendari riferiti a questo filosofo greco,
vissuto nella seconda metà del VI sec. a.C.: la proprietà era nota e usata - sicuramente dai babilonesi e dagli egizi - già un migliaio d'anni prima).
Parlando di "teorema" si intende dire che questa proprietà è dimostrabile. Ma, ad essere rigorosi,
il ragionamento fatto sopra non è una dimostrazione (come  quella che
91 è una soluzione dell'eqazione in x x+36=126), bensì una argomentazione di tipo "fisico" (ad es., che cosa vuol dire "spostare"?).
La proprietà può essere dimostrata "matematicamente" solo se si assume che valga la distanza euclidea o altre proprietà che mi consentano,
ad esempio, di descrivere matematicamente gli spostamenti di una figura, di valutarne l'area, …, che per ora non abbiamo ancora considerato.
E può essere dimostrata solo per un piano matematico astratto in cui valgano queste proprietà: non ha senso dimostrare che un oggetto matematico
sia un "modello esatto" di un fenomeno reale, e in particolare dimostrare che le distanze in linea d'aria si possono determinare mediante la distanza euclidea:
ci dobbiamo accontentare del fatto che le verifiche sperimentali non contraddicano la determinazione delle distanze mediante questa formula.
quella che
91 è una soluzione dell'eqazione in x x+36=126), bensì una argomentazione di tipo "fisico" (ad es., che cosa vuol dire "spostare"?).
La proprietà può essere dimostrata "matematicamente" solo se si assume che valga la distanza euclidea o altre proprietà che mi consentano,
ad esempio, di descrivere matematicamente gli spostamenti di una figura, di valutarne l'area, …, che per ora non abbiamo ancora considerato.
E può essere dimostrata solo per un piano matematico astratto in cui valgano queste proprietà: non ha senso dimostrare che un oggetto matematico
sia un "modello esatto" di un fenomeno reale, e in particolare dimostrare che le distanze in linea d'aria si possono determinare mediante la distanza euclidea:
ci dobbiamo accontentare del fatto che le verifiche sperimentali non contraddicano la determinazione delle distanze mediante questa formula.
Clicca qui per approfondimenti e una rappresentazione animata del teorema di Pitagora.
 La distanza urbanistica è
definita nel modo seguente:
La distanza urbanistica è
definita nel modo seguente:
d(P1, P2) = |Δx| + |Δy| =
|x2 – x1| + |y2 – y1|
Questo concetto è un modello
matematico della distanza tra due incroci in una città in cui
le strade sono tutte disposte orizzontalmente o verticalmente o delle distanze per un robot che possa muoversi solo
orizzontalmente o verticalmente, come illustrato in una  figura precedente.
figura precedente.
|
 Queste due definizioni di distanza
possono essere estese anche allo spazio tridimensionale: Queste due definizioni di distanza
possono essere estese anche allo spazio tridimensionale:
| 
|
|
dati P1 e P2, se P1 = (x1,y1,z1) e P2 = (x1,y2,z2),
abbiamo che tra P1 e P2:
|
|
• la distanza euclidea è | √( (Δx)2 + (Δy)2 + (Δz)2 ) |
|
• quella urbanistica
è | |Δx| + |Δy| + |Δz| |
|
Nel caso raffigurato a fianco, tra (3,2,1) e (5,5,4) la
distanza euclidea è √(22+32+32) = √22 = 4.6904…; quella urbanistica
è 2+3+3 = 8.
|
 La distanza x1, x2:
La distanza x1, x2:
 |x1 – x2| = |Δx| usualmente considerata sulla retta numerica [
|x1 – x2| = |Δx| usualmente considerata sulla retta numerica [ ]
può essere considerata un'evidente estensione della distanza
urbanistica al caso monodimensionale; ma è anche
un'estensione della distanza euclidea, infatti: √((Δx)2)
= |Δx|.
]
può essere considerata un'evidente estensione della distanza
urbanistica al caso monodimensionale; ma è anche
un'estensione della distanza euclidea, infatti: √((Δx)2)
= |Δx|.
 Nota. La distanza d sul piano (sulla
retta, nello spazio tridimensionale, …) può essere
definita anche in modi diversi da quelli che abbiamo considerato.
Devono essere comunque rispettate alcune condizioni, affinché,
in matematica, si possa parlare di distanza:
Nota. La distanza d sul piano (sulla
retta, nello spazio tridimensionale, …) può essere
definita anche in modi diversi da quelli che abbiamo considerato.
Devono essere comunque rispettate alcune condizioni, affinché,
in matematica, si possa parlare di distanza:
• d(P,P) = 0 (un
punto dista 0 da sé stesso) e d(P,Q) 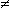 0 se P
0 se P 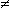 Q
Q
• d(P,Q) = d(Q,P) (la
distanza deve essere simmetrica – cioè commutativa –
: la distanza da P a Q deve essere uguale alla distanza da Q a P,
così che si possa parlare di distanza tra P e Q, senza
specificare qual è il punto di partenza),
• d(P,T) ≤ d(P,Q) + d(Q,T) (intuitivamente: raggiungere direttamente T non può essere più lungo del raggiungerlo passando per un altro punto; è detta diseguaglianza triangolare
in quanto nel caso della distanza euclidea equivale alla proprietà che in un triangolo la
somma delle lunghezze di due lati è maggiore della lunghezza
del terzo).
La distanza in senso temporale,
invece, non soddisfa la condizione di simmetria: se per andare da A a
B devo percorre una strada in salita, la distanza da A a B è
minore della distanza da B a A.
In presenza di "sensi unici" anche la distanza lungo la strada non soddisferebbe la condizione di simmetria.
Esiste, comunque, anche un'area della matematica che si occupa di queste "distanze", anche se le chiama in modo diverso ("quasidistanze").
 Euclide è il nome del matematico greco vissuto intorno al 300 a.C. che nell'opera Gli Elementi (probabilmente con la collaborazione di vari altri matematici) ha dato una organizzazione sistematica a gran parte delle conoscenze geometriche ed aritmetiche fino ad allora conosciute nel mondo mediterraneo, organizzazione che è stata punto di riferimento e prototipo per gli studi matematici per molti secoli.
Euclide è il nome del matematico greco vissuto intorno al 300 a.C. che nell'opera Gli Elementi (probabilmente con la collaborazione di vari altri matematici) ha dato una organizzazione sistematica a gran parte delle conoscenze geometriche ed aritmetiche fino ad allora conosciute nel mondo mediterraneo, organizzazione che è stata punto di riferimento e prototipo per gli studi matematici per molti secoli.
In essa, in particolare, sono illustrate e dimostrate molte proprietà della geometria piana; esse sono svolte in modo molto dettagliato, mescolando ragionamenti e definizioni rigorose ad argomentazioni e descrizioni basate sull'intuizione fisica, simili a quella sopra riportata per giustificare il "teorema di Pitagora".
La definizione e la riflessione sugli oggetti matematici svincolate da giustificazioni basate sulla evidenza "fisica" è diventata una caratteristica della matematica solo nel XIX secolo, e in modo graduale.
Prima i matematici, in realtà, non erano tanto dei matematici come li intendiamo noi, ma degli studiosi più generali che sviluppavano riflessioni filosofiche (esiste l'infinito? quali sono le forme di ragionamento corrette? …) e/o fisiche (che cosa è lo spazio? come misurare un volume? come descrivere il movimento di un corpo? …) e/o artistiche (come disegnare una scena in modo che assomigli a come la vedrebbe effettivamente il nostro occhio) e/o ingegneristiche (come inclinare il cannone in modo da ottenere una data gittata? …).
Gli stessi personaggi che si trovano in un libro di storia della matematica si possono trovare in un libro di storia della filosofia o di storia della fisica o di storia dell'arte o ….
La trattazione della geometria sviluppata negli Oggetti Matematici cerca di rispecchiare il modo in cui si fa, e si usa, la matematica negli ultimi secoli.
È in questo periodo che è stato messo a punto il concetto generale di distanza e che è stata chiamata geometria euclidea quella basata sulla distanza euclidea.
Il termine distanza euclidea è stato adottato in quanto la distanza con esso indicata corrisponde a quella intutivamente utilizzata da Euclide, e che per lui era l'unico concetto di distanza ammissibile.
Vedrai in studi più avanzati che, in effetti, anche in fisica, per studiare fenomeni ad esempio di tipo astronomico, la distanza euclidea non è un  modello matematico adeguato. Qualche riflessione ulteriore su questi problemi la trovi più avanti, alla voce
modello matematico adeguato. Qualche riflessione ulteriore su questi problemi la trovi più avanti, alla voce  triangoli.
triangoli.
Esercizi:  ,
,  ,
, 
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Nel linguaggio comune con "distanza"
tra due località A e B a seconda dei casi si può
intendere distanza in senso temporale (ma dipende dai mezzi di
trasporto impiegati per raggiungere B da A, dalle caratteristiche del
percorso che si deve seguire, …), o distanza lungo la strada (è
la lunghezza della traiettoria che deve essere percorsa) o distanza
in linea d'aria.
Nel linguaggio comune con "distanza"
tra due località A e B a seconda dei casi si può
intendere distanza in senso temporale (ma dipende dai mezzi di
trasporto impiegati per raggiungere B da A, dalle caratteristiche del
percorso che si deve seguire, …), o distanza lungo la strada (è
la lunghezza della traiettoria che deve essere percorsa) o distanza
in linea d'aria.

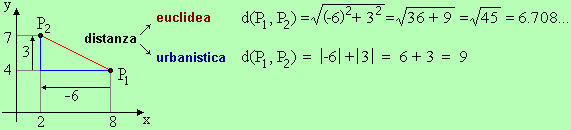



 |x1 – x2| = |Δx| usualmente considerata sulla retta numerica [
|x1 – x2| = |Δx| usualmente considerata sulla retta numerica [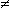 0 se P
0 se P 
