Equazioni differenziali - 1

  Esempi

Suppongo di sapere che un corpo A si muove alla velocità costante di 8 m/s e che un corpo B si muove alla velocità crescente di (3 t + 1.5) m/s, dove t è il tempo espresso in secondi dall'istante t = 0 in cui l'oggetto è partito.

    Se indico con x_A e con x_B la strada in metri percorsa dai due oggetti dopo t secondi, posso scrivere:

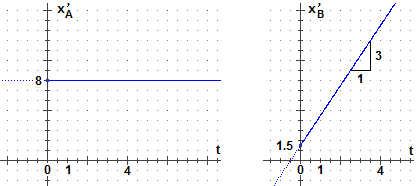d xA	= 8
——
d t
d xB	= 3 t + 1.5
——
d t

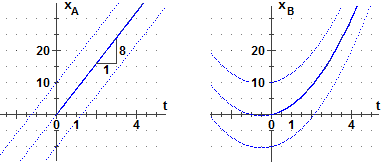Posso ricavare:   xA = 8 t ma anche:   xA = 8 t + 10,  xA = 8 t − 10, … e:   xB = 1.5 t2 + 1.5 t,   xB = 1.5 t2 + 1.5 t + 10,  xB = 1.5 t2 + 1.5 t − 10, …

Abbiamo tracciato anche i tratti corrispondenti a  t < 0, in quanto, in entrambi i casi, avremmo potuto considerare un istante precedente a  t = 0.  Le "soluzioni", ossia le equazioni che esprimono x_A e x_B in funzione di t, sono in entrambi i casi infinite:  solo se fisso la posizione in un istante fissato, ad es. per t = 0, posso individuare una particolare soluzione.

  Se invece so che la derivata prima di g è x → |x|  ( g '(x) = |x|; qui, a differenza che nell'esempio precedente, ho indicato con x la variabile indipendente), che cosa posso dire di g ?

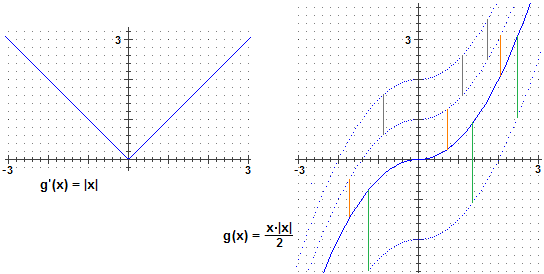
Per x ≥ 0  g '(x) = x:  quindi  g(x) = x²/2.   Per x ≤ 0  g '(x) = −x:  quindi  g(x) = −x²/2.  Posso riassumere tutto con:  g(x) = x · |x| / 2.

    Ma il "quindi" non è corretto:  anche  g(x) = x · |x| / 2 + 1,  g(x) = x · |x| / 2 + 2,  g(x) = x · |x| / 2 − 2, … soddisfano l'equazione di partenza,  g '(x) = |x|.

    Sopra, a destra, sono state tracciati i grafici di alcune funzioni che verificano l'equazione di partenza, ed è evidenziato come esse differiscano per una costante:  abbiamo messo in luce la cosa in quanto essa non è evidente come nei casi considerati nel punto precedente, anche se, inevitabilmente, deve accadere.

  Equazioni (e modelli) differenziali

Gli esempi visti nei due paragrafi precedenti possono essere riassunti nel modo seguente, in cui abbiamo indicato con f la funzione incognita, con x la variabile indipendente, e con c una qualunque costante:
      f '(x) = 8,  f(x) = 8x + c       f '(x) = 3x + 1.5,  f(x) = 1.5x² + 1.5x + c       f '(x) = |x|,  f(x) = x·|x|/2 + c

In tutti e tre i casi abbiamo che l'equazione considerata  f '(x) = ...  ha infinite soluzioni:
      f(x) = 8x + 10,  f(x) = 8x,  f(x) = 8x − 10,  ... sono soluzioni di   f '(x) = 8,
      f(x) = 1.5x² + 1.5x + 10,  f(x) = 1.5x² + 1.5x,  f(x) = 1.5x² + 1.5x − 10,  ... sono soluzioni di   f '(x) = 3x + 1.5,
      f(x) = x · |x| / 2 + 1,  f(x) = x · |x| / 2 ,  f(x) = x · |x| / 2 − 2  ... sono soluzioni di   f '(x) = |x|.

L'equazione  f '(x) = ...  viene chiamata equazione differenziale nell'incognita f(x). Essa, come abbiamo visto, ha infinite soluzioni  f(x) = ... + c, una per ogni valore di c, che corrispondono a grafici paralleli, ottenibili uno dall'altro mediante una traslazione verticale.

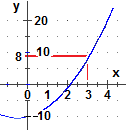
Se fissiamo un punto (x0, y0) per cui deve passare il grafico otteniamo una sola funzione (a patto, naturalmente, che x0 stia nel dominio di f ' e che questo sia un intervallo).  In questo caso si usa dire che la funzione trovata è una soluzione del  modello differenziale  "f '(x) = ...  e  f(x0) = y0".  Ad esempio di fronte a  f '(x) = 3x + 1.5  e alla richiesta che f(3) = 8 ottengo: f(x) = 1.5x2 + 1.5x + c  AND  f(3) = 8; 8 = 1.5·9 + 1.5·3 + c;       c = 8 − 18 = −10; f(x) = 1.5x2 + 1.5x − 10   (vedi figura a fianco).

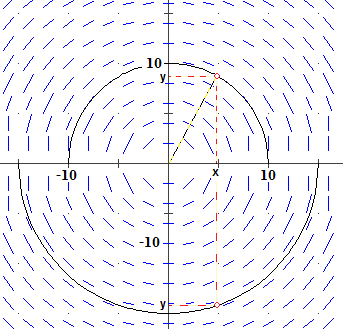
Se l'equazione, però, contiene la funzione incognita anche senza il simbolo di derivata, come nell'esempio seguente:         f '(x) = − x / f(x) in genere scritto così (indicando la funzione incognita con y):         y'(x) = − x / y(x) l'equazione non ha necessariamente soluzioni corrispondenti tutte a grafici paralleli: come si vede a destra, in cui sono tracciati tanti trattini con pendenza -x/y, nel caso considerato la pendenza y' a una curva soluzione deve essere perpendicolare al segmento che congiunge l'origine con (x, y)  (vedi figure 2), e quindi le soluzioni dell'equazione hanno tutte come grafico dei mezzi cerchi con centro nell'origine, rivolti verso il basso (nel caso in cui la curva debba passare per (x0,y0) con y0 > 0) o rivolti verso l'alto (nel caso in cui la curva debba passare per (x0,y0) con y0 < 0):  nella figura a lato, per lo stesso x0, sono state tracciate due soluzioni una avente ordinata y0 positiva, una avente ordinata y0 negativa. Qui come ottenere la rappresentazione grafica con R.

Alla voce  derivata e differenziale abbiamo visto vari altri esempi di funzioni dallo studio della cui derivata (dove cresce o decresce, dove si annulla, ...) possiamo dedurre informazioni relative alla funzione di partenza. In ogni caso, noto il valore di f ' e fissata una coppia (x0, y0), possiamo ricavare un'unica funzione f tale che f ' = ..., che è definita in un intervallo contenente x0 e tale che f(x0) = y0.     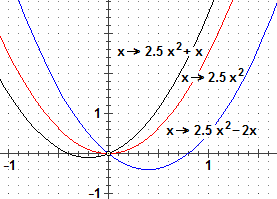Se, invece, avessimo un problema del tipo  f "(x) = ...  dove f " indica la derivata della derivata di f, fissata (x0, y0) potremmo avere più soluzioni f tali che f(x0) = y0.     Se ad esempio avessimo  f "(x) = 5, avremmo che  f '(x) = 5x + c'  e, quindi,  f(x) = 2.5x2 + c'x + c"  verifica l'equazione iniziale, qualunque siano i valori di c' e di c".  A destra sono raffigurate tre tra le infinite funzioni f che risolvono f "(x) = 5 e sono tali che f(0) = 0.     Si vedrà in una successiva voce che potrà ottenersi un'unica soluzione che soddisfa l'equazione  f "(x) = ...  se si imporrà un'ulteriore condizione:  qual è il valore che assume f '(x0). Qui limitiamoci a due esempi.

(1)  Consideriamo il caso in cui  s"(t) = 5  sia l'accelerazione costante in m/s² di un'automobile che all'istante t = 0 (t espresso in secondi) sia nella posizione s = 0 (s espressa in metri).  Sono infinite le curve che potrebbero descrivere il moto della nostra automobile:  s(t) = 2.5 t² + t, s(t) = 2.5 t², s(t) = 2.5 t² − 2t, …  hanno  s'(t) = 5 t + 1, s'(t) = 5 t, s'(t) = 5 t − 2, …  e, tutte, s"(t) = 5, oltre a  s(0) = 0.  Se imponiamo, per esempio, che s'(0) = 3, ricaviamo s'(0) = 5·0 + 3 = 3, da cui  s(t) = 2.5 t² + 3t.  Se imponiamo che  s'(0) = 0  ricaviamo  s(t) = 2.5 t².

(2)  Consideriamo, poi, il caso di una molla sospesa per una estremità a cui viene appeso un oggetto. Se l'oggetto non è troppo pesante, la molla non perde elasticità e, se il peso viene tolto, ritorna alla posizione iniziale. In queste condizioni abbiamo che l'allungamento della molla è proporzionale alla forza peso che le viene applicata. Supponiamo di essere di fronte ad una molla tale che F = −k·x dove F è la forza peso (espressa in newton: 1 N ≈ 1/9.81 kg_peso) esercitata dalla massa appesa, x è l'allungamento (espresso in metri) e k è una grandezza costante (espressa in N/m, se le altre grandezze sono espresse in newton e metri).
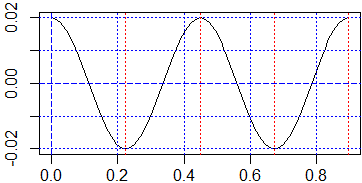
Se sposto la massa di 0.02 m e la rilascio, la massa comincia ad oscillare. Quali sono il periodo e l'ampiezza della oscillazione, e, più in generale, come varia x al trascorrere del tempo t (in secondi)? Nelle unità di misure fissate, posso esprimere F come m·x"(t) (l'accelerazione è pari alla derivata seconda di x rispetto a t), per cui il problema si traduce nella equazione differenziale  m·x"(t) = −k·x(t),  ovvero  x"(t) = −k/m·x(t).  Conosciamo la posizione iniziale, x(0) = 0.02, e la velocità iniziale, x'(0) = 0 (la molla inizialmente è ferma).
Se fosse x(t) = sin(t) avremmo x'(t) = cos(t) e x"(t) = −sin(t) = −x(t). Questo ci dà un'idea di come è la soluzione.
Con semplici manipolazioni si trova che x(t) = 0.02·sin(√(k/m)·t+π/2).
Il periodo dell'oscillazione è t tale che √(k/m)·t = 2π, ossia 2π√(m/k).
Ad esempio se m = 0.2 kg e la molla, rispetto alla posizione di riposo, si allunga di 5 cm, da F = −k·x abbiamo 0.2·g kg = k·0.05 m, da cui k = 39.2 N/m. Il periodo è dunque:  2π√(0.02/39.2) s = 0.448799 s = 0.449 s (arrotondando).

(come realizzare il grafico a fianco con R,  e come risolvere l'equazione con WolframAlpha)

 altri collegamenti     [nuova pagina]