Figure 1
 Con figura intendiamo un insieme di punti in un dato
Con figura intendiamo un insieme di punti in un dato  spazio. Ad esempio nello spazio "retta numerica" [
spazio. Ad esempio nello spazio "retta numerica" [ ], presi due punti-numeri a e b, possiamo considerare il segmento costituito dai punti x tali che a ≤ x ≤ b (si veda la figura sotto a sinistra).
], presi due punti-numeri a e b, possiamo considerare il segmento costituito dai punti x tali che a ≤ x ≤ b (si veda la figura sotto a sinistra).
Possiamo rendere compatta la descrizione di molte figure abbreviando "l'insieme degli α tali che sia vera la
condizione Γ" con:
{ α t.c. Γ } o { α : Γ } o { α / Γ } o { α | Γ }
Ecco tre semplici esempi di figure riferiti agli spazi numerici a 1, 2 e 3
dimensioni [ ]:
]:
| {x : a ≤ x ≤ b} |
{(x,y) : a ≤ x ≤ b AND c ≤ y ≤ d} |
 |
 |
 |
{(x,y,z) : a ≤ x ≤ b AND c ≤ y ≤ d AND e ≤ z ≤ f} |
Qualche altro esempio riferito al caso bidimensionale (qui d è la distanza euclidea):
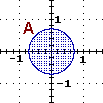 |  |  |  | 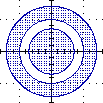 |
{(x,y) : x2+y2 ≤ 1/2}
ossia:
{P : d(P,O) ≤ √(1/2)} |
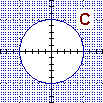
{(x,y) : x2+y2 ≤ 2}
ossia:
{P : d(P,O) ≤ √2} |
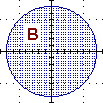
{(x,y) : 1 ≤ x2+y2}
ossia:
{P : 1 ≤ d(P,O)} |
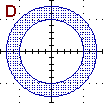
{(x,y) : 1 ≤ x2+y2 ≤ 2}
intersezione
tra B e C |
{(x,y) : 1 ≤ x2+y2 ≤ 2
OR x2+y2 ≤ 1/2}
unione di A e D |
Nota. A volte si sottointende {(…) : …} e si scrive semplicemente la condizione. Ad esempio per indicare la retta del piano costituita dai punti di ascissa 1 invece di {(x,y) : x=1} si scrive "la retta x=1" o "la retta di equazione x=1".
 Soffermiamoci sul caso bidimensionale, cioè sul piano cartesiano [
Soffermiamoci sul caso bidimensionale, cioè sul piano cartesiano [ ].
].
La figura  al centro nell'illustrazione iniziale è un
rettangolo; facendo variare a, b, c e d otteniamo tutti i rettangoli con lati paralleli agli assi.
al centro nell'illustrazione iniziale è un
rettangolo; facendo variare a, b, c e d otteniamo tutti i rettangoli con lati paralleli agli assi.
Per dare una
definizione puramente matematica che comprenda anche i rettangoli
con lati non paralleli agli assi, che si possono ottenere da
figure come questa mediante una rotazione, occorre disporre prima di una definizione
matematica del concetto di rotazione [ trasformazioni geometriche] o del concetto di perpendicolarità (derivabile da quello di rotazione:
trasformazioni geometriche] o del concetto di perpendicolarità (derivabile da quello di rotazione:  figure2).
figure2).
|
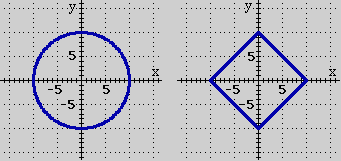
 A fianco sono rappresentate le figure costituite dai punti che
distano 10 dall'origine rispettivamente secondo la A fianco sono rappresentate le figure costituite dai punti che
distano 10 dall'origine rispettivamente secondo la  distanza
euclidea e secondo la distanza urbanistica, cioè: distanza
euclidea e secondo la distanza urbanistica, cioè:
{ (x,y) : x2 + y2 = 100 } e
{ (x,y) : |x| + |y| = 10 }
Nota. √(x2+y2) = 10 equivale a x2+y2 = 100 poiché 0 ≤ x2+y2
|
|
Nell'ambito della geometria piana euclidea, cioè dello studio delle figure del piano cartesiano dotato della distanza euclidea, la figura a sinistra è il cerchio di centro (0,0) e
raggio 10.
La figura a destra è un quadrato. Per dare una definizione generale di quadrato occorre far riferimento ad ulteriori concetti (vedi quanto osservato sopra a proposito dei rettangoli). Qui ci limitiamo a osservare che le distanze da un
vertice al successivo, ad esempio dal punto (0,10) al punto (10,0),
sono tutte uguali a √(102+102) = √200 e che le diagonali, cioè le distanze da
un vertice al vertice opposto, sono tutte uguali a 20.
Nota. La figura soprastante a destra (nella geometria euclidea)
è un quadrato. È anche un rombo,
come ogni quadrato, ma, appunto, non è solo un rombo: un quadrato non ha necessariamente i lati orizzonali
e verticali.
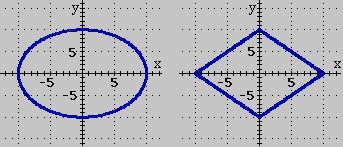
 Se non avessimo scelto un sistema monometrico [
Se non avessimo scelto un sistema monometrico [ pendenza] avremmo
potuto ottenere le rappresentazioni seguenti.
pendenza] avremmo
potuto ottenere le rappresentazioni seguenti.
|
L'aspetto non è più quello di un "cerchio"
o di un "quadrato": se misuriamo "fisicamente" le
distanze con un righello, i punti della figura a sinistra non hanno
la stessa distanza dal punto (0,0) e le due diagonali della seconda
figura non hanno la stessa lunghezza.
|
|
Ma dal punto di vista "matematico", riferendosi al piano
cartesiano e alla distanza euclidea, siamo solo di fronte a una
diversa rappresentazione concreta delle stesse figure. Quindi, ad
esempio, la figura disegnata a sinistra è un "cerchio".
Abbiamo già fatto una analoga distinzione tra la  pendenza "stradale" e quella "dei grafici".
pendenza "stradale" e quella "dei grafici".
 Nota. Per rappresentare graficamente figure descritte mediante
equazioni, come le due figure precedenti, posso ricorrere a programmi in grado di rappresentare equazioni del tipo
E(x,y)=0, come, appunto, x2+y2–100=0 e
|x|+|y|–10=0 (vedi
Nota. Per rappresentare graficamente figure descritte mediante
equazioni, come le due figure precedenti, posso ricorrere a programmi in grado di rappresentare equazioni del tipo
E(x,y)=0, come, appunto, x2+y2–100=0 e
|x|+|y|–10=0 (vedi  qui per farlo con R).
qui per farlo con R).
Posso provare a realizzare tali figure anche mediante il tracciamento di grafici di funzioni. Devo, però, trasformare l'equazione in una equazione o in
più equazioni del tipo y=…, cioè risolvere
l'equazione rispetto a y.
Nei nostri casi abbiamo che:
| x2 + y2 – 100 = 0 |
equivale a |
y = √(100 – x2)
OR
y = –√(100 – x2) |
|
|
|x| + |y| – 10 = 0 |
equivale a |
(y = 10 – |x| AND –10 ≤ x ≤ 10) OR
(y = – (10 – |x|) AND –10 ≤ x ≤ 10) |
 |
Esercizi:
 ,
,

 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Con figura intendiamo un insieme di punti in un dato
Con figura intendiamo un insieme di punti in un dato  spazio. Ad esempio nello spazio "retta numerica" [
spazio. Ad esempio nello spazio "retta numerica" [ ], presi due punti-numeri a e b, possiamo considerare il segmento costituito dai punti x tali che a ≤ x ≤ b (si veda la figura sotto a sinistra).
], presi due punti-numeri a e b, possiamo considerare il segmento costituito dai punti x tali che a ≤ x ≤ b (si veda la figura sotto a sinistra).







 x/2 con la figura che si ottiene da essa mediante la traslazione
con passi Δx = 0, Δy = –1.5,
x/2 con la figura che si ottiene da essa mediante la traslazione
con passi Δx = 0, Δy = –1.5,




