Figure (2)
Consideriamo alcune  figure della
figure della  geometria piana euclidea.
geometria piana euclidea.
 La semiretta di
origine A e direzione α è l'insieme
dei punti che possono essere ottenuti da A con traslazioni di
La semiretta di
origine A e direzione α è l'insieme
dei punti che possono essere ottenuti da A con traslazioni di
 direzione α. Intuitivamente, è la figura generata da un punto che parte da una posizione fissata e prosegue (oltre ogni limite) in una direzione fissata.
direzione α. Intuitivamente, è la figura generata da un punto che parte da una posizione fissata e prosegue (oltre ogni limite) in una direzione fissata.
Potremmo anche dire, equivalentemente, che è una semiretta ogni figura "uguale" alla parte "non negativa" dell'asse x ( {(x,0) : 0 ≤ x} ), ossia ottenibile da essa con una rotazione attorno a (0,0) e una traslazione; la sua orgine è il trasformato di (0,0); la sua direzione è l'ampiezza della rotazione con cui è stata ottenuta.
Se B è un altro
punto della semiretta, possiamo chiamarla anche semiretta AB
(la direzione è quella del vettore AB). Il segmento
AB è l'insieme dei punti ottenibili da A con traslazioni di modulo
minore o uguale a d(A,B); intuitivamente, è la figura generata da un punto che parte da una posizione
fissata e prosegue in una direzione fissata fino a raggiungere una certa distanza dalla posizione iniziale.
Questa distanza viene chiamata lunghezza del segmento, e a volte indicata con 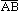 (solo se A e B coincidono, ossia se il segmento si riduce ad un punto, la lunghezza di AB è nulla e, ovviamente,
la direzione da A a B non è fissata).
Il suo punto medio, generalizzando quanto visto per gli
(solo se A e B coincidono, ossia se il segmento si riduce ad un punto, la lunghezza di AB è nulla e, ovviamente,
la direzione da A a B non è fissata).
Il suo punto medio, generalizzando quanto visto per gli  intervalli,
è il punto di esso equidistante dagli estremi, ossia ((xA+xB)/2, (yA+yB)/2).
intervalli,
è il punto di esso equidistante dagli estremi, ossia ((xA+xB)/2, (yA+yB)/2).
Potremmo anche dire che è un segmento ogni figura "uguale" a un intervallo limitato dell'asse x, ossia ottenibile ruotando e traslando intervalli limitati dell'asse x.

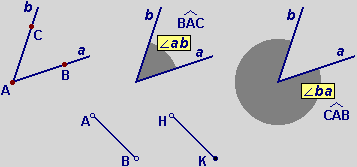
Dati
una semiretta a e un numero φ, con 0° ≤ φ ≤ 360°,
l'unione delle semirette ottenute da a con rotazioni
antiorarie attorno all'origine di a di ampiezza minore o
uguale a φ viene chiamata angolo ab (e indicata ∠ab) dove b è la semiretta ottenuta con la rotazione
ampia φ (al posto del simbolo "∠" si usa anche il simbolo "^": vedi la figura precedente). L'origine di queste semirette viene chiamata vertice dell'angolo. Intuitivamente un angolo è una figura generata dalla rotazione di una semiretta attorno alla sua origine.
L = d(A,B) è la lunghezza
del segmento AB, A e B ne sono gli estremi.
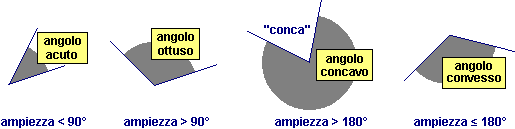
φ è l'ampiezza
dell'angolo ab, a e b ne sono i lati.
Se φ = 0° (angolo nullo, ridotto a una semiretta) o φ = 360° (angolo giro, pari a tutto il piano) i lati dell'angolo coincidono; quando i lati coincidono occorre specificare quale, tra 0° e 360°, si considera come ampiezza.
Nota. I movimenti piani conservano, oltre alle distanze, anche le ampiezze angolari. Infatti le traslazioni non modificano le direzioni delle semirette, mentre le rotazioni le modificano tutte della stessa quantità. Lo stesso accade per le simmetrie (che, però, invertono l'ordine con cui devono essere considerati i lati).
 I seguenti disegni
richiamano altre definizioni (alcune sono precisate più avanti):
I seguenti disegni
richiamano altre definizioni (alcune sono precisate più avanti):
 Una retta è
l'unione di due Una retta è
l'unione di due  semirette di origine comune e direzioni opposte. Tra
le due direzioni, quella che cade in [0°,180°) viene
chiamata inclinazione della retta. semirette di origine comune e direzioni opposte. Tra
le due direzioni, quella che cade in [0°,180°) viene
chiamata inclinazione della retta.
Potremmo anche dire che è una retta ogni figura "uguale" all'asse x, ossia ottenibile da esso con una rotazione e una traslazione. | 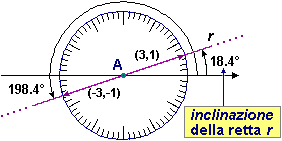 |
| | r : punti raggiungibili da A procedendo nella direzione del vettore (3,1) o del vettore opposto. |
 Rette con la stessa
inclinazione si chiamano parallele. Rette con
inclinazioni che differiscono di 90° si chiamano perpendicolari. Il fatto che due rette r e s siano parallele e quello che siano perpendicolari sono spesso indicati con, rispettivamente, r // s e r ⊥ s.
Rette con la stessa
inclinazione si chiamano parallele. Rette con
inclinazioni che differiscono di 90° si chiamano perpendicolari. Il fatto che due rette r e s siano parallele e quello che siano perpendicolari sono spesso indicati con, rispettivamente, r // s e r ⊥ s.
Ogni retta con inclinazione
diversa da 90° è descrivibile come il grafico di una
funzione del tipo x  ax+b (funzione lineare), il cui output
ax+b (funzione lineare), il cui output  varia proporzionalmente alla variazione dell'input: si veda la figura sotto a sinistra.
varia proporzionalmente alla variazione dell'input: si veda la figura sotto a sinistra.
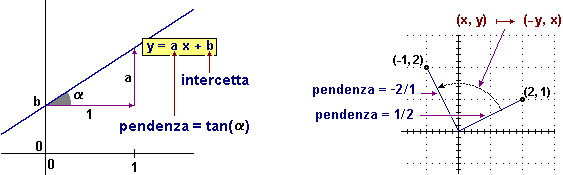
Due funzioni lineari con
pendenze p1 e p2 hanno grafici paralleli quando
p1 = p2. Hanno grafici perpendicolari quando
p1 = –1/p2: infatti (vedi figura sopra a destra) la funzione che trasforma un punto nel suo ruotato di 90° attorno a (0,0) scambia i valori assoluti di x e y e cambia il segno della prima coordinata.
Due insiemi di oggetti matematici vengono detti incidenti
se hanno "almeno" un oggetto in comune. In particolare,
due segmenti, semirette o due rette, o due figure in generale, sono incidenti se hanno almeno un punto in comune.
Nel caso di due semirette S e T col vertice in comune, si chiama angolo di incidenza
l'angolo ∠ST; se S e T coincidono, l'angolo è nullo (in alcuni manuali, erroneamente,
si mette la condizione che il punto sia "esattemente" uno, perdendo il caso degli angoli nulli; controllate la
definzione che usa il libro, per interpretare correttamente ciò che in esso si intende dire). Il termine
deriva dal verbo latino incidere, che significava cadere; ne fece uno dei primi usi
Galileo chiamando incidente un raggio di luce che incontra una superficie e punto di incidenza
il punto di incontro.
 Dati tre punti A, B e C non allineati (cioè tali che non esista una retta a cui appartengano tutti e tre), il triangolo
ABC è (vedi figura a lato) l'unione dei segmenti AP al variare di P su BC. Ovvero (vedi figura sottostante) è l'intersezione dei tre semipiani (1), (2) e (3) delimitati rispettivamente dalle rette AB, BC e CA e contenenti rispettivamente C, A e B. I tre angoli di vertici A, B e C generati dalle rotazioni di AB su AC (vedi figura a lato), di BC su BA e di CA su CB sono gli angoli del triangolo. Dati tre punti A, B e C non allineati (cioè tali che non esista una retta a cui appartengano tutti e tre), il triangolo
ABC è (vedi figura a lato) l'unione dei segmenti AP al variare di P su BC. Ovvero (vedi figura sottostante) è l'intersezione dei tre semipiani (1), (2) e (3) delimitati rispettivamente dalle rette AB, BC e CA e contenenti rispettivamente C, A e B. I tre angoli di vertici A, B e C generati dalle rotazioni di AB su AC (vedi figura a lato), di BC su BA e di CA su CB sono gli angoli del triangolo. | 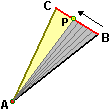 |
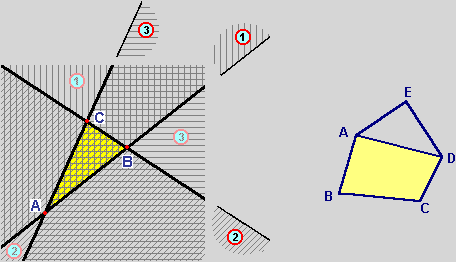
Gli
altri poligoni ( "figure dai molti angoli", dalle parole greche polís, molto, e gonia, angolo) sono ottenibili a partire da un
triangolo mediante successive, opportune, unioni di nuovi triangoli:
dato un n-agono (ABCD nel disegno soprastante) si ottiene un n+1-agono se si unisce un triangolo che abbia
in comune con esso solo un lato (AD) e abbia l'altro vertice (E) non allineato con i lati "vicini" (AB e DC); i lati del nuovo poligono sono n+1: i lati del vecchio poligono e quelli del triangolo escluso il lato comune; gli n+1 angoli sono gli n-2 angoli del vecchio poligono (vertici B e C) e l'angolo del triangolo (E) non delimitati dal lato comune, e i due nuovi angoli ottenuti unendo i rimanenti angoli del vecchio poligono e del triangolo (vertici A e D).
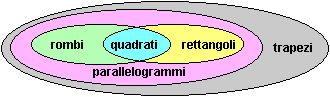
Richiamiamo che cosa sono alcuni particolari tipi di poligono. I rettangoli possono essere definiti, oltre che nel modo accennato alla voce  figure (1) (come frutto di rotazioni di rettangoli a lati paralleli agli assi o come quadrangoli con gli angoli retti), anche come generati da un segmento che viene traslato perpendicolarmente a sé stesso: l'unione dei segmenti ottenibili da un segmento dato l traslandolo con vettori di modulo minore o uguale ad un numero fissato h e aventi come direzione una delle due direzioni perpendicolari al segmento (l e h vengono a volte chiamati "base" e "altezza" del rettangolo). I parallelogrammi, oltre che come quadrangoli con i lati a due a due paralleli, possono essere descritti come le figure generate da un segmento che viene traslato con vettori di direzione fissata (non parallela al segmento) e modulo minore o uguale ad un numero fissato. I rombi sono quadrangoli con i lati uguali. I quadrati, oltre che nel modo accennato alla voce
figure (1) (come frutto di rotazioni di rettangoli a lati paralleli agli assi o come quadrangoli con gli angoli retti), anche come generati da un segmento che viene traslato perpendicolarmente a sé stesso: l'unione dei segmenti ottenibili da un segmento dato l traslandolo con vettori di modulo minore o uguale ad un numero fissato h e aventi come direzione una delle due direzioni perpendicolari al segmento (l e h vengono a volte chiamati "base" e "altezza" del rettangolo). I parallelogrammi, oltre che come quadrangoli con i lati a due a due paralleli, possono essere descritti come le figure generate da un segmento che viene traslato con vettori di direzione fissata (non parallela al segmento) e modulo minore o uguale ad un numero fissato. I rombi sono quadrangoli con i lati uguali. I quadrati, oltre che nel modo accennato alla voce  figure (1) (ottenibili traslando e ruotando figure di equazione |x| + |y| = k, con k numero positivo), possono essere definiti come figure che sono sia rombi che rettangoli.
figure (1) (ottenibili traslando e ruotando figure di equazione |x| + |y| = k, con k numero positivo), possono essere definiti come figure che sono sia rombi che rettangoli.
I trapezi sono quadrangoli con una coppia di lati paralleli. I triangoli [e i trapezi] sono detti triangoli [trapezi] rettangoli se hanno un angolo retto e isosceli ("con i gambi uguali", dalle parole greche ísos, uguale, e skélos, gambo) se hanno due lati [non consecutivi] uguali.
In tutti e questi i tre casi ad essere rigorosi avremmo dovuto aggiungere "almeno" davanti a, rispettivamente, "una coppia di lati paralleli", "un angolo retto" e "due lati uguali"
per esplicitare il fatto ve ne possono essere altri.
Infatti tra i triangoli isosceli vengono considerati in particolare quelli equilateri (che hanno 3 lati uguali),
tra i trapezi vengono considerati anche i parallelogrammi (che hanno due coppie di lati paralleli)
e tra quelli rettangoli vengono considerati anche i rettangoli (che hanno 4 angoli retti - e comunque ogni trapezio rettangolo ha almeno 2 angoli retti).
In genere, in una definizione, quando si vuole precisare che vi sono N elementi con una certa proprietà e non ve ne sono altri,
si dice "esattamente N". Vengono detti triangoli scaleni quelli che hanno i lati diversi
l'uno dall'altro.
 Note. Note.
• L'angolo ∠ab, se
a è la semiretta AB e b è la semiretta
AC, viene indicato anche ∠BAC (o con "^" sopra a BAC).
• Quando il contesto non è
ambiguo, si possono usare le notazioni ∠BAC e ∠CAB (∠ab e ∠ba)
per indicare indifferentemente l'angolo generato dalla rotazione
(antioraria) della semiretta AB verso la semiretta AC o l'angolo
generato dalla rotazione della semiretta AC verso la semiretta AB.
• A volte, in analogia con
quanto accade per gli  intervalli, si possono
considerare segmenti, semirette, semipiani, poligoni, …privati di
estremi, origine, lati, …. intervalli, si possono
considerare segmenti, semirette, semipiani, poligoni, …privati di
estremi, origine, lati, ….
|  |
• Esistono anche diverse
interpretazioni dei termini poligono e cerchio,
a seconda che si considerino solo il contorno o anche i punti
interni. Anche qui a volte le due parole sono usate in entrambi i modi:
in genere dal contesto si capisce quando ci si riferisce solo al contorno o anche ai punti interni.
Osserviamo che c'è chi, considerando parte del "cerchio" anche i punti interni, usa la
parola circonferenza per indicare ciò che qui abbiamo definito come cerchio
(noi la useremo per indicare la lunghezza del cerchio,
come del resto si fa nel linguaggio comune e nel linguaggio scientifico internazionale); a volte, per indicare il contorno del cerchio si usa anche la parola circolo. |
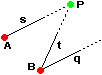 |
• Nel linguaggio comune si dice che (vedi fig. a sinistra) muovendosi da A e B verso il punto P si va nella stessa direzione: si è diretti verso la stessa meta. In matematica invece le due traiettorie (ossia le semirette s e t) vengono considerate di direzione diversa, mentre si considerano ugualmente dirette solo traiettorie come s e q. |
• Mentre in matematica con angolo si intende una parte illimitata di piano, nel linguaggio comune con questa parola si indica una zona dell'angolo vicina al vertice: quando si dice «la sedia che sta in quell'angolo» ci si riferisce a quella che è vicina al vertice di esso (ogni altra sedia che sta nella stanza - se questa non ha una forma "strana" - sta in quell'angolo). Si noti che la parola stessa lato in matematica è usata con un significato quando è riferita a un poligono (indica un segmento) e con un altro quando è riferita a un angolo (indica una semiretta). |
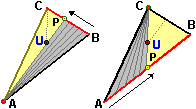 |
• Abbiamo definito il triangolo come la parte di piano “spazzata" da un segmento con un estremo fissato su un vertice e l'altro che si sposta sul segmento che ha per estremi gli altri due vertici. Se avessimo scelto in maniera diversa l'estremo fissato (vedi immagine a lato) avremmo ottenuto la stessa figura? Come si vede nell'immagine, ogni punto U della figura generata nel modo illustrato a sinistra (che sta sulla semiretta AU) fa parte anche della figura generata nel modo illustrato a destra (sta anche sulla semiretta CU). Analogamente, facendo riferimento alla definizione di poligono, si può osservare che lo stesso poligono può essere costruito unendo triangoli diversi. |
 Il cerchio di
centro C e raggio r è l'insieme dei punti che distano r
da C:
Il cerchio di
centro C e raggio r è l'insieme dei punti che distano r
da C:
{ P : d(P,C) = r } =
{ (x,y) : (x – xC)2 + (y – yC)2 = r 2 }
Tutti i cerchi sono comunque
ottenibili dal cerchio di centro (0,0) e raggio 1, cioè di
equazione x2+y2=1, componendo  trasformazioni di
scala monometriche e traslazioni.
trasformazioni di
scala monometriche e traslazioni.
Le ellissi sono
le figure ottenibili dallo stesso cerchio componendo movimenti piani
e trasformazioni di scala anche non monometriche.
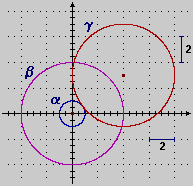 | 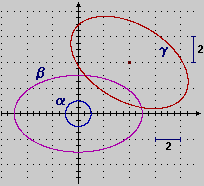 |
A lato (disegno a sinistra)
è illustrato come dal cerchio x2+y2=1 (α) è ottenibile il
cerchio β con una trasformazione di scala monometrica (di fattore 4) e, poi, il
cerchio γ con una traslazione (di vettore (4,3)). |
A destra è illustrata la generazione delle ellissi β (con una trasformazione di scala fattori 5 e 3) e, poi, γ (con una traslazione di vettore (4,4) seguita da una rotazione attorno a (4,4) di –30°).
|
Qualche figura con R
 Le figure di equazione
y = ax2 (con a numero reale diverso da 0) e
quelle ottenute da esse con movimenti piani vengono chiamate
Le figure di equazione
y = ax2 (con a numero reale diverso da 0) e
quelle ottenute da esse con movimenti piani vengono chiamate
 parabole.
Il disegno sotto a sinistra illustra una possibile generazione della parabola γ: la parabola y=2x2 (α) viene traslata con
Δx = –3, Δy = 1 (ottenendo β) e infine ruotata di 240° attorno alla
nuova posizione del vertice, cioè del trasformato del punto (0,0) della parabola iniziale.
parabole.
Il disegno sotto a sinistra illustra una possibile generazione della parabola γ: la parabola y=2x2 (α) viene traslata con
Δx = –3, Δy = 1 (ottenendo β) e infine ruotata di 240° attorno alla
nuova posizione del vertice, cioè del trasformato del punto (0,0) della parabola iniziale.
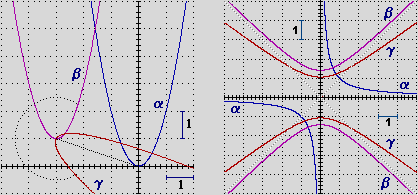
Le figure di equazione y = a/x
e tutte quelle ottenute da esse con movimenti piani vengono chiamate
iperboli equilatere. Sono tali α (y=1/x) e β (ottenuta da α con una rotazione di 45°) nel
disegno sopra a destra (altri esempi:  ,
,  ).
).
I due "rami" che compongono una iperbole equilatera tendono a spiaccicarsi su due rette perpendicolari.
Si chiamano iperboli anche le figure ottenute applicando
trasformazioni di scala non monometriche (la figura γ nel disegno, ottenuta da β con una trasformazione di scala che lascia immutate le x e moltiplica le y per 3/4);
queste figure tendono a spiaccicarsi su due rette non perpendicolari (le rette su cui tende a spiaccicarsi un'iperbole, o un altro tipo di curva, vengono chiamate asintoti).
Al posto di iperbole equilatera si usa spesso l'espressione iperbole rettangola, che meglio richiama il fatto che si tratta di una iperbole ad asintoti perpendicolari (nel caso dei poligoni l'aggettivo "equilatero" indica l'equaglianza dei lati, qui
la eguaglianza di due particolari segmenti che intervengono in un metodo per tracciare le iperboli che verrà discusso in una successiva voce).
Sia i cerchi, che le parabole e le iperboli equilatere sono figure tutte tra loro simili.
La figura a lato illustra la trasformazione di scala monometrica di fattore 2 di un cerchio e di una parabola. Le nuove figure sono meno "appuntite" ma hanno la stessa
forma.
La parabola y = ax2 si ottiene da y = x2 con la scala 1/a : al crescere
di a la parabola si rimpicciolisce (del resto più a è grande più y sale rapidamente al crescere di x, ossia più "stretta"
è la parabola). | 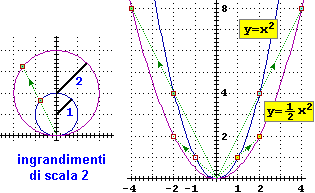 |
 Ellissi, parabole e iperboli sono tutte figure simmetriche, cioè
dotate di assi di simmetria: rette rispetto alle quali possono essere "ribaltate" senza cambiare aspetto, ossia rispetto alle quali sono simmetriche
di sé stesse [
Ellissi, parabole e iperboli sono tutte figure simmetriche, cioè
dotate di assi di simmetria: rette rispetto alle quali possono essere "ribaltate" senza cambiare aspetto, ossia rispetto alle quali sono simmetriche
di sé stesse [ trasformazioni geometriche].
trasformazioni geometriche].
Ogni retta è simmetrica (oltre che rispetto a sé stessa) rispetto a una qualunque retta ad essa perpendicolare.
Ogni segmento è simmetrico (oltre che rispetto alla retta a cui appartiene) rispetto alla retta perpendicolare che passa per il suo punto medio
(che viene in genere chiamata semplicemente asse del segmento). Ogni angolo è simmetrico rispetto alla bisettrice, ossia
alla retta che lo divide in due angoli di uguale ampiezza.
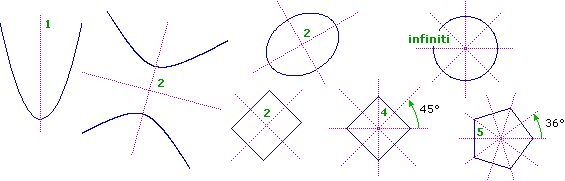
L'ellisse ha 2 assi di simmetria; se è un cerchio ne ha infiniti. L'iperbole ne ha 2, la parabola 1.
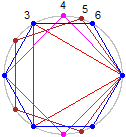
Il rettangolo e il rombo ne hanno 2; se sono quadrati ne hanno 4. I poligoni regolari, ossia con lati e angoli uguali, ne hanno tanti
quanti i lati: essi sono ottenibili a partire da una retta che sia bisettrice di un qualunque angolo mediante successive n-1 rotazioni ampie 360°/(2n),
se n è il numero dei lati. Vedi le figure sottostanti. I quadrangoli regolari sono i quadrati, i triangoli regolari
sono i triangoli equilateri (i quadrangoli equilateri non sono invece necessariamente regolari: possono essere rombi non quadrati).
A destra la figura illustra come i vertici di un poligono regolare stanno tutti su uno stesso cerchio. |
 |
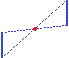
Segmenti, rettangoli, rombi, ellissi e iperboli sono tutte figure dotate di un centro di simmetria:
un punto rispetto al quale possono essere ruotate di 180° senza cambiare aspetto, ossia rispetto alle quali sono simmetriche
di sé stesse [ trasformazioni geometriche].
Lo sono anche tutti i poligoni regolari con un numero pari di lati. Ovviamente la presenza di una simmetria centrale non implica quella di
una simmetria assiale: i due segmenti a fianco sono simmetrici rispetto al punto evidenziato ma non hanno alcun asse di simmetria. trasformazioni geometriche].
Lo sono anche tutti i poligoni regolari con un numero pari di lati. Ovviamente la presenza di una simmetria centrale non implica quella di
una simmetria assiale: i due segmenti a fianco sono simmetrici rispetto al punto evidenziato ma non hanno alcun asse di simmetria. |
 |
 Una retta che
"tocca" il cerchio senza attraversarlo viene detta
tangente al cerchio. La parola
"tangente" deriva dal latino, in cui significava "che
tocca". La "funzione tangente" [ Una retta che
"tocca" il cerchio senza attraversarlo viene detta
tangente al cerchio. La parola
"tangente" deriva dal latino, in cui significava "che
tocca". La "funzione tangente" [ direzioni e funzioni circolari] deve il suo
nome al fatto che, ad es., tan(30°) può essere determinata
prolungando il versore di direzione 30° applicato in (0,0) fino
a intersecare la "retta tangente" in (1,0) al cerchio di
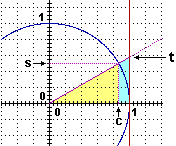
centro (0,0) e raggio 1: nella figura a lato, in cui è rappresentata la direzione 30°,
c e s sono rispettivamente il coseno e il seno di 30°; il fatto che il valore dell'ordinata t sia effettivamente
la tangente di 30° deriva dal fatto che il rapporto tra t e 1 (cioè t) è uguale al rapporto tra s e c,
cioè a sin(30°)/cos(30°) = tan(30°); o più semplicemente deriva dal fatto che t è la
pendenza della retta passante per (0,0) e inclinata di 30°: è la variazione verticale che corrisponde a una variazione orizzontale di 1. direzioni e funzioni circolari] deve il suo
nome al fatto che, ad es., tan(30°) può essere determinata
prolungando il versore di direzione 30° applicato in (0,0) fino
a intersecare la "retta tangente" in (1,0) al cerchio di
centro (0,0) e raggio 1: nella figura a lato, in cui è rappresentata la direzione 30°,
c e s sono rispettivamente il coseno e il seno di 30°; il fatto che il valore dell'ordinata t sia effettivamente
la tangente di 30° deriva dal fatto che il rapporto tra t e 1 (cioè t) è uguale al rapporto tra s e c,
cioè a sin(30°)/cos(30°) = tan(30°); o più semplicemente deriva dal fatto che t è la
pendenza della retta passante per (0,0) e inclinata di 30°: è la variazione verticale che corrisponde a una variazione orizzontale di 1. |
 |
La retta tangente è
perpendicolare al raggio che passa per il punto di contatto con il
cerchio.
Il concetto di retta
tangente può essere esteso ad altre figure.
Su ciò ci si soffermerà in successive sezioni.
 Se alle estremità di un'asta sono appesi due oggetti di diverso peso, per sostenere l'asta senza che ruoti non la impugno a metà, ma in un punto più vicino all'oggetto pesante: Se alle estremità di un'asta sono appesi due oggetti di diverso peso, per sostenere l'asta senza che ruoti non la impugno a metà, ma in un punto più vicino all'oggetto pesante: |  |
per equilibrare le opposte spinte alla rotazione esercitate dai due oggetti occorre tener conto che
esse non dipendono solo dalle masse dei due oggetti, ma dal  momento da essi esercitato, ossia anche dalla distanza delle loro forze-peso dal punto in cui tengo l'asta;
per ridurre l'effetto dell'oggetto più pesante devo ridurne la distanza dal centro di rotazione, ossia impugnare l'asta più vicino ad esso.
Il punto in cui tenere sospeso questo apparato (asta e due oggetti) in modo che i due momenti si bilancino viene detto centro di equilibrio.
Viene detto anche centro di massa o baricentro, ossia centro del peso (dal greco baros, che vuol dire
peso); infatti se sostengo l'apparato per questo punto devo contrastare solo la forza-peso complessiva,
senza sforzi per contrastare tendenze rotatorie: è come se si trattasse di un unico oggetto appeso in tale punto.
momento da essi esercitato, ossia anche dalla distanza delle loro forze-peso dal punto in cui tengo l'asta;
per ridurre l'effetto dell'oggetto più pesante devo ridurne la distanza dal centro di rotazione, ossia impugnare l'asta più vicino ad esso.
Il punto in cui tenere sospeso questo apparato (asta e due oggetti) in modo che i due momenti si bilancino viene detto centro di equilibrio.
Viene detto anche centro di massa o baricentro, ossia centro del peso (dal greco baros, che vuol dire
peso); infatti se sostengo l'apparato per questo punto devo contrastare solo la forza-peso complessiva,
senza sforzi per contrastare tendenze rotatorie: è come se si trattasse di un unico oggetto appeso in tale punto. |
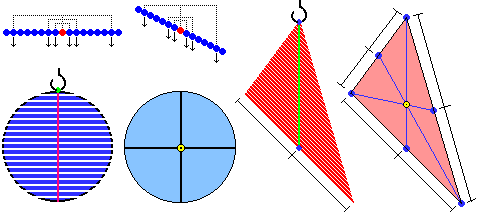
Consideriamo un'asta omogenea (ossia costituita da un solo tipo di materiale, con peso specifico che non varia da zona a zona), la cui forma possiamo approssimare con un segmento. È come se fosse composta da tante masserelle uguali. Se la sospendiamo per il punto medio, le masserelle sono a due a due disposte da parti opposte e ad uguale distanza da esso, producendo momenti di uguale intensità ma di direzione opposta; quindi annullano reciprocamente i loro effetti: l'asta non ruota e mantiene qualunque posizione in cui la disponga. Quindi il punto medio è il baricentro.
Consideriamo un disco omogeneo. Se lo appendo per un punto, esso ruota fino a che il diametro (e asse di simmetria) passante per tale punto si dispone verticalmente: infatti, in questa disposizione, è come se il disco fosse composto da tante asticciole orizzontali ciascuna delle quali è appesa per il punto medio e non esercita quindi alcuna spinta rotatoria. Se sospendo il disco per un altro punto dello stesso diametro la situazione non cambia: il diametro rimane disposto verticalmente. È come se la forza-peso agisse lungo il diametro, senza produrre momenti; quindi il baricentro, cioè il punto che si comporta come se la forza peso complessiva fosse applicata ad esso, deve stare su questo diametro. Lo stesso discorso si può fare per qualunque altro diametro: il baricentro è dunque un punto comune a tutti i diametri: è il centro del cerchio.
Nella illustrazione precedente è considerato anche il caso di una piastra omogenea di forma triangolare.
Se sospendo la piastra per uno dei vertici, essa ruota fino a che la retta passante per il vertice e per il punto medio del lato
opposto (retta che viene detta mediana - da non confondere con l'omonimo concetto statistico) si dispone verticalmente:
infatti è come se il triangolo fosse composto da tante asticciole parallele a tale lato ciascuna delle quali è appesa per il punto
medio e non esercita quindi alcuna spinta rotatoria. Analogamente al caso del cerchio, possiamo concludere che il baricentro deve stare su questa
retta, così come sulle altre due mediane, ossia le rette che congiungono gli altri due vertici ai lati a loro opposti.
Quindi per trovare il baricentro basta fare l'intersezione tra due di queste rette. Nota: sono chiamati mediane anche i segmenti che congiungono
i vertici del triangolo con i punti medi del lato opposto.
Il procedimento sperimentale sopra descritto (sospendere l'oggetto per due punti diversi, trovare l'intersezione delle due rette che in un caso e nell'altro passano per il punto di sospensione e sono verticali) funziona in generale, anche per oggetti tridimensionali. Ma, come abbiamo visto per il triangolo e il cerchio, nei casi in cui un oggetto è omogeneo e ha una forma semplice, il suo baricentro può essere determinato in base a considerazioni geometriche teoriche, prescindendo dal particolare materiale di cui è costituito. Data una figura, il punto che corrisponde alla posizione che avrebbe il suo baricentro se essa fosse costituita da materiale omogeneo, viene chiamata centroide in quanto generalizza il concetto di centro del cerchio (a volte viene chiamata più semplicemente centro o centro geometrico). In un oggetto composto da più tipi di materiali in genere baricentro e centroide non coincidono: in un disco composto da un semicerchio di plastica e un semicerchio di metallo il baricentro con coincide con il centro, ma è all'interno della parte metallica.
In analogia a quanto visto sopra per il cerchio, se una figura piana è
simmetrica il suo centroide sta sull'asse di simmetria. Ciò consente di individuare facilmente il centroide di ellissi, rettangoli, rombi, poligoni regolari e ogni altra figura piana che abbia almeno due assi di simmetria. È anche facile concludere, con un ragionamento simile a quello fatto in precedenza, che, quando una figura ha un
centro di simmetria C, questo ne è anche il centroide: infatti posso pensare la figura come composta da tante coppie di masserelle formate da una masserella e la sua simmetrica rispetto a C e tener conto che i loro effetti rotatori attorno a C si annullano reciprocamente.
Nel caso in cui una figura sia
scomponibile in altre figure, per determinarne il centroide si può procedere nel modo illustrato sotto:

| La figura rappresentata in A è scomponibile in rettangoli (uno di area doppia) nel modo illustrato in B, in cui sono evidenziati anche i centroidi dei due rettangoli. Il centroide dell'intera figura deve stare sulla retta che congiunge questi due centroidi (vedi C), in quanto se avessi due masse concentrate in tali punti il centro di equilibrio starebbe sul segmento che li congiunge. E deve essere più vicino alla massa maggiore (ossia al centroide del rettangolo di area doppia), in modo che i momenti delle due masse rispetto ad esso si bilancino: le distanze devono essere inversamente proporzionali ai "pesi", ossia la distanza del centroide dal primo punto deve essere doppia di quello dal secondo: vedi D. In definitiva il centroide sta sul bordo della figura, come illustrato in E. |
In questo caso si poteva procedere anche come illustrato in F: scomporre la figura in due figure di eguale area e trovare il punto medio dei loro centroidi (essendo uguali i "pesi" devono essere uguali anche le distanze).
Si osservi che se si allungasse un po' verso l'alto la nostra figura
(ad es. aggiungendo 2 quadretti in alto a sinistra) il suo centroide cadrebbe fuori dalla figura stessa.
Del resto anche il nostro baricentro è spesso fuori di noi: se siamo seduti è all'interno
dell'angolo formato dal tronco e dalle cosce, nel fare una gara di salto in alto (se siamo bravi) facciamo in modo
che il nostro baricentro non superi l'asticella (cerchiamo di inarcarci in modo da mantenere il baricentro basso e
dover compiere meno lavoro per vincere il nostro peso), … |
 |
 |
Per affrontare problemi in cui c'è da calcolare il baricentro (o centro di massa) di più oggetti di masse diverse è molto
comodo determinare le coordinate di esso facendo riferimento ad un sistema di assi e calcolando i momenti dei diversi oggetti dotandoli
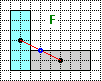
di segno. Precisiamo queste considerazioni facendo riferimento alla situazione illustrata a fianco, in cui supponiamo che le due masse siano
di 1 kg (quella a sinistra) e di 2 kg (quella a destra).
Fissato un generico punto (h,k), si calcola il momento del primo oggetto rispetto a x=h, pensandolo proiettato sull'asse x, facendo il prodotto tra
la differenza della sua ascissa da h e la sua massa: (1−h)·1 kg. Si fa lo stesso per l'altro oggetto:
(4−h)·2 kg. Si calcolano analogamente i momenti rispetto a y=k pensando gli oggetti proiettati sull'asse y:
(3−k)·1 kg, (0−k)·2 kg.
Si prende come baricentro il punto (h,k) per cui la somma dei momenti dei due oggetti è nulla:
(1−h)·1 kg + (4−h)·2 kg = 0 → 1·1 kg+4·2 kg + h·(1+2) kg = 0 →
h = (1·1 kg+4·2 kg)/((1+2) kg) = 9/3 = 3
Analogamente si ottiene: k = (3·1 kg+0·2 kg)/((1+2) kg) = 3/3 = 1.
Abbiamo ritrovato il punto (3,1).
|
In generale, se ho le masse m1, m2, m3, … aventi ascisse x1, x2, x3, … e ordinate y1, y2, y3, …,
il baricentro (h,k) è:
h = (x1·m1 + x2·m2 + x3·m3 + …) / (m1 + m2 + m3 + …),
k = (y1·m1 + y2·m2 + y3·m3 + …) / (m1 + m2 + m3 + …).
Spesso al posto di "centro di massa" si usa "centro di gravità", che è definito in maniera analoga facendo riferimento ai pesi
invece che alle masse; nella pratica, per corpi di dimensioni non enormi, in cui l'accelerazione di gravità non varia, i due concetti coincidono
(vedi). |
 | Se una figura ha dei buchi il centroide si calcola in modo analogo.
Nel caso dell'unione di due figure di aree A1 ed A2 e centroidi C1 e C2 l'ascissa xC del centroide C è tale che
xC·(A1+A2) = xC1·A1+xC2·A2; cosa analoga ho per l'ordinata.
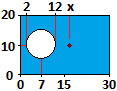
Nel caso a lato, in cui ho una figura di area U pari ad una figura di area U2 da cui è stata tolta una figura di area U1 (U=U2−U1),
indicati con C, C1 e C2 i centroidi, ho xC·(U2−U1) = xC2·U2−xC1·U1.
Nel caso raffigurato yC = yC1 = yC2. Per le ascisse:
x·(30·20−π5²) = 15·30·20 − 7·π5², da cui
x = (15*600-7*pi*5^2)/(600-pi*5^2) = 16.20492.
|
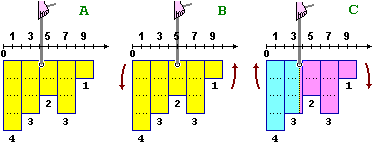
 NOTA 1. Se ho un oggetto di lamiera o di compensato dalla forma di istogramma, dove devo praticare un foro a cui appenderlo in modo che la "base" rimanga orizzontale come nella sottostante figura A? NOTA 1. Se ho un oggetto di lamiera o di compensato dalla forma di istogramma, dove devo praticare un foro a cui appenderlo in modo che la "base" rimanga orizzontale come nella sottostante figura A?
Devo fare in modo che le spinte rotatorie a sinistra e a destra del foro si bilancino, quindi non posso disporlo al centro della base, come nella figura B, in quanto la colonna all'estremità sinistra "pesa" di più della colonna all'estremità destra, e l'istogramma ruoterebbe. |
|
Non posso disporlo neanche nel punto della base per cui passa la perpendicolare che taglia in due parti di eguale area (6 quadretti e mezzo) l'istogramma, come in C: l'istogramma ruoterebbe in senso opposto in quanto la parte a destra è più larga, ha un baricentro che dista da tale punto più di quanto dista quello dell'altra parte, e quindi, pur avendo lo stesso peso, produce un momento maggiore.
|  |
Queste considerazioni ne richiamano altre svolte alla voce  valori medi (2) sulla distinzione tra media e mediana. In effetti, come si può intuire, il foro deve essere praticato in corrispondenza della posizione che corrisponde alla media della distribuzione rappresentata dall'istogramma. In altre parole, la media è la ascissa del baricentro dell'istogramma. valori medi (2) sulla distinzione tra media e mediana. In effetti, come si può intuire, il foro deve essere praticato in corrispondenza della posizione che corrisponde alla media della distribuzione rappresentata dall'istogramma. In altre parole, la media è la ascissa del baricentro dell'istogramma. |
Vediamone la dimostrazione:
indichiamo con x la coordinata (rispetto al sistema di riferimento tracciato) del foro e cerchiamo di descrivere con un'equazione (che poi cercheremo di risolvere rispetto a x) le condizioni di equilibrio. Valutiamo il peso in quadretti. Evitando di esplicitare le unità di misura, possiamo dire che la colonna posizionata in 1 esercita rispetto al foro il momento (= distanza per peso) (x-1)·4. Quella posizionata in 9 esercita il momento (9-x)·1. Eguagliando la somma dei momenti prodotti dalle colonne a sinistra del foro e quello prodotto da quelle a destra abbiamo: |
(x–1) · 4 + … = … + (9–x) · 1, da cui:
(x–1) · 4 + … – (… + (9–x) · 1) = 0
(x–1) · 4 + … + … + (x–9) · 1 = 0, cioè
(x–1) · 4 + (x–3) · 3 + (x–5) · 2 + (x–7) · 3 + (x–9) · 1 = 0
x · (4 + 3 + 2 + 3 + 1) = 1·4 + 3·3 + 5·2 + 7·3 + 9·1
x = (1·4 + 3·3 + 5·2 + 7·3 + 9·1) / (4 + 3 + 2 + 3 + 1) = 4.077. |
| [che corrisponde alla formula che esprime la media artimetica] |
Questa interpretazione "fisica" spiega perché la media aritmetica, quando si dispone di valori dotati di frequenza ( valori medi (1)), viene spesso chiamata media pesata. valori medi (1)), viene spesso chiamata media pesata. |
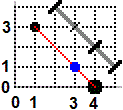
 NOTA 2. Se conosco le coordinate dei punti P1, P2 e P3 in cui sono concentrate (o hanno baricentro) tre masse uguali, per determinare il baricentro complessivo posso fare la media di tali coordinate: NOTA 2. Se conosco le coordinate dei punti P1, P2 e P3 in cui sono concentrate (o hanno baricentro) tre masse uguali, per determinare il baricentro complessivo posso fare la media di tali coordinate:
x baricentro = (x1+x2+x3) / 3
y baricentro = (y1+y2+y2) / 3
Infatti (vedi figura a lato) il baricentro del complesso delle prime due masse sta nel punto medio dei loro baricentri, che ha come x la media delle x di essi. La x del baricentro complessivo si ottiene facendo la media pesata della x di questo baricentro (con peso 2) e la x della terza massa (con peso 1): il contributo del complesso delle due prime due masse è doppio di quello della terza. Svolgendo i calcoli e semplificando si ottiene che la x del baricentro complessivo è la media delle x dei tre baricentri.
Condiderazioni analoghe valgono per la y. | 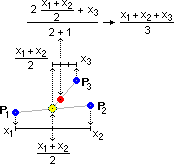 |
|
Il ragionamento può essere esteso a una quantità qualunque di masse tra loro uguali. |
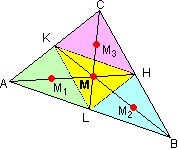
 NOTA 3. Se conosco le coordinate dei vertici di un triangolo ABC, per determinarne il centroide posso fare la media di esse: NOTA 3. Se conosco le coordinate dei vertici di un triangolo ABC, per determinarne il centroide posso fare la media di esse:
xcentroide = (xA+xB+xC) / 3
ycentroide = (yA+yB+yC) / 3
Infatti se congiungo i punti medi dei lati suddivido il triangolo in 4 triangolini uguali e, quindi, di "massa" uguale: vedi figura a destra.
Il centroide (o baricentro) M deve dunque coincidere col baricentro di 3 masse uguali posizionate nei baricentri M1,
M2 e M3 dei tre triangolini esterni (l'altro, come è facile concludere, ha baricentro in M).
Per quanto visto nella nota precedente, le coordinate di M sono la media delle coordinate di M1, M2 e M3.
Ma, poiché CM3 è uguale alla metà di CM (essendo 1/2 il fattore di scala tra traingolo e triangolini), M3
sta a metà tra C e M; analogamente M2 e M1 stano a metà tra B e M e tra A e M.
Quindi la media delle coordinate di M1, M2 e M3 coincide con la media delle coordinate di A, B e C. |
 |
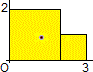
Per determinare il centroide di un poligono P posso suddividerlo in triangoli, o in altri poligoni, P1, …, Pn, trovare i centroidi di questi e poi
prendere come centroide di P il baricentro dei centrodi di P1, …, Pn assumendo come massa di ciascuno di essi la sua area.
Ad es. nel caso a fianco il centroide del primo quadrato è (1,1); quello del secondo è (2.5,0.5); la ascissa del centroide dell'intera figura è
(1·4+2.5·1)/(4+1) = 6.5/5 = 1.3; l'ordinata è (1·4+0.5·1)/(4+1) = 4.5/5 = 0.9.
L'argomento della determinazione del centroide di un poligono viene ripreso alla fine della voce  area area
|
 |
Esercizi: testo1 e soluzione, testo2 e soluzione, testo3 e soluzione, testo4 e soluzione, testo5 e soluzione, testo6 e soluzione
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 figure della
figure della  geometria piana euclidea.
geometria piana euclidea. La semiretta di
origine A e direzione α è l'insieme
dei punti che possono essere ottenuti da A con traslazioni di
La semiretta di
origine A e direzione α è l'insieme
dei punti che possono essere ottenuti da A con traslazioni di
 direzione α. Intuitivamente, è la figura generata da un punto che parte da una posizione fissata e prosegue (oltre ogni limite) in una direzione fissata.
direzione α. Intuitivamente, è la figura generata da un punto che parte da una posizione fissata e prosegue (oltre ogni limite) in una direzione fissata. (solo se A e B coincidono, ossia se il segmento si riduce ad un punto, la lunghezza di AB è nulla e, ovviamente,
la direzione da A a B non è fissata).
Il suo punto medio, generalizzando quanto visto per gli
(solo se A e B coincidono, ossia se il segmento si riduce ad un punto, la lunghezza di AB è nulla e, ovviamente,
la direzione da A a B non è fissata).
Il suo punto medio, generalizzando quanto visto per gli  intervalli,
è il punto di esso equidistante dagli estremi, ossia
intervalli,
è il punto di esso equidistante dagli estremi, ossia 



 ax+b
ax+b

























