Funzione (2)

  Possiamo generalizzare il concetto di funzione a input e output numerici [ funzione 1], in modo da inglobare altri esempi di funzione incontrati in varie sezioni precedenti (la distanza, che a due punti associa un numero; le trasformazioni geometriche, che associano punti a punti; gli operatori logici, che trasformano condizioni in condizioni; …).
    Possiamo dire che in ogni caso abbiamo l'accoppiamento in modo non ambiguo di un input a un output (input → output), nel senso che se si ripete lo stesso input non si può ottenere un output diverso. Ecco come si può tradurre questa idea sotto forma di definizioni un po' più formalizzate:

Dati due insiemi I e O di oggetti matematici, una funzione a input in I e output in O è
un insieme F di coppie a, b con a ∈ I e b ∈ O tale che per ogni a in I accada uno dei due seguenti fatti:

[con "a  b", o con "a ∼>  b", o "a → b", indichiamo "la coppia a, b", ossia l'accoppiamento di a a b]

  (1)  c'è un unico oggetto b di O tale che a → b stia in F (ossia per a c'è un solo accoppiamento);
      F(a) è definito e b è l'output corrispondente tramite F all'input a;
      si scrive  F(a) = b  o  F: a →  b

  (2)  non c'è alcun oggetto b di O tale che a → b stia in F (ossia per a non ci sono accoppiamenti).
      F(a) è indefinito ovvero all'input a F non associa alcun output.

L'insieme degli a per cui F(a) è definito si dice dominio (o insieme di definizione) di F.

Ad es. nel caso della divisione (che avevamo considerato come una funzione a 2 input numerici) posso prendere come  I  l'insieme delle coppie x,y di numeri reali, ossia considerare i 2 input come un unico input: un oggetto costituito da una sequenza di 2 numeri.
Il dominio non è costituito da tutte queste sequenze, ma solo da quelle con y 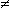0 (quelle per cui si può calcolare x/y).

Se il dominio di F è finito, F può essere descritta elencando in una tabella tutte le possibili coppie "input → output". In altri casi F può essere descritta con un procedimento di calcolo che consente di determinare per ogni input l'output corrispondente. In altri casi ancora non è possibile neanche questo tipo di descrizione. Ecco alcuni esempi per ciascuna di queste tipologie:

I (km)  O (€) 0 1.2 1 1.2 ... ... 200 3.2	I O  V   V  V  V   F   F   F   V   F   F   F   F		I O "ba" "co" "baco" "ba" "cio" "bacio" "r" "oro" "roro" ... ... ...	I O 0, 1 0.5 2, 3.5 2.75 1.2, 1.3, 1.2, 1.1 1.2 ... ...	I O  -1   1   0   0   0.3   0.9   ...   ...
tariffe del bus	significato di AND		concatenazione	media	x → x2
funzioni rappresentabili completamente mediante tabelle			funzioni non rappresentabili completamente mediante tabelle

Quando la funzione F è descritta con una formula, come F(x) = 3/x, in genere si prende come dominio l'insieme di tutti gli x per cui il termine impiegato (3/x nell'esempio) è definito (tutti i numeri diversi da 0), ma a volte si esplicita un dominio più piccolo:  se 3/x rappresenta come suddividere una spesa di 3 € tra x persone si esclude che x sia negativo, ed anche che x non sia intero, ossia si prende come dominio l'insieme dei numeri interi positivi.     Al posto di "funzione" si usa spesso il termine "applicazione"; noi non useremo mai questa parola, in genere usata quando si ha a che fare con funzioni tra oggetti non numerici.

funzione non rappresentabile completamente né con una tabella né con un procedimento di calcolo

    Spesso si parla anche di funzioni a più input o di funzioni a più output per intendere funzioni che hanno come input o come output invece che un unico oggetto una coppia o una n-upla (con n numero intero maggiore di 1) di oggetti matematici. Invece di funzioni a più input si parla anche di funzioni di più variabili.  Se, usando questo linguaggio, consideriamo la funzione media, che ad un insieme di dati associa il loro valore medio, possiamo dire solo che è una funzione ad 1 o più input, in quanto possiamo fare la media di una quantità qualunque di numeri.

    Questa definizione di funzione risale al 1834 (formulata da Nikolai Lobachevsky e, indipendentemente, 3 anni dopo, da Peter Gustav Lejeune Dirichlet).  A noi sembra una definizione ovvia, ma all'epoca non era così.  Infatti fino ad allora si consideravano solo funzioni ad 1 input ed 1 output definite su intervalli di numeri reali che rappresentavano movimenti di oggetti o fenomeni simili, che si supponeva variassero con continuità, che avessero un grafico senza salti o punti angolosi.  È in quegli anni che le applicazioni della matematica si estesero a nuovi campi che richiesero l'uso di un concetto più generale di funzione.  Non a caso la stessa definizione fu messa a punto da due persone indipendentemente e più o meno contemporaneamente.

  A volte invece di «coppia x,y» si parla di «coppia ordinata x,y» per specificare che non ci riferisce all'insieme {x,y} ma alla sequenza x,y, che ha x come 1° elemento e y come 2° elemento.
In genere invece di "coppia x,y" si scrive "(x,y)", non solo quando x e y sono impiegate come coordinate di un punto, oppure "x  y", o "x → y", specie quando si intende esprimere l'associazione di y a x.

Se fisso un particolare insieme di input A per cui la funzione F è definita, l'insieme { F(x) / x ∈ A } dei corrispondenti output viene indicato F(A) e chiamato insieme immagine di A mediante F (o più in breve, se è chiaro quale sia il dominio, immagine di F).    Nel caso illustrato a lato, per A = (–1, 1) si ha F(A) = [0,1):  1 non appartiene a F(A) in quanto è immagine di –1 e 1 che non appartengono ad A. Nota. La notazione F(…) è ambigua poiché è usata anche per indicare un singolo output, ma in genere dal contesto si capisce in che senso è impiegata.   Una figura piana H è interpretabile come grafico di una funzione (a 1 input e 1 output numerici) quando per ogni retta r parallela all'asse y accade che:   •  r interseca H in un unico punto   o:   •  r non interseca H in alcun punto.

Le relazioni rappresentate al centro e a destra ad alcuni valori di x associano più di un valore di y: non sono funzioni come lo è invece quella rappresentata a sinistra.

 

  Nel caso delle funzioni a input e output in R alcune composizioni sono interpretabili geometricamente:

traslazione che porta gli assi sui nuovi asintoti

traslazione che porta il vertice della parabola nel nuovo vertice

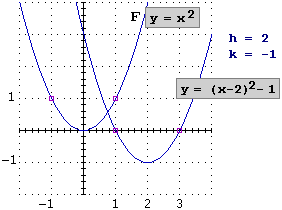	x  → F(x– h)+k ha come grafico il grafico di F traslato con passi Δx = h, Δy = k (le x in cui eventualmente interseca l'asse orizzontale sono le soluzioni di F(x) = – k) Nota. Traslare orizzontalmente di h corrisponde a sostituire x con x–h: spostare il grafico a destra vuol dire "ritardare" l'effetto, ossia decrementare l'input [viceversa, spostare il grafico a sinistra vuol dire anticipare l'effetto, ossia incrementare l'input: x → F(x+h) ha il grafico di F traslato di Δx = –h].
	Grafici con R: uno, due, tre
	x → k·F(x) ha grafico ottenibile da quello di F mediante una trasformazione di scala che moltiplica per k le ordinate (i due grafici intersecano l'asse x negli stessi punti)
	x → – F(x) ha grafico ottenibile da quello di F con un ribaltamento attorno all'asse x (i due grafici intersecano l'asse x negli stessi punti)

Applicando la moltiplicazione o il cambio segno invece che a F(x) all'input x gli effetti sono diversi: x → F(k·x) ha grafico ottenibile da quello di F mediante una trasformazione di scala che divide per k le ascisse; x → F(– x) ha grafico ottenibile da quello di F con un ribaltamento attorno all'asse y (in entrami i casi le intersezioni con l'asse y sono le stesse che per F)

Esercizio   (in una nuova finestra)

 

Le funzioni che a input diversi fanno corrispondere output diversi vengono dette funzioni iniettive.     Casi particolari di funzioni iniettive sono le funzioni crescenti e decrescenti:

una funzione (a input e output in R) è detta crescente in un intervallo I se:			porzione del grafico di una funzione crescente in (–, A] e in [B, ), decrescente in [A, B]
	è definita in I e all'aumentare dell'input (preso in I) l'output aumenta [presi x1 < x2 in I si ha F(x1) < F(x2)]
decrescente in I se:
	è definita in I e all'aumentare dell'input (preso in I) l'output diminuisce [presi x1 < x2 in I si ha F(x1) > F(x2)]

Abbiamo fatto ricorso, implicitamente, a questi concetti affrontando alcune questioni di calcolo approssimato [ calcolo approssimato]

Nota 1.  Quando una funzione F è crescente o presenta dei tratti in cui è costante ed eventuali altri in cui cresce, ossia quando presi x < y si ha F(x) ≤ F(y), come la funzione rappresentata a sinistra (che è costante nell'intervallo (p,q) e crescente altrove) si usa dire che F è crescente in senso lato  (alcuni usano dire che è non decrescente, ma si tratta una espressione ambigua, contradditoria rispetto all'interpretazione usuale di "non": si potrebbe intendere che è "non" decrescente una funzione che oscilla).  Qualcuno per indicare che una funzione è crescente usa l'espressione strettamente crescente, per rafforzare il significato e chiarire che non intende riferirsi al senso lato. Alcuni usano crescente per indicare crescente in senso lato.  Può essere utile, quando ci si esprime in un contesto in cui non siano chiare le convenzioni adottate, affiancare all'aggettivo crescente (o decrescente) la specificazione se sia da intendere "in senso stretto" o "in senso lato".

Nota 2.  La funzione rappresentata graficamente a lato nel suo dominio, l'intervallo [1,5], non è nè crescente né decrescente, ma un po' cresce e un po' decresce. Ciononstante è iniettiva in quanto ogni output proviene da un solo input (ad es. 2 è l'output di 2 mentre 3.5 è l'output di 2.5); infatti ogni retta orizzontale interseca il grafico in al più un punto. Esercizio (e soluzione)

  Nel caso delle funzioni iniettive, poiché ogni output può corrispondere a un solo input, possiamo anche fare l'associazione inversa: all'output associare senza ambiguità l'input. In pratica, nel caso del grafico di una funzione a input e output in R, se scambiamo le x con le y, cioè se ribaltiamo il grafico attorno alla retta y=x (vedi la figura seguente, in cui sono rappresentate la funzione non iniettiva x → x² e quella iniettiva x → x³), otteniamo il grafico di una relazione che è ancora una funzione. Ribaltare il grafico (vedi figura C a destra) è come vedere il grafico in trasparenza dal retro del foglio, ruotato in modo che l'asse y sia disposto orizzontalmente.
    Le funzioni inettive ammettono dunque una funzione inversa in tutto il loro dominio.

I grafici precedenti suggeriscono altre osservazioni sull'interpretazione geometrica dei grafici delle funzioni:
•  x → x² (e così x → x⁴, x → x⁶, …, x → 1/x², …) hanno grafico simmetrico rispetto all'asse y (infatti a 1 e –1, a x e a –x corrisponde lo stesso output) e, più in generale, il grafico di x → (x–h)^N, se N è un intero pari, è simmetrico rispetto alla retta x=h; per estensione, tutte le funzioni (da R in R) che hanno grafico simmetrico rispetto all'asse y vengono dette funzioni pari;
•  x → x, x → x³ (e così x → x⁵, x → x⁷, …, x → 1/x, …) hanno grafico simmetrico rispetto al punto (0,0) (infatti 1 e –1, x e –x hanno output uguali in valore assoluto e di segno diverso) e, più in generale, il grafico di x → (x–h)^N se N è un intero dispari, è simmetrico rispetto al punto (h,0); per estensione, tutte le funzioni che hanno grafico simmetrico rispetto a (0,0) vengono dette funzioni dispari.

 Nota.  Invece di dominio di una funzione F si usa parlare anche di insieme di partenza di F; qualcuno riserva tale espressione per tutto l'insieme degli input I, inclusi gli input x per i quali F(x) non è definito.  Se D è il dominio di F, invece di immagine di D mediante F (l'insieme degli output di F) si parla anche di insieme dei valori (o di variabilità) di F; in inglese si parla anche di range di F. Qualcuno chiama tale insieme codominio di F, ma in genere si riserva tale espressione a tutto l'insieme O dei potenziali output (per intenderci, nel caso della funzione a input e output reali x → x², chi facesse tale uso chiamerebbe codominio [0,), mentre dovrebbe essere indicato in tal modo tutto R): se non è chiaro il senso con cui usiamo questa espressione, è meglio non usarla.
    Osserviamo che gli input e gli output di una funzione potrebbero essere oggetti matematici qualunque. Anche nel software in genere viene chiamata function qualunque associazione di input ad output; ad esempio in R posso definire come "funzione" il procedimento che, fissato un intervallo I, associa ad ogni funzione F il grafico di essa in I: gli input sono funzioni, gli output sono grafici.

Esercizi:      

 altri collegamenti     [nuova pagina]