Insiemi infiniti
L'infinitamente grande e l'infinitamente piccolo
Scheda 1
Si usano spesso, nel linguaggio comune e in varie discipline (in Fisica, Filosofia, Astronomia, …) termini come "infinito" e "infinitesimo".
Ma, con esattezza, che cosa vogliono dire?
E, quando li si usa in Matematica, viene dato a loro lo stesso significato?
Quali calcoli e altre manipolazioni matematiche si possono fare con questi "oggetti" infiniti o infinitesimi?
Quali cautele occorre prestare nel lavorare con essi?
Nel "percorso" che stiamo per intraprendere, di cui questa scheda è la prima tappa, cercheremo di precisare questi interrogativi e tenteremo di dar loro
qualche prima risposta.
1. L'«infinito» nel linguaggio comune e non
| In un vocabolario per l'aggettivo infinito troviamo questi tre significati: | 1 senza limiti
2 non determinato, non definito
3 innumerevole. |
| [1] Secondo voi, nelle frasi a lato l'aggettivo o il sostantivo "infinito" che vi compare a quale di queste tre accezioni è più vicino? |
- Infiniti ringraziamenti.
- Quel film era una noia infinita.
- Il tempo secondo me è infinito.
- Il modo infinito è spesso usato come sostantivo.
- Il tuo programma va avanti all'infinito, controlla le condizioni che hai messo nel comando "if-then-else".
|
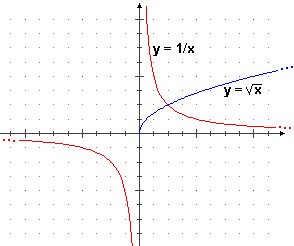
[2] Viene chiamato "infinito" il simbolo ∞ che
si usa nella indicazione di alcuni intervalli di numeri,
come nei seguenti esempi, riferiti ai grafici a fianco.
Secondo voi, "infinito" in questo caso a quale dei tre significati è più vicino?
- la funzione √ ha [0, ∞) come dominio
- la funzione reciproco (che a x associa 1/x) ha (–∞,0) U (0,∞) come dominio
|  |
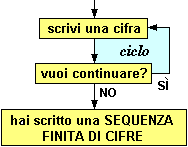 |
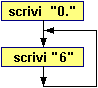
Un numero naturale è formato da una sequenza finita di cifre. Scrivo una cifra; se voglio scrivo a destra un'altra cifra; e così via. Quando mi fermo posso esprimere con una parola il numero che ho scritto. Il diagramma a sinistra illustra questo procedimento. |
[3] Usa il diagramma scrivendo come prima cifra 2, poi 0, poi 2, … (alternando 2 e 0) e percorri il ciclo passando per la freccia "sì" in tutto quattro volte. Scrivi in lettere il numero che hai generato.
________________________________________ |
Quando dico che l'insieme dei numeri naturali pari (i numeri 0, 2, 4, 6, 8, 10, 12, …) è infinito intendo dire che i numeri pari sono in quantità "innumerevole", che non riesco a contarli tutti.
Anche l'intervallo di numeri reali [0, ∞) è un insieme infinito: basti pensare che contiene l'insieme dei numeri pari. È anche un intervallo illimitato:
comunque prenda un punto sull'asse x a destra dell'origine, ne posso tracciare uno a distanza doppia dall'origine, uno a distanza tripla, …: non esiste distanza oltre la quale non possa andare (eventualmente aggiungo un altro foglio, se non mi basta il pezzo di asse x che ho disegnato sul foglio che ho a disposizione).
Anche (-∞, 0] è illimitato: comunque prenda un punto a sinistra dell'origine, ne posso trovare alla sua sinistra uno a distanza doppia, tripla, … . Possiamo dire che [0, ∞) è superiormente illimitato e che (-∞, 0] è inferiormente illimitato.
[4] Il diagramma a destra illustra il significato di numero reale. Usalo per generare un particolare numero reale nel seguente modo:
– non scrivere "–",
– scrivi "41",
– scrivi "." e poi
– percorri il ciclo scrivendo via via la cifra finale dei secondi che di volta in volta leggi sul tuo orologio.
[quando sei stanco fermati]
• Puoi esprimere con una parola il numero che stai scrivendo?
• Quanti sono i numeri reali che iniziano con "41."?
• L'intervallo di numeri reali [41, 42] è limitato o illimitato? finito o infinito? | 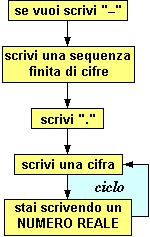
|
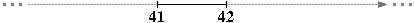 |
2. L'infinito in matematica
| In matematica il termine infinito viene usato in molti modi; ad es.:
|
- per indicare gli estremi di un intervallo di numeri illimitato, senza confini invalicabili ("i numeri compresi tra 0 e infinito")
- per indicare un processo che si sviluppa stato dopo stato senza fine ("quel programma contiene un ciclo infinito")
- per indicare un insieme formato da una quantità innumerevole di oggetti ("i numeri reali compresi tra 0 e 1 sono infiniti")
|
Sono significati simili ai significati 1 e 3 del vocabolario della lingua italiana considerato nella prima sezione.
E sono significati abbastanza collegati tra di loro:
• quando dico che un insieme è infinito
(significato C) intendo dire che il
procedimento di conta dei suoi elementi, "1, 2, 3, …", è infinito (significato B).
• un intervallo di numeri reali del tipo [k, ∞)
(significato A) è sicuramente infinito (significato C),
in quanto altrimenti avrebbe un ultimo elemento,
che costituirebbe un confine oltre il quale non si potrebbe andare. |
Ma questi legami tra i diversi significati e la nostra intuizione, che è
abituata a ragionare sul "finito", a volte ci possono trarre in inganno.
Abbiamo visto ad esempio che l'intervallo di numeri reali [41, 42],
così come [0, 1]
e ogni intervallo che ha per estremi numeri reali diversi,
pur essendo limitato, è infinito:
presi comunque un tot di numeri che stanno nell'intervallo ne posso sicuramente trovare uno nuovo,
che da un certo punto in poi abbia uno sviluppo delle cifre diverso dagli altri.
Del resto, presi comunque due numeri x e y che stanno nell'intervallo, posso,
proprio perché si tratta di un intervallo,
trovarne un terzo compreso strettamente tra essi; basta, ad esempio prenderne la media: (x+y)/2.
Vediamo qualche altro problema connesso all'uso dell'infinito.
3. Processi infiniti
[5] Esegui "a mano" il risultato della divisione tra 6 e 9. Quale è il numero reale che ne è il risultato esatto?
Prova a moltiplicare "a mano" per 3 questo numero; come fai? che cosa ottieni?
(1)
6 | 9
|————
| |
(2)
6 | 9
|————
| 0 |
(3)
6 | 0
0 |————
| 0 |
(4)
6 | 9
-0 |————
—— | 0
6 |
(5)
6 | 9
-0 |————
—— | 0.6
60 |
(6)
6 | 9
-0 |————
—— | 0.6
60
-54
———
6 |
(7)
6 | 9
-0 |————
—— | 0.66
60
-54
———
60 |
ecc.
(7)—>(8) come (5)—>(6)
(8)—>(9) come (6)—>(7) |
[6] Batti un numero positivo qualunque sulla tua calcolatrice e poi, schiaccia ripetutamente il tasto per il calcolo della radice quadrata. Che cosa osservi? Secondo voi, si può sintetizzare con una formula quanto avete osservato?
4. Insiemi infiniti
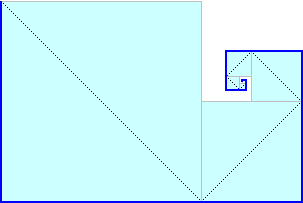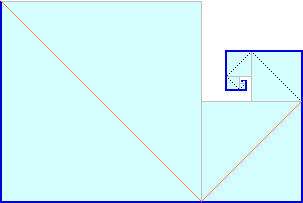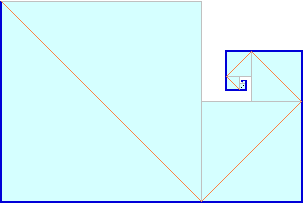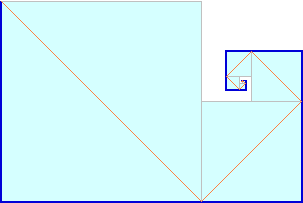
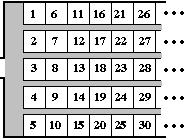
[7] Siamo nella città sede delle prossime Olimpiadi.
Gli hotel Jolly, Star ed Eden, identici, hanno tutti e tre una infinità di stanze che sono numerate
1, 2, 3, … .
• Il proprietario dello Star pensa: «Arriveranno molti turisti;
attrezzo ad albergo anche il piccolo edificio a fianco: se completo l'edificio principale avrò
altre 10 stanze per altrettanti nuovi clienti»
• Quello dell'Eden fa le cose in grande: «Costruisco un edificio uguale al precedente: sarò
in grado di raddoppiare il numero dei clienti ospitati»
• Il proprietario del Jolly, invece pensa così: «Che stupidi! anche con l'hotel al completo
si possono sempre operare dei cambiamenti di stanza degli ospiti e liberare posti per i nuovi
arrivati»
Sotto vedete raffigurati i tre hotel dopo i lavori di ampliamento. Il Jolly è praticamente
contenuto strettamente sia nello Star che nell'Eden.
Secondo voi ha ragione il suo proprietario a sostenere che potrà ospitare
la stessa quantità di clienti? Come potrebbe fare?
Un problema a cui pensare a casa
|
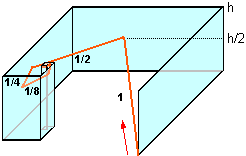
[8]
Un raggio di luce, leggermente inclinato rispetto al piano orizzontale,
entra nella infinita "spirale" di specchi raffigurata sotto (a destra è vista dall'alto).
Il primo tratto rettilineo percorso nella spirale è lungo 1 m, il secondo è lungo 1/2 m,
il terzo 1/4 m, il quarto 1/8 m, ….
Secondo te prima o poi il raggio di luce esce da questo "percorso guidato"? Con
quale eventuale direzione? |
 |
 |
L'infinitamente grande e l'infinitamente piccolo
Scheda 2
1. Numeri a infinite cifre, ovvero misure infinitamente precise
Se eseguo la divisione di 6 per 9 ottengo 0.666… con infiniti "6", o, meglio, riuscirei ad ottenerlo se
potessi vivere in eterno, avessi a disposizione infinita carta, ecc.
Nella scheda 1 (quesito 5) abbiamo provato a moltiplicare 0.666… per 3, ma non è stato facile farlo:
• dalla cifra più a destra di tutte non posso partire in quanto una tale cifra non c'è;
• se prendo solo 0.66 ottengo 0.66·3 = 1.98;
• se prendo 0.666 ottengo 0.666·3 = 1.998
• Come posso prendere in esame tutti i "6"?
|
 |
Posso osservare che, aumentando il numero dei "6" presi in considerazione, ottengo.
0.6666·3 = 1.9998, 0.66666·3 = 1.99998, 0.666666·3 = 1.999998, …
ossia che il risultato tende a stabilizzarsi su 1.999….
Ragionando sul fatto che dire che 0.6 è un troncamento di un numero significa che questo è compreso tra 0.6 e 0.7,
dire che 0.67 è un altro troncamento significa che il numero sta tra 0.66 e 0.67; …,
potrei vedere le cose anche in questo modo:
|
0.6 ≤ 0.666… ≤ 0.7 | quindi | 1.8 =0.6·3 ≤ 0.666…·3 ≤ 0.7·3= 2.1 |
|
0.66 ≤ 0.666… ≤ 0.67 | quindi | 1.98 =0.66·3 ≤ 0.666…·3 ≤ 0.67·3= 2.01 |
|
0.666 ≤ 0.666… ≤ 0.667 | quindi | 1.998 =0.666·3 ≤ 0.666…·3 ≤ 0.667·3= 2.001 |
|
0.6666 ≤ 0.666… ≤ 0.6667 | quindi | 1.9998 =0.6666·3 ≤ 0.666…·3 ≤ 0.6677·3= 2.0001 |
Operando sulle approssimazioni per difetto mi stabilizzo su 1.999…, su quelle per eccesso su 2.000…. Si tratta di due numeri diversi?
Ecco uno dei problemi che sorge quando si considerano quantità infinite. Noi siamo abituati al fatto che due numeri formati da una
sequenza finita di cifre, a parte gli eventuali "0" iniziali (scrivere 01 al posto di 1), sono uguali solo se hanno le stesse cifre.
Con i numeri formati da infinite cifre questo non vale: 1.999… e 2.000…, pur essendo espressioni diverse, rappresentano lo stesso numero:
sono da intendersi uguali come numeri.
Infatti tra 1.999… e 2.000… non ci sta niente in mezzo: provate a immaginare un numero maggiore di 1.999…
che sia anche minore di 2.000…!
Quindi devono rappresentare lo stesso punto sulla linea dei numeri, o la stessa grandezza fisica, nel caso usassimo i numeri per
rappresentare, ad esempio, un peso o una lunghezza esatta. | 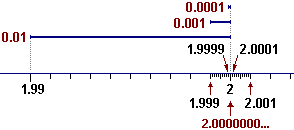 |
Ma si possono, con una misurazione, ottenere misure esatte, infinitamente precise? Esiste un'asta lunga esattamente 2 m, ossia
2.000… m? Ha senso dire che la diagonale di un quadrato di lato 1 m ha diagonale
lunga √2 m, ossia 1.4142135623… m?
Se misuro la lunghezza di un'asta di legno posso trovare che è 27.1 cm. Con un nastro misuratore particolarmente
accurato potrei arrivare a valutare i decimi di millimetro e arrivare alla misura 27.09. Non avrebbe sicuramente senso cercare misure più precise,
in quanto l'asta non è perfettamente liscia.
Considerazioni simili si possono fare per ogni misurazione.
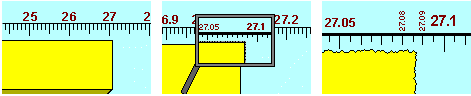
Ma è comodo far finta che esistano misure esatte, è comodo usare i numeri reali (ossia numeri con infinite cifre), ….
Ad esempio è
possibile dire che A = L2 è la formula che esprime l'area di un quadrato in funzione della lunghezza del suo lato,
anche se questa non può essere descritta
esattamente con un numero L, ma solo con un intervallo (ad es. dicendo che sta tra 17.2 e 17.3 cm). Sarà nella applicazione di tale formula che
occorrerà operare con valori approssimati.
Il numero 1.999…, che è uguale a 2, può essere pensato anche come 1 e 9 decimi,
9 centesimi, 9 millesimi, …, ossia come la somma infinita:
| 1 + |
9 | + |
9 | + |
9 | + |
9 | + |
9 | + … |
| — | —— | —— | ——— | ——— |
| 10 | 100 | 1000 | 10000 | 100000 |
[1] Anche le seguenti somme infinite sono numeri? Per rispondere, se ti serve, aiutati con una calcolatrice.
| 3 | + |
3 | + |
3 | + |
3 | + |
3 | + … e così via moltiplicando per 10 il denominatore |
| — | —— | —— | ——— | ——— |
| 10 | 100 | 1000 | 10000 | 100000 |
| 1 + |
1 | + |
1 | + |
1 | + |
1 | + |
1 | + |
1 | + … e così via moltiplicando per 2 il denominatore |
| — | — | — | — | — | — |
| 2 | 4 | 8 | 16 | 32 | 64 |
| 1 | + |
2 | + |
3 | + |
4 | + |
5 | + |
6 | + … e così via aumentando di 1 sia numeratore che denominatore |
| — | — | — | — | — | — |
| 2 | 3 | 4 | 5 | 6 | 7 |
[2] Scova l'errore nella seguente dimostrazione che 1=0.
| (1) So che: | 1 = 1+0 |
(2) So che: | 0 = 0 + 0 + 0 + 0 + … |
(3) So che: | 0 = -1+1 |
(4) Da (2) e (3) ho che: | 0 = (-1+1) + (-1+1) + (-1+1) + (-1+1) + … |
(5) Da (1) e (4) ho che: | 1 = 1 + (-1+1) + (-1+1) + (-1+1) + (-1+1) + … |
(6) Riordino il secondo membro: | 1 = (1-1) + (1-1) + (1-1) + (1-1) + (1-1) + … |
(7) Quindi: | 1 = 0 + 0 + 0 + 0 + … |
(8) Da (2) e (7) ho che: | 1 = 0 |
2. Limiti e ricorsione
Nella scheda 1 (quesito 6) abbiamo visto che se batto su una calcolatrice ad esempio:
5 [√] [√] [√] …
ottengo la successione di uscite:
|
2.23606797749979 | → |
1.495348782057216 | → |
1.222844544494516 | → | ... |
|
1.000012279924602 | → |
1.00000613998115 | → |
... | → | 1 |
Le uscite si stabilizzano su 1. Se facessimo i calcoli esatti, con tutte le cifre invece che con una calcolatrice, che approssima, non arriveremmo
mai a 1, ma a numeri che iniziano con 1.00…0 con una quantità di zero man mano crescente, ossia numeri che tendono a stabilizzarsi su 1.
Per ottenere 1 dovremmo fare infiniti calcoli di radice quadrata. Potremmo scrivere:

ma come capire che i puntini "..." stanno per una quantità infinita di "√"? e come farebbero a starci?
Per risolvere problemi di questo tipo si ricorre a definizioni come le seguenti:
|
|
{ | s(0) = 1
s(n+1) = s(n)+1/2n |
|
La definizione a sinistra corrisponde alla successione di calcoli di radici quadrate appena considerata:
x(0) = 5, x(1) = √x(0) = √5, x(2) = √x(1) = √(√5), x(3) = √x(2) = √(√(√5)), …,
x(n) è il termine che contiene n radici quadrate.
La definizione a destra corrisponde alla seconda somma infinita dell'esercizio 1:
s(0) = 1, s(1) = s(0)+1/2 = 1+1/2, s(2) = s(1)+1/22 = 1+1/2+1/4, s(3) = s(2)+1/23 = 1+1/2+1/4+1/8, …,
s(n) è il termine che che contiene n addizioni.
Per dire che i valori della successione x(0), x(1), x(2), … tendono a stabilizzarsi su 1 si usa scrivere x(n) → 1 per
n → ∞: x(n) tende a 1 per n che tende all'infinito.
Nel caso di s(n), come abbiamo visto nell'esercizio 1 (alla prima addizione mi manca 1/2 ad arrivare a 2,
alla seconda mi manca 1/4 ad arrivare a 2, …), la distanza tra s(n) e 2 tende a 0, ovvero s(n) → 2 per
n → ∞.
[3] Sia q(n) la somma con n addizioni considerata nel terzo caso dell'esercizio 1.
• Completane la definizione seguente:
|
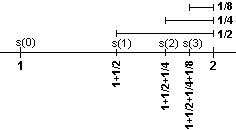 |
q(0) = 1/2, q(n+1) = q(n) + ...
• Come potresti completare la seguente descrizione del suo comportamento per n che tende all'infinito?
q(n) → ... per n → ∞
Un po' di parole.
• Quando, data una successione di valori a(0), a(1), a(2), …, si ha che
a(n) → α per n → ∞ si dice anche che α è il limite
di a(n) (per n che tende all'infinito).
• Definizioni del tipo di quelle date sopra per x(n), s(n) e q(n) vengono chiamate definizioni ricorsive.
Il nome deriva dal fatto che per calcolare un valore,
ad es. x(3), devo ripercorre più volte la definizione, che mi rimanda prima alla determinazione del valore di x(2), poi alla
determinazione di quello di x(1) e, infine, al valore di x(0).
3. Confronti tra insiemi infiniti
Abbiamo visto che, anche se nella pratica non esistono misure per le quali è necessaria un'infinità di cifre per descriverle,
spesso è utile fare questa astrazione [che cosa vuol dire?] e impiegare numeri reali per descrivere grandezze fisiche. Nell'esercizio 7
della scheda 1 abbiamo fatto un'astrazione ben più strana: abbiamo immaginato degli alberghi con infinite stanze. Evidentemente
alberghi di questo genere non esistono e, nella nostra esperienza, non abbiamo mai incontrato neanche altri insieme infiniti di oggetti materiali. Possiamo tuttavia immaginare
insiemi infiniti di "oggetti" inventati dall'uomo: un insieme infinito di parole, un insieme infinito di numeri, ….
L'esercizio era, evidentemente,
un pretesto per una attività di tipo "matematico".
Tuttavia, spesso, nelle applicazioni, è comodo far finta che certe quantità siano
infinite (in fisica, quando si suppone che un corpo sia fatto da infinite particelle "infinitesime", in statistica,
quando si suppone di estrarre un campione da una
popolazione infinita, …).
Ricordiamo che l'esercizio poteva essere risolto in questo modo:
Il Jolly
invece
dello
Star |
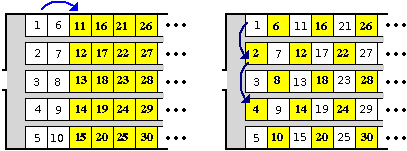 |
Il Jolly
invece
dell'
Eden |
• per liberare 10 posti il proprietario del Jolly fa spostare ogni cliente dalla sua stanza n nella stanza n+10;
• per liberare infiniti posti il proprietario del Jolly fa spostare ogni cliente dalla sua stanza n nella stanza n·2.
Questo esercizio ha messo in luce un paradosso: esistono degli insiemi uno
contenuto strettamente nell'altro che hanno lo stesso numero di elementi, ovvero esiste un insieme che ha degli elementi in più di un altro ma che ha lo stesso numero di elementi.
In realtà le cose non stanno proprio così: gli insiemi dell'esercizio sono infiniti, per cui non possiamo
descriverne la quantità con dei numeri.
|
Infatti un insieme A è finito se è vuoto o se posso "contarlo", ossia, esprimendomi in termini matematici,
se posso trovare una funzione iniettiva che ha esso per dominio e che ha per immagine un "segmento inziale" dell'insieme dei numeri interi positivi,
ossia un insieme del tipo {1, 2, 3, …, n}.
Il numero n è la quantità di elementi di A. Viene chiamato anche cardinalità di A. |
|
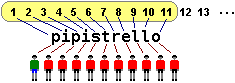
Nel caso
dell'insieme dei caratteri che formano "pipistrello" ho che la sua cardinalità è 11: alla prima "p" associo 1, alla prima "i" associo 2, … alla "o" associo 11;
è una funzione iniettiva in quanto non ho mai associato a due caratteri lo stesso numero. Nel caso dei giocatori di una squadra di calcio, se non so che sono 11, anche senza "contarli" posso stabilire che sono tanti quanti i caratteri di "pipistrello"
associando iniettivamente a ogni giocatore un carattere, e in modo da esaurire tutti i caratteri della parola.
|  |
Generalizzando, nel caso di due insiemi qualunque A e B, anche non finiti,
diremo che hanno la stessa cardinalità se posso
trovare una funzione iniettiva F che ha A come dominio e B come immagine.
Si noti che F ha una funzione inversa G, che ha B come dominio e A come immagine: se F associa ad un elemento a di A l'elemento b di B, G è
la funzione che a b associa a. Nel caso di "pipistrello" e della squadra di calcio, è indifferente se l'associazione la costruisco a partire dai caratteri
della parola o dai giocatori, ossia se, nella figura precedente, i trattini li traccio a partire dalle lettere o a partire dalle figurine dei calciatori. | 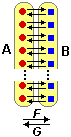 |
Il "paradosso" degli alberghi ci ha portato dunque a concludere che si possono trovare insiemi infiniti della stessa cardinalità contenuti uno strettamente
nell'altro. Invero, questa è una proprietà caratteristica di ogni insieme infinito: posso trovare un suo sottoinsieme proprio (cioè
strettamente contenuto in esso) che ne ha la stessa cardinalità.
Si noti che la strategia adottata dal proprietario del Jolly per evitare quello che ha fatto il proprietario dell'Eden,
ossia:
• portare ogni cliente dalla sua stanza n nella stanza 2n in modo da
liberare le stanze di posto dispari,
possiamo tradurla dicendo che:
• l'insieme dei numeri interi positivi ha la stessa cardinalità del suo sottoinsieme formato dai numeri pari.
Ovviamente, anche il sottinsieme formato dai numeri dispari ha la stessa cardinalità.
[4]
Nella figura immediatamente a destra sono evidenziati due insieme infiniti di punti a coordinate intere: l'insieme A di quelli che stanno sull'asse x,
che formano una specie di semiretta fatta di punti separati, e l'insieme B di quelli che stanno all'interno del 1° quadrante, che formano una
specie di quadrato di dimensioni infinite.
Osservando la figura all'estrema destra, vi sembra che si possa stabilire se A e B hanno o no la stessa cardinalità? Perché?
| 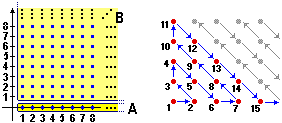 |
Ma vi sono insiemi "più grandi" dell'insieme dei numeri interi positivi?
Sì!
Consideriamo l'intervallo di numeri reali [0,1] (sono i numeri inizianti con "0.", come 0.001…, 0.874…; 1 possiamo pensarlo come 0.999…).
| (1) | Associamo a 1, 2, 3, …, senza ripetizioni, numeri che stanno in [0,1].
Siano x(1) il numero associato a 1, x(2) quello associato ad 2, x(n)
quello associato ad n.
A destra c'è una possibile associazione. |
1 → 0.1422…
2 → 0.6375…
3 → 0.0269…
... ...
|
| (2) | Consideriamo un numero reale y che inizi con "0." e differisca dal primo numero dell'elenco fatto sopra per
la prima cifra frazionaria, che differisca dal secondo per la seconda cifra frazionaria, e così via. Nel caso dell'elenco esemplificato sopra a destra
potremmo prendere, ad es., y = 0.247…. |
y = 0.247… |
| (3) | y sta nell'intervallo [0,1] ma non può comparire nell'elenco in quanto è diverso (per almeno una
cifra) da ciascun numero dell'elenco stesso. |
| (4) | Quindi l'associazione realizzata non può avere come immagine tutto l'intervallo [0,1]. |
In situazioni come questa, tra A = {interi positivi} e B = [0, 1], in cui si può trovare una funzione da A in B che sia iniettiva, ma non se ne
può trovare nessuna che abbia B come immagine, si dice che A è di cardinalità inferiore rispetto a B.
Gli insiemi infiniti che hanno la stessa cardinalità degli interi positivi si dicono infiniti numerabili in quanto possono
essere completamente disposti in un elenco numerato. Dunque, l'intervallo [0,1] è un esempio di infinito non numerabile.
4. Altri paradossi
Gli insiemi infiniti propongono altre situazioni paradossali,
ossia apparentemente assurde.
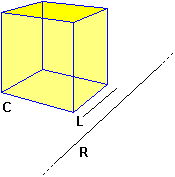
Provate, ad esempio, a mettere in ordine di cardinalità, in base alla vostra intuizione, l'insieme C dei punti che formano un cubo,
l'insieme L dei punti di un suo lato e quello R dei punti che formano una retta.
Vi trovate tutti d'accordo? |
 |
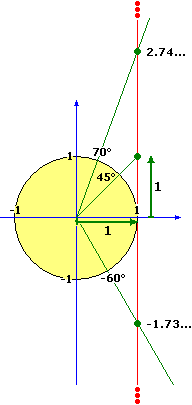 |
[5]
La figura a sinistra illustra come l'intervallo (-90,90) abbia la stessa cardinalità dell'intervallo (-∞, ∞)
• Che cosa rappresenta, secondo te, la funzione che associa gli elementi del primo intervallo a quelli del secondo?
• Hai sciolto qualche dubbio rispetto alla domanda posta all'inizio del paragrafo?
|
Riguarda la figura dell'es. 4. Abbiamo visto che gli elementi
dell'insieme B, che non sono altro che tutte le coppie
(1,1), (1,2), (2,1), (1,3), (2,2), (3,1), … formabili con gli elementi di A = {1, 2, 3, …},
possono essere messi tutte in fila, uno al 1° posto, uno al 2°, e così via.
In questo modo abbiamo visto che
le coppie di numeri interi positivi possono essere associate in modo iniettivo a numeri interi positivi.
Se ci pensi non è una cosa strana. Ad es. le stanze degli alberghi (ancora alberghi!)
e di molti edifici pubblici
non numerate in un modo simile: con 402 si indica la 2ª stanza del 4° piano,
con 713 la 13ª stanza del 7° piano, ….
In pratica le coppie (4,2), (7,13), … vengono
rappresentate ciascuna con un numero intero diverso.
|
Oppure pensa ai numeri di codice impiegati per rappresentare
varie sequenze di informazioni: i codici di prodotti, che racchiudono informazioni
sul tipo di merce, la provenienza, il produttore, …; i codici fiscali delle persone,
che inglobano nome, sesso, data di nascita, …. Sono chiamati "numeri" in quanto, come i
numeri naturali, sono delle sequenze finite di "cifre", realizzate usando come cifre oltre
alle cifre decimali altre lettere dell'alfabeto o altri eventuali simboli (vedi l'es. [3] della scheda A).
[6] I due seguenti esempi illustrano un modo per "codificare"
le terne di numeri reali positivi mediante singoli numeri.
| (513.758…, 23.916…, 3.007…) |
 |
500120333 .790510867… |
= | 500120333.790510867… |
| (1.436…, 673.951…, 100.358…) |
 |
061070133 .493355618… |
= | 61070133.493355618… |
Quali sono (i troncamenti ai centesimi) dei tre numeri reali codificati con 123.456789123…?
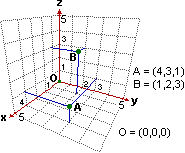 |
Le terne di numeri reali le possiamo usare per rappresentare i punti dello spazio (vedi figura a sinistra).
In particolare il cubo che ha come spigoli gli intervalli [0,1] degli assi x, y e z (vedi figura a destra)
è formato dai punti (a, b, c) con a, b e c
numeri reali tra 0 e 1. Con il procedimento descritto nell'esercizio precedente queste terne di numeri
le possiamo rappresentare con un unico numero compreso tra 0 e 1. |
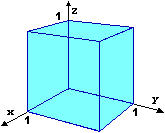 |
Dunque il nostro cubo
ha la stessa cardinalità dell'intervallo [0,1]:
ha tanti punti quanti ne ha un suo lato!
In defintiva, un segmento, una retta, un cubo hanno tutti la stessa cardinalità.
Ha la stessa cardinalità l'intero spazio tridimensionale: le terne di numeri reali sono tante quanti
i numeri reali, ossia tante quante i punti di una retta!
Tutte le figure solide hanno dunque la stessa quantità di punti. Si dice che hanno la cardinalità del continuo. Il termine deriva dal fatto che tutti questi "oggetti" in matematica
e in fisica, quando non si studiano i fenomeni microscopici, si suppone che sia continui, ossia non composti da tante particelle indivisibili. Vi ricordate quanto abbiamo
detto all'inizio della scheda a proposito delle "misure esatte"?
È giusto essere perplessi di fronte a queste conclusioni: una qualunque linea avrebbe tanti punti quanto un qualunque solido! Nella realtà
sappiamo che gli oggetti sono fatti da particelle elementari, che non sono continui, ma per lo studio di molti fenomeni fisici è comodo far finta che
le cose stiano così.
È una supposizione comoda anche in molti altri contesti. Riguardiamo la figura dell'esercizio 5 e ingrandiamone alcuni particolari:
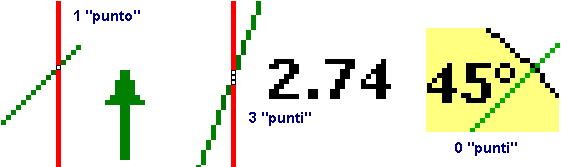
È comodo parlare del punto che si ottiene intersecando una retta con un'altra. Ma questo punto è proprio 1? esiste sempre?
Nel secondo ingrandimento si vede che i "punti", nel disegno fatto al computer, sono tre.
Nel caso illustrato a destra, la
retta scavalca l'arco di cerchio senza avere "punti" in comune con esso.
Se, in matematica o in disegno o in fisica … considerassimo i punti della realtà, ossia
i pixel di un computer, i punti tracciati con una matita, le particelle elementari che formano un oggetto, … invece che i punti della matematica (quelli
che rappresentiamo con coordinate usando i numeri reali) sarebbe assai più complicato parlare in modo comprensibile.
5. Concludendo ...
Questo piccolo percorso sull'infinitamente grande e l'infinitamente piccolo ci dovrebbe aiutare a capire come
i modelli astratti, di cui è piena la matematica,
non sono stati inventati per renderci le cose più difficili, bensì più semplici.
Ci dovrebbe, tuttavia, anche far pensare al fatto che, quando si usa la matematica, si deve tener conto delle astrazioni operate, per non trarre conclusioni errate
o per tener conto
della natura approssimata di esse, nel momento in cui dobbiamo applicarle nella pratica.
 | Per esempio, nel riflettere sul paradosso della luce
che entra nello specchio a spirale, presentato alla fine della scheda 1, occorre tener presente che si tratta di un "gioco matematico":
•
è vero che lo spazio totale che dovrebbe percorrere la luce è finito: abbiamo visto che (1+1/2+1/4+1/8+…) m = 2 m; la luce impiegherebbe
un attimo ad uscire dalla spirale;
• ma il fatto che non si possa determinare la direzione
con cui uscirebbe in quanto non esiste un ultimo specchio su cui la
luce rimbalza è frutto dell'astrazione di supporre che gli specchi siano delle superfici piane senza spessore (altrimenti non
potrebbero formare una spirale senza fine). |
|
In altre parole, abbiamo usato il modello astratto oltre i suoi realistici ambiti di applicazione.
|
Con i tuoi insegnanti, e con tue eventuali ricerche, letture e riflessioni
personali
o in eventuali studi futuri, potrai approfondire queste tematiche, e vedere come
si intrecciano, forse per te inaspettatamente, a molti contesti
(arte pittorica, musica, informatica, linguistica, …). Buon viaggio.
L'infinitamente grande e l'infinitamente piccolo
Attività varie
Si tratta di esercizi (o proposte/spunti per attività più complesse) articolabili in vario modo (a seconda del tipo
di classe, dell'impiego in aula normale o in aula computer, …).
[ ] In una data calcolatrice il tasto  azzera la memoria,
azzera la memoria,  addiziona al numero in memoria il numero che appare sul visiore,
addiziona al numero in memoria il numero che appare sul visiore,  ricopia sul visore il numero che è in memoria,
ricopia sul visore il numero che è in memoria,  esegue i calcoli impostati e visualizza il risultato.
Batti:
esegue i calcoli impostati e visualizza il risultato.
Batti:
Proseguendo, che cosa ottieni? E se batti 4 invece di 9? e se battessi 2?
Provate a descrivere con un diagramma di flusso o con una definizione ricorsiva o in qualche altro modo il procedimento di calcolo che avete eseguito.
alternativa (ma, volendo, è integrabile alla precedente)
[ ] Sia A = 4. Considera la successione di valori x(0), x(1), x(2), … così definita:
| { |
x(0) = 1
x(n+1) = (x(n)+A/x(n))/2 |
|
-
Utilizzando un foglio di calcolo studiane il comportamento per n → ∞.
- Come sopra, con A = 4 e con A = 2.
|
[ ] Prova ad aprire questi due file:
algoritmo 1,
algoritmo 2
e
algoritmo 3.
• Come descriveresti ciò che realizzano.
• Analizza il codice sorgente di questi file. Cerca di capire, informandoti sugli script,
come sono stati realizzati, e cerca di realizzare file analoghi per mettere in corrispondenza i numeri interi
positivi con i numeri dispari positivi, per generare la successione sotto descritta ricorsivamente (con il
valore di A inseribile da parte dell'utente)
ed altre successioni definite ricorsivamente a tuo piacere.
| { |
x(0) = 1
x(n+1) = (x(n)+A/x(n))/2 |
[ ] Realizza, mediante un foglio di calcolo o un linguaggio di programmazione,
un algoritmo che generi potenzialmente tutte le cifre del risultato della divisione tra M e N numeri interi con 0 < M < N.
Come lo puoi modificare in modo da ottenere il risultato in base 2?
[ ] Realizza, mediante un foglio di calcolo o un linguaggio di programmazione,
un algoritmo che generi la successione x(0), x(1), x(2), …, dove x(n) = 2x con x approssimazione per troncamento
di π alla cifra che rappresenta le potenze di 10 alla -n.
[ ] Esiste un numero reale positivo che sia inferiore
a tutti gli altri numeri positivi? E, tra i numeri positivi della tua calcolatrice, ce n'è inferiore a tutti gli altri? E ce n'è uno che sia maggiore di tutti gli altri.
[ ] Abbiamo visto che tra due numeri reali qualunque ce ne sono infiniti altri:
basta che faccia la media tra di essi per trovarne uno, poi la media tra questo nuovo numero e uno dei precedenti, e così via.
Ma se con una calcolatrice a 8 cifre eseguo (8.7654321+8.87654322)/2 e ottengo 8.87654320 che non sta in mezzo ai due numeri. Come è
possibile?
[ ] Considera un foglio di calcolo elettronico così impostato:
| | A | B |
| 1 | =2000.07-2000.03 | =IF(A1=0.04;1;0) |
["=IF(test;P;Q)" si comporta come "IF test THEN PRINT P ELSE PRINT Q"; in alcuni fogli di calcolo, a seconda delle opzioni scelte, viene usato "SE" al posto di "IF"]
• Se si visualizzano i valori, che cosa ti aspetti di ottenere?
• Verifica la tua ipotesi.
• Prova a completare la seconda riga nel modo seguente e visualizzane i valori dando alla cella A2 l'opzione di rappresentare i numeri con 20 cifre.
Che cosa ottieni?
| | A | B |
| 1 | =2000.07-2000.03 | =IF(A1=0.04;1;0) |
| 2 | =2000.07-2000.03 | =(A1-0.04)*10^50 |
• Cerca di spiegare il fenomeno osservato.
[ ] Osserva il grafico della funzione arctan. Tale funzione può
essere usata per esprime il fatto che due insiemi hanno la stessa cardinalità. Quali?
[ ] Congiungo due punti con un semicerchio. La distanza tra i punti è 1 e quindi il semicerchio è lungo π.
Poi congiungo i due punti sostituendo il semicerchio con due semicerchi di diametro 1/2.
Poi sostituisco ciascuno di questi semicerchi con due di diametro 1/4. E così via, come illustrato sotto.
• Si modifica la lunghezza del percorso al cambiare della forma? Procedendo
all'infinito, che forma tende ad assumere il percorso? Quanto è lunga questa figura limite?
• Sintetizza quanto osservato indicando Fig(n) la figura formata da n semicerchi, con F la figura limite, con Lun(C) la lunghezza
di una generica curva C.
Per n → ∞ Fig(n) → ... per n → ∞ Lun(Fig(n)) → ...
mentre Lun(F) =
[ ] Le immagini di un film sono dinamniche, vediamo i movimenti con continuità. Come è possibile che siano
realizzate con un insime finito di fotogrammi? Approfondisci l'argomento dal punto di vista "tecnico" e "psicologico".
Riesci a individuare qualche collegamento col "paradosso della freccia" di Zenone? (informati su questo
paradosso, se non lo conosci)
[ ] Ho una moneta non truccata e la lancio ripetutamente.
• Qual è la probabilità che esca testa al 1° lancio?
• Qual è la probabilità che la prima testa esca al 2° lancio?
• Qual è la probabilità che la prima testa esca al 3° lancio?
• Qual è la probabilità che la prima testa esca all'n° lancio?
• Quale o quali tra le seguenti espressioni rappresentano la probabilità che prima o poi esca testa? Perché?
(1) 50%
(2) 100%
(3) 1/2 + 1/4 + 1/8 + 1/24 + 1/25 + …
(4) il limite per n → ∞ di p(n) dove p(1) = 1/2, p(n+1) = p(n)+1/2n
[ ] Lancio un aereoplanino di carta dalla Torre Eiffel.
E' più probabile che tocchi terra esattamente dopo √2 minuti o esattamente dopo 10π minuti?
Quanti sono gli istanti possibili in cui può toccare terra?
[ ] Realizza, mediante un foglio di calcolo o un linguaggio di programmazione,
un algoritmo che simuli il lancio di due dadi, generando le uscite di successivi lanci e, via via, la frequenza con cui esce
7. Fai delle congetture sull'eventuale valore su cui tende a stabilizzarsi questa frequenza e cerca di discuterle con
qualche considerazione teorica?
[ ]
Se proseguono così vediamo Mario e Luigi incontrarsi.
Ma si incontrano? | 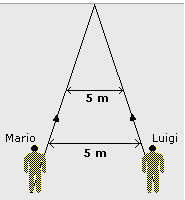 |
[ ] Realizza, mediante un foglio di calcolo o un linguaggio di programmazione,
un algoritmo che, data una funzione F e un intervallo [a,b] contenuto nel suo dominio, permetta di calcolare (quando sia possibile)
la lunghezza del grafico di F in [a,b]
mediante la generazione delle lunghezze di poligonali con vertici sul grafico ottenute inserendo via nuovi vertici tra i vecchi.
Sperimenta, poi, l'algoritmo su diverse funzioni.
Un programma per generare/visualizzare frattali
(vedi l'articolo su Matematica e Computer di L.Repetto).
Altri possibili sviluppi e spunti sono ricavabili dagli Oggetti Matematici:
lunghezza
aree
immagini digitali
limiti
prospettiva
i "numeri macchina"
Achille e la tartaruga e altro
altre voci (pendenza2, velocità, ..., infiniti e infinitesimi)
Spunti per ricerche in Internet (possibili sequenze di parole chiave):
somma infinita
infinito infinitesimo storia
infinitesimo continuità
continuità punto intersezione
supertask paradox
loop paradosso
informatica infinito
ricorsione infinito
pittura punti infinito
infinito arte grafica
infinito linguistica generare
letteratura infinito
tristram shandy russell
paradox benardete



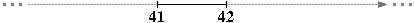







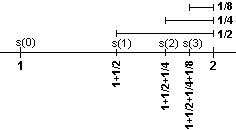









 azzera la memoria,
azzera la memoria,  addiziona al numero in memoria il numero che appare sul visiore,
addiziona al numero in memoria il numero che appare sul visiore,  ricopia sul visore il numero che è in memoria,
ricopia sul visore il numero che è in memoria,  esegue i calcoli impostati e visualizza il risultato.
Batti:
esegue i calcoli impostati e visualizza il risultato.
Batti: