Dal grafico della  velocità (in m/s) v in funzione del tempo (in s) t come posso risalire al grafico della strada percorsa (in m) s in funzione di t ?

    Intuisco che il grafico di s sia corretto;  v non è altro che la derivata s' di s e il grafico di v sembra rappresentare come varia la pendenza lungo il grafico di s:  inizialmente questo ha pendenza costante (30/3 = 10),  poi sale con la concavità verso l'alto, ossia con pendenza via via crescente,  fino a t=5, in cui la pendenza inizia a diminuire,  fino ad arrivare a t=10, in cui la pendenza diventa nulla.
    Si intuisce pure che il grafico di s in funzione di t rappresenta anche come varia l'area A delimitata (nel modo illustrato sotto a sinistra) dal grafico di v (ovvero di s').  Sotto a destra puoi accedere ad una animazione che illustra meglio il fenomeno.

(vedi un'animazione con R)
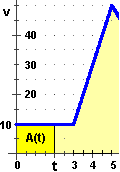
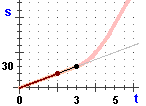
Precisiamo questa intuizione.     Nel tratto iniziale, da t=0 a t=3, in cui v è costante, s varia proporzionalmente a t :  s = 10 t.     In pratica, s è rappresentata dall'area A(t) del rettangolo di altezza v e base t.     Arrivati a t = 3, la strada percorsa è 3·10 = 30, pari all'area del rettangolo di base 3 e altezza.          Tra t=3 e t=5 v(t), ossia s'(t), non è costante, ma posso stimare lo spazio percorso per piccoli Δt supponendo che ivi v sia costante, ossia che s ivi vari proporzionalmente a t.     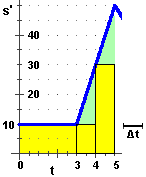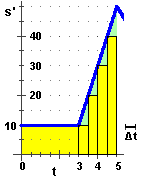A sinistra è illustrato che cosa accade se prendo Δt = 1. Tra t=3 e t=4 per v=10 percorrerei la strada 1·10, che corrisponde all'area del primo rettangolino; tra t=4 e t=5 per v=30 percorrerei la strada 1·30, che corrisponde all'area del secondo rettangolino.     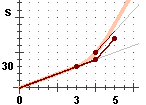Il grafico di s tracciato a destra è stato ottenuto in questo modo: • da (3,30) si passa a (4,30+10) = (4,40); si è proceduto come se la pendenza si mantenesse uguale a 10; • poi si passa a (5,40+30) = (5,70); si è proceduto come se la pendenza si mantenesse uguale a 30.     Avrei potuto tracciare il grafico direttamente: • tra 3 e 4 suppongo che s(t) vari con la stessa velocità s' che aveva in 3 (ossia approssimo s con la funzione lineare che ha s'(3)=10 come pendenza); • tra 4 e 5 suppongo che s(t) vari con la stessa velocità che aveva in 4 (ossia approssimo s con la funzione lineare che ha s'(4)=30 come pendenza).         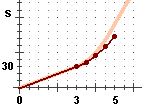A destra è illustrato che cosa accade se prendo Δt = 0.5.     In breve, dall'istante t all'istante t+Δt, s(t) varia di circa s'(t)Δt (si veda il concetto di  differenziale), e questo valore rappresenta anche l'area del rettangolino di base Δt e altezza s'(t) che approssima l'incremento dell'area A(t). Quanto più piccolo è Δt tanto migliori sono queste approssimazioni.     In altre parole, ΔA(t) approssima s'(t)Δt, ossia ΔA(t)/Δt approssima s'(t), e questa approssimazione migliora quanto voglio a patto che prenda Δt sufficientemente piccolo, ossia, per Δt → 0, otteniamo A'(t) = s'(t).       Questo procedimento chiarisce, dunque, l'intuizione iniziale: trovare il grafico di s in funzione di t a partire dal grafico di s' in funzione di t equivale a tracciare il grafico dell'area A(t) tra grafico di s' e asse orizzontale che è compresa tra le rette verticali di ascissa 0 e di ascissa t.