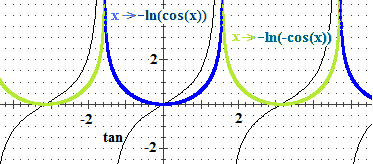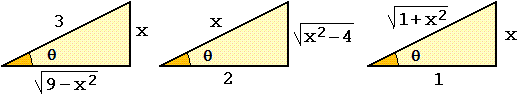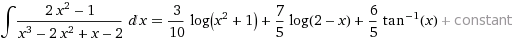Calcolo degli integrali

  Alla voce  integrale abbiamo visto se f è una funzione continua in [a, b] o è ivi limitata e discontinua in al più un numero finito di punti, allora esiste ∫_{[a, b]} f  (abbiamo anche richiamato, qui, la possibilità di usare metodi di calcolo approssimato per calcolare gli integrali in un dato intervallo).
    Se inoltre f è periodica abbiamo visto che, se T è il periodo ed I e J sono due intervalli ampi T, allora  ∫ _I f = ∫ _J f.
    Si è poi visto che se f e g sono integrabili su [a, b] allora  ∫_{[a, b]} f + g = ∫_{[a, b]} f + ∫_{[a, b]} g  e  ∫_{[a, b]} f − g = ∫_{[a, b]} f − ∫_{[a, b]} g,  e che se k è un numero qualunque  ∫_{[a, b]} k f = k ∫_{[a, b]} f .
    Abbiamo, poi, posto  ∫_{[b, a]} f = − ∫_{[a, b]} f,  e abbiamo visto che, se f è integrabile tra a e b, tra b e c, e tra a e c,  ∫ _{[a, b]} f + ∫ _{[b, c]} f = ∫ _{[a, c]} f
    Infine abbiamo considerato la formula fondamentale del calcolo integrale:

se f è continua in [a, b] e  G' = f  allora  ∫ _{[a, b]} f = G(b) − G(a).

∫ _{[1, 3]} 1/t dt = ?   D_x log(x) = 1/x;   ∫ _{[1, 3]} 1/t dt = [log(x)]_x=3 − [log(x)]_x=1 = log(3) − log(1) = log(3).

    Abbiamo, infine, introdotto    ∫ f(x) dx  per indicare un generico termine g(x) tale che g'(x) = f(x);  l'operazione che ad f(x) associa tale termine viene chiamata integrazione indefinita, mentre l'aggettivo definita viene riservato all'associazione alla funzione e ad un intervallo [a, b] del numero ∫ _{[a, b]} f.
    Qualche volta scriviamo  ∫ f(x) dx = g(x) e qualche altra volta  ∫ f(x) dx = g(x) + c,  per esplicitare che tutti i termini g(x) + c, al variare di c in IR, hanno per derivata (rispetto ad x) f(x)  (ricordiamo che in qualche caso si usano "+ c₁", "+ c₂", … per intervalli diversi).

    Ad esempio per trovare  ∫ (e^x + x⁻² + x + 3) dx  cerco f tale che df / dx = e^x + x⁻² + x + 3.  Quindi va bene  f(x) = e^x − x⁻¹ + x²/2 + 3x  e, più in generale,  f(x) = e^x − x⁻¹ + x²/2 + 3x + c  al variare di c in IR.

    Abbiamo, infine, visto che, mentre se integro una funzione polinomiale ottengo ancora una funzione polinomiale  ( ad es. se F(x) = 3x²+x−3√2  ho che  ∫ F(x) dx = x³+x²/2−3√2x+c, al variare di c in IR ),  in generale, di fronte a una cosiddetta funzione elementare  (ottenibile mediante successive composizioni di funzioni polinomiali, di elevamento a potenza, esponenziali, logaritmiche, circolari e circolari inverse)  non siamo sempre in grado di esprimerne mediante una formula analoga la funzione integrale.  Ad es. di fronte a F(x) = e^x2 so che F'(x) = 2x e^x2 ma non riesco a trovare alcuna funzione elementare la cui derivata sia F(x).
    In questa voce vedremo alcuni "trucchi", alcuni più significativi altri meno (e, comunque, ormai incorporati in vari tipi di software), per trovare, in molti casi, l'integrale di una funzione data.

  Integrazione per parti

Questo "trucco" si basa su una riscrittura della regola della derivazione del prodotto (  propr. f. cont. e derivabili):
D(f·g) = D(f)·g + g·D(f)  →  g·D(f) = D(f·g) − D(f)·g  →  ∫g·D(f) = f·g − ∫D(f)·g
    Un esempio:

∫ x e^x dx   Idea: è il prodotto di due termini, x ed e^x, dei quali il primo ha una derivata più semplice [D_x(x) = 1]  e il secondo può essere interpretato facilmente come la derivata di un altro termine [e^x = D_x(e^x) = e^x]. Quindi:
∫ x e^x dx = ∫ x D_x(e^x) dx = x e^x − ∫ D_x(x) e^x dx = x e^x − ∫ e^x dx = x e^x − e^x (+ c)

(in modo simile posso ricondurre  ∫ x³ e^x dx  a  x³ e^x − 3 ∫ x² e^x dx,  e così via) 

    A volte è utile il trucco di immaginare la presenza di un fattore "·1" da interpretare come D(f):
∫ log(x) dx = ∫ 1·log(x) dx = ∫ D_x(x)·log(x) dx = x·log(x) − ∫ x·D_x(log(x)) dx = x·log(x) − ∫1 dx = x·log(x) − x  (+ c)

    Altre volte è utile il trucco di usare l'integrazione per parti per esprimere l'integrale in funzione di sé stesso, e quindi risolvere l'equazione ottenuta:
∫ log(x)/x dx = ∫ 1/x·log(x) dx = ∫ D_x(log(x))·log(x) dx = log(x)·log(x) − ∫ log(x)/x dx
da cui  2 ∫ log(x)/x = log(x)², e quindi  ∫ log(x)/x dx = log(x)²/2

    In alcuni casi è necessario intergrare per parti più volte:
∫ e^xcos(x) dx = ∫ D_x(e^x) cos(x) dx = e^xcos(x) − ∫ e^xsin(x) dx
In modo analogo   ∫ e^xsin(x) dx = ∫ D_x(e^x) sin(x) dx = e^xsin(x) − ∫ e^xcos(x) dx
Quindi   2 ∫ e^xcos(x) dx = e^xcos(x) + e^xsin(x) (+ c)   da cui  ∫ e^xcos(x) dx = e^x (cos(x) + sin(x)) / 2 (+ c)
( verifica: D_x (e^x (cos(x)+sin(x))/2) = ... = e^x cos(x) )

    Ecco un esempio di integrazione per parti di un integrale definito:
∫ _{[0, 1]} arctan(x) dx   Osserviamo, innanzi tutto, che la funzione integranda è definita e continua su tutto IR e, quindi, su [0, 1]. Quindi ha senso l'esercizio. Troviamo, prima, l'integrale indefinito. Procedendo per parti:  ∫ arctan(x) dx = ∫ D_x(x) arctan(x) dx = x·arctan(x) − ∫ x·1/(1+x²) dx = #   Ricordo che:   D(log(f(.)) = 1/f · D(f).  Quindi:   # = x·arctan(x) − log(1+x²)/2.  Infine:   ∫ _{[0, 1]} arctan(x) dx = [x·arctan(x)] _x=0..1 − [log(1+x²)/2] _x=0..1 = π/4 − log(2) / 2.

    I calcoli/le verifiche con R.

Esercizi:   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione

  Integrazione per sostituzione

Questo è il più importante metodo di integrazione. Esso si basa sulla regola della derivazione delle funzioni composte. Partiamo da due esempi abbastanza semplici.

• ∫ 2x(x²−1)⁴ dx  posso interpretarlo come  ∫ g'(x) g(x)⁴ dx  con g(x) = x²−1.  So che  ∫ x⁴ dx = x⁵/5  (+ C).
Posso concludere che  ∫ 2x(x²−1)⁴ dx = g(x)⁵/5 = (x²−1)⁵/5  (+ C)
[  Controllo con R: f=function(x) (x^2-1)^5/5; D(body(f),"x") o con WolframAlpha: integral 2*x*(x^2-1)^4 dx ]

• ∫ tan(x) dx  posso interpretarlo come  ∫ sin(x)/cos(x) dx = ∫ −g'(x)·1/g(x) dx  con g(x) = cos(x).  So che ()  ∫ 1/x dx = log(x) (+ C₁)  o che  ∫ 1/x dx = log(−x) (+ C₂).
Posso concludere che  ∫ tan(x) dx = −log(cos(x)) (+ C₁)  o  ∫ tan(x) dx = −log(−cos(x)) (+ C₂)

Le soluzioni corrispondenti a Ci = 0

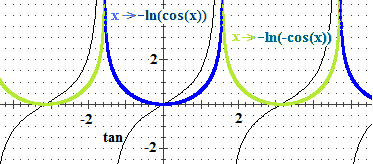(Ho infinite diverse costanti C_i per ciascun intervallo che forma di dominio)

    In generale,  ∫ f(g(x)) g'(x) dx  si affronta ponendo  u = g(x),  du = g'(x) dx,  risolvendo  ∫ f(u) du  e risostituendo  g(x)  ad  u.

    Rivediamo gli esempi precedenti.
∫ 2x(x²−1)⁴ dx,   u = x²−1,  du = 2x dx,  ∫ u⁴ du = u⁵/5,   ∫ 2x(x²−1)⁴ dx = (x²−1)⁵/5 (+ C)
∫ sin(x)/cos(x) dx,   u = cos(x),  du = −sin(x) dx,  ∫ −1/u du = −∫ 1/u du = −log(u)  o  ∫ −1/u du = −log(−u),   ∫ sin(x)/cos(x) dx = −log(cos(x)) (+ C₁)  o  ∫ sin(x)/cos(x) dx = −log(−cos(x)) (+ C₂).

    Altro esempio:  ∫ 1 / (4x−3)² dx
Pongo  u = 4x−3.  du = 4 dx,  dx = 1/4 du,  1/4·∫ 1/u² du = −1/(4u).  Quindi  ∫ 1 / (4x−3)² dx = −1/(4(4x−3)).  Ovvero:  ∫ 1 / (4x−3)² dx = −1/(4(4x−3)) + C₁ per x < 3/4,  ∫ 1 / (4x−3)² dx = −1/(4(4x−3)) + C₂ per x > 3/4.

    Ulteriore esempio:  ∫ x √(x−3) dx
In questo caso non è evidente se procedendo per sostituzione si riesce a calcolare l'integrale. Proviamo.
Pongo  u = x−3.  du = dx,  x = u+3.  ∫ (u+3)√u du = ∫ u^3/2+3u^1/2 du = 2/5 u^5/2 + 2 u^3/2  Quindi:  ∫ x √(x−3) dx = 2/5 (x−3)^5/2 + 2 (x−3)^3/2 (+ C).

    Vediamo un altro esempio:   ∫ (1+e^x)/(1−e^x) dx
La presenza preponderante di e^x mi suggerisce la sostituzione u = e^x, ossia x = log(u).
dx = 1/u du;   allora ottengo:   ∫(1+u)/(1-u) 1/u du
A questo punto cerco di sbarazzarmi del rapporto tra polinomi di grado 1:
(1+u)/(1−u) 1/u = (1−u+u+u)/(1−u) 1/u = (1 + 2u/(1−u)) 1/u = 1/u + 2/(1−u)
∫(1+u)/(1−u) 1/u du = log(u) − 2 log(1−u)
∫(1+e^x)/(1−e^x) dx = log(e^x) − 2 log(1−e^x) = x − 2 log(1−e^x)  (+c)
    Se provassi a fare il calcolo con WolframAlpha otterrei lo stesso risultato ma con altri programmi di calcolo simbolico(come Maple) potrei otterrere:
integral (1+exp(x))/(1-exp(x)) dx = x − 2 log(e^x−1)  (+c).     Chi ha ragione?  Facciamo il grafico dell'integranda (blu) e delle due funzioni soluzione (con c=0) e cerchiamo di capire:

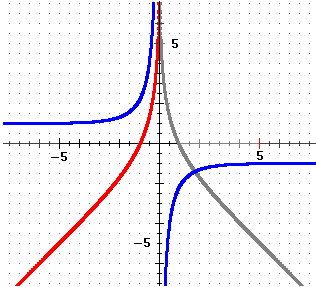Entrambe le funzioni (quella in rosso - e quelle ottenibili con sue traslazioni verticali - e quella in grigio - e quelle ottenibili con traslazioni verticali) sono soluzioni del nostro integrale: una lo è a sinistra di 0, l'altra a destra.  Sia il procedimento "manuale" che quello al computer hanno trascurato dei casi.  Il tracciamento del grafico della funzione e delle soluzioni (o l'immaginarli) ci è di aiuto per capire la situazione, e che le soluzioni sono: x − 2 log(1−ex)  (+c1)     x − 2 log(ex−1)  (+c2)     Questo è un problema tipico in cui affidandosi al solo calcolo è facile commettere errori (qui l'errore è stato non tener conto che ∫ 1/x dx è, a meno di costanti additive, log(|x|), non log(x), come si è già visto all'inizio del paragrafo).

Ecco un esempio di integrazione per sostituzione di un integrale definito:

∫ _{[0, 2]} x e^x2dx   Prima calcoliamo l'integrale indefinito. Poniamo u = x².  du = 2x dx.  ∫ e^u/2 du = e^u/2.  Quindi:  ∫ x e^x2dx = e^x2/ 2 (+ C).  Infine:  ∫ _{[0, 2]} x e^x2dx = [e^x2/ 2]_x=2 − [e^x2/ 2]_x=0 = (e⁴−1)/2.  Posto u = x², potevo procedere anche nel modo seguente.
∫ _{[0, 2]} x e^x2dx = ∫ _{[0, 4]} e^u/ 2 du  in quanto, per x che varia tra 0 e 2, u = x² varia tra 0 e 4.
Questo secondo metodo funziona quando du/dx (2x in questo caso) è funzione continua di x. Per un semplice controesempio si pensi a ∫ _[−1,1] |x| dx, che vale evidentemente 1 (è l'area di mezzo quadrato di diagonale 2). Con la sostituzione u = |x| mi ricondurrei ad un integrale tra 1 ed 1, che vale 0.

    Ricordiamo, infine, che se l'integranda è una funzione razionale di sin e/o di cos può essere comoda la sostituzione  t = tan(x/2):

∫ 1/(2+cos(x)) dx = (*)     t = tan(x/2),  cos(x) = (1−t²)/(1+t²),  dx = 2dt/(1+t²)
∫ 2dt/(1+t²) / ((3+t²)/(1+t²)) = 2 ∫ 1/(3+t²) dt = 2/√3 atan(t/√3)    (*) = 2/√3 atan(tan(x/2)/√3)

f(x) = 1/(2+cos(x)) g(x) = 2/√3 atan(tan(x/2)/√3)

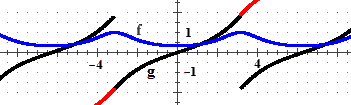Occorre, però, stare attenti al dominio (come anche in altri casi di integrazione). Nel nostro caso la soluzione proposta non è definita su tutto IR, come lo è invece la funzione intergranda. Ad esempio la soluzione che in 0 vale 0  coincide in (−π, π) con la funzione g rappresentata graficamente sopra. Ma per x → π−  g(x) → π/√3; analogamente per x → −π+  g(x) → −π/√3. Posso estendere g ad una soluzione definita su tutto IR ponendo g(π) = π/√3, g(−π) = −π/√3 e poi prolungandola per continuità ad una funzione G nel modo sopra raffigurato in rosso, ossia traslando verticalmente g in modo opportuno negli altri intervalli; ad es. per x in (π, 2π) prendendo G(x) = g(x)+2π/√3.  Le altre soluzioni sono  G(x) + C  al variare di C in IR.  Sarebbe, quindi, sbagliato scrivere che le soluzioni sono 2/√3 atan(tan(x/2)/√3) + C.

Esercizi:   testo  e  sol.,   testo  e  sol.,   testo  e  sol.,   testo  e  sol.,   testo  e  sol.,   testo  e  sol.,   testo  e  sol.,   testo  e  sol.

  Integrazione per sostituzione trigonometrica

Esisitono alcuni "trucchi" per calcolare con sostituzione alcuni tipi particolari di integrali, in cui si utilizzano le relazioni tra gli elementi di un triangolo rettangolo (tuttavia, anche in questi casi, esiste del software che esegue automaticamente i calcoli).  Facciamo degli esempi, riferendoci alle figure seguenti (che valgono solo per x e θ positivi, ma suggeriscono relazioni che possono valere anche per x e θ negativi).

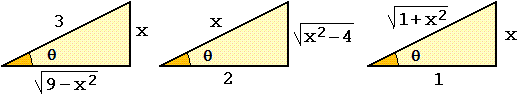
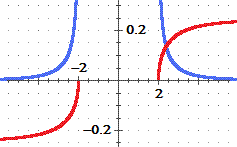
∫ 1/√(9−x2) dx     può essere affrontato (vedi figura a sinistra) pensando a  √(9−x2) = 3·cos(θ),  x = 3·sin(θ),  dx = 3·cos(θ) dθ ∫ 3·cos(θ) / (3·cos(θ)) dθ = ∫ 1 dθ = θ ∫ 1/√(9−x2) dx = asin(x/3)  (+c)   (a destra il controllo "grafico") [con WolframAlpha vasta battere: integral 1/sqrt(9-x^2) dx]		x → 1/√(9−x2) x → asin(x/3)
∫ 1 / ( √(x2−4) x2 ) dx     può essere affrontato (vedi figura sopra al centro) pensando a  √(x2−4) = 2·tan(θ),  2/x = cos(θ), da cui  x = 2/cos(θ), dx = 2·tan(θ)/cos(θ) dθ.

Quindi  ∫ 1 / (2·tan(θ)·4/cos(θ)2)·2·tan(θ)/cos(θ) dθ = ∫ 1/4 cos(θ) dθ = sin(θ)/4 (+c) ∫ 1 / ( √(x2−4) x2 ) dx = √(x2−4) / (4x) (+c)   (a sinistra il controllo "grafico") x → 1 / ( √(x2−4) x2 )    x → √(x2−4) / (4x)

∫ _{[−1, 1]} 1 / (1+x²)² dx   è un integrale definito che possiamo affrontare considerando il triangolo rettangolo raffigurato sopra a destra:
x = tan(θ),  1/√(1+x²) = cos(θ),  dx = 1/cos(θ)² dθ.  Per x che varia tra −1 e 1  θ varia tra −π/4 e π/4.
∫ _{[−1, 1]} 1 / (1+x²)² dx = ∫ _{[−π/4, π/4]} cos(θ)⁴ / cos(θ)² dθ = ∫ _{[−π/4, π/4]} cos(θ)² dθ = ∫ _{[−π/4, π/4]} (1−cos(2θ))/2 dθ = [(θ+sin(2θ)/2)/2] _{θ = −π/4 .. π/4} = π/4 + 1/2.

[con R: f=function(x) 1/(1+x^2)^2; integra(f,-1,1); pi/4+1/2
# 1.285398  1.285398]

Esercizio:     testo  e  soluzione

  Integrazione di funzioni razionali

Illustriamo i procedimenti che si possono impiegare per integrare le cosiddette funzioni razionali, ossia le funzioni esprimibili come rapporto tra funzioni polinomiali, attraverso alcuni esempi.

∫   3x3−2x2−19x−7  dx ——————— x2−x−6

Innanzi tutto trasformo il rapporto eseguendo la divisione in modo di ricondurmi ad un rapporto in cui il primo termine abbia grado minore:

3 2 2 3 x - 2 x - 19 x - 7 | x - x - 6 ----------- 3 2 3 2 | 3 x [ <-- 3x / x ] 3 x - 3 x - 18 x | -------------------- | 2 | 2 2 x - x - 7 | 1 [ <-- x / x ] 2 | x - x - 6 | ------------- | - 1

∫ (3x³−2x²−19x−7) / (x²−x−6) dx = ∫ 3x+1 + (−1) / (x²−x−6) dx = ∫ 3x+1 dx − ∫ 1 / (x²−x−6) dx.
Il primo integrale so che fa  3x²/2+x (+c).
x²−x−6  posso scomporlo in (x+2)(x−3), per cui posso dedurre che  1 / (x²−x−6)  può essere scomposto additivamente come  A/(x+2) + B/(x−3).  Eguagliando i due termini trovo  1 = A(x−3) + B(x+2), ovvero  1 = (A+B)x + 2B−3A,  da cui A = −B, B = 1/5.
Quindi  ∫ 1 / (x²−x−6) dx = ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx. Il dominio è costituito dall'unione degli intervalli (−∞, −2), (−2, 3), (3, ∞). Nel primo intervallo  ()  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(−x−2)/5 + log(3−x)/5 (+ c1), nel secondo  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(x+2)/5 + log(3−x)/5 (+ c2), nel terzo  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(x+2)/5 + log(x−3)/5 (+ c3).

Perciò l'integrale della funzione iniziale è  3x2/2+x+log(−x−2)/5−log(3−x)/5 (+c1) per x in (−∞,−2), 3x2/2+x+log(x+2)/5−log(3−x)/5 (+c2) per x in (−2,3), 3x2/2+x+log(x+2)/5−log(x−3)/5 (+c3) per x in (3,∞).
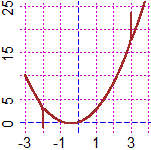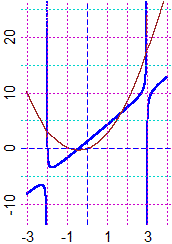
	Potremmo esprimere l'integrale come  3x2/2+x+log(|x+2|)/5−log(|x−3|)/5, ovvero come  3x2/2 + x + log(|(x+2)/(x−3)|) / 5  in ognuno dei tre intervalli, in ciascuno dei quali si possono aggiungere diverse costanti.  A destra in rosso è raffigurata la funzione da integrare e, in colori scuri, i grafici dei tre rami di curva che, a meno di innalzamenti o abbassamenti, ne rappresentano l'integrale.  Questi sono ripresi a sinistra, evidenziandone meglio l'andamento per x che tende a −2 e a 3. [verifica con R]

∫   x − 1  dx —————— x2 (x2 + x + 1)

Consideriamo l'integrale a sinistra.

x²+x+1 è irriducibile. Cerco di riscrivere l'integranda così:

x − 1	=	A	+	B	+	Cx+D	Ho:  x−1 = Ax(x2+x+1)+B(x2+x+1)+(Cx+D)x2
——————		—		—		————
x2 (x2 + x + 1)		x		x2		x2+x+1

Raccogliendo i termini ottengo A+C = 0, A+B+D = 0, A+B = 1, B = −1,  da cui: A = 2, B = −1, C = −2, D = −1.  Quindi ho ricondotto l'integrale di partenza a  ∫ 2/x − 1/x² − (2x+1)/(x²+x+1) dx.

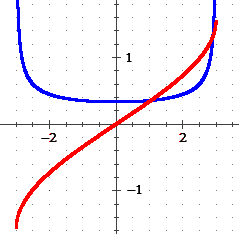
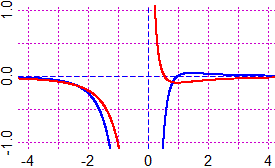
•  ∫ 2/x dx = 2·log(|x|), ovvero ∫ 2/x dx = 2·log(x) + C1 per x > 0, ∫ 2/x dx = 2·log(−x) + C2 per x < 0. •  ∫ −1/x2 dx = 1/x, ovvero 1/x + C1 per x > 0, 1/x + C2 per x < 0. •  ∫ (2x+1)/(x2+x+1) dx = log(x2+x+1)) + C  (x2+x+1) > 0 per ogni x).     Quindi il nostro intergrale vale 2·log(x) + 1/x + log(x2+x+1)) + C1 per x > 0, 2·log(−x) + 1/x − log(x2+x+1)) + C2 per x < 0.     A destra, in blu, il grafico dell'integranda e, in rosso, il grafico di un particolare integrale (per C1 = 0 e C2 = 0).

∫   x − 1  dx ——————— x2 (x2 + x + 1)2

Nel caso di questo integrale si procede come sopra, riscrivendo l'integranda così:

x − 1	=	A	+	B	+	Cx+D	+	Ex+F
———————		—		—		————		————
x2 (x2 + x + 1)2		x		x2		x2+x+1		(x2+x+1)2

∫   1  dx ——————— 2x2 − 12x + 26		Il denominatore non è scomponibile.

Procedo provando a completare il quadrato ( funzioni polinomiali):  2x²−12x+26 = 2(x²−6x+13) = 2((x²−6x+9)+4) = 2((x−3)²+4)
(x−3)²+4 = (((x−3)/2)² + 1) / 4.  t = (x−3)/2.  ∫ 1/(1+t²) dt = atna(t) (+c)
Quindi il nostro integrale vale  atan((x−3)/2) / 4 (+C). [verifica con R]

∫   3t2 + 2t + 2  dt —————— t3 + t2 + t

Inizio in modo simile al secondo esempio:

(3t²+2t+2) / (t³+t²+t) = (3t²+2t+2) / (t(t²+t+1)) =  ...  = t / (t²+t+1) + 2 / t

∫ 2/t dt = 2 log|t|       ∫ t / (t²+t+1) dt = ?     trasformo nella somma:

t / (t²+t+1) = (2t+1) / (t²+t+1) / 2 - 1 / (t²+t+1) / 2

∫ (2t+1) / (t²+t+1) dt = log(t²+t+1)     ∫ 1 / (t²+t+1) dt = ?   completo il quadrato:

(t + 1/2)² = t²+ t + 1/4     t²+ t + 1 = (t + 1/2)² + 3/4     u = t + 1/2   du = dt   a = √3/2

1 / (t²+t+1) = 1 / (u²+a²)     ∫ 1 / (u²+a²) du = arctan(u/a)/a

∫ 1 / (t²+t+1) dt = 2 arctan((2t+1)/√3)/√3   (t²+t+1 > 0 per ogni t)

∫ (3t²+2t+2) / (t³+t²+t) dt = 2 log(|t|) + log(t²+t+1)/2 − arctan((2t+1)/√3)/√3

dove è da intendersi che per t > 0 e per t < 0 si possono aggiungere due costanti diverse. [verifica con R]

Esercizi:   testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione

Si può dimostrare che ogni funzione razionale è integrabile mediante una combinazione lineare di funzioni razionali e di funzioni del tipo log(F(.)) e atn(F(.)) con F polinomio di primo o secondo grado.  Per trovare l'espressione dell'integrale si può usare WolframAlpha, mettendo in input integral (ed eventualmente selezionando l'opzione computation). 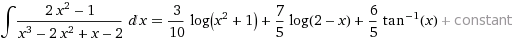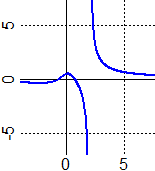Ecco ad esempio che cosa si ottiene per (2*x^2-1)/(x^3-2*x^2+x-2)     Occorre però osservare il grafico della funzione da integrare (vedi figura a lato) per individuare i vari intervalli in cui è definita la funzione ottenuta (in ciascuno dei quali va aggiunta una diversa "costante").

  Esiste vario software che calcola "simbolicamente" gli integrali indefiniti. Però, spesso, non dà tutte le soluzioni o ne dà alcune che valgono solo per particolari intervalli. Del resto, problemi analoghi valgono anche per alcuni procedimenti manuali suggeriti da alcuni libri.  Lo studio dei domini, il controllo grafico e/o simbolico di quanto si ottiene sono, dunque, fondamentali.

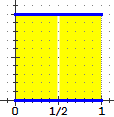
Osserviamo, infine, che accanto al concetto di integrale considerato qui, esistono altri concetti di integrazione, che consentono di definire l'area di altre superfici.  Consideriamo, ad esempio, la figura costituita dal quadrato che ha per lati i segmenti da 0 ad 1 dei due assi e privata dei segmenti costituiti dai punti di ascissa razionale; si può dimostrare (vedi i seguenti esercizi) che questi segmenti sono una infinità numerabile, trascurabile rispetto al complesso del quadrato; l'area di questa figura non può comunque essere calcolata mediante il concetto di integrale introdotto ( vedi). Attraverso un concetto più generale di integrale si può invece ottenere anche per tale figura, come per l'intero quadrato, che essa ha area 1. Chi proseguirà gli studi in matematica o fisica, o in corsi di laurea simili, studierà queste generalizzazioni, che hanno applicazioni in vari campi.

 altri collegamenti     [nuova pagina]