Altri usi degli integrali

  Il valor medio

Se conosco come varia la velocità v di un'automobile in un intervallo di tempo [a,b], che cosa intendo per velocità media:  la velocità costante a cui sarebbe andata per percorrere la strada nello stesso tempo.  Quindi il suo valore lo trovo dividendo la strada percorsa per il tempo impiegato.
La strada percorsa, ossia la differenza s(b)−s(a) tra la posizione finale e la posizione inziale  (per il teorema fondamentale del calcolo [ integrazione] essendo v(t) = s'(t))  è data da ∫[a,b] v(t) dt.     Quindi:    velocità media  =  ∫[a,b] v(t) dt / (b-a).     Passando da v a una generica funzione f continua positiva su [a,b], definiamo come valore medio di f in [a,b] l'altezza m del rettangolo di base [a,b] avente area uguale a quella compresa tra il grafico di f e l'intervallo [a,b].     Più in generale, se f è una qualunque funzione integrabile su [a,b], definiamo come valore medio di f in [a,b] il valore della funzione costante che ha su [a,b] lo stesso integrale, ossia: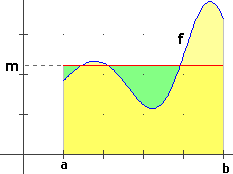
m =  ∫[a,b] f ——— b – a

    Si ha, facilmente, che vale un teorema del valor medio per gli integrali:

se f è continua su [a,b], esiste c in [a,b] in cui f assume il valore medio, ossia tale che:
f(c)  =  ∫_[a,b] f / (b-a).

    Nel caso della figura soprastante, vi sono tre di tali c:  le ascisse dei punti in cui il grafico di f taglia la retta di ordinata m.

    Il teorema del valor medio per le derivate ( propr. delle funzioni cont. e di quelle derivabili), applicato a una funzione integrale di f, mi avrebbe dato gli stessi punti. Nel caso della velocità, un istante c in cui essa assume il valor medio (rispetto alla integrazione) è anche un istante in cui s ha come derivata  (s(b)−s(a)) / (b−a).
    Il secondo degli esercizi seguenti illustra come si possa ricorrere a queste idee per determinare il centro di massa di un oggetto piano di spessore costante.

Esercizio 1 (e soluzione)       Esercizio 2 (e soluzione)

  Il volume

Generalizziamo alcuni metodi già visti ( il volume) per individuare il volume di una figura tridimensionale. Il particolare ci occuperemo delle figure che possono essere generate mediante la rotazione attorno ad un asse di una figura piana. Illustriamo le "tecniche" impiegabili partendo da un caso in cui sappiamo determinare il volume anche con altri metodi.

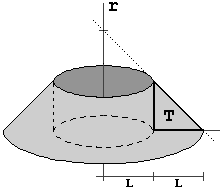
•  Determino il volume del solido raffigurato a lato, dotato di un asse di simmetria, con la superficie "interna" cilinidrica di raggio uguale all'altezza, una faccia a forma di corona circolare e il resto della superficie a profilo rettilineo, inclinato di 45° rispetto all'asse di simmetria (i semipiani aventi come bordo l'asse di simmetria intercettano sul solido dei triangoli rettangoli isosceli). L (la lunghezza dei cateti del triangolo T) è sia lo spessore della corona circolare che l'altezza e il raggio del cilindro.     Suppongo che L = 1, ossia uso come unità di volume L3. Posso pensare il solido come un cono circolare retto di altezza e raggio 2 da cui ho tolto un cono di altezza e raggio 1 e un cilindro circolare retto di altezza e raggio 1. Ottengo:  4π2/3-π/3-π = 4π/3 (ossia 4π/3L3).

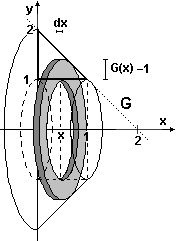
	•  Ora ricavo il volume usando direttamente qualche tecnica di integrazione. Dovrei ottenere lo stesso risultato.     Penso il solido come frutto della rotazione di una figura attorno all'asse di simmetria.     Nel mio caso posso pensare il profilo della figura − sia come grafico di una funzione F assumendo l'asse di rotazione come asse y − che come quello di una funzione G assumendo l'asse di di rotazione come asse x.
	Col secondo metodo (figura a sinistra) penso il solido come somma di tanti anelli (rondelle) di spessore Δx, raggio esterno G(x) e interno 1:
la variazione ΔV del volume al passare da x a x+Δx è approssimabile con π(G(x)2-1) (area della corona circolare base dell'anello) per Δx:  dV = π(G(x)2−1) dx.  G(x) = 2−x.  Dato che x varia in I = [0,1], il volume è V = ∫I π(3+x2−4x) dx = π(3x+x3/3−2x2)x=1 = π(3+1/3−2) = 4π/3.
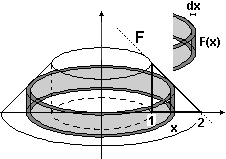
Col primo metodo (figura a destra) penso il solido come somma di cilindretti cavi (gusci cilindrici) di spessore Δx, raggio interno x e altezza F(x): la variazione ΔV del volume al passare da x a x+Δx è approssimabile con F(x)Δx (area del rettangolino dalla cui rotazione ottengo il cilindretto cavo) per 2πx (circonferenza del cilindretto):  dV = 2πxF(x)dx.  F(x) = 2−x (in questo caso particolare F(x)=G(x)).  Dato che x varia in I = [1,2], il volume è V = ∫I 2π(2x-x2)dx = 2π((x2−x3/3)x=2 − (x2−x3/3)x=1) = 2π(3−7/3) = 4π/3.

Vediamo altri due esempi.  Determiniamo il volume di una sfera in modo alternativo rispetto a quanto già visto ( il volume). Possiamo limitarci al caso in cui il raggio sia 1: moltiplicando per R3 il volume così ottenuto otterremo quello di una sfera di raggio R.  Penso la sfera come unione di dischi di spessore infinitesimo dx e raggio f(x) = √(1−x2), di volume π f(x)2dx = π(1−x2)dx.  Sommando il volume dei dischi ottengo: ∫[−1, 1] π f(x)2 dx = ∫[−1, 1] π(1−x2)dx = π ( [x−x3/3] x=1 − [x−x3/3] x=−1 ) = 4π/3.     In pratica, questo metodo dei dischi non è che un caso particolare del metodo delle rondelle.

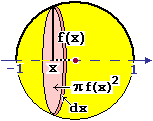    Osserviamo che, in modo simile, si può dimostrare che, più in generale, l'area dell'elissoide (x/a)²+(y/b)²+(z/c)² = 1 è 4/3·π·a·b·c.

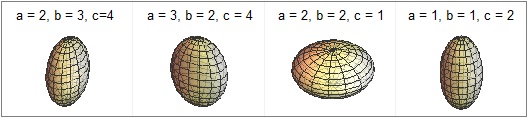
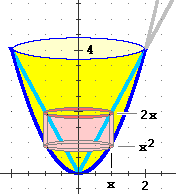Vediamo, ora, come ottenere il volume del solido a fianco (una specie di bicchiere), ottenuto ruotando attorno all'asse y la regione compresa tra y = 2x e y = x2 per x in [0, 2].     Potrei procedere come sopra, pensando il solido affettato orizzontalmente, come composto da tante rondelle. Procediamo, invece, pensandolo come composto da tanti gusci cilindrici di raggio x, altezza 2x−x2 e spessore dx.  "Sommando" il volume dei cilindri ottengo: ∫[0, 2] 2πx (2x−x2) dx = 2π ∫[0, 2] 2x2−x3 dx = 32π/3−8π = 8π/3.

Un solido di rotazione diffuso è la botte.  Se il profilo è parabolico, se D e d sono il diametro massimo e il diametro minimo (interni) ed h è l'altezza (interna), la capacità della botte è la seguente (come controllo, si noti che se d = D si ritrova il volume del cilindro): π·h·(3·d² + 4·d·D + 8·D²) / 60     Vedi qui per la dimostrazione. 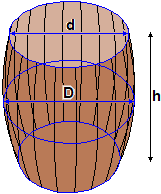Esercizio  (e soluzione)

  Lunghezza di un arco di curva

Abbiamo già visto ( lunghezza) come valutare la lunghezza del grafico di una funzione f continua definita su un intervallo chiuso e limitato [a, b]; abbiamo anche visto come, in particolari situazioni, questa lunghezza può essere infinita.  Consideriamo, ora, il caso particolare in cui f sia anche derivabile in [a, b], nel senso che ne esistano la derivata in (a, b) e le derivate sinistra e destra in a e in b [ propr. delle funz. continue e derivabili].  Suddividiamo [a, b] in n sottointervalli [x₀, x₁], [x₁, x₂], …, [x_n−1, x_n] dove a = x₀ < x₁ < … < x_n−1 < x_n = b.
    La poligonale che ne risulta approssima la nostra curva. Determiniamone la lughezza. Il k-esimo segmento è l'ipotenusa di un triangolo di base Δx_k ed altezza f(x_k)−f(x_k−1), e quindi è lungo:

Lk = √( Δxk2 + ( f(xk) − f(xk−1) )2 ) = √( 1 + ( ( f(xk) − f(xk−1) ) / Δxk)2 ) Δxk

Quindi (per il teorema del valor medio delle derivate: propr. funz, continue e funz. derivabili) esiste almeno un x_k*  in (x_k−1, x_k) tale che:

L_k = √( 1 + f '(x_k*)² ) Δx_k

Allora, aumentando n,  ∑_{k = 1..n} √( 1 + f '(x_k*)² ) Δx_k,  per quanto abbiamo già visto ( integrazione), converge a:

∫ _{[a, b]} √( 1 + f '(x)² ) dx

che assumiamo come lunghezza L del nostro arco di curva.

Esempio. Calcoliamo la lunghezza del grafico di x → x3/2, ovvero di x → √x3, per x tra 0 ed 1.  D(√x3)(x) = 3√x/2.  Quindi:   ∫ [0, 1] √(1+(3√x/2)2) dx  =  ∫ [0, 1] √(1+9x/4) dx  =   8/27·([(1+9x/4)3/2]x=1 − [(1+9x/4)3/2]x=0)  =   8/27·((13/4)3/2−1)  =  1.4397…

Controllo   con R:	G <- function(x) sqrt(1+(3*sqrt(x)/2)^2) # ovvero: # f <- function(x) x^(3/2); g <- function(x) eval(D(body(f),"x")) # G <- function(x) sqrt(1+g(x)^2) integrate(G,0,1)   1.43971 with absolute error < 1.6e-14 8/27*((13/4)^1.5-1)   1.43971 Caricando la libreria "codetools" col comando "showTree" posso ottenere un arrotondamento a 15 cifre (occorre tener conto degli eventuali errori di arrotondamento) library(codetools) showTree(8/27*((13/4)^1.5-1))   1.43970987337155 # se vuoi avere più cifre anche del valore calcolato da integrare: showTree(integrate(G,0,1)$value)   1.43970987337155 # ovvero, senza caricare codetools: print(integrate(G,0,1)$value, 16)   1.43970987337155
O, senza usare il calcolo differenziale:	Usando questo semplice script. O: source("http://macosa.dima.unige.it/r.R") f <- function(x) x^(3/2) lungFun(f, 0,1, 500) # 1.439709 lungFun(f, 0,1, 2000) # 1.43971
Con wolframalpha:	Seleziono la voce arc length , quindi a formula;  metto nel box curve sqrt(x^3),  nel box lower limit 0 e nel box upper limit 1.  Ottengo:   1/27*(-8+13*sqrt(13)) = 1.4397098733715504…  Ovvero batto direttamente curve y=sqrt(x^3), x = 0..1  Posso calcolare anche la lunghezza di curve in coord. polari:  polar plot t, t = 0..2*pi

Esercizio  (e soluzione)

  Nel caso in cui la curva sia data nella forma parametrica  x = f(t), y = g(t) per t in [a,b]  si ha in modo simile che la lunghezza di essa è:

∫ _{[a, b]} √( f '(t)² + g '(x)² ) dt

    Evidentemente, per g(t)=t rientriamo nella situazione considerata nel paragrafo precedente.

Esercizio  (e soluzione)

  Calcolo dei momenti di inerzia

    Vai qui per l'uso dell'integrazione per calcolare il momento di inerzia (e il centroide) di vari corpi.