Integrazione di funzioni razionali

Illustriamo i procedimenti che si possono impiegare per integrare le cosiddette funzioni razionali, ossia le funzioni esprimibili come rapporto tra funzioni polinomiali, attraverso alcuni esempi.

∫   3x3−2x2−19x−7  dx ——————— x2−x−6

Innanzi tutto trasformo il rapporto eseguendo la divisione in modo di ricondurmi ad un rapporto in cui il primo termine abbia grado minore:

3 2 2 3 x - 2 x - 19 x - 7 | x - x - 6 ----------- 3 2 3 2 | 3 x [ <-- 3x / x ] 3 x - 3 x - 18 x | -------------------- | 2 | 2 2 x - x - 7 | 1 [ <-- x / x ] 2 | x - x - 6 | ------------- | - 1

∫ (3x³−2x²−19x−7) / (x²−x−6) dx = ∫ 3x+1 + (−1) / (x²−x−6) dx = ∫ 3x+1 dx − ∫ 1 / (x²−x−6) dx.
Il primo integrale so che fa  3x²/2+x (+c).
x²−x−6  posso scomporlo in (x+2)(x−3), per cui posso dedurre che  1 / (x²−x−6)  può essere scomposto additivamente come  A/(x+2) + B/(x−3).  Eguagliando i due termini trovo  1 = A(x−3) + B(x+2), ovvero  1 = (A+B)x + 2B−3A,  da cui A = −B, B = 1/5.
Quindi  ∫ 1 / (x²−x−6) dx = ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx. Il dominio è costituito dall'unione degli intervalli (−∞, −2), (−2, 3), (3, ∞). Nel primo intervallo  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(−x−2)/5 + log(3−x)/5 (+ c1), nel secondo  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(x+2)/5 + log(3−x)/5 (+ c2), nel terzo  ∫ −(1/5) / (x+2) + (1/5) / (x−3) dx = −log(x+2)/5 + log(x−3)/5 (+ c3).

Perciò l'integrale della funzione iniziale è  3x2/2+x+log(−x−2)/5−log(3−x)/5 (+c1) per x in (−∞,−2), 3x2/2+x+log(x+2)/5−log(3−x)/5 (+c2) per x in (−2,3), 3x2/2+x+log(x+2)/5−log(x−3)/5 (+c3) per x in (3,∞).
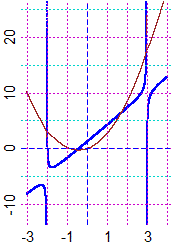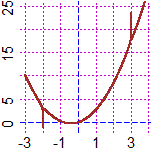	Potremmo esprimere l'integrale come  3x2/2+x+log(|x+2|)/5−log(|x−3|)/5, ovvero come  3x2/2 + x + log(|(x+2)/(x−3)|) / 5  in ognuno dei tre intervalli, in ciascuno dei quali si possono aggiungere diverse costanti.  A destra in blu è raffigurata la funzione da integrare e, in marrone, i grafici dei tre rami di curva che, a meno di innalzamenti o abbassamenti, ne rappresentano l'integrale.  Questi sono ripresi a sinistra, evidenziandone meglio il loro comportamento presso -2 e 3. [verifica con R]. Vedi in fondo come fare il calcolo con WolframAlpha.

∫   x − 1  dx —————— x2 (x2 + x + 1)

Consideriamo l'integrale a sinistra.

x²+x+1 è irriducibile. Cerco di riscrivere l'integranda così:

x − 1	=	A	+	B	+	Cx+D	Ho:  x−1 = Ax(x2+x+1)+B(x2+x+1)+(Cx+D)x2
——————		—		—		————
x2 (x2 + x + 1)		x		x2		x2+x+1

Raccogliendo i termini ottengo A+C = 0, A+B+D = 0, A+B = 1, B = −1,  da cui: A = 2, B = −1, C = −2, D = −1.  Quindi ho ricondotto l'integrale di partenza a  ∫ 2/x − 1/x² − (2x+1)/(x²+x+1) dx.

•  ∫ 2/x dx = 2·log(|x|), ovvero ∫ 2/x dx = 2·log(x) + C1 per x > 0, ∫ 2/x dx = 2·log(−x) + C2 per x < 0. •  ∫ −1/x2 dx = 1/x, ovvero 1/x + C1 per x > 0, 1/x + C2 per x < 0. •  ∫ (2x+1)/(x2+x+1) dx = log(x2+x+1) + C  (x2+x+1) > 0 per ogni x).     Quindi il nostro intergrale vale 2·log(x) + 1/x + log(x2+x+1) + C1 per x > 0, 2·log(−x) + 1/x − log(x2+x+1) + C2 per x < 0.     A destra, in blu, il grafico dell'integranda e, in rosso, il grafico di un particolare integrale (per C1 = 0 e C2 = 0). Vedi qui per una verifica con R.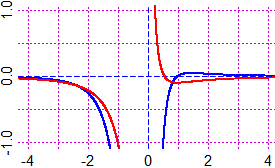

∫   x − 1  dx ——————— x2 (x2 + x + 1)2

Nel caso di questo integrale si procede come sopra, riscrivendo l'integranda così:

x − 1	=	A	+	B	+	Cx+D	+	Ex+F
———————		—		—		————		————
x2 (x2 + x + 1)2		x		x2		x2+x+1		(x2+x+1)2

∫   1  dx ——————— 2x2 − 12x + 26		Il denominatore non è scomponibile.

Procedo provando a completare il quadrato:  2x²−12x+26 = 2(x²−6x+13) = 2((x²−6x+9)+4) = 2((x−3)²+4)
(x−3)²+4 = (((x−3)/2)² + 1) / 4.  t = (x−3)/2.  ∫ 1/(1+t²) dt = atna(t) (+c)
Quindi il nostro integrale vale  atan((x−3)/2) / 4 (+C). [verifica con R]

∫   3t2 + 2t + 2  dt —————— t3 + t2 + t

Inizio in modo simile al secondo esempio:

(3t²+2t+2) / (t³+t²+t) = (3t²+2t+2) / (t(t²+t+1)) =  ...  = t / (t²+t+1) + 2 / t

∫ 2/t dt = 2 log|t|       ∫ t / (t²+t+1) dt = ?     trasformo nella somma:

t / (t²+t+1) = (2t+1) / (t²+t+1) / 2 - 1 / (t²+t+1) / 2

∫ (2t+1) / (t²+t+1) dt = log(t²+t+1)     ∫ 1 / (t²+t+1) dt = ?   completo il quadrato:

(t + 1/2)² = t²+ t + 1/4     t²+ t + 1 = (t + 1/2)² + 3/4     u = t + 1/2   du = dt   a = √3/2

1 / (t²+t+1) = 1 / (u²+a²)     ∫ 1 / (u²+a²) du = arctan(u/a)/a

∫ 1 / (t²+t+1) dt = 2 arctan((2t+1)/√3)/√3   (t²+t+1 > 0 per ogni t)

∫ (3t²+2t+2) / (t³+t²+t) dt = 2 log(|t|) + log(t²+t+1)/2 − arctan((2t+1)/√3)/√3

dove è da intendersi che per t > 0 e per t < 0 si possono aggiungere due costanti diverse. [verifica con R]

Esercizi:   uno     due     tre

Si può dimostrare che ogni funzione razionale è integrabile mediante una combinazione lineare di funzioni razionali e di funzioni del tipo log(F(.)) e atn(F(.)) con F polinomio di primo o secondo grado.  Per trovare l'espressione dell'integrale si può usare WolframAlpha, mettendo in input integral (ed eventualmente selezionando l'opzione computation). Ecco ad esempio che cosa si ottiene per (2*x^2-1)/(x^3-2*x^2+x-2) integral (2*x^2-1)/(x^3-2*x^2+x-2) dx     Occorre però osservare il grafico della funzione da integrare (vedi figura a lato) per individuare i vari intervalli in cui è definita la funzione ottenuta (in ciascuno dei quali va aggiunta una diversa "costante").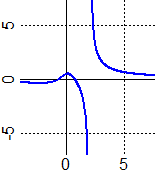