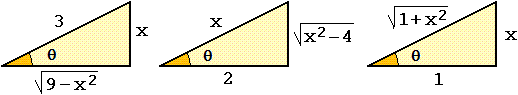
Integrazione per sostituzione trigonometrica

Esisitono alcuni "trucchi" per calcolare con sostituzione alcuni tipi particolari di integrali, in cui si utilizzano le relazioni tra gli elementi di un triangolo rettangolo (tuttavia, anche in questi casi, esiste del software che esegue automaticamente i calcoli).  Facciamo degli esempi, riferendoci alle figure seguenti (che valgono solo per x e θ positivi, ma suggeriscono relazioni che possono valere anche per x e θ negativi).

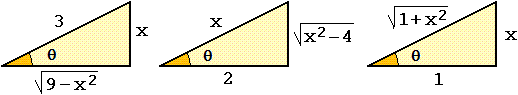
∫ 1/√(9−x2) dx     può essere affrontato (vedi figura a sinistra) pensando a  √(9−x2) = 3·cos(θ),  x = 3·sin(θ),  dx = 3·cos(θ) dθ ∫ 3·cos(θ) / (3·cos(θ)) dθ = ∫ 1 dθ = θ ∫ 1/√(9−x2) dx = asin(x/3)  (+c)   (a destra il controllo "grafico")		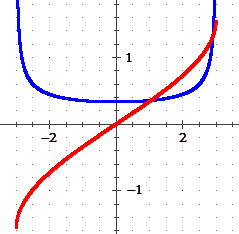x → 1/√(9−x2) x → asin(x/3)
∫ 1 / ( √(x2−4) x2 ) dx     può essere affrontato (vedi figura sopra al centro) pensando a  √(x2−4) = 2·tan(θ),  2/x = cos(θ), da cui  x = 2/cos(θ), dx = 2·tan(θ)/cos(θ) dθ.

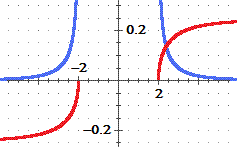Quindi  ∫ 1 / (2·tan(θ)·4/cos(θ)2)·2·tan(θ)/cos(θ) dθ = ∫ 1/4 cos(θ) dθ = sin(θ)/4 (+c) ∫ 1 / ( √(x2−4) x2 ) dx = √(x2−4) / (4x) (+c)   (a sinistra il controllo "grafico") x → 1 / ( √(x2−4) x2 )    x → √(x2−4) / (4x)

∫ _{[−1, 1]} 1 / (1+x²)² dx   è un integrale definito che possiamo affrontare considerando il triangolo rettangolo raffigurato sopra a destra:
x = tan(θ),  1/√(1+x²) = cos(θ),  dx = 1/cos(θ)² dθ.  Per x che varia tra −1 e 1  θ varia tra −π/4 e π/4.
∫ _{[−1, 1]} 1 / (1+x²)² dx = ∫ _{[−π/4, π/4]} cos(θ)⁴ / cos(θ)² dθ = ∫ _{[−π/4, π/4]} cos(θ)² dθ = ∫ _{[−π/4, π/4]} (1−cos(2θ))/2 dθ = [(θ+sin(2θ)/2)/2] _{θ = −π/4 .. π/4} = π/4 + 1/2.

Controllo numerico con R:   f <- function(x) 1/(1+x^2)^2; integrate(f,-1,1); pi/4+1/2]

Esercizio