Alcuni momenti di inerzia

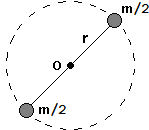
    Abbiamo visto ( indici di posizione e di dispersione) che il momento di inerzia (ossia la grandezza fisica scalare che esprime l'inerzia al cambiamento della velocità di rotazione) di una masserella di massa m che ruota descrivendo un cerchio di raggio r attorno ad un punto O è m·r².
    Nel caso di più masserelle lo si ottiene sommando i momenti di inerzia delle singole masserelle. Nel caso particolare illustrato sotto al centro esso è ancora m·r².
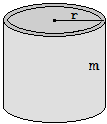
    Ovviamente il cilindro cavo di massa m e raggio r raffigurato sotto a destra ha lo stesso momento di inerzia attorno al suo asse, m·r².

    Nel caso di un disco, come quello raffigurato sotto a sinistra, per calcolare il momento di inerzia rispetto all'asse di rotazione rappresentato in rosso, devo fare la somma dei momenti di inerzia di tanti (anzi, infiniti) anelli, dei quali, se m₁, m₂, … fossero le loro masse e r₁, 2₂, … le loro distanze dal centro, avremmo I_i = m_i·r_i².  Esprimiamo le masse m_i in funzione del raggio r_i. Sia ρ la densità superficiale del disco, ρ = m/(πR²).
    L'area di un anello di spessore d r è 2πr_i·d r.  Quindi m_i = ρ·2πr_i·d r = m/(πR²)·2πr_i·d r = 2m/R²·r_i·d r.  In definitiva I_i = m_i·r_i² = 2m/R²·r_i³·d r.
    Per "sommare" passiamo all'integrale ( altri usi degli integrali):

I = ∫ _{[0, R]} 2m/R²·r³·d r = 2m/R² ∫ _{[0, R]} ·r³·d r = 2m/R²·R⁴/4 = m·R² / 2.

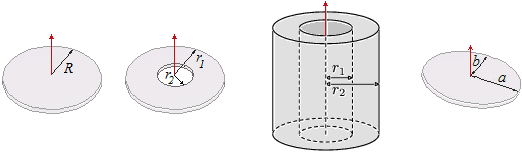
    Con calcoli del tutto analoghi (cambiano solo gli estremi di integrazione) abbiamo che per il disco bucato (raffigurato a sopra, a destra del disco pieno) e per il disco bucato (raffigurato al suo fianco)  I = m·(r₁² − r₂² ) / 2.  Con calcoli simili a quelli per il disco circolare, per il disco ellittico si ottiene  I = m·(a² + b² ) / 4  (quando a = b = R si riottiene il momento di inerzia del disco circolare).

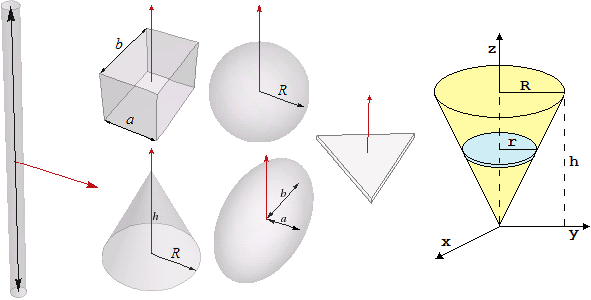
    Ecco i momenti di inerzia di alcuni solidi di materiale omogeneo di forme comuni rispetto agli assi di rotazione rappresentati in rosso:  quello di una sbarra sottile lunga L è  m·L²/12,  quello di una parallelepipedo (o un rettangolo) con lati perpendicolari all'asse di rotazione lunghi a e b è  m·(a²+b²)/12,  quello di una sfera di raggio R è  2·m·R²/5,  quello di un elissoide di semiasssi a e b è  m·(a²+b²)/5,  quello di un triangolo di lati a, b e c è  m·(a²+b²+c²)/36.   A destra una figura da utilizzare come traccia per dimostrare che il momento di inerzia del cono è quello indicato sopra.

    Nel caso di oggetti tridimensionali dalle forme comuni è facile determinarne il centroide, che, se l'oggetto è di materiale omogeneo, coincide col baricentro.  Abbiamo visto come determinare il centroide (a,b,c) di figure di spessore costante (qui, qui, qui e qui): immaginando la figura appoggiata sul piano (x,y), si prende come (a,b) il centroide della superficie e si prende come c metà dello spessore.  Se la figura ha un piano di simmetria il centroide sta in esso. Quindi nel caso di una sfera il centroide coincide con il centro (gli infiniti piani di simmetria passano tutti per esso), cosa analoga può dirsi per un elissoide. Vediamo come trovarlo nel caso di una piramide e di un cono.

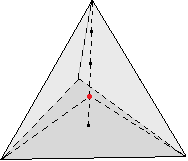
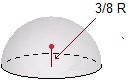
È stato Leonardo da Vinci a trovare che nel caso di una piramide il suo centroide, comunque si scelga la base, si trova sulla congiungente il vertice col centroide della base ad 1/4 da questa (figura qui a destra).  Analogamente il centroide di un cono si trova sulla coniungente il vertice col centroide della base ad 1/4 da questa.  Nel caso di mezza sfera di trova a 3/8 del raggio perpendicolare al cerchio di base (figura a sinistra).     Invece, nel caso di una superficie a forma di cono circolare retto (ossia della sua superficie laterale) si trova a 1/3 dell'altezza (a partire dalla base) e in quello di una superficie semisferica si trova a metà altezza.  Per approfondimenti ed esercizi vedi qui (in: Physics 107 → Outline of Material Covered → Momentum).