Altre leggi di distribuzione

  Un esempio

Un esempio "fantastico" per introdurre impieghi "concreti":

ogni secondo arriva uno zombie di fronte a un muro lungo 1 in cui è praticata un'apertura ampia w; gli zombie che non passano attraverso l'apertura, dopo la facciata contro il muro si rialzano e si predispongono a ritentare l'avventura, per cui il flusso di zombie è senza fine, e sempre con lo stesso regime; inoltre:

(1)   le posizioni lungo il muro in cui arrivano gli zombie hanno distribuzione uniforme (non viene privilegiata alcuna parte del muro), per cui, ovunque sia collocata l'apertura, per essa c'è un flusso stazionario di zombie (la media teorica del numero di zombie N_w che passano in un intervallo di tempo fissato è proporzionale a w:  M(N_w)=λw);

(2)   la posizione di arrivo di ogni zombie è indipendente da quella di ciascuno dei precedenti, cioè siamo di fronte a un flusso senza memoria;

(3)   è trascurabile la probabilità che due o più zombie arrivino praticamente nella stessa posizione, cioè, al rimpicciolire dell'apertura, la differenza relativa tra Pr(1≤N_w) e Pr(N_w=1) tenda ad annullarsi  (per w → 0 Pr(N_w=1)/Pr(1≤N_w) → 1);  in casi come questo si parla di flusso ordinario.

Si può simulare il fenomeno usando generatore di numeri pseudocasuali ( calc. delle probabilità). Basta indicare con w la ampiezza della apertura e ogni secondo eseguire l'istruzione che in R ha la forma: if(runif(1) < w) U <- 1 else U <- 0 U = 1  indica il passaggio dello zombie per l'apertura        (evento con probabilità  w = AmpiezzaApertura / LunghezzaMuro), U = 0  il non passaggio.

    Infatti il generatore di numeri pseudocasuali verifica (1) e (2), come abbiamo già osservato, e (come si può controllare sperimentalmente) verifica anche (3).

    Sviluppando questa idea è stato realizzato il programma Zombie ( zombie, apribile da Windows), che simula il fenomeno nel caso in cui w = 1/10.  Il programma ha diverse modalità di funzionamento. Man mano che arrivano gli zombie, esso costruisce sia l'istogramma di distribuzione (in intervalli ampi 1 sec) dei tempi di attesa tra un passaggio per l'apertura e il passaggio successivo (a colonne verticali), sia quello di quanti zombie passano per l'apertura in 60 secondi (a colonne orizzontali).  Ecco un possibile stato finale del programma (8 ore e mezza simulate in pochi istanti). Ogni crocetta a sinistra (tempi di attesa) rappresenta 16 uscite, ogni crocetta a destra (zombi che passano) rappresenta 4 uscite (qui puoi vedere qualche passo per arrivare ad esso).

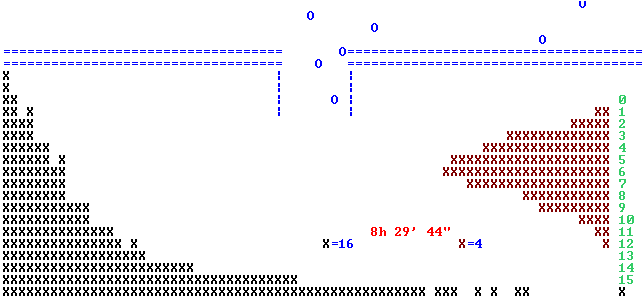
    Come si vede, l'istogramma a sinistra, dei tempi di attesa, ha, grosso modo, andamento decrescente, simile all'istogramma della () distribuzione esponenziale negativa. Quello degli zombi che passano ogni minuto ha un andamento a campana asimmetrica, che ha qualche somiglianza con una binomiale (). Qui trovi come effettuare lo stesso studio con R. Nel prossimo paragrafo approfondiremo lo studio di questa somiglianza.

  Le leggi esponenziale e di Poisson

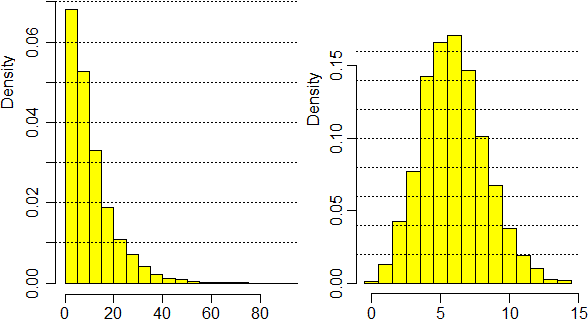
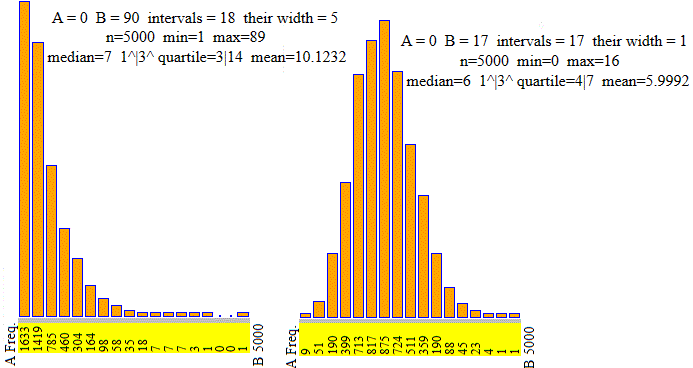
Ecco l'analisi statistica (effettuata col programma R, nel modo descritto nel file a cui si è rinviati alla fine del paragrafo precendente) di 48 ore di arrivi di zombie. Supponiamo di aver dato i nomi T-Zombie e N-Zombie alle due sequenze di dati.

Min. 1stQu. Median Mean 3rdQu. Max. 1.00  3.00  7.00  10.06 14.00 92.00 n.dati = 17183; s.q.m.= 9.367475	Min. 1stQu. Median Mean 3rdQu. Max.  0.000 4.000 6.000 5.966 7.000 14.000  n.dati = 2880; s.q.m.= 2.30908

Ecco l'analisi effettuata con questi script (con 5000 prove):

    L'analisi di T-Zombie (a sinistra) rafforza l'idea che la differenza temporale D_w tra due successivi passaggi per l'apertura abbia distribuzione esponenziale negativa, come nel caso dei tempi di attesa tra una telefonata e l'altra nella situazione considerata alla voce leggi di distribuzione (variabili continue). Ciò è suggerito sia dalla forma dell'istogramma, sia dal fatto che scarto quadratico medio e media siano quasi uguali:  U con distribuzione esponenziale negativa ha M(U )= σ(U).

    Si può dimostrare teoricamente che, nelle ipotesi fatte, D_w  (sopra studiata statisticamente)  ha effettivamente funzione di densità x → w·e^−wx  (e funzione di ripartizione x → 1 e ^wx)  con w = ampiezza della apertura del muro, cioè con 1/w = tempo di attesa medio (in sec).

    L'andamento dell'istogramma di N-Zombie (a destra) è simile a quello di una binomiale non simmetrica. In realtà si può dimostrare che, fissata una durata di tempo T (in sec), il numero di zombie N_w che passano per l'apertura in un intervallo di tempo ampio T ha legge di distribuzione:

Pr(Nw= n) =	an	e–a		con  a = numero medio di zombie che passano per l'apertura nel tempo T
	——
	n!

Poiché nel nostro caso T = 60, a = wT = 6.

    È una funzione (di n) che all'inizio sale quasi esponenzialmente, poi scende, quando n! prevale su aⁿ.  Essendo una legge di distribuzione abbiamo:

Pr(N_w=0) + Pr(N_w=1) + Pr(N_w=2) + … = 1,  e quindi:
e^−a · (1 + a + a²/2 + a³/3! + a⁴/4! + …) = 1.  Dunque dev'essere:
1 + a + a²/2 + a³/3! + a⁴/4! + … = e^a.

    Avevamo già visto che, per x → 0, e^x = x + 1 + o(x). In effetti si può dimostrare che vale anche  e^x = x + 1 + x²/2 + o(x²), anzi che  e^x = x + 1 + x²/2 + x³/3! + o(x³), e così via.  Non vedremo qui la dimostrazione di questo fatto.

    Osserviamo che Pr(N_w=0), valore che esprime la probabilità che non passino zombie, deve essere uguale a Pr(D_w>T), cioè alla probabilità che la differenza temporale tra due passaggi sia maggiore di T.

    Verifichiamolo:  Pr(N_w=0) = e ^a;  Pr(D_w>T) = 1 Pr(D_w≤T) = 1 (1 e^-wT) = e^-wT = e ^a.

    Questa legge di distribuzione si chiama legge di Poisson (di parametro a - spesso il parametro viene indicato con la lettera greca λ, "lambda").

    Qui puoi vedere come tracciare con R il grafico di una legge di Poisson e come confrontarlo con esiti sperimentali come i precedenti.

    Si può dimostrare che M(N_w) = Var(N_w) = a.

    Ciò è in accordo con gli esiti sperimentali, riportati sopra:  media = 6.119;  s.q.m. = 2.39; √6.119 = 2.49.

    Verifichiamo graficamente la corrispondenza di questa legge con l'istogramma sperimentale.

All'aumentare del parametro la "poissoniana" tende ad assumere andamento simmetrico a campana. Si vedano i grafici a destra, relativi ad a = 6 e a = 12.     Abbiamo già osservato che la curva poissoniana assomiglia a una binomiale. In effetti si può dimostrare che la legge di Poisson approssima la legge binomiale Bn,p con n·p = a, e che, fissato a, questa approssimazione migliora al crescere di n  (la poissoniana, quindi, come la bernulliana, tende a confondersi con una curva di Gauss, e con questa spesso può essere approssimata).

    In altre parole l'approssimazione migliora man mano che p (=a/n) tende a 0, cioè più è raro l'evento di cui conto il verificarsi nelle n prove ripetute. Per questo a volte la legge di Poisson viene anche chiamata legge degli eventi rari.

  L'impiego della legge di Poisson è frequente. Infatti sono molte le situazioni che si comportano analogamente alla situazione degli "zombie", cioè in cui si ha a che fare con:

(1)   elementi che si distribuiscono uniformemente in un certo "spazio",

(2)   cadendo in modo stocasticamente indipendente in sottospazi disgiunti, e

(3)   tendenzialmente, senza sovrapporsi.

e si vuole valutare la probabilità che cada una certa quantità di elementi in una porzione di spazio di dimensione w fissata, noto il numero medio a di elementi che cadono in una porzione di dimensione w.

Esempio. Una lamiera presenta dei piccoli difetti che si collocano in modo soddisfacente le condizioni sopra descritte, con densità di 0.03 difetti per cm². La probabilità che un pezzo di 10 cm² abbia almeno un difetto è: 1 Pr(N_w=0) = 1 e ^0.3 = 0.259; infatti a = 0.03 10 = 0.3.

  Anche le situazioni di "eventi rari" possono essere interpretate in questo modo.
    Consideriamo, ad esempio, un campione radioattivo che contenga 2.5 10²¹ nuclei; ogni nucleo abbia, in ogni istante, la probabilità 5.2 10^-21 di decadere entro 1 minuto; vogliamo trovare qual è la probabilità che il numero N dei decadimenti in un minuto sia 2. Dovremmo assegnare ad N la legge B_n,p con n=2.5 10²¹ e p=5.2 10^-21 (n è praticamente costante), ma ci troveremmo di fronte ad elevamenti alla potenza proibitivi.
    Per quanto osservato sopra possiamo approssimare questo valore usando la legge di Poisson con a = np = 13:  Pr(N=2) = 13²/2·e^-13=1.91 10^-4.  Ma anche senza passare attraverso la binomiale potevano osservare che gli atomi decadono in tempi che si succedono rispettando le condizioni (1) (3) (ad esempio la (1) corrisponde al fatto che l'emissione di elettroni è più o meno costante),  e che il numero medio (a) di nuclei che decadono nel tempo di 1 minuto (w) è np.

Esercizio  (soluz.)       Esercizio  (soluz.)       Esercizio  (soluz.)

Vedi qui per un uso di R impiegando la libreria source("http://macosa.dima.unige.it/r.R").

 altri collegamenti     [nuova pagina]