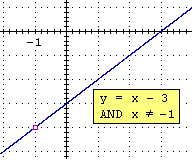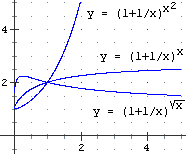Limiti
 La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che:
La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che:
– l'intervallo [3,∞) non ha limiti superiori,
– un punto che procede oltre ogni limite in una direzione fissata descrive una semiretta,
– un angolo è una figura illimitata (cioè che si estende senza limitazioni),
– un espressione decimale illimitata prosegue dopo il "." con una sequenza infinita di cifre,
– una successione è una sequenza illimitata di oggetti matematici,
– il numero delle copie fatte mensilmente con una fotocopiatrice non può aumentare oltre ogni limite.
In questi casi, come anche in molti contesti non matematici («a tutto c'è un limite», «se il livello dell'acqua del bacino scende sotto al limite di guardia scatta il razionamento dell'acqua», …), "limite" indica qualcosa che non può essere superato. È un significato abbastanza simile a quello che viene dato alla parola quando si parla dei  "limiti di un modello": si intende indicare che esso deve essere usato tenendo conto delle semplificazioni operate, stando attenti a non estendere troppo le conclusioni basate sull'analisi di esso.
"limiti di un modello": si intende indicare che esso deve essere usato tenendo conto delle semplificazioni operate, stando attenti a non estendere troppo le conclusioni basate sull'analisi di esso.
In altre situazioni la parola limite viene usata con un significato un po' diverso: «dopo qualche oscillazione la sua frequenza di pedalata si è stabilizzata su un valore limite che, se mantenuto, dovrebbe consentirgli di battere il precedente record», «che sia inizialmente più caldo o più freddo non importa: la stanza raggiungerà al limite la temperatura su cui è posizionato il termostato del condizionatore», «al riempirsi del recipiente il galleggiante sale e l'asta a cui è fissato raggiunge gradualmente una posizione limite orizzontale», «dopo l'apertura del paracadute ha incominciato a frenare, e la velocità di caduta si è progressivamente stabilizzata sul valore limite di 20 km/h», ….
Si tratta di casi in cui stiamo considerando un certo processo che evolve verso una condizione limite; qui usiamo "limite" nel senso di uno stato che un certo fenomeno tende ad assumere.
|
La figura sottostante dovrebbe chiarire la differenza tra i due usi. Se a una pallina di gomma immersa in un secchio d'acqua dò una piccola spinta verso il basso la pallina incomincia a oscillare: il suo centro sale, poi scende, poi sale, …. |
| 1) Se durante una particolare oscillazione il suo centro sta entro due posizioni L1 e L2, siamo sicuri che durante l'evoluzione del fenomeno esso non le supererà: L1 e L2 sono un limite inferiore e uno superiore alla posizione che potrà assumere il centro della pallina. |  |
2) Al passare del tempo le oscillazioni si smorzano e il centro della pallina tende ad assumere una particolare posizione limite L.
Nel primo caso "limite" indica una limitazione (i matematici a volte usano le espressioni "minorante" e "maggiorante" per indicare valori che, come i numeri che esprimono i livelli L1 e L2, sono minori o maggiori di tutto un certo insieme di valori). Nel secondo caso indica lo stato L su cui tende a stabilizzarsi il processo. |
 Soffermiamoci sul secondo uso ("limite" come stato a cui tende un processo), che è quello più frequente in matematica. In voci precedenti si sono già incontrati molti contesti a cui esso può essere applicato:
Soffermiamoci sul secondo uso ("limite" come stato a cui tende un processo), che è quello più frequente in matematica. In voci precedenti si sono già incontrati molti contesti a cui esso può essere applicato:
| • | Le successive approssimazioni per troncamento della radice quadrata di un numero – generate con un algoritmo come quello descritto alla voce  funzione(1) – hanno come limite la radice quadrata del numero; nel caso a lato abbiamo una successione di numeri limitati che tende a √5. funzione(1) – hanno come limite la radice quadrata del numero; nel caso a lato abbiamo una successione di numeri limitati che tende a √5. | | | 2 | | 2.2 | | 2.23 | | 2.236 | | ··· | | 2.236067977 | | 2.2360679774 | | ··· | | → √5 |
|
| • | Quando descriviamo il numero periodico 3.777… con (1) scrivi "3.", (2) scrivi "7", (3) ritorna a (2) intendiamo indicare l'espressione "limite" a cui tende questo processo di scrittura, che non potremo mai completare ( numeri).
Analogamente, la somma e il prodotto delle approssimazioni di due numeri x e y all'aumentare del numero delle cifre significative tendono, rispettivamente, al valore esatto di x+y e di x·y ( numeri).
Analogamente, la somma e il prodotto delle approssimazioni di due numeri x e y all'aumentare del numero delle cifre significative tendono, rispettivamente, al valore esatto di x+y e di x·y ( strutture numeriche). strutture numeriche). |
| • | Nel caso della produzione di un bene che sia descrivibile con un modello del tipo di quello rappresentato a fianco (il costo unitario è costituito da 5 centesimi di euro di costi incorporati e da una frazione dei 30 mila euro di costi fissi), all'aumentare del numero n dei pezzi prodotti il costo unitario tende a coincidere con i costi incorporati. Analogamente, nel caso dell'impiego di una chiave da meccanico per svitare un bullone, all'aumentare della distanza dell'impugnatura dal bullone (ipotizzando l'esistenza di chiavi lunghe a piacere) la forza da esercitare tende a zero ( proporzionalità inversa). proporzionalità inversa). | | 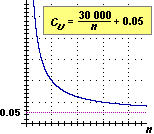 |
| • | Nel caso in cui le lunghezze di approssimazioni poligononali di un arco di curva man mano più fitte tendono a stabilizzarsi su un certo valore, assumiamo questo limite come lunghezza dell'arco di curva ( lunghezza). lunghezza). | | 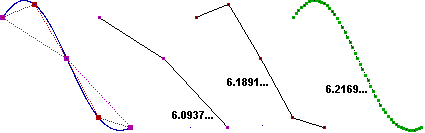 |
| • | L'area di un cerchio di lato 1 è il limite della successione delle aree delle figure costituite dai quadretti di lato 0.1, 0.01, 0.001, … (disposti nel modo raffigurato a lato) contenuti in esso ( area): area):
2.76, 3.1016, 3.137548, … → π | | 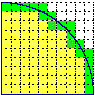 |
| • | Ripetendo il lancio di due dadi la frequenza relativa con cui esce un numero maggiore di 7 tende a stabilizzarsi sulla probabilità (41.666…%) che lanciando due dadi l'uscita sia maggiore di 7; nella tabella a lato n è il numero dei lanci ( calcolo delle probabilità). calcolo delle probabilità). | |
n frequenza
1 0%
2 50%
3 33.33333%
... ...
1000 40.1%
... ...
100000 41.724%
... ... |
 In matematica si usano delle notazioni e dei modi di dire per descrivere in modo conciso fenomeni come questi. Prendiamo ad esempio il caso di
In matematica si usano delle notazioni e dei modi di dire per descrivere in modo conciso fenomeni come questi. Prendiamo ad esempio il caso di  CU in funzione di n; il fatto che all'aumentare di n (nell'ipotesi ideale che il volume di produzione possa aumentare a piacere e senza modifiche dei costi fissi) 30000/n + 0.05 tende a stabilizzarsi su 0.05 può essere espresso con:
CU in funzione di n; il fatto che all'aumentare di n (nell'ipotesi ideale che il volume di produzione possa aumentare a piacere e senza modifiche dei costi fissi) 30000/n + 0.05 tende a stabilizzarsi su 0.05 può essere espresso con:
| • per n che tende all'infinito 30000/n + 0.05 tende a 0.05 |
| • il limite di 30000/n + 0.05 per n che tende all'infinito è 0.05 |
| • 30000/n + 0.05 → 0.05 per n → ∞ |
| • 30000/n + 0.05 → 0.05 | | n → ∞ |
|
| • lim 30000/n + 0.05 | = 0.05 | | n → ∞ |
|
Al posto dell'ultima scrittura si usa anche (per comodità tipografica) lim n → ∞ 30000/n+0.05 e, ove non fosse chiara la delimitazione di ciò di cui si fa il limite, lim n → ∞(30000/n+0.05).
Considerando lo stesso fenomeno, osserviamo anche che man mano che diminuisce il numero n dei pezzi prodotti aumenta la frazione 30000/n dei costi fissi che incide sul costo unitario:
| n | CU = 30000 / n + 0.05 |
| 1 000 000 | 0.03+0.05 = 0.8 |
| 100 000 | 0.3+0.05 = 0.35 |
| 10 000 | 3+0.05 = 3.05 |
| 1 000 | 30+0.05 = 30.05 |
| 100 | 300+0.05 = 300.05 |
| 10 | 3000+0.05 = 3000.05 |
| 1 | 30000+0.05 = 30000.05 |
| 0.1 | 300000+0.05 = 300000.05 |
Possiamo dire che man mano che n tende a 0 CU tende all'infinito. Graficamente abbiamo che avvicinandosi all'asse verticale il  grafico di CU in funzione di n tende a salire senza limitazioni. Nella realtà n non può avvicinarsi a piacere al valore 0 (si può andare da 1 pezzo prodotto a 0 pezzi prodotti; n non può assumere valori intermedi), ma è comodo usare l'espressione precedente, che sarebbe comunque corretta in astratto, ragionando sulla formula e considerando n come un generico numero reale positivo, senza preoccuparsi del contesto a cui ci riferiamo. Più sinteticamente si usano le espressioni:
grafico di CU in funzione di n tende a salire senza limitazioni. Nella realtà n non può avvicinarsi a piacere al valore 0 (si può andare da 1 pezzo prodotto a 0 pezzi prodotti; n non può assumere valori intermedi), ma è comodo usare l'espressione precedente, che sarebbe comunque corretta in astratto, ragionando sulla formula e considerando n come un generico numero reale positivo, senza preoccuparsi del contesto a cui ci riferiamo. Più sinteticamente si usano le espressioni:
| • per n che tende a 0 30000/n + 0.05 tende all'infinito |
| • il limite di 30000/n + 0.05 per n che tende a 0 è ∞ |
| • 30000/n + 0.05 → ∞ per n → 0 | | • lim 30000/n + 0.05 | = ∞ | | n → 0 |
|
| [stiamo intendendo che n sia positivo, ossia tenda a 0 decrescendo, avvicinandosi a 0 "da destra"; se n fosse negativo, cioè se ci avvicinassimo a 0 "da sinistra", il valore della funzione diminuirebbe invece che salire, e il grafico si avvicinerebbe all'asse verticale scendendo; infatti 30000/n sarebbe negativo] | 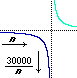 |
Qui si usa la parola "limite" con un salto rispetto al linguaggio comune: con essa non indichiamo più una limitazione, un valore di confine, un punto estremo a cui si può arrivare, ma dicendo che il «limite è infinito» intendiamo dire che la il valore sale oltre ogni "limite".
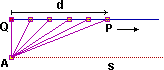 | Nel caso a lato, in cui sono fissati due punti A e Q e una semiretta di origine Q, se indichiamo con P il punto su tale semiretta che dista d da Q, abbiamo che all'allontanarsi di P da Q il segmento AP tende a diventare una semiretta: la semiretta s, di origine A e diretta come la semiretta originale. Possiamo sintetizzare questo fenomeno con l'espressione: |
|
|
Esercizio 1 (e soluzione) Esercizio 2 (e soluzione)
Più avanti ( e
e  ) o in voci successive, quando ne emergerà l'esigenza, verrà precisato meglio l'uso di queste notazioni e di frasi come "si avvicina sempre più a …", "sale senza limitazioni", … (vedremo anche che, tra le situazioni considerate
) o in voci successive, quando ne emergerà l'esigenza, verrà precisato meglio l'uso di queste notazioni e di frasi come "si avvicina sempre più a …", "sale senza limitazioni", … (vedremo anche che, tra le situazioni considerate  sopra, quella della stabilizzazione delle frequenze sperimentali differisce per alcuni aspetti dalle altre). Per consolidare l'idea del concetto di limite vediamo qualche altro esempio, riferito a funzioni a 1 input e 1 output reali.
sopra, quella della stabilizzazione delle frequenze sperimentali differisce per alcuni aspetti dalle altre). Per consolidare l'idea del concetto di limite vediamo qualche altro esempio, riferito a funzioni a 1 input e 1 output reali.
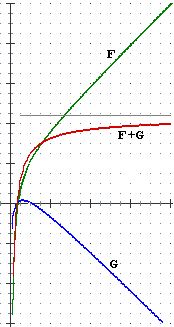
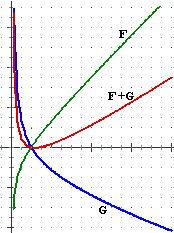
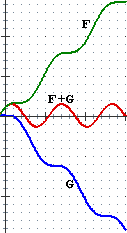
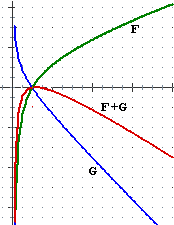
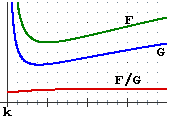
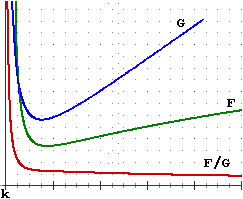
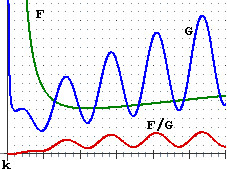
 Nelle figure seguenti i "..." indicano che il grafico prosegue mantenendo un andamento analogo; più precisamente nel caso di F prosegue tendendo a spiaccicarsi sulla retta y=1; nel caso di G prosegue a zig-zag, periodicamente; nel caso di H prosegue a destra e a sinistra spiaccicandosi sulla retta y=–1, in alto e in basso spiaccicandosi sulla retta x=1; nel caso di K prosegue a sinistra spiaccicandosi sull'asse x, a destra continuando a salire, sempre più rapidamente.
Nelle figure seguenti i "..." indicano che il grafico prosegue mantenendo un andamento analogo; più precisamente nel caso di F prosegue tendendo a spiaccicarsi sulla retta y=1; nel caso di G prosegue a zig-zag, periodicamente; nel caso di H prosegue a destra e a sinistra spiaccicandosi sulla retta y=–1, in alto e in basso spiaccicandosi sulla retta x=1; nel caso di K prosegue a sinistra spiaccicandosi sull'asse x, a destra continuando a salire, sempre più rapidamente.
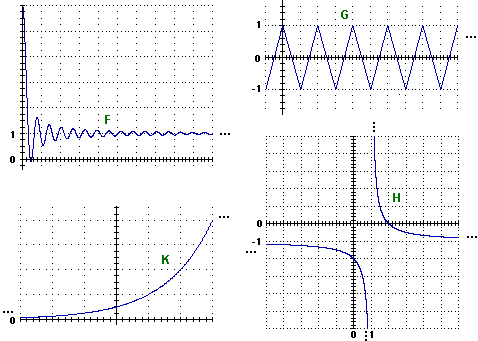
|
|
|
| lim H(x) | = –∞ | x  1 1 |
|
| lim H(x) | = ∞ | x  1 1 |
|
| Le due ultime notazioni stanno a indicare il comportamento limite di H(x) per x che tende a 1 crescendo, ossia provenendo "da sinistra", e decrescendo, ossia "da destra". |
| A loro posto si usano anche le notazioni a fianco, che sono dovute al fatto che nel primo caso x tende a 1 rimanendo 1 "meno" qualcosa e che nell'altro tende a 1 rimanendo 1 "più" qualcosa.
|
|
|
Esercizio 1 (e soluzione)
Esercizio 2 (e soluzione)
 Il grafico a destra illustra un altro esempio di funzione con limiti "da destra" e "da sinistra" diversi. Potrebbe essere il grafico con cui valutare il costo unitario CU settimanale di una piccola gelateria artigianale in funzione del numero x di coni prodotti (supponendo per semplicità che la gelateria produca un solo tipo di coni gelato), nell'ipotesi che i costi incorporati siano di 0.50 euro a cono, che con l'attuale orario di apertura si riescano a produrre e vendere fino a 1800 coni alla settimana e che un'orario di apertura esteso comporterebbe una aggiunta di 81 euro per lo straordinario del dipendente rispetto ai normali costi fissi di 153 euro settimanali: Il grafico a destra illustra un altro esempio di funzione con limiti "da destra" e "da sinistra" diversi. Potrebbe essere il grafico con cui valutare il costo unitario CU settimanale di una piccola gelateria artigianale in funzione del numero x di coni prodotti (supponendo per semplicità che la gelateria produca un solo tipo di coni gelato), nell'ipotesi che i costi incorporati siano di 0.50 euro a cono, che con l'attuale orario di apertura si riescano a produrre e vendere fino a 1800 coni alla settimana e che un'orario di apertura esteso comporterebbe una aggiunta di 81 euro per lo straordinario del dipendente rispetto ai normali costi fissi di 153 euro settimanali:
per x ≤ 1800 CU(x) = 153 / x + 0.50
per x > 1800 CU(x) = 234 / x + 0.50 |
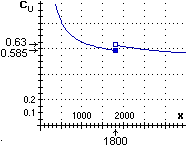 |
In orario ridotto man mano che ci si avvicina, aumentando la produzione, a 1800 coni di produzione il costo unitario tende a 153/1800+0.50 = 0.585 euro: per x → 1800– CU(x) → 0.585.
In orario esteso man mano che ci si avvicina, diminuendo la produzione, a 1800 coni di produzione il costo unitario tende a 234/1800+0.50 = 0.63 euro: per x → 1800+ CU(x) → 0.63.
[Conclusione: se si pensa di non riuscire a vendere molti coni in più non conviene estendere l'orario: per quantità vicine al volume di produzione attualmente raggiungibile il costo unitario sarebbe maggiore]
|
 Alla voce Alla voce
 funzioni polinomiali abbiamo considerato funzioni che hanno limite da destra e da sinistra uguali, come F: x → (x2–2x–3)/(x+1) per x che tende a -1: è una funzione che per x funzioni polinomiali abbiamo considerato funzioni che hanno limite da destra e da sinistra uguali, come F: x → (x2–2x–3)/(x+1) per x che tende a -1: è una funzione che per x 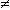 -1 si comporta come x → x-3 e quindi per x che si avvicina a -1 tende ad assumere lo stesso valore che assume tale funzione, ossia -1-3 = -4. -1 si comporta come x → x-3 e quindi per x che si avvicina a -1 tende ad assumere lo stesso valore che assume tale funzione, ossia -1-3 = -4.
In questo caso scrivendo che F(x) → -4 per x → 1 sottointendiamo che i limiti per x → -1+ e per x → -1- coincidono, e sono entrambi uguali a -4.
Per un altro es. prendiamo G: x → (1+x2)1/x. Se ne tracciamo il grafico otteniamo un esito come quello sotto a sinistra. Abbiamo messo un pallino in corrispondenza di x=0 in quanto G(0) non è definito. | 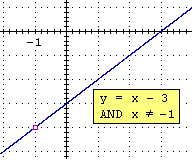 |
 | Dal grafico sembra che lim x → 0G(x) = 1.
La cosa è confermata dallo studio con una calcolatrice del comportamento di G(x) per x → 0+ e per x → 0-: |
| | G(x) = 1.1046221 se x = 0.1
G(x) = 1.0100497 se x = 0.01
G(x) = 1.0010005 se x = 0.001
G(x) = 1.0001000 se x = 0.0001
G(x) = 1.0000100 se x = 0.00001
G(x) = 1.0000010 se x = 0.000001 |
G(x) = 0.90528695 se x = -0.1
G(x) = 0.99005033 se x = -0.01
G(x) = 0.99900050 se x = -0.001
G(x) = 0.99990001 se x = -0.0001
G(x) = 0.99999000 se x = -0.00001
G(x) = 0.99999900 se x = -0.000001 |
In entrambe le direzioni le uscite tendono a stabilizzarsi su 1.
Se definiamo una nuova funzione H ponendo H(x) = G(x) se x 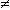 0 e H(0) = 1, riempiamo il "buco", ottenendo una funzione continua in tutto R.
0 e H(0) = 1, riempiamo il "buco", ottenendo una funzione continua in tutto R.
 Usando la terminologia introdotta in questa voce, possiamo riesprimere la definizione di
Usando la terminologia introdotta in questa voce, possiamo riesprimere la definizione di  funzione continua in un intervallo [a,b] dicendo che una funzione F è tale se al tendere a 0 della distanza tra due input presi comunque in [a,b] anche la distanza tra i loro output tende a 0.
È quindi ovvio che se F è continua in un intervallo [a,b] e p è in tale intervallo, allora lim x → p F(x) = F(p).
funzione continua in un intervallo [a,b] dicendo che una funzione F è tale se al tendere a 0 della distanza tra due input presi comunque in [a,b] anche la distanza tra i loro output tende a 0.
È quindi ovvio che se F è continua in un intervallo [a,b] e p è in tale intervallo, allora lim x → p F(x) = F(p).
I punti del dominio di una funzione in cui ciò non accade sono detti punti di discontinuità della funzione.
Se una funzione ha per dominio un insieme che non è un  intervallo chiuso e limitato, cioè che non è
del tipo [a,b], si dice che è continua nel suo dominio se lo è in ciascun intervallo chiuso e limitato contenuto in esso. Ad es. x → 1/x è continua nel suo dominio. In questo caso 0 non è un punto di discontinuità in quanto non appartiene al dominio.
intervallo chiuso e limitato, cioè che non è
del tipo [a,b], si dice che è continua nel suo dominio se lo è in ciascun intervallo chiuso e limitato contenuto in esso. Ad es. x → 1/x è continua nel suo dominio. In questo caso 0 non è un punto di discontinuità in quanto non appartiene al dominio.
Si noti che se considerassi l'intervallo aperto a sinistra (0,2] non avrei che all'infittire degli input gli output di x → 1/x si infittiscono in tutto l'intervallo: nei pressi dell'asse y potrei sempre trovare dei punti del grafico distanti tra loro quanto voglio; infatti 1/x → ∞ per x → 0+. Ma in ogni intervallo [ε,2], per quanto piccolo sia il numero positivo ε, questo infittimento si verifica.
Tracciando i punti con un computer si arriva comunque a un infittimento in quanto sullo schermo compare solo una porzione limitata del piano cartesiano e i punti del grafico più vicini all'asse y non vengono visualizzati.
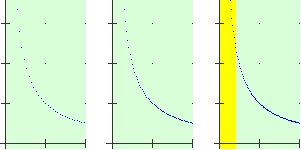
Il tracciamento di un grafico con un computer, se non si riflette su ciò su ciò che si sta facendo e non si tiene conto dei limiti del software che si impiega, a volte può suggerire delle considerazioni sbagliate. Ad esempio, come nel caso dei grafici "bucati" considerati sopra  , si può ottenere un insieme di pixel tutti attaccati, senza rendersi conto della presenza di un punto in cui la funzione non è definita. Oppure nel caso di x → 1/x, sempre come effetto del "salto" di un buco da parte del programma che si impiega, si potrebbe ottenere un grafico come quello sotto a sinistra (in cui vengono congiunti punti appartenenti a rami di curva distinti). Vi possono essere anche casi in cui, per effetto di semplificazioni o di altre manipolazioni algebriche che il programma esegue automaticamente, il grafico venga tracciato anche per interi intervalli in cui la funzione non è definita. Poi vi sono funzioni che non sono alla portata del computer, come la funzione F così definita:
, si può ottenere un insieme di pixel tutti attaccati, senza rendersi conto della presenza di un punto in cui la funzione non è definita. Oppure nel caso di x → 1/x, sempre come effetto del "salto" di un buco da parte del programma che si impiega, si potrebbe ottenere un grafico come quello sotto a sinistra (in cui vengono congiunti punti appartenenti a rami di curva distinti). Vi possono essere anche casi in cui, per effetto di semplificazioni o di altre manipolazioni algebriche che il programma esegue automaticamente, il grafico venga tracciato anche per interi intervalli in cui la funzione non è definita. Poi vi sono funzioni che non sono alla portata del computer, come la funzione F così definita:
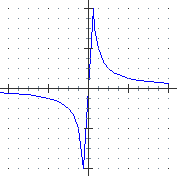 |  | x → 1 se x è razionale,
x → 2 se x è irrazionale.
Se cercassimo di tracciare a mano il suo grafico dovremmo fare una rappresentazione come quella qui a lato: due "rette" orizzontali che, in realtà, sono piene di infiniti buchi. Si tratta di buchi che però non si possono "vedere": presi comunque due input h e k esitono tra di essi sia numeri razionali che numeri irrazionali (ad es. tra 3.23 e 3.24 ci stanno sia il razionale 3.23333… che l'irrazionale 3.2313113111311113…); sono buchi di dimensione nulla. Il computer non riuscirebbe a percepire nulla di tutto ciò perché nella elaborazione non può valutare se i valori che x man mano assume sono razionali o no (nelle elaborazioni numeriche approssima i numeri in forma limitata: per esso diventano tutti numeri razionali); per altro non esiste alcun algoritmo che, preso in input un qualunque numero reale, sia in ogni caso capace di stabilire se esso sia irrazionale o no. |
Nota.
Invece che definire la continuità in un intervallo, si sarebbe potuto definire una funzione F come continua in un punto p del suo dominio se lim x → p F(x) = F(p).
Si sarebbe poi definita F continua in un intervallo se è continua in tutti i suoi punti. Non sarebbe stato, però, facile dimostrare la proprietà, fondamentale, che se una funzione è continua in un intervallo [a,b] allora si ha che in esso gli output infittiscono all'infittirsi degli input (chi segue tale approccio usa in genere il termine "uniforme continuità" per descrivere questa proprietà, che noi, invece, abbiamo assunto come definizione).
Esercizio 1 (e soluzione)
Esercizio 2 (e soluzione)
 È utile mettere a punto alcune proprietà che ci facilitino nel calcolo dei limiti di funzioni ottenute componendo altre funzioni di cui ci sia già noto il comportamento. È utile mettere a punto alcune proprietà che ci facilitino nel calcolo dei limiti di funzioni ottenute componendo altre funzioni di cui ci sia già noto il comportamento. |
È ovvio che se per x → α (dove con α qui intendiamo un numero o ∞ o -∞) F(x) → L, allora se G(x) = F(x)+h si ha che G(x) → L+h (il suo grafico è quello di F traslato verticalmente di h). Ne abbiamo già visto  esempi. esempi.
|
Se per x → α ho sia che F(x) → 0 sia che G(x) → 0, posso concludere che F(x)+G(x) → 0.
La cosa è intutivamente evidente.
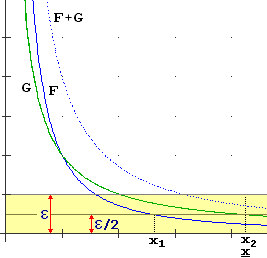
Comunque a destra è illustrata una spiegazione più formale per il caso in cui x → ∞:
• voglio far vedere che "aumentando il valore dell'input x posso far sì che l'output F(x)+G(x) si stabilizzi vicino quanto voglio a 0";
posso precisare questa condizione così:
comunque fissi un numero positivo ε
("epsilon", lettera greca che corrisponde alla nostra "e" breve)
posso trovare un valore x tale che per ogni input ad esso superiore l'output disti da 0 meno di ε.
• siccome F(x) e G(x) tendono entrambi a 0, posso trovare un input oltre il quale entrambi si stabilizzino a una distanza da 0 inferiore ad ε/2
(se per x > x1 F(x) dista da 0 meno di ε/2 e per x > x2 G(x) dista da 0 meno di ε/2, basta che prenda x pari al massimo tra x1 e x2, ossia x2 nel caso illustrato);
• abbiamo, dunque, che per x > x F(x)+G(x) dista da 0 meno di ε/2+ε/2 = ε.
|  |
Più in generale, se per x → α F(x) → L e G(x) → M, allora F(x)+G(x) → L+M. Infatti F(x)-L e G(x)-M tendono a 0, per cui F(x)+G(x)-(L+M), che equivale a (F(x)-L)+(G(x)-M), tende a 0, ossia F(x)+G(x) tende a L+M.
In breve, se per x → α F(x) e G(x) hanno limite finito:
lim x → α (F(x)+G(x)) = lim x → α F(x) + lim x → α G(x).
|
|
Analogamente valgono le seguenti proprietà, nel caso in cui tutti i limiti siano considerati per x che tende allo stesso α: |
– se F(x) → L allora –F(x) → –L;
– se F(x) → L e G(x) → M allora F(x)·G(x) → L·M;
– se F(x) → L e G(x) → M diverso da 0, allora F(x)/G(x) → L/M;
– se F(x) → L e G(x) → M allora F(x)G(x) → LM (L e M non devono essere entrambi nulli, in quanto 00 non è definito);
– se F(x) → L e G(x) → M e (almeno da un certo punto in poi, procedendo verso α) F(x) ≤ G(x), allora L≤M.
Si noti che anche se F(x) < G(x) può essere che L=M (si veda il caso illustrato nella figura precedente).
Si noti inoltre che, quando α non è infinito, non ci interessa che F(x)≤G(x) sia verificata anche per x = α: vogliamo infatti studiare il comportamento "al limite", e valutare eventualmente (come nell'esempio di CU(x) per x→1800+ visto  sopra) se questo è diverso dal valore che la funzione assume in α.
sopra) se questo è diverso dal valore che la funzione assume in α.
Possiamo sintetizzare quanto osservato dicendo che il passaggio al limite conserva somme, prodotti, quozienti e relazioni d'ordine (in senso lato: ≥ e ≤, non necessariamente > e <).
Un esempio (per la conservazione di "·" e "+"):
lim x→∞ ((3+5/x) (2+7/x) / (15-1/x) + 3/x)
per x → ∞ 3+5/x → 3, 2+7/x → 2, 15-1/x → 15, 3/x → 0,
quindi l'intero termine tende a 3 · 2 / 15 + 0, ossia a 2/5.
Un altro esempio (per la conservazione di "≤"):
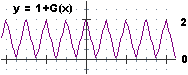
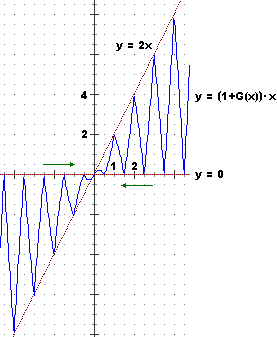
lim x→0 ((1+G(x))·x) dove G è la funzione con grafico "dentato" considerata  poco sopra. poco sopra.
0 ≤ 1+G(x) ≤ 2, quindi, moltiplicando per x [ disequazioni]: disequazioni]:
• per x>0, 0 = 0·x ≤ (1+G(x))·x ≤ 2·x, quindi per x → 0+,
poiché 0 → 0 e 2x → 0, anche (1+G(x))·x → 0;
• per x<0, 2·x ≤ (1+G(x))·x ≤ 0·x = 0, quindi per x → 0-,
poiché 0 → 0 e 2x → 0, anche (1+G(x))·x → 0.
Dunque per x → 0 (sia da destra che da sinistra) (1+G(x))·x → 0.
| 
 |
Nota. Se F(x) ≤ H(x) ≤ G(x) e
per x → α F(x) e G(x) hanno lo stesso limite, allora ad esso,
per x → α, tende anche H(x). Questa proprietà,
che è una facile conseguenza del fatto che il passaggio al limite conserva in senso lato
le relazioni d'ordine, è, in Italia, spesso chiamata teorema dei carabinieri
in quanto un prigioniero che sta tra due carabinieri va nello stesso posto dove vanno
essi; in altri paesi è chiamata, per motivi simili, teorema del sandwich.
Esercizio (e soluzione)
 Con qualche semplice ragionamento intuitivo si può capire come estendere
Con qualche semplice ragionamento intuitivo si può capire come estendere  queste proprietà ai casi in cui al posto di L o di M mettiamo ∞ o -∞. Facciamo qui solo alcuni esempi:
queste proprietà ai casi in cui al posto di L o di M mettiamo ∞ o -∞. Facciamo qui solo alcuni esempi:
– se F(x) → L e G(x) → ∞, G(x) sale oltre ogni limitazione e, dato che F(x) tende a stabilizzarsi su L, altrettanto accade a F(x)+G(x): F(x)+G(x) → ∞ ["in breve": L+∞ = ∞]
– se F(x) → L e G(x) → ∞, F(x) tende a stabilizzarsi su L e G(x) sale oltre ogni limitazione, quindi F(x)/G(x) rimpicciolisce tendendo a 0: F(x)/G(x) → 0 ["in breve": L/∞ = 0]
– se F(x) → ∞ e G(x) → ∞, dato che sia G(x) che F(x) tendono a salire oltre ogni limitazione, lo stesso accade, a maggior ragione, per F(x)+G(x): F(x)+G(x) → ∞ ["in breve": ∞+∞ = ∞]
– se F(x) → ∞ e G(x) → -∞, F(x) sale oltre ogni limitazione mentre G(x) scende oltre ogni limitazione, ma se non sappiamo che uno dei due prevale, senza altre informazioni non possiamo concludere nulla sul comportamento di F(x)+G(x) per x → α ["in breve": ∞–∞ = ?]. Sotto sono illustrati i vari casi (per α = ∞).
Facciamo ancora tre esempi:
– se F(x) → L > 0 e G(x) → 0- (tende a 0 "da sotto", ossia si avvicina a 0 avendo valore negativo), F(x)/G(x) tenderà ad avere un comportamento che assomiglia a  quello di L/x per x → 0-, ossia F(x)/G(x) → -∞ ["in breve", se L>0: L/0- = -∞; analogamente: L/0+ = ∞]
quello di L/x per x → 0-, ossia F(x)/G(x) → -∞ ["in breve", se L>0: L/0- = -∞; analogamente: L/0+ = ∞]
– se F(x) → ∞ e G(x) → 0, e non sappiamo che prevale l'effetto ingranditivo della moltiplicazione per F(x) o quello riduttivo della moltiplicazione per G(x), non possiamo concludere nulla sul comportamento di F(x)·G(x) per x → α ["in breve": ∞·0 = ?]
– se F(x) → ∞ e G(x) → ∞, e non sappiamo se uno dei due comportamenti tende a prevalere, non possiamo concludere nulla sul comportamento di F(x)/G(x) per x → α; questo caso equivale al precedente, infatti F(x)/G(x) = F(x)·(1/G(x)) e 1/G(x) → 0 se G(x) → ∞ ["in breve": ∞/∞ = ?].
Qualche grafico esemplificativo:
 Se cerco di capire come si comporta 101/x per x → ∞ è naturale ragionare in questo modo:
Se cerco di capire come si comporta 101/x per x → ∞ è naturale ragionare in questo modo:
– per x → ∞ so che 1/x → 0;
– quindi 101/x si comporta come 10u per u → 0;
– limu → 010u = 100 = 1 in quanto x → 10x è continua.
Analogamente di fronte allo studio di 101/x per x → 0- ragiono così:
– per x → 0- so che 1/x → -∞;
– quindi 101/x si comporta come 10u per u → -∞;
– limu → -∞10u = 0. | 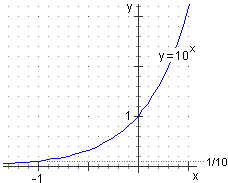 |
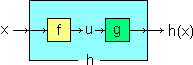 |
Più in generale se devo studiare h(x) per x → α e h posso vederla come composizione di f e g, ossia h(x) = g(f(x)), posso procedere così:
– penso h(x) come g(u) con u=f(x);
– guardo come si comporta f(x) per x → α;
– se f(x) → β mi riconduco allo studio di g(u) per u → β. |
Se g è continua si può sempre procedere in questo modo.
Ci sono dei rari casi "patologici" in cui il procedimento non vale. Ecco un esempio:
– siano f e g le funzioni rappresentate graficamente a fianco;
– per x → 1 f(x) → 0.5;
– per u → 0.5 g(u) → 1.5;
– mentre per x → 1 g(f(x)) → 1;
infatti per x vicino a 1 f(x)=0.5 e g(0.5)=1. | 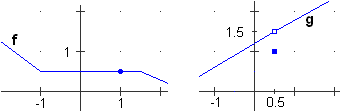 |
 |
Fenomeni di questo genere si possono verificare solo se
• g non è continua e
• f è costante vicino al valore x a cui si fa tendere l'input,
come nel caso ora visto, o, più in generale, per quanto ci si avvicini ad x,
assume in più punti lo stesso valore che ha in x,
come accade alla funzione rappresentata a lato:
per x → 1 f(x) → 0.5
mentre g(f(x)) non solo non ha lo stesso limite di g(u) per u → 0.5,
ma non ha neanche limite: comunque mi avvicino a 1 vi sono degli x per cui f(x)=0.5,
e g(f(x)) vale 1,
mentre negli altri punti f(x) si avvicina a 0.5 senza assumerne il valore per cui g(f(x)) si avvicina ad
1.
|
 Quando si ragiona sul comportamento limite di funzioni ottenute componendo altre funzioni bisogna stare attenti a non farsi ingannare dall'intuizione, in particolare nei casi in cui si ha a che fare con una funzione che tende a 1 elevata a una funzione che tende all'infinito:
Quando si ragiona sul comportamento limite di funzioni ottenute componendo altre funzioni bisogna stare attenti a non farsi ingannare dall'intuizione, in particolare nei casi in cui si ha a che fare con una funzione che tende a 1 elevata a una funzione che tende all'infinito: |
se per x → α F(x) → 1 e G(x) → ∞ uno potrebbe pensare che F(x)G(x) → 1 in quanto F(x) tende a comportarsi come 1 e 1 elevato a un qualsiasi esponente è uguale e 1.
Si tratta di un ragionamento ingannevole in quanto con esso differiamo nel tempo la considerazione di F e quella di G mentre esse agiscono contemporaneamente: ad es. se F(x)→1+ l'elevamento a una potenza positiva di F(x) ne accresce il valore, per cui il comportamento complessivo di F(x)G(x) dipende se prevale la tendenza riduttrice dovuta all'abbassamento della base F(x) o quella ingranditrice dovuta all'aumento dell'esponente G(x).
A lato sono illustrati alcuni casi, in due dei quali il limite non è 1.
Vedremo più avanti (alla voce  Funz. esponenziale e logaritmo) un "trucco" utile per studiare limiti di questo tipo (esercizio, soluzione). Funz. esponenziale e logaritmo) un "trucco" utile per studiare limiti di questo tipo (esercizio, soluzione). | 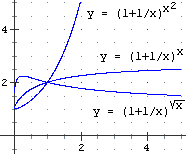 |
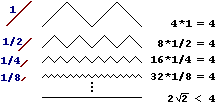 |  Affidandosi in modo disinvolto all'intuizione ci si può ingannare non solo nel "calcolo" dei limiti, come abbiamo appena visto, ma anche quando si usa il concetto di limite per affrontare particolari situazioni, come ad es. di misurazione, come quelle accennate
Affidandosi in modo disinvolto all'intuizione ci si può ingannare non solo nel "calcolo" dei limiti, come abbiamo appena visto, ma anche quando si usa il concetto di limite per affrontare particolari situazioni, come ad es. di misurazione, come quelle accennate  sopra. La figura a lato esemplifica ciò in un caso in cui è evidente che si è commesso qualche errore; in altri casi la cosa non è così chiara. sopra. La figura a lato esemplifica ciò in un caso in cui è evidente che si è commesso qualche errore; in altri casi la cosa non è così chiara. |
| Siamo di fronte a una successione di spezzate di uguali estremi di cui sono raffigurati i primi 4 elementi (la prima spezzata ha 4 segmenti, la seconda 8, la terza 16, la quarta 32, …); le spezzate man mano meglio approssimano il segmento che congiunge i due estremi. Potremmo pensare che la lunghezza delle spezzate tenda alla lunghezza del segmento. Ma il segmento è lungo 2√2 (il doppio della diagonale di un quadrato di lato 1), mentre le spezzate, per quanto si appiattiscano, si mantengono sempre lunghe 4. |
| Esercizio (e soluzione) |
 Definizioni.
Sopra [
Definizioni.
Sopra [ ] abbiamo visto come può essere precisata la condizione limx → ∞f(x) = L (f funzione a input e output reali, L numero reale); vi era anche un
] abbiamo visto come può essere precisata la condizione limx → ∞f(x) = L (f funzione a input e output reali, L numero reale); vi era anche un  esercizio che ti faceva riflettere come precisare in modo analogo altre condizione di limite. Comunque:
esercizio che ti faceva riflettere come precisare in modo analogo altre condizione di limite. Comunque:
lim x → – ∞ f(x) = L può essere definita equivalente a:
comunque fissi ε
positivo posso trovare x tale che per ogni x
minore di x f(x)
disti da L
meno di ε.
lim x → ∞ f(x) = ∞
(che corrisponde all'idea che f(x) possa aumentare oltre ogni limite facendo crescere opportunamente x)
si può definire equivalente a:
comunque fissi K
posso trovare x tale che per ogni x
maggiore di x f(x)
sia maggiore di K.
lim x → ∞ f(x) = -∞
si può definire equivalente a
comunque fissi K
posso trovare x tale che per ogni x
maggiore di x f(x)
sia minore di K.
lim x → p f(x) = ∞ (che corrisponde all'idea che
f(x) possa aumentare oltre ogni limite facendo avvicinare opportunamente x a p)
si può definire equivalente a
comunque fissi K
posso trovare δ
positivo tale che per ogni x
diverso da p
e distante
da p
meno di δ
f(x)
sia maggiore di K.
lim x → p+ f(x) = L
si può definire equivalente a
comunque fissi ε
positivo posso trovare δ
positivo tale che per ogni x
maggiore di p
e distante
da p
meno di δ
f(x)
sia maggiore di K.
ecc.
 Diremo che lim x → α f(x) non esiste nei casi in cui non esista L numero reale tale che
limx → αf(x) = L e non si abbia né limx → αf(x) = ∞ né limx → αf(x) = -∞.
Diremo che lim x → α f(x) non esiste nei casi in cui non esista L numero reale tale che
limx → αf(x) = L e non si abbia né limx → αf(x) = ∞ né limx → αf(x) = -∞.
Queste condizioni di "non esistenza" del limite includono anche quelle in cui non
abbia senso far tendere x
ad α
stando nel dominio di f, ossia:
nel caso in cui α sia ∞, quando il dominio non è illimitato superiormente;
nel caso in cui α sia
-∞, quando il dominio non è illimitato inferiormente;
e nel caso in cui α sia
un numero reale, quando α non è un punto interno o agli estremi di un intervallo in cui F sia definita o, più in generale, quando α è un punto
isolato per il dominio di F,
ossia quando si può trovare δ positivo tale che non vi sia alcun punto x del dominio che sia diverso da α e disti da α meno di δ
(questa non è altro che una possibile formalizzazione dell'idea del
non potersi avvicinare quanto si vuole ad α stando nel dominio di F).
Ad
es. se P(N) è il perimetro un poligono regolare di N lati inscritto in un cerchio di raggio 1,
possiamo cercare di calcolare
limN → ∞P(N) in quanto
P(N) è definito per ogni N intero positivo,
e quindi il suo dominio è
illimitato superiormente (e sappiamo che il limite è 2π).
Non
ha invece senso cercar di calcolare
limN → -∞P(N) o
limN → 0P(N)
in quanto da una parte il domino non è illimitato inferiormente e, dall'altra, 0 è un punto isolato per il dominio; la stessa cosa si potrebbe dire per il limite per N → K per un qualunque altro intero K.
 Considerazioni analoghe valgono per tutte le
Considerazioni analoghe valgono per tutte le  successioni,
cioè per tutte le funzioni che hanno per dominio l'insieme dei numeri naturali
(o quello dei numeri interi positivi):
per una successione N → A(N) può esistere il limite per N → ∞ ma sicuramente non possono
essere definiti il limiti per N → -∞ e quello per N → p per alcun numero p.
Per questo motivo quando si parla di limite di una successione A(N)
si sottointende che sia il limite per N → ∞. Quando questo limite esiste ed è finito,
ossia è un numero L, si dice che la successione è convergente, e converge a L. Quando una successione non converge, si dice che diverge, ed eventualmente che diverge a ∞ [-∞] se ha limite e questo è ∞ [-∞].
successioni,
cioè per tutte le funzioni che hanno per dominio l'insieme dei numeri naturali
(o quello dei numeri interi positivi):
per una successione N → A(N) può esistere il limite per N → ∞ ma sicuramente non possono
essere definiti il limiti per N → -∞ e quello per N → p per alcun numero p.
Per questo motivo quando si parla di limite di una successione A(N)
si sottointende che sia il limite per N → ∞. Quando questo limite esiste ed è finito,
ossia è un numero L, si dice che la successione è convergente, e converge a L. Quando una successione non converge, si dice che diverge, ed eventualmente che diverge a ∞ [-∞] se ha limite e questo è ∞ [-∞].
Quando si studia sperimentalmente il limite di una funzione,
come nel caso della funzione G considerata in un  esempio precedente, in pratica si esamina il comportamento della funzione non su tutti gli input, ma su una successione di input.
Si studia, quindi, il limite di una successione di valori della funzione,
da cui si cerca di dedurre il limite della funzione stessa.
Gli esercizi seguenti illustrano altri esempi e (il secondo) le attenzioni
da prestare nel trasferire le congetture fatte su queste successioni al comportamento
complessivo della funzione (il fatto che per un po' di x(n) tendenti ad k
f(x(n)) converga
per n → ∞ non assicura che esista il limite di
f(x) per x che tende a k).
esempio precedente, in pratica si esamina il comportamento della funzione non su tutti gli input, ma su una successione di input.
Si studia, quindi, il limite di una successione di valori della funzione,
da cui si cerca di dedurre il limite della funzione stessa.
Gli esercizi seguenti illustrano altri esempi e (il secondo) le attenzioni
da prestare nel trasferire le congetture fatte su queste successioni al comportamento
complessivo della funzione (il fatto che per un po' di x(n) tendenti ad k
f(x(n)) converga
per n → ∞ non assicura che esista il limite di
f(x) per x che tende a k).
Esercizio 1 (e soluzione) Esercizio 2 (e soluzione)
 Nota. Alcuni autori usano "+∞" al posto di "∞" in quanto indicano con limx → α f(x) = +∞ ciò che noi abbiamo indicato con limx → α f(x) = ∞ mentre considerano questa scrittura, ossia limx → α f(x) = ∞, come equivalente a limx → α |f(x)| = +∞. Da tali autori "∞" è chiamato infinito senza segno. Si tratta di una convenzione che può essere utile in alcuni specifici settori avanzati della matematica.
Nota. Alcuni autori usano "+∞" al posto di "∞" in quanto indicano con limx → α f(x) = +∞ ciò che noi abbiamo indicato con limx → α f(x) = ∞ mentre considerano questa scrittura, ossia limx → α f(x) = ∞, come equivalente a limx → α |f(x)| = +∞. Da tali autori "∞" è chiamato infinito senza segno. Si tratta di una convenzione che può essere utile in alcuni specifici settori avanzati della matematica.
Esercizi:  [fino all'es. 6.8]
[fino all'es. 6.8]
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che:
La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che: "limiti di un modello": si intende indicare che esso deve essere usato tenendo conto delle semplificazioni operate, stando attenti a non estendere troppo le conclusioni basate sull'analisi di esso.
"limiti di un modello": si intende indicare che esso deve essere usato tenendo conto delle semplificazioni operate, stando attenti a non estendere troppo le conclusioni basate sull'analisi di esso.







 1
1 1
1
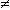 -1 si comporta come
-1 si comporta come