Pendenze e curve di livello
 Alcune cartine, come quella sotto a sinistra, presentano l'indicazione sia
delle curve di livello, sia (mediante "angolini" del tipo:
">>>") della
Alcune cartine, come quella sotto a sinistra, presentano l'indicazione sia
delle curve di livello, sia (mediante "angolini" del tipo:
">>>") della  pendenza dei tratti di strada più
ripidi.
Ciò consente di farsi un'idea tridimensionale del territorio
rappresentato.
pendenza dei tratti di strada più
ripidi.
Ciò consente di farsi un'idea tridimensionale del territorio
rappresentato.
Una curva di livello è
una linea costituita da punti che rappresentano posizioni della
superficie terrestre che sono alla stessa quota sul livello del mare
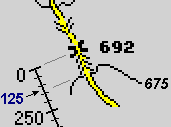
(altitudine). Sopra a destra è raffigurato il plastico che si può ottenere sulla base delle curve di livello della cartina a sinistra.
La figura sopra al plastico consente di verificare la pendenza indicata dai tre "angolini" (superiore al 12%): il tratto di strada che va dall'altitudine di 675 m al passo, a 692 m, è lungo circa 125 m, il dislivello è 17 m, quindi la pendenza è circa 17/125 = 0.136 = [approssimando] 0.14 = 14%.
Al posto di "curva di livello" si usa anche l'espressione
isoipsa (dal greco isos = uguale e hypsos = alto).
Vedi in fondo alla pagina un'immagine tratta da un libro di geografia.
Se le curve sono tracciate in
corrispondenza di quote che differiscono l'una dall'altra dello
stesso dislivello, l'infittirsi delle curve indica un aumento della
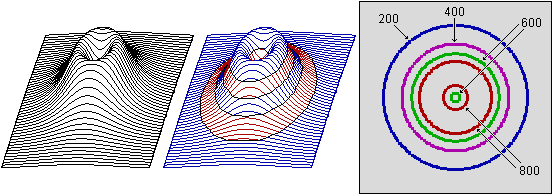
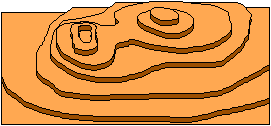
pendenza: nel caso della superficie "ideale" sotto
riprodotta a sinistra (al centro vi è la superficie è "affettatata" alle altituidini di 200 m, 400 m, ...) anche solo osservando le curve di livello, a destra, si capisce che
man mano che si sale lungo il pendio la pendenza aumenta, fino a
quando ci si avvicina al "cratere"; a questo punto la
pendenza comincia a ridursi e, infine, cambia segno (si passa a una
curva di livello più bassa): si comincia a scendere dentro al
cratere.
 Per trovare l'inclinazione di
una strada nota la pendenza [rapporto tra dislivello
superato e corrispondente avanzamento in orizzontale]
si può ricorrere a metodi grafici. Ad esempio, se la pendenza è del 14%,
basta tracciare con riga e squadra un segmento orizzontale lungo 100 mm
(=10 cm) e uno verticale con un estremo in comune con esso lungo
14 mm e, congiunti gli altri estremi, misurare l'inclinazione del
nuovo segmento con un goniometro [in questo caso di ottiene 8°]:
Per trovare l'inclinazione di
una strada nota la pendenza [rapporto tra dislivello
superato e corrispondente avanzamento in orizzontale]
si può ricorrere a metodi grafici. Ad esempio, se la pendenza è del 14%,
basta tracciare con riga e squadra un segmento orizzontale lungo 100 mm
(=10 cm) e uno verticale con un estremo in comune con esso lungo
14 mm e, congiunti gli altri estremi, misurare l'inclinazione del
nuovo segmento con un goniometro [in questo caso di ottiene 8°]:
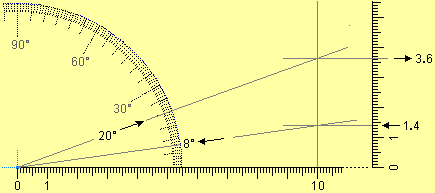
La
figura illustra anche come, viceversa, data l'inclinazione (20°) si può
ricavare la pendenza (36%).
Esercizi: testo1 e soluzione, testo2 e soluzione, testo3 e soluzione, testo4 e soluzione, testo5 e soluzione, testo6 e soluzione.
Un'immagine tratta da un libro di geografia:
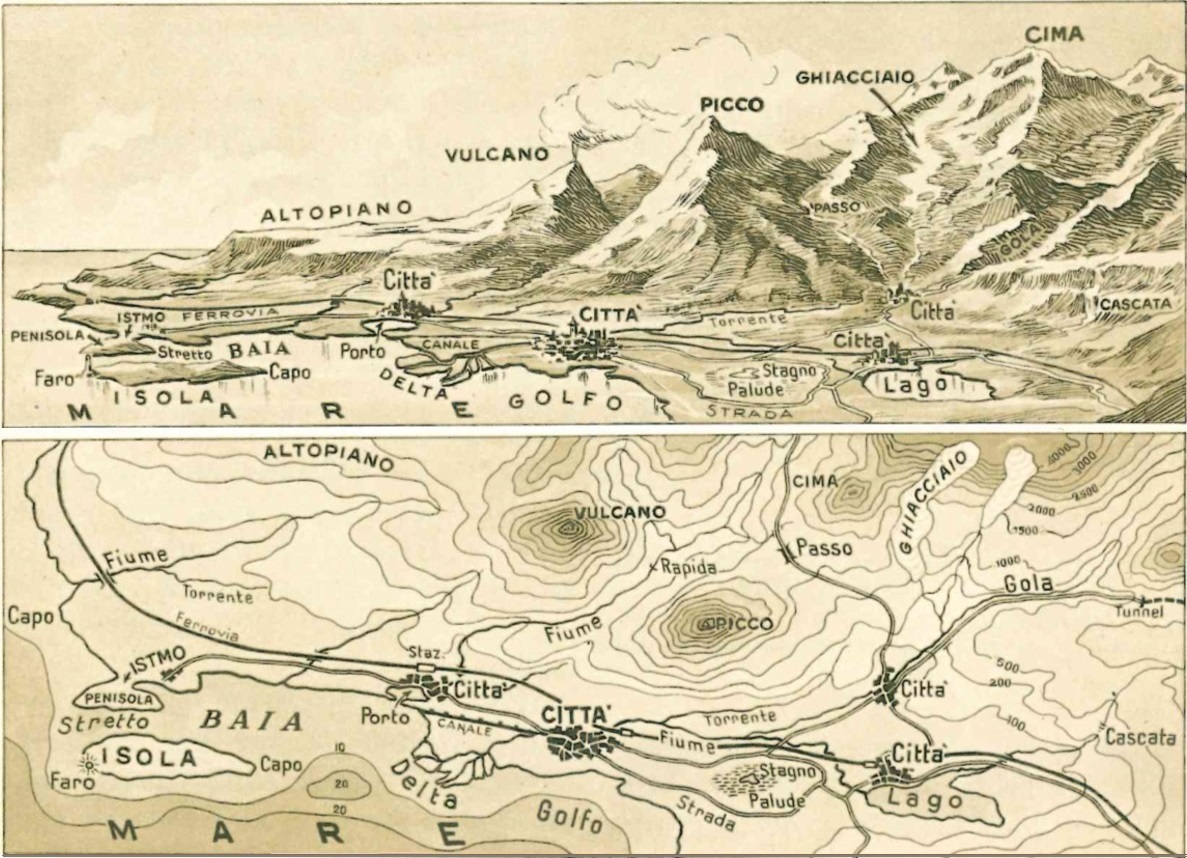
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Alcune cartine, come quella sotto a sinistra, presentano l'indicazione sia
delle curve di livello, sia (mediante "angolini" del tipo:
">>>") della
Alcune cartine, come quella sotto a sinistra, presentano l'indicazione sia
delle curve di livello, sia (mediante "angolini" del tipo:
">>>") della  pendenza dei tratti di strada più
ripidi.
Ciò consente di farsi un'idea tridimensionale del territorio
rappresentato.
pendenza dei tratti di strada più
ripidi.
Ciò consente di farsi un'idea tridimensionale del territorio
rappresentato.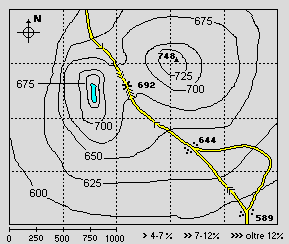


 di una CT
si può calcolare direttamente la pendenza associata a una
certa inclinazione (20
di una CT
si può calcolare direttamente la pendenza associata a una
certa inclinazione (20 
 24
24 



