Introduzione
Introduzione
La programmazione lineare (in simboli, PL o LP) serve per determinare l'allocazione (cioè
la ripartizione e assegnazione) ottimale di risorse,
disponibili in quantità limitata, per ottimizzare il raggiungimento di un obiettivo prestabilito
(in condizioni di certezza, ossia in assenza di valutazioni casuali).
Tra i problemi risolubili con le tecniche della programmazione lineare
vi sono problemi di natura economica, problemi relativi alla distribuzione di risorse, problemi
di trasporto, …
Possiamo ricorrere alla seguente schematizzazione:
| Modello matematico: | { |
Ottimizzare funzione obiettivo (x → f(x), x vettore) Vincoli di segno Vincoli tecnici: eguaglianze o diseguaglianze deboli |
dove tutte le funzioni presenti nel modello sono lineari.
Vedremo come affrontare problemi di programmazione lineare con tre strategie risolutive, che illustreremo a partire da alcuni esempi:
Metodo grafico Metodo algebrico Metodo del simplesso
Vedremo, comunque, come, capito in che modo impostare un problema di programmazione lineare, la sua soluzione sia facilmente affrontabile usando del software, ad esempio R: in analogia a quanto osservato in molte altre situazioni, la difficoltà consiste, essenzialmente, nella matematizzazzione del problema.
 Problemi di PL in due variabili – metodo grafico
Problemi di PL in due variabili – metodo grafico
Problema 1
Sia U l'unità di misura monetaria in vigore. Un'industria produce due prodotti A e B e utilizza due macchinari P e Q. Per ogni unità di A sono necessarie 1 ora di P e 3 ore di Q, per ogni unità di B sono necessarie 2 ore di P e 2 ore di Q. Inoltre A non può essere prodotto in più di 18 pezzi settimanali, la macchina P non può lavorare per più di 40 ore alla settimana, mentre B per non più di 60. Determinare qual è la combinazione produttiva più conveniente, sapendo che ogni unità di A viene venduta a 16000 U e ogni unità di B a 10000 U, nell'ipotesi che ogni quantità prodotta sia venduta.
Schema risolutivo
| A | B | Ore disponibili |
x = quantità di A y = quantità di B z = funzione obiettivo = ricavo | |
| P | 1 | 2 | 40 | |
| Q | 3 | 2 | 60 |
Modello matematico
| max | z = 16000 x + 10000 y | |
| x + 2y ≤ 40 | vincolo n°1 | |
| 3x + 2y ≤ 60 | vincolo n°2 | |
| 0 ≤ x ≤ 18 | vincoli n°3 - n°4 | |
| 0 ≤ y | vincolo n°5 |
In generale un problema di questo tipo può essere schematizzato così:
{z = m x + ny, a x + by ≥ c, …, d x + e y ≥ f, …, x ≥ 0, y ≥ 0}
Passi per determinare la soluzione
• Si rappresenta graficamente il sistema dei vincoli nel piano ottenendo la regione delle soluzioni ammissibili (o dominio dei vincoli). Se l'insieme non è vuoto, tale area può essere rappresentata da un poligono, o da una poligonale illimitata, che possono eventualmente ridursi ad una semiretta, ad un segmento o ad un punto.
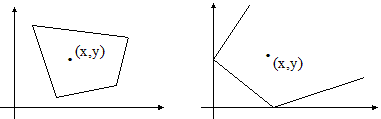
Ogni coppia (x, y) appartenente al dominio dei vincoli si dice soluzione ammissibile e tra queste si cercherà la soluzione ottima.
•
Si rappresentano le linee di livello della funzione obiettivo (rette, in quanto la f.o. è un piano nello spazio).
Si rappresenta la linea di livello corrispondente a z = 0 (retta guida), che divide il piano in due parti in una delle quali z > 0
e nell'altra z < 0.
Il semipiano in cui z > 0 può essere facilmente individuato in quanto è quello che contiene il punto
(m,n) (f.o. z = m x + n y). Infatti il valore assunto da z in (m,n) è m m + n n = m2 + n2. Unendo l'origine O con il punto (m,n)
e disegnando la freccia avente verso da O a (m,n) si individua il semipiano in cui z > 0. Questa freccia
risulta sempre perpendicolare al piano z = mx + ny; essa indica il verso di crescita della funzione obiettivo z = mx + ny.
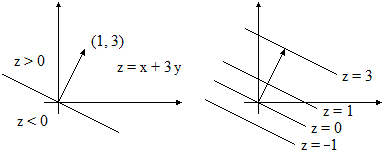
• Dall'andamento delle linee di livello nel dominio si deduce se la funzione ammette massimo o minimo.
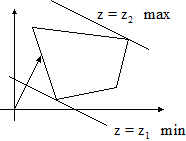
Esempi di regioni ammissibili
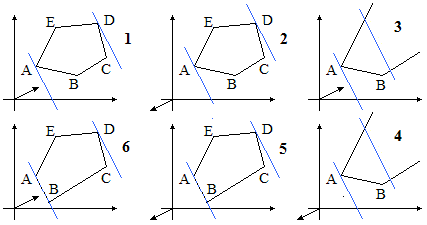
Osservazione
In un problema di programmazione lineare se l'insieme delle soluzioni ammissibili è un poligono chiuso,
allora è un poligono chiuso convesso.
Teorema (Weierstrass + teo. fondamentale progr. lin.)
Se l'insieme delle soluzioni ammissibili è un poligono convesso, il massimo e il minimo esistono
e si trovano in un vertice del poligono.
Osservazione
Per determinare i punti estremi basta calcolare i valori della funzione obiettivo
nei vertici del dominio, se questo è un poligono chiuso. Se il dominio dei vincoli
è illimitato si esamina invece l'andamento delle curve di livello per determinare,
se esiste, un punto che ottimizza la funzione obiettivo.
Osservazione
Se in due vertici consecutivi la funzione obiettivo assume lo stesso valore,
essa assume quello stesso valore in tutti i punti del segmento che li unisce.
| Soluzione del problema | 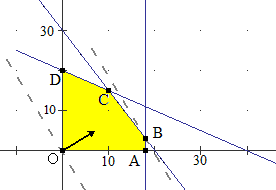 |
|
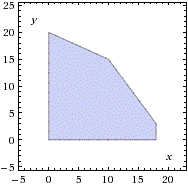
L'area ammissibile è data dal poligono OABCD, con O=(0,0), A=(18,0), B=(18,3), C=(10,15), D=(0,20). Poiché il dominio dei vincoli è un poligono chiuso, calcoliamo i valori della funzione obiettivo, z, nei vertici: z(O) = 0, z(A) = 288 000, z(B) = 318000, z(C) = 310000, z(D) = 200000. La f.o. ha un massimo in B con una produzione settimanale x =18, y =3 |
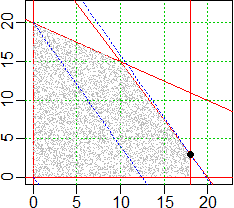
# I grafici con R
# La scelta della porzione di piano (eventualmente poi
# ritraccio la rappresentazione delle rette)
plot(c(0,22),c(0,22),type="n",xlab="", ylab="")
abline(v=axTicks(1), h=axTicks(2), col="green3",lty=3)
# le rette che delimitano il problema
# x=0;x=18;y=0; 3x+2y=60: y=-3/2*x+30; x+2y=40: y=-x/2+20
abline(v=c(0,18), col="red"); abline(h=0, col="red")
abline(30,-3/2,col="red"); abline(20,-1/2,col="red")
# la "punteggiatura" della parte interna
xa <- 0; xb <- 20; ya <- 0; yb <- 20
np <- 1e4 # numero dei punti ( po[i],pv[i] )
po <- xa+runif(np)*(xb-xa); pv <- ya+runif(np)*(yb-ya)
c1 <- function(x,y) y < 20-x/2
c2 <- function(x,y) y < 30-3*x/2
c3 <- function(x,y) x < 18
for(i in 1:np) {x <- po[i]; y <- pv[i]; if( c1(x,y)&c2(x,y)&c3(x,y)) points(x,y,pch=".",col="grey")}
# La funz. da massimizzare z = A*x + B*y (y = -A/B*y+z/B)
A <- 16000; B <- 10000
# Le linee di livello della funzione obiettivo
M <- 0; h <- function(x) -A/B*x+M/B; curve(h,add=TRUE,col="blue",lty=3)
M <- 20e4; h <- function(x) -A/B*x+M/B; curve(h,add=TRUE,col="blue",lty=3)
M <- 31.8e4; h <- function(x) -A/B*x+M/B; curve(h,add=TRUE,col="blue",lty=3)
# Le coordinate del punto A
f <- function(x) 30-3*x/2; f(18)
points(18,f(18),pch=19)
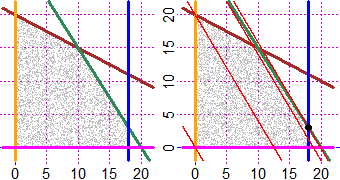
# Più rapidamente (immagini sopra a destra):
source("http://macosa.dima.unige.it/r.R")
P = function(x,y) (x+2*y <= 40) & (3*x+2*y <= 60) & (0 <= x) & (x <= 18) & (0 <= y)
HF = 3; BF = 3
Plane(-2,22, -2,22)
diseq2(P,0, "grey") # Dove P > 0 ovvero P = 1
diseq2(P,0, "grey")
# Per visualizzare il dominio bastano le righe precedenti. Per visualizzarne i limiti:
f1 = function(x,y) x+2*y -40
f2 = function(x,y) 3*x+2*y - 60
f3 = function(x,y) x
f4 = function(x,y) x - 18
f5 = function(x,y) y
CURVE(f1,"brown"); CURVE(f2,"seagreen"); CURVE(f3,"orange")
CURVE(f4,"blue"); CURVE(f5,"magenta")
#
F = function(x,y) 16000*x + 10000*y - M
M=0; CUR(F,"red")
M=2e5; CUR(F,"red")
M=3e5; CUR(F,"red")
# Capisco che la soluzione è l'intersezione tra f2 e f4
# f2; 3*x+2*y - 60 = 0 -> y = (60-3*x)/2
f=function(x) (60-3*x)/2; f(18)
# 3 La soluzione è x=18, y=3
POINT(18,f(18),"black")
M = 16000*18+10000*3; M
# 318000 il massimo
CUR(F,"red"); POINT(18,f(18),"black")
Osservazione (importanza della rappresentazione grafica).
La soluzione di un problema di programmazione lineare a due variabili è semplice in quanto
è possibile la rappresentazione grafica del campo di scelta che permette di individuare
con rapidità i vertici tra i quali deve essere ricercato l'ottimo. Ma se si tralasciasse
di fare tale rappresentazione la mole dei calcoli sarebbe notevolmente superiore.
I vertici ammissibili sono quelli che sono intersezione di due vincoli intesi come
eguaglianze e soddisfano le altre disuguaglianze.
Quindi se non si avesse la rappresentazione grafica occorrerebbe risolvere tutti i sistemi
e fare le opportune verifiche per accertare quali sono i vertici della regione ammissibile.
Su queste considerazioni si basano i metodi per risolvere problemi di programmazione lineare
in n variabili, discussi nel prossimo paragrafo.
| Vediamo, rapidamente, come il problema 1, richiamato a lato, potrebbe essere risolto automaticamente con R usando la funzione simplex. Possiamo usarla "a scatola nera". Essa si basa sul metodo del simplesso il cui funzionamento è descritto più avanti. |
|
library(boot) # Carico la libreria contenente "simplex":
# I vincoli:
A11 <- c(1,2); b11 <- 40 # quelli ≤
A12 <- c(3,2); b12 <- 60
A13 <- c(1,0); b13 <- 18
A21 <- c(1,0); b21 <- 0 # quelli ≥
A22 <- c(0,1); b22 <- 0
# Il probl. da massimizzare:
a1 <- c(16e3, 10e3)
simplex(A1=rbind(A11,A12,A13), A2=rbind(A21,A22), a=a1,
b1=c(b11,b12,b13), b2=c(b21,b22), maxi=TRUE)
Maximization Problem with Objective Function Coefficients
x1 x2
16000 10000
Optimal solution has the following values
x1 x2
18 3
The optimal value of the objective function is 318000
# a1: i coefficienti della funzione obiettivo
# A1: matrice avente per righe i coeff. dei vincoli <=
# b1: i termini noti
# A2: matrice avente per righe i coeff. dei vincoli >=
# b2: i termini noti
# maxi: TRUE o FALSE se probl. di max/min
# rbind: serve per costruire le matrici riga per riga
Nota. Se ci sono delle relazioni "≥" o dei vincoli di eguaglianza non sempre l'algortimo impiegato da R (e più in generale l'algortimo del simplesso spiegato sotto) funziona. Vi sono dei trucchi per risolvere il problema, di cui si può trovare traccia nella guida di R relativa alla voce "simplex". Noi non vedremo casi che non siano affrontabili geometricamente o con l'algortimo incorporato in R. Comunque questi casi sono affrontabili con WolframALpha, nel modo indicato in fondo alla scheda.
 Problemi di PL in tre o più variabili riconducibili a due – metodo grafico
Problemi di PL in tre o più variabili riconducibili a due – metodo grafico
|
|
|||||||||||||||||||||||||||||||||||||
|
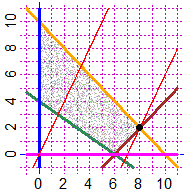
Mi sono ricondotto a due variabili. Si ottiene il massimo in (8, 2, 0) con z = 54. source("http://macosa.dima.unige.it/r.R")
f1 = function(x,y) x-y-6; f2 = function(x,y) 2*x+3*y-12
f3 = function(x,y) x+y-10; f4 = function(x,y) x; f5 = function(x,y) y
P = function(x,y)
f1(x,y)<=0 & f2(x,y)>=0 & f3(x,y)<=0 & f4(x,y)>=0 & f5(x,y)>=0
Plane(-1,11, -1,11)
diseq2(P,0, "grey"); diseq2(P,0, "grey")
CURVE(f1,"brown"); CURVE(f2,"seagreen"); CURVE(f3,"orange")
CURVE(f4,"blue"); CURVE(f5,"magenta")
F = function(x,y) 40+2*x-y - M
M=40; CUR(F,"red")
# Capisco che la soluzione è l'intersezione tra f3 e f1
f=function(x) 10-x; g=function(x) x-6; a=soluz2(f,g,0,10);b=f(a); a;b
# 8 2 La solzione è x=8, y=2
M = 40+2*8-2; M
# 54
M=54; CUR(F,"red"); POINT(8,2,"black")
|
 |
| Vediamo, comunque, come i calcoli sarebbero affrontabili con R (senza ricondurmi a 2 variabili): |
library(boot) # I vincoli:
A11 <- c(3,1,2); b11 <- 26 # quelli ≤
A12 <- c(1,0,3); b12 <- 18
A21 <- c(1,0,0); b21 <- 0 # quelli ≥
A22 <- c(0,1,0); b22 <- 0
A23 <- c(0,0,1); b23 <- 0
A31 <- c(1,1,1); b31 <- 10 # quelli =
a1 <- c(6,3,4)
simplex(A1=rbind(A11,A12),A2=rbind(A21,A22,A23),A3=A31,a=a1,
b1=c(b11,b12), b2=c(b21,b22,b23), b3=b31,maxi=TRUE)
Maximization Problem with Objective Function Coefficients
x1 x2 x3
6 3 4
Optimal solution has the following values
x1 x2 x3
8 2 0
The optimal value of the objective function is 54
# a1: i coefficienti della funzione obiettivo
# A1: matrice avente per righe i coeff. dei vincoli <=
# b1: i termini noti
# A2: matrice avente per righe i coeff. dei vincoli >=
# b2: i termini noti
# A3: matrice avente per righe i coeff. dei vincoli =
# b3: i termini noti
# maxi: TRUE o FALSE se probl. di max/min
# rbind: serve per costruire le matrici riga per riga
 Problemi di PL in tre variabili – metodo grafico
Problemi di PL in tre variabili – metodo grafico
Problema 3
Un agricoltore vuole coltivare nel suo terreno tre prodotti P, Q, R. La superficie massima utilizzabile è di 40 ettari. Per ogni ettaro coltivato a P occorrono 20 giornate di lavoro, 10 per ognuno coltivato a Q, 15 per ognuno coltivato a R. In un anno dispone di 600 giornate di lavoro di operai. La coltivazione di R non può superare i 20 ettari. Per P si ha un utile di 300000 U per ettaro, per Q si ha un utile di 200000 U per ettaro, per R si ha un utile di 350000 U per ettaro. Determinare come utilizzare il terreno per conseguire il massimo utile.
| max | z = 300 x1 + 200 x2 + 350x3 | ||
| x1 + x2 + x3 ≤ 40 | 0 ≤ x1 | ||
| 20 x1 + 10 x2 + 15 x3 ≤ 600 | 0 ≤ x2 | ||
| x3 ≤ 20 | 0 ≤ x3 |
| 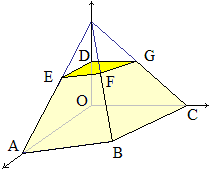 | |||||||||||||
I calcoli fatti con R:
A11 <- c(1,1,1); b11 <- 40 # quelli ≤
A12 <- c(20,10,15); b12 <- 600
A13 <- c(0,0,1); b13 <- 20
A21 <- c(1,0,0); b21 <- 0 # quelli ≥
A22 <- c(0,1,0); b22 <- 0
A23 <- c(0,0,1); b23 <- 0
a1 <- c(300,200,350)
simplex(A1=rbind(A11,A12,A13),A2=rbind(A21,A22,A23),a=a1,
b1=c(b11,b12,b13), b2=c(b21,b22,b23) ,maxi=TRUE)
Maximization Problem with Objective Function Coefficients
x1 x2 x3
300 200 350
Optimal solution has the following values
x1 x2 x3
10 10 20
The optimal value of the objective function is 12000.
Il metodo grafico è un po' laborioso e non applicabile a più di tre variabili: si può applicare il metodo algebrico.
 Problemi di PL in n variabili – metodo algebrico
Problemi di PL in n variabili – metodo algebrico
| Ottimizzare | z = c1 x1 + c2 x2 + … + cn xn | ||
| a 1 1 x1 + a 1 2 x2 + … + a 1 n xn ≤ b1 | |||
| a 2 1 x1 + a 2 2 x2 + … + a 2 n xn ≤ b2 | 0 ≤ xi , i = 1, …, n | ||
| ... | |||
a m 1 x1 + a m 2 x2 + … + a m n xn ≤ bm
|
| |
Per determinare i vertici, essendo m+n i vincoli e n le variabili occorre risolvere un numero di sistemi lineari di n equazioni (ottenute dai vincoli espressi con l'eguaglianza) in n incognite.
Tutti i possibili sistemi sono 
Non è detto che le soluzioni trovate siano tutte ammissibili, ma
Ad esempio con n = 10 variabili e 6 vincoli tecnici (in totale 6+10 vincoli) dovremmo risolvere
 Problemi di PL in n variabili – metodo del simplesso
Problemi di PL in n variabili – metodo del simplesso
La tecnica algebrica di ricerca dell'ottimo è semplice, ma inefficiente per problemi in cui l'insieme ammissibile
ha molti vertici: l'algoritmo del simplesso è una procedura efficiente che risolve il problema.
L'algoritmo del simplesso, in effetti, risolve problemi in cui tutti i vincoli tecnici sono rappresentati da equazioni:
i vincoli sono quindi m equazioni ed n disequazioni di positività delle variabili.
È possibile comunque applicarlo ad un problema generale trasformando le disequazioni in equazioni: si aggiungono delle variabili fittizie, dette variabili slack con coefficiente zero nella funzione obiettivo.
|
|
|||||||||||||||||||||||||||||
Il metodo del simplesso, invece di calcolare il valore della funzione obiettivo in tutti i vertici ammissibili, permette di calcolare il valore della funzione in un dato vertice e di scegliere il successivo in modo che la funzione obiettivo "migliori" e così via fino a giungere all'ottimo più velocemente.
| Algoritmo "grafico" del simplesso | |
| 1. | Si considera un vertice iniziale ammissibile. |
| 2. | Si confronta il vertice prescelto con quelli ad esso adiacenti. |
| 3. | Se tra questi ultimi vertici se ne trova uno "migliore" si prende in considerazione quest'ultimo e si ripete il confronto tornando al punto 2. |
| 4. | In caso contrario l'ultimo vertice considerato è quello ottimo. |
Il numero di vertici che occorre percorrere è presumibilmente inferiore al n° totale , poiché ad ogni iterazione ci si avvicina alla soluzione ottimale e quindi molti vertici vengono esclusi dalla necessità di esame.
Soluzione problema 3 con metodo del simplesso
- Passo 1 (Scelta di una prima soluzione ammissibile)
Posti x1 = x2 = x3 = 0, dal sistema dei vincoli si ricava x4 =40, x5 =120, x6 = 20 e si ha la prima soluzione ammissibile di base
(0,0,0,40,120,20) che corrisponde al valore z = 0.
- Passo 2
Si vuole ora passare ad un’altra soluzione ammissibile che aumenti il valore di z in modo che una variabile
fra quelle prima nulle prenda valore positivo ed un’altra tra quelle prima positive diventi nulla.
Il sistema dei vincoli risolto rispetto a x4, x5 , x6 è
x4 = 40 - x1 - x2 - x3
x5 = 120 - 4 x1 - 2 x2 - 3 x3
x6 = 20 - x3.
Dall’esame di z = 300 x1 + 200 x2 + 350 x3 + 0 x4 + 0 x5 + 0 x6, si vede che il massimo incremento di z
si ha incrementando x3 e dall’esame dei vincoli si vede che il massimo valore attribuibile a x3 è 20,
da cui x6 = 0 (si deve rispettare la condizione xi ≥ 0 - i =1, …, 6).
Si ricava quindi la seconda soluzione ammissibile (0,0,20,20,60,0) con z = 300 x1 + 200 x2 + 350 (20–x6) + 0 x4 + 0 x5 + 0 x6
= 7000.
Si dice che x3 è entrata nella base e x6 è uscita dalla base.
Le variabili della base sono quelle non nulle è cioè x3, x4, x5.
Cerchiamo ora di passare da questa soluzione ad una ad essa adiacente che aumenti il valore di z. Una soluzione di base è adiacente ad un'altra se ha le stesse variabili di base
della precedente tranne una; dobbiamo fare in modo che una fra x3, x4, x5 diventi nulla (esce dalla base), inserendo nella nuova base x1, x2 o x6.
- Passo 3
Esaminando z = 300 x1 + 200 x2 + 350 (20–x6) + 0 x4 + 0 x5 + 0 x6 = 7000 + 300x1 +200 x2 – 350 x6, si sceglie,
tra le variabili, quella che migliora la funzione obiettivo e quindi x1.
Ci chiediamo ora qual è il massimo valore attribuibile a x1 affinché una fra x3, x4, x5
si annulli, lasciando però ≥ 0 tutte le altre.
Si riscrive il sistema dei vincoli ricavando x3, x4, x5 rispetto alle variabili fuori dalla base, ottenendo
x3 = 20 - x4
x4 = 40 + x6 - x1 - x2
x5 = 60 - 4 x1 - 2 x2 + 3 x3.
individuando la terza soluzione ammissibile (15,0,20,5,0,0) con z = 11.500+50 x2 - 75 x5 – 125 x6.
-
Passo 4
Entra nella base x2. Scriviamo il sistema dei vincoli esprimendo x1, x3, x4 rispetto alle variabili fuori dalla base
e si determina il valore migliore x2 = 10. Si ottiene la quarta soluzione ammissibile (10,10,20, 0, 0,0) con
z = 12000 - 100 x4 - 50 x5 – 100 x6.
Il valore di z non si può migliorare ulteriormente poiché tutti i coefficienti sono negativi e le variabili entrando nella base ridurrebbero il valore di z. Quindi (10,10,20,0,0,0) è la soluzione ottima.
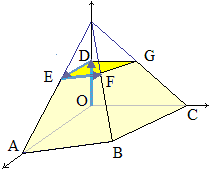 |
Sequenza dei vertici: O = (0,0,0,40,120,20) D = (0,0,20,20,60,0) E = (15,0,20,5,0,0) F = (10,10,20,0,0,0) |
| Schema algebrico del simplesso | |
| 1. | individuazione di una prima soluzione di base ammissibile. Se tale soluzione non è ottima: |
| 2. | scrittura del sistema dei vincoli in funzione di tale base. |
| 3. | ricerca di una nuova soluzione di base ammissibile mediante individuazione della variabile entrante nella base e di quella uscente dalla base. |
| 4. | determinazione della nuova soluzione di base ammissibile. |
| 5. | valutazione della funzione per stabilire se si è trovata la soluzione ottima. Si ripetono i passi da 2 a 5 fino a che si trova la soluzione ottimale |
Approfondimenti (nella versione inglese di WikiPedia).
Strumenti semplici per elaborazioni informatiche possono essere trovate in R (cercare "linear programming" nel documento "Search Engine & Keywords" a cui si accede dal "Html Help" del menu Help; ricorda che occorre caricare library(boot)). Gli esempi visti dovrebbero comunque essere sufficienti.
Altre nozioni in inglese sul tema possono essere trovate in http://www.WolframAlpha.com
scrivendo linear programming (selezionando sia "a word" che "a mathematical def."), optimization
(sia "a general topic" che "a class of mathematical terms"),
convex optimization theory e
simplex method nell'apposito box
(vedi anche famous mathematical game).
Il problema precedente con WolframAlpha lo posso risolvere così:
maximize[ {30x+20y+35z, {x+y+z<=40 && 2x+y+1.5z<=60 && 0<=z<=20 && x>=0 && y>=0} } ]
[al posto di "&&" puoi usare "and"; per il minimo usa "minimize"]
Nota:
un solo "&" può dar luogo ad errori; prova ad usare:
maximize[ {30x+20y+35z, {x+y+z<=40 & 2x+y+1.5z<=60 & 0<=z<=20 & x>=0 & y>=0} } ]
Ottengo che il massimo vale 1200 (ho diviso per 10000 la funzione originale) ed è in (10,10,20).
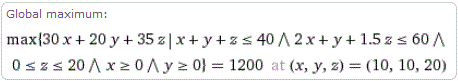
Il secondo problema lo potevo risolvere con:
maximize[ {6x+3y+4z, {x+y+z=10 && 3x+y+2z<=26 && x+3z<=18 && x>=0 && y>=0 && z>=0} } ]
I comandi possono assumere varie forme. Ad es. il primo problema posso risolverlo con:
maximize 16000x+10000y in x+2y<=40 && 3x+2y<=60 && 0<=x<=18 && 0<=y
oltre che con:
maximize[z,{ z=16000x+10000y && x+2y<=40 && 3x+2y<=60 && 0<=x<=18 && 0<=y},{x,y,z}]
I vincoli posso rappresentarli con:
plot x+2y<=40 && 3x+2y<=60 && 0<=x<=18 && 0<=y