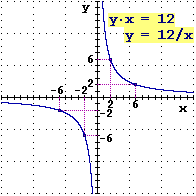Proporzionalita' inversa

• Vi sono altre situazioni di inversa proporzionalità che hanno suggerito l'introduzione di una nuova grandezza fisica. Se voglio aprire con un dito una porta socchiusa, spingendo vicino ai cardini su cui essa poggia e ruota non ci riesco; man mano che mi allontano dai cardini è minore la forza che devo applicare con il dito: più precisamente, la forza da applicare alla porta è inversamente proporzionale alla distanza dall'asse di rotazione della porta.

Più in generale se devo produrre una rotazione attorno a un punto O il mio effetto dipende sia dalla forza F che applico che dalla distanza R che (la retta lungo cui agisce) F ha da O. A parità di effetto il prodotto F·R è costante, e viene detto momento meccanico (di F rispetto ad O).

Questo fenomeno si può spiegare impiegando il concetto di lavoro discusso sopra. Infatti - vedi figura (1) - R è proporzionale allo spostamento s che si deve compiere, e questo (a parità di lavoro: quello per eseguire la rotazione in questione) è inversamente proporzionale alla forza F da applicare.
Ad esempio nel caso della figura (2), in cui A dista dal centro del bullone il triplo rispetto a B, se per svitare impugno la chiave in A devo tirare con una forza pari a 1/3 di quella che dovrei esercitare se l'impugnassi in B.
Nel caso si provi a mantenere un braccio teso in varie posizioni tenendo un oggetto abbastanza pesante in mano, nonostante che la distanza dell'oggetto dalla spalla non cambi, ci si accorge subito che la posizione col braccio orizzontale - posizione a destra nella figura (3) - è quella in cui è più difficile impedire che il braccio ruoti; quella verticale è quella in cui è più facile. Ciò accade poiché cambiando l'inclinazione del braccio cambia la distanza dalla spalla della retta lungo cui agisce la forza-peso, e tale distanza è massima quando il braccio è orizzontale, è nulla se il braccio è verticale.

La stadera - figura (4) - ha fissi il pesetto P2 e la distanza R1 del punto a cui è appeso il piatto dal punto in cui è tenuta sospesa la stadera. Quando sul piatto metto un oggetto di peso P1 la posizione che deve assumere P2 perché la stadera vada in equilibrio è ad una distanza R2 tale che il momento P1·R1 eguagli P2·R2, ovvero P1 = R2·P2/R1. Dalla lettura di R2 ricavo il valore di P1, come posso fare facilmente utilizzando un'apposita scala graduata collocata sull'asta. Con un pesetto P2 piccolo posso misurare pesi di valore molto alto (se R2 può arrivare ad essere 20 volte R1 posso misurare pesi pari a 20 volte P2).

NOTA. Nel caso di una bicicletta da corsa i pedali sono fissati alle scarpette per cui alla forza del piede che spinge un pedale si "accoppia" la forza (minore) di quello che tira in su l'altro: il momento meccanico in questo caso è la somma dei momenti prodotti dai due piedi. Nel caso della bici e più in generale dei motori (che consumando energia elettrica o combustibile o utilizzando vento, acqua od altre risorse, producono la rotazione di un "albero motore" che, mediante cinghie o ingranaggi, trasmette il movimento a particolari macchinari) invece che di momento meccanico spesso si parla di coppia motrice. Ad es. se sul manuale d'uso di un ciclomotore si legge che la coppia motrice massima è di 0.40 kg·m e che il rapporto di trasmissione più basso è 1/20 (la velocità di rotazione della ruota è 1/20 di quella dell'albero motore), ciò significa che il momento massimo che può produrre la ruota posteriore del ciclomotore è 0.40·20 = 8 kg·m (riducendosi la velocità aumenta in modo inversamente proporzionale la forza, e quindi il momento); se il raggio della ruota è di 20 cm la forza massima con cui la ruota, facendo attrito sul terreno, può spingere nella direzione di marcia (ovvero la forza che, in pianura, è sufficiente esercitare per trattenere il ciclomotore) è: Forza = Momento/DistanzaDalCentro = 8 kg·m / 0.20 m = 40 kg.

Una relazione del tipo (1) (con k diverso da 0) viene detta relazione di proporzionalità inversa.	k (1) grandezza2 = —————————— grandezza1

Il nome deriva dall'analogia con la relazione di proporzionalità. Infatti (1) può essere scritta nella forma (2), cioè come una relazione di proporzionalità tra grandezza2 e l'inverso (o reciproco) di grandezza1.	1 (2) grandezza2 = —————————— · k grandezza1

A volte invece che di proporzionalità si parla di proporzionalità diretta, per sottolineare la differenza dalla proporzionalità inversa.

Si parla anche di proporzionalità quadratica e cubica per indicare relazioni del tipo grandezza2 = k · (grandezza1)² e grandezza2 = k · (grandezza1)³, in cui vi è proporzionalità tra una grandezza e il quadrato o il cubo dell'altra.

Mentre la relazione di proporzionalità y=kx può essere espressa come y/x=k (il rapporto tra le due variabili è costante), la relazione di inversa proporzionalità y=k/x può essere espressa come x·y=k (il prodotto tra le due variabili è costante).
Mentre i grafici delle relazioni di proporzionalità sono rette, quelli delle relazioni di inversa proporzionalità sono iperboli [ figure 2].

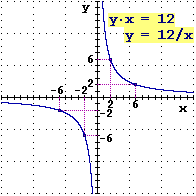
Esempi di relazione di inversa proporzionalità:
• la relazione tra le dimensioni a e b dei rettangoli di area fissata A: a·b = A
• la relazione tra l'intensità della forza F e la lunghezza s che deve avere la traiettoria lungo cui si esercita tale forza per produrre un certo lavoro L: F·s = L

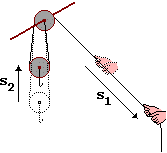
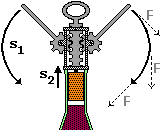
Su quest'ultima relazione si basano le macchine semplici "vantaggiose", come la carrucola mobile e il cavatappi sotto raffigurati: il lavoro da generare è distribuito su una traiettoria di lunghezza maggiore in modo da ridurre in modo inversamente proporzionale la forza da esercitare.

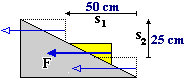
Anche il dispositivo a destra (oggetto liscio su un piano inclinato liscio con pendenza minore di 1) è vantaggioso: per sollevare l'oggetto esercito orizzontalmente una forza su di esso per una distanza maggiore dello spostamento verticale, e quindi con una intensità minore di quella che applicherei spingendolo o tirandolo verticalmente.
Nota.Con s indichiamo la lunghezza dello spazio percorso nella direzione in cui è esercitata la forza, non la lunghezza del vettore spostamento tra punto di applicazione iniziale e punto di applicazione finale: nell'es. ora visto prendo come s₁ solo la componente orizzontale dello spostamento del punto di applicazione, nel caso del cavatappi s₁ è invece la lunghezza dell'arco descritto dal punto di applicazione in quanto la forza è esercitata lungo una direzione variabile, via via tangente a tale arco.

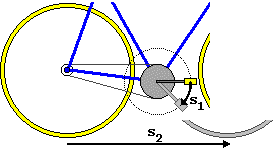
La bicicletta, invece, "moltiplica" lo spostamento prodotto dai pedali (s₂ è maggiore di s₁), per cui la forza da esercitare con i piedi per affrontare una salita è maggiore di quella che occorre esercitare camminando.

• In una bicicletta dotata di cambio è possibile modificare il rapporto tra spazio percorso dalla ruota e spazio percorso dal pedale (ossia il fattore per cui viene moltiplicato lo spazio percorso dal pedale); all'aumentare della pendenza della strada conviene diminuire questo rapporto, in modo da non dover aumentare troppo la forza da esercitare sui pedali. Ciclisti dello stesso peso e con lo stesso modello di bicicletta possono usare rapporti diversi per affrontare la stessa salita; chi usa un rapporto più alto esercita una forza maggiore, ma se va su alla stessa velocità degli altri non è detto che abbia maggiore potenza: conta non solo la forza che si esercita sui pedali, ma anche la velocità con cui li si fa ruotare. Se X usa un rapporto doppio e sale alla stessa velocità di Y vuol dire che spinge sul pedale con forza doppia e mezza velocità (per produrre lo stesso avanzamento lungo la strada s₂ attua sul pedale uno spostamento s₁ dimezzato).
Analogamente, viaggiando con un motociclo dotato di cambio automatico, a parità di posizione della manopola di alimentazione (acceleratore) all'aumentare della forza che la moto deve vincere (per un aumento della pendenza o del carico o del vento o …) diminuisce in maniera inversamente proporzionale la velocità della moto: se la forza da vincere raddoppia la velocità dimezza. Fissata l'alimentazione (la quantità di benzina fornita nell'unità di tempo), la velocità e la forza prodotta (nella direzione del movimento) sono inversamente proporzionali. Il loro prodotto (la costante di proporzionalità) viene chiamato potenza: P = F·v. Il cambio ha quindi la funzione di cambiare la forma di utilizzo della potenza prodotta dal motore (o dall'uomo, nel caso della bici), variando in maniera inversamente proporzionale F e v.
• La potenza può essere espressa, oltre che come prodotto tra la velocità v e la forza F prodotta (nella direzione del movimento), anche come rapporto tra il lavoro L prodotto e il tempo t impiegato a produrlo. Infatti, se indichiamo con s lo spostamento lungo la direzione di F, possiamo scrivere:
P = F·v = F·(s/t) = (F·s)/t = L/t
In altre parole, la potenza può essere descritta come la velocità con cui viene prodotto il lavoro.
I motori funzionano trasformando forme di energia diverse (termica, elettrica, chimica, ...) in energia meccanica, ossia lavoro. Queste altre forme di energia possono essere espresse con la stessa unità di misura con cui viene espresso in genere il lavoro, il Joule (simbolo J), che rappresenta il lavoro per esercitare una forza di

1 Newton per 1 metro: 1 J = 1 N·m. Quindi la potenza, essendo la velocità con cui viene prodotta l'energia, si esprime in Joule al secondo; questa unità di misura viene chiamata Watt (simbolo W): 1 W = 1 J/s. Dato che un motore non riesce a trasformare tutta l'energia che lo alimenta in lavoro a causa di attriti e ad altre forme di dispersione, si può considerare accanto alla potenza prodotta la potenza assorbita (velocità con cui viene consumata energia). La distinzione tra potenza in ingresso e potenza in uscita si può fare anche per altri dispositivi che trasformano energia (dispositivi per il riscaldamento, l'illuminazione, la produzione di suoni, ...).
Il lavoro, e più in generale l'energia, può essere espresso anche come prodotto tra potenza e tempo:
P = L/t → L = P·t
Come unità di misura della potenza in campo motoristico si usa anche il cavallo-vapore (in europa continentale pari a 735.5 W, con simbolo CV in Italia e altri simboli in altri paesi; nei paesi anglosassoni è indicato HP ed è considerato pari a 745.7 W). Tenendo conto della possibilità di esprimere l'energia come potenza per tempo, per essa si usano come unità di misura anche il CV·h (cavallo vapore per ora), pari a 735.5·3600 W·s = 735.5·3600 J ≈ 2.6·10⁶ J, e il W·h (watt per ora, detto anche "wattora", e indicato anche Wh), pari a 3600 W·s = 3.6·10³ J. Si usa anche la caloria (cal), pari a 4.1868 J (pari, circa, alla energia necessaria per far salire di 1° la temperatura di un grammo d'acqua); è essenzialmente dovuta al birraio Joule la dimostrazione che il calore è un forma di energia (vedi).
Viene chiamato "principio di conservazione dell'energia" il fatto che in un sistema isolato l'energia totale si conserva. L'energia meccanica di un corpo può essere scomposta in energia potenziale (mgh se m è la massa e h è l'altezza rispetto ad un piano di riferimento) ed energia cinetica (mv²/2 se v è la velocità del corpo). Se non ci sono dispersioni (attrito, resistenza dell'aria, …) l'energia meccanica si conserva.

• Vi sono altre situazioni di inversa proporzionalità che hanno suggerito l'introduzione di una nuova grandezza fisica. Se voglio aprire con un dito una porta socchiusa, spingendo vicino ai cardini su cui essa poggia e ruota non ci riesco; man mano che mi allontano dai cardini è minore la forza che devo applicare con il dito: più precisamente, la forza da applicare alla porta è inversamente proporzionale alla distanza dall'asse di rotazione della porta.

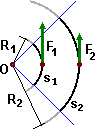
Più in generale se devo produrre una rotazione attorno a un punto O il mio effetto dipende sia dalla forza F che applico che dalla distanza R che (la retta lungo cui agisce) F ha da O. A parità di effetto il prodotto F·R è costante, e viene detto momento meccanico (di F rispetto ad O).

Questo fenomeno si può spiegare impiegando il concetto di lavoro discusso sopra. Infatti - vedi figura (1) - R è proporzionale allo spostamento s che si deve compiere, e questo (a parità di lavoro: quello per eseguire la rotazione in questione) è inversamente proporzionale alla forza F da applicare.
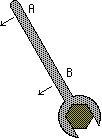
Ad esempio nel caso della figura (2), in cui A dista dal centro del bullone il triplo rispetto a B, se per svitare impugno la chiave in A devo tirare con una forza pari a 1/3 di quella che dovrei esercitare se l'impugnassi in B.
Nel caso si provi a mantenere un braccio teso in varie posizioni tenendo un oggetto abbastanza pesante in mano, nonostante che la distanza dell'oggetto dalla spalla non cambi, ci si accorge subito che la posizione col braccio orizzontale - posizione a destra nella figura (3) - è quella in cui è più difficile impedire che il braccio ruoti; quella verticale è quella in cui è più facile. Ciò accade poiché cambiando l'inclinazione del braccio cambia la distanza dalla spalla della retta lungo cui agisce la forza-peso, e tale distanza è massima quando il braccio è orizzontale, è nulla se il braccio è verticale.

(1) (2) (3)

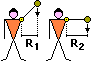(4)

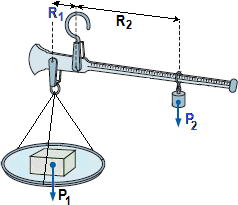La stadera - figura (4) - ha fissi il pesetto P2 e la distanza R1 del punto a cui è appeso il piatto dal punto in cui è tenuta sospesa la stadera. Quando sul piatto metto un oggetto di peso P1 la posizione che deve assumere P2 perché la stadera vada in equilibrio è ad una distanza R2 tale che il momento P1·R1 eguagli P2·R2, ovvero P1 = R2·P2/R1. Dalla lettura di R2 ricavo il valore di P1, come posso fare facilmente utilizzando un'apposita scala graduata collocata sull'asta. Con un pesetto P2 piccolo posso misurare pesi di valore molto alto (se R2 può arrivare ad essere 20 volte R1 posso misurare pesi pari a 20 volte P2).

NOTA. Nel caso di una bicicletta da corsa i pedali sono fissati alle scarpette per cui alla forza del piede che spinge un pedale si "accoppia" la forza (minore) di quello che tira in su l'altro: il momento meccanico in questo caso è la somma dei momenti prodotti dai due piedi. Nel caso della bici e più in generale dei motori (che consumando energia elettrica o combustibile o utilizzando vento, acqua od altre risorse, producono la rotazione di un "albero motore" che, mediante cinghie o ingranaggi, trasmette il movimento a particolari macchinari) invece che di momento meccanico spesso si parla di coppia motrice. Ad es. se sul manuale d'uso di un ciclomotore si legge che la coppia motrice massima è di 0.40 kg·m e che il rapporto di trasmissione più basso è 1/20 (la velocità di rotazione della ruota è 1/20 di quella dell'albero motore), ciò significa che il momento massimo che può produrre la ruota posteriore del ciclomotore è 0.40·20 = 8 kg·m (riducendosi la velocità aumenta in modo inversamente proporzionale la forza, e quindi il momento); se il raggio della ruota è di 20 cm la forza massima con cui la ruota, facendo attrito sul terreno, può spingere nella direzione di marcia (ovvero la forza che, in pianura, è sufficiente esercitare per trattenere il ciclomotore) è: Forza = Momento/DistanzaDalCentro = 8 kg·m / 0.20 m = 40 kg.

Due grandezze non proporzionali possono comunque avere variazioni proporzionali [

proporzionalità]. Anch'esse hanno come grafico una retta, ma non passante per (0,0).
Ad es. in alcune produzioni i costi totali aumentano in proporzione all'aumento del n° di pezzi prodotti (C_T = C_F + C_I · n, dove n = "n° di pezzi prodotti nell'anno", C_T = "costi totali annui", C_I = "costi incorporati in un pezzo").
Il grafico interseca l'asse verticale non in 0 ma in corrispondenza del valore dei costi fissi (C_F).
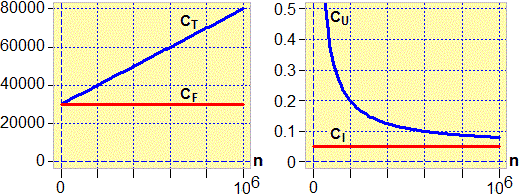
Nel caso raffigurato sotto a sinistra C_T = 30 000 + 0.05 n.
(potrebbero essere i costi di una piccola tipografia che stampa fogli in un unico formato con 0.05 € di costi incorporati in ogni foglio stampato – per carta, inchiostro, energia elettrica, ... – e 30 mila € di spese fisse annue – per un addetto alle macchine, l'affitto, …).

Analogamente vi sono grandezze che, pur non essendo inversamente proporzionali, hanno variazioni inversamente proporzionali. Il loro grafico ha forma simile a quello di una relazione di inversa proporzionalità, ma, rispetto a questo, è traslato. Anche questi grafici vengono chiamati iperboli.
Ad es., nel caso delle produzioni di cui sopra, il costo unitario ha una variazione inversamente proporzionale alla variazione del n° di pezzi prodotti (C_U = C_F / n + C_I). Il grafico è come quello di C_U = C_F / n ma innalzato di un un valore pari a C_I (il costo unitario non può essere ridotto a piacere in quanto i costi incorporati non possono essere eliminati).
Nel caso dell'esempio precedente si ha (figura sopra a destra) C_U = 30 000 / n + 0.05.
(all'aumentare dei fogli stampati l'incidenza delle spese fisse sul costo di un singolo foglio tende a ridursi, e il costo unitario tende a coincidere con i soli costi incorporati per materie prime ed energia).
Hanno un grafico dall'andamento simile (ma capovolto) il guadagno totale e il guadagno unitario (guadagno: ricavo − costi) in funzione del volume di produzione (e vendita): vedi qui.

Sopra abbiamo accennato all'HP, unità di misura di potenza usata nel sistema anglosassone; altre unità di misura usate nel sistema anglosassone sono il pollice, il piede, lo yard, il miglio (di lunghezza), la libbra, l'oncia (di peso), il gallone, la pinta (di capacità).
Ricordiamo (vedi) che nel caso delle temperature spesso si usano i gradi Fahrenheit (�F), le cui relazioni con i gradi Celsius (�C) e Kelvin (�K) sono, indicando con TF, TC e TK la stessa temperatura espressa in queste tre scale, TF = 9/5·TC+32 (0�C → 32�F, 100�C → 212�F, 9/5 = 180/100), TC = 5/9·(TF−32), TK = TC+273.15 (0�K → −273.15�C).
Per approfondimenti, e "unità" non in ambito fisico, vedi WolfrAmalpha.
Per misurare le estensioni superficiali si usa anche l'ara, pari a 100 m² (deriva dal latino ara, ossia "aia": un quadrato con 10 m di lato pu� essere considerata la misura approssimativa di un'aia); pi� usato � l'ettaro, pari a 100 are (ossia ad un quadrato con 100 m di lato), simboleggato con ha.
In fisica e in altre scienze applicate è spesso utile ricorrere alla analisi dimensionale, ossia al controllo dei calcoli svolti utilizzando solo le unità di misura o i nomi o i simboli delle grandezze coinvolte e riconducendosi alle grandezze fondamentali. Ad esempio una velocità può essere descritta come [lunghezza][tempo]⁻¹ o con LT⁻¹ o con [m][s]⁻¹ o con ms⁻¹, a seconda delle convenzioni usate (nel secondo uso, la massa è indicata con M). Per approfondimenti vedi WolfrAmalpha.