Proporzionalità

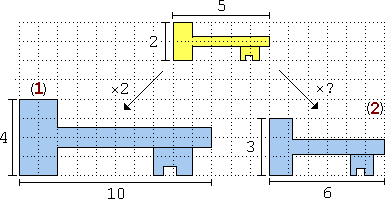
A fianco è raffigurata una chiave e due sue riproduzioni.    La riproduzione (2) è sproporzionata: è troppo tozza. [clicca le immagini per ingrandirle]

Per precisare questa impressione possiamo osservare che, mentre la riproduzione (1) è stata ottenuta moltiplicando tutte le distanze per 2 (la lunghezza della chiave è passata da 5 a 10, l'altezza dell'impugnatura è passata da 2 a 4, …), nel caso della riproduzione (2) alcune distanze sono state moltiplicate per un numero, altre per un altro (la lunghezza è passata da 5 a 6, cioè è stata moltiplicata per 6/5 = 1.2; l'altezza è passata da 2 a 3, cioè è stata moltiplicata per 3/2 = 1.5).

   In formula possiamo scrivere:   distanze in (1) = (distanze originali) · 2

   Una relazione del tipo:  grandezza 2 = grandezza 1 · k (dove k è un numero fissato diverso da 0), viene detta relazione di proporzionalità. Il numero k viene chiamato fattore di proporzionalità.

  Nel caso in cui le grandezze siano distanze, come nell'esempio precedente, k viene chiamato scala (o fattore di scala). Se k > 1 si parla di scala di ingrandimento (nel caso precedente (1) è stata ottenuta con la scala di ingrandimento 2).
   Se k < 1 si parla di scala di riduzione (per passare da (1) alla figura originale devo dimezzare le distanze, cioè moltiplicarle per 1/2 [ = 0.5]: questa è la scala di riduzione che devo applicare).

  Se trasformo dei dati in modo proporzionale mediante un fattore k, per ritornare ai dati originali devo dividere per k, cioè applicare il fattore di proporzionalità 1/k, cioè il reciproco di k.
    Il reciproco di 2 è 1/2 (se ho moltiplicato per 2, per ritornare al valore iniziale devo prendere 1/2 del valore ottenuto, ossia moltiplicare per 1/2) e, viceversa, il reciproco di 1/2 è 2 (se ho moltiplicato per 1/2, per tornare al valore iniziale devo moltiplicare per 2); il reciproco di 3/4 è 4/3 (se ho moltiplicato per 3/4, ossia se ho diviso per 4 e moltiplicato per 3, per tornare al valore iniziale devo dividere per 3 e moltiplicare per 4, ossia moltiplicare per 4/3).

Nota.  Dividere per k equivale a moltiplicare per 1/k. Ricordare ciò è spesso comodo per i calcoli mentali e per svolgere altri calcoli che coinvolgono rapporti:
•  quanto fa  15 / 0.75? so che 0.75 = 3/4 e quindi 15/0.75 = 15/(3/4) = 15·(4/3) = 15/3·4 = 5·4 = 20.
•  quanto fa  30% / (2/3)? 30%/(2/3) = 30%·(3/2) = 90%/2 = 45%.

Esercizio

  Nella riproduzione (1) vengono mantenuti i rapporti tra le dimensioni delle diverse componenti: ad esempio nella chiave originale l'altezza dell'impugnatura è pari al 40% della lunghezza della chiave: 2/5 = 0.4 = 40%, e anche nella riproduzione (1) questo rapporto vale 4/10 = 0.4 = 40% (nella riproduzione (2) invece tale rapporto vale 3/6 = 0.5 = 50%).
    Infatti se le dimensioni di un oggetto (i due lati del tavolo o la lunghezza e l'altezza della chiave o …) vengono moltiplicate per la stessa scala, il rapporto tra tali dimensioni non viene modificato.
    Nel caso sotto raffigurato il rettangolo al centro mediante la trasformazione (b) viene rimpicciolito riproducendone i lati con le stesse misure ma usando una unità di misura dimezzata: il rapporto tra le due dimensioni non cambia: la dimensione verticale è sempre i 3 quinti di quella orizzontale.
    La trasformazione (a) invece è solo un cambio di unità di misura: le dimensioni rimangono immutate e il rapporto tra le loro misure nella nuova unità non muta: la misura della dimensione verticale (6) è sempre i 3 quinti di quella verticale (10); ovvero 6/10 = 3/5 (= 0.6 = 60%).

    Questo fatto vale in generale, per ogni coppia di grandezze proporzionali: se trasformo dei dati x1, x2, x3, … moltiplicandoli tutti per un fattore k ottengo nuovi dati y1 (= x1 · k), y2 (= x2 · k), y3 (= x3 · k), … che hanno tra di loro gli stessi rapporti che vi sono tra i corrispondenti dati originali:

y3  =  x3·k  =  x3·k  =  x3 — —— —— — y1 x1·k x1·k x1		y1  =  x1·k  =  x1·k  =  x1 — —— —— — y2 x2·k x2·k x2		...
↑ la "cancellazione" di k non modifica il risultato della divisione

    Il fatto che una trasformazione proporzionale mantenga i rapporti viene usato spesso per modificare i due termini di una divisione in modo da facilitare il confronto con un altro rapporto (primo degli esempi seguenti) o per rendere più semplice il calcolo (secondo esempio):

•  per stabilire quale tra 4/9 e 6/14 è la frazione maggiore potrei eseguire le divisioni (ottengo i risultati 0.444… e 0.428… e concludo che la prima è maggiore); ma se non ho una CT (o un cellulare) con cui effettuare i calcoli mi conviene trasformare 4/9 in  4·14/(9·14) = 4·7·2/(9·7·2) = 56/126  (ho moltiplicato i due termini per 14)  e 6/14 in  6·9/(14·9) = 54/126  (ho moltiplicato i due termini per 9), e osservare che 56>54:

4  =  4·14  =  56 — —— —— 9 9·14 126

6  =  6·9  =  54 — —— —— 14 14·9 126

•  per calcolare 1.4 / 0.04 mi conviene moltiplicare i due termini per 100 e ricondurmi a 140 / 4, poi dividerli entrambi per 2 e ricondurmi a 70 / 2, e infine ottenere 35.

•  per calcolare il rapporto tra 3/4 e 2/3 posso ricordarmi che la divisione per 2/3 è trasformabile nella moltiplicazione per il reciproco: 3/4 / (2/3) = 3/4 · (3/2) = 9/8, come osservato nella nota precedente, oppure posso procedere così:

3/4  =  (3/4)·(3/2)  =  9/8  = 9/8 —— ———— —— 2/3 (2/3)·(3/2) 1

o così:

3/4  =  3/4·4·3  =  3·3  =  9 — —— —— — 2/3 2/3·4·3 2·4 8

Esercizio 1     Esercizio 2

  Ci sono molti esempi di relazioni di proporzionalità:

•  le riproduzioni cartografiche; in questo caso non si tratta tuttavia di una relazione perfettamente proporzionale in quanto nel passaggio da una superficie sferica a una superficie piana non tutte le distanze possono essere moltiplicate esattamente per lo stesso fattore di riduzione;
•  come si determina il costo di un prodotto venduto a peso: costo = peso·U, dove U è il costo unitario, cioè il prezzo al kg [hg] se il peso è in kg [hg];
•  come si determina il costo di un viaggio in treno per percorrenze non troppo lunghe: nel 1991, fino a 1000 km di percorrenza, esprimendo il prezzo in "lire":  prezzo = (n° di chilometri percorsi)· 60;   le tariffe vengono però, poi, organizzate in fasce e approssimate con prezzi "tondi" (351 km ≤ percorrenza < 401 km tariffa = 24100, 401 km ≤ percorrenza < 451 km tariffa = 27100, mentre 401·60 = 24060, 451·60 = 27060). [ Esempio]

  Anche le relazioni tra dati originali e parti percentuali [ rapporto] e tra dati originali e ampiezze dei settori circolari [ diagrammi], per rappresentare come si ripartisce un insieme di dati rispetto al suo totale sono esempi di relazioni di proporzionalità; infatti il rapporto tra percentuale e 100 e quello tra ampiezza (in gradi) e 360 sono uguali al rapporto tra dato e totale.

               dato
percentuale = —————— ·100
              totale

            dato
ampiezza = —————— · 360 
           totale

Le formule precedenti possono essere trasformate [  Formule ] nel modo seguente, che mette in evidenza il fattore di proporzionalità tra dato e percentuale e tra dato e ampiezza:

	100 percentuale = dato · —————— totale	360 ampiezza = dato · —————— totale
Queste formule possono essere invertite prendendo come fattori di proporzionalità (per trasformare percentuale o ampiezza in dato) i reciproci.
Nel caso delle percentuali abbiamo:		totale dato = percentuale · —————— 100

  Anche altre ripartizioni proporzionali possono essere calcolate in questi due modi. Ad esempio se tre amici A, B e C giocano 20000 lire al totocalcio vincendo 120 milioni, per suddividere la vincita in parti proporzionali alle giocate di ciascuno (5000, 6000 e 9000 lire rispettivamente) possono procedere in due modi:

quota giocata vincita = ————————————— · 120 000 000 20 000

oppure

120 000 000 vincita =(quota giocata) · —————————— 20 000

Le due formule corrispondono ai due seguenti ragionamenti non formalizzati:

– A ha messo 5 mila delle 20 mila giocate, quindi gli spettano 5 ventesimi della vincita; …

– se 20 mila lire hanno "reso" 120 milioni, 1000 lire hanno reso (120 milioni)/20 = 60 milioni; A ha giocato 5 mila lire quindi gli spettano 5 · 60 milioni; …

Un altro tipo di ripartizione che si presenta frequentemente è rappresentato dal seguente esempio: "per preparare un certo cocktail occorre miscelare 2 parti di liquore A, 3 parti di succo d'arancia e 2 parti di liquore B. Quanto succo d'arancia serve per preparare 50 cl di cocktail?":

n° delle parti di succo 3 succo(in cl)= ——————————————————————— ·50 = ————— ·50 = ... n° totale delle parti 2+3+2

oppure:

50 succo(in cl)= 3· ————— = ... 2+3+2

Un ulteriore esempio di relazione di proporzionalità è quella che interviene nella rappresentazione di dati mediante numeri indici  (non "numeri indice" in "numero indice" la parola "indice" è un aggettivo):
100 numero indice = dato · ————————— dato base
La rappresentazione è ottenuta ponendo uguale a 100 un certo dato di riferimento (dato base) e modificando con lo stesso fattore di proporzionalità gli altri dati. Nel caso dei grafici a lato, relativi ai record di salto in alto maschile e femminile in vigore ogni 4 anni dal 1932 al 1988, se si prende come dato base il record nel 1932 si ottengono i numeri indici rappresentati graficamente sotto:
Ora entrambi i grafici partono dallo stesso punto ed è più facile confrontare i due andamenti e valutare i miglioramenti rispetto alle diverse condizioni di partenza, che sono legate anche ad aspetti fisici (le donne sono mediamente più basse) e sociali (non esistevano gare di atletica femminile fino agli inizi del XX secolo). La trasformazione è avvenuta moltiplicando i record nel caso M per 100/203 (203 è il record maschile nel 1932, la moltiplicazione di 203 per 100/203 lo trasforma in 100), nel caso F per 100/165 (165 è il record femminile nello stesso anno).  Dal 1932 al 1988 il numero indice F è passato da 100 a 127; quindi il record femminile in tale arco di anni è aumentato del 27%. Il numero indice M del 1988 è 120; quindi il record maschile è aumentato del 20%. Anche questa rappresentazione ha tuttavia i suoi limiti.

  Anche i cambiamenti di unità di misura (già considerati sopra ) sono trasformazioni proporzionali.

Ad es. per esprimere 1500 m/min in km/h, posso fare così:

– prima trasformo il rapporto in m/h moltiplicando per 60 (1 h = 60 min quindi passando da "al minuto" a "all'ora" la strada percorsa viene moltiplicata per 60),

– poi trasformo il rapporto in km/h dividendo per 1000 (1 km = 1000 m quindi passando da "metri" a "chilometri" la misura della strada percorsa viene divisa per 1000).

La trasformazione complessiva ("·60" e "/1000) può essere espressa con:

                                             60
  (velocità in km/h) = (velocità in m/min)· ———— =
                                            1000

= (velocità in m/min)· 0.06

Lo stesso si può dire dei cambi di valuta. Ad esempio quando è stato introdotto l'Euro si è posta l'equivalenza  1 Euro = 1936.27 Lire: 1936.27 è il fattore di proporzionalità per trasformare "valori in Euro" in "valori in Lire", 1/1936.27 è quello per trasformare "valori in Lire" in "valori in Euro".     A lato è rappresentata graficamente la trasformazione da euro in lire; si può usare il grafico anche per operare la trasformazione inversa, ad es. per ottenere che 12 mila lire equivalgono a circa 6.2 euro (6 euro e 20 cent.).

  Il coefficiente di proporzionalità non è altro che la pendenza della retta che rappresenta graficamente la relazione di proporzionalità, infatti [  Pendenza ]:

           variazione di y
pendenza = ———————————————
           variazione di x

Vi sono anche coppie di grandezze che, pur non essendo proporzionali, hanno variazioni proporzionali. Ciò accade, per esempio, per la temperatura in °C e la temperatura in °F: il grafico di (temperatura in °F) in funzione di (temperatura in °C), riprodotto a lato, è una retta che non passa per l'origine e che ha pendenza 180/100 = 1.8. Alla variazione di 1°C corrisponde quella di 1.8°F, alla variazione di 3°C corrisponde quella di 3 · 1.8 = 5.4 °F, …
[clicca per ingrandire]→
Per tarare un termometro a gradi Celsius si può associare 0 alla posizione raggiunta dal mercurio quando lo strumento è immerso in acqua fondente (acqua liquida contenente acqua ghiacciata), associare 100 quando è immerso in acqua bollente, e, sulla base di questi due valori, fissare un sistema di riferimento, cioè graduare la colonnina di vetro, in modo da poter associare ad ogni sua posizione un numero (che sarà la temperatura in °C dell'ambiente in cui è posto il termometro, se quella è la posizione raggiunta dal mercurio).     Nel caso di un termometro a gradi Fahrenheit si procede analogamente, associando ai due ambienti (acqua liquida/ghiacciata e acqua bollente) i valori 32 e 212; questa scala consente di rappresentare temperature atmosferiche molto basse con numeri positivi, cosa comoda in regioni particolarmente fredde (ad es. -5°C sono 23°F).     In entrambi i casi le temperature sono ottenute in modo da avere variazioni proporzionali a quelle della lunghezza della colonnina di mercurio; quindi avranno anch'esse variazioni tra loro proporzionali.     Più avanti vedrai che nelle scienze fisiche per la temperatura si usa spesso una diversa scala i cui valori vengono chiamati temeperature assolute (vedi la soluzione dell'esercizio 5.7 qui).

A fianco sono stati riprodotti: • il grafico della relazione di proporzionalità y = x · 2, cioè la retta che passa per (0,0) e ha pendenza 2; • il grafico della relazione y = x · 2 + 3, che ha ancora pendenza 2 (se x varia di 1 allora y varia di 2, se x ha una variazione h allora y ha una variazione pari a h·2) ma che passa per il punto (0,3), e • il grafico della relazione y = x · 2 – 1, che ha ancora pendenza 2 ma che passa per il punto (0,-1).

A fianco è riprodotto il grafico che illustra come sono state determinate le tariffe ferroviarie del 1991 [ Esempio]: fino a 1000 km di percorrenza il prezzo è stato fatto variare proporzionalmente alla percorrenza; oltre si è proseguito con "aumenti" di prezzo proporzionali agli "aumenti" della percorrenza, ma con un fattore di proporzionalità più basso: fino a 1000 km, 60 mila/1000 = 60 lire al km; oltre si ha un aumento di 25 mila/2000 = 12.5 lire al km.

A lato è riprodotto il grafico che corrisponde alle tariffe del 2010, per i viaggi di 2ª classe a prezzo più basso. La forma è del grafico è simile a quella del grafico in vigore un tempo.  Si tratta, tuttavia, di tariffe "virtuali":  esse valgono solo per alcuni treni di breve percorrenza. Per i treni di maggiore percorrenza valgono tariffe molto maggiori, che variano secondo una casistica abbastanza complessa.

I fattori di proporzionalità possono essere anche negativi.     Nel caso illustrato a fianco x e y mantengono la loro somma costantemente uguale a 10, per cui ad ogni aumento di x corrisponde un'uguale diminuzione di y, ossia a ogni variazione di x corrisponde una variazione di y opposta (uguale in valore assoluto e di segno diverso). Il rapporto tra la variazione di y e quella di x è quindi –1.     A questa relazione corrisponde graficamente una retta con pendenza –1.     Quando si parla di grandezze proporzionali spesso si sottointende che il fattore di proporzionalità sia positivo.

 Note.
•  Quando due grandezze non costanti G₁ e G₂, in un certo contesto, sono legate da una relazione di proporzionalità, ossia quando esiste un numero k diverso da 0 tale che G₂ = G₁·k, si usa anche scrivere G₂ ∝ G₁, dove il simbolo ∝ si legge "è proporzionale a".  Le due grandezze, a seconda dei contesti, possono variare solo sui numeri nonnegativi (come a volta accade in fisica), su tutti i numeri reali o su intervalli particolari (ad esempio l'allungamento di una molla può essere proporzionale alla massa ad essa sospesa solo fino ad un certo valore, oltre il quale la molla perde elasticità).

•  Quando i numeri  a, b, c, d, … sono trasformati proporzionalmente, mediante una moltiplicazione per un numero k diverso da 0, nei numeri  a', b', c', d', … (a' = a·k, b' = b·k, …), si dice che la sequenza  a', b', c', d', …  è proporzionale alla sequenza  a, b, c, d, …. Possiamo scrivere (a', b', c', d', …) ∝ (a, b, c, d, …).
Un tempo era diffusa la scrittura  a' : b' : c' : d' : … = a : b : c : d : …, in cui il simbolo di divisione ":" è usato con un significato che coincide con l'usuale se le sequenze sono composte da due soli numeri, non se sono tre o più.  Ad es. 10:2:5 = 20:4:10 è vera se interpretata come (10,2,5) ∝ (20,4,10) (una sequenza è ottenibile dall'altra moltiplicandone gli elementi per 2), non se interpretata come sequenza di divisioni: 10:2:5 = (10:2):5 = 5:5 = 1; 20:4:10 = (20:4):10 = 5:10 = 0.5 ≠ 1).

Esercizi:       [esercizi più semplici: ]

 altri collegamenti     [nuova pagina]