Prospettiva

  L'illusione della profondità

Voglio rappresentare due palle di dimensioni diverse che sono poste una più lontana dell'altra.
    Se faccio il disegno (0) non riesco a far comprendere quale delle due sia più vicina, e non riesco nemmeno a far capire che si tratta di due palle invece che di due dischi.
    Se, come in (1), sovrappongo le figure, faccio percepire quale dei due oggetti è più vicino e, più in generale, creo una senzazione di profondità.
    In (2) per creare questa sensazione si è ricorsi a variazioni del colore, per dare l'illusione di oggetti tridimensionali colpiti dalla luce proveniente da una particolare sorgente luminosa, e a smorzamenti dei contorni di ciò che si vuol far apparire più lontano.
    Un altro metodo per dare idea della profondità è, nel caso di oggetti più o meno della stessa grandezza, diminuire le dimensioni di quelli che si vogliono far sembrare più lontani; questa è la tecnica adottata in (3).

(0)

(1)

(2)

(3)

(4)

Quest'ultima tecnica, applicata alla rappresentazione di un binario, dà luogo a una figura come (4): il fatto che le traversine debbano apparire man mano più piccole fa sì che i due binari, che sono paralleli, debbano essere rappresentati lungo due direzioni diverse, ossia con due tratti rettilinei che, prolungati, convergano in un punto (senza poterlo scavalcare, altrimenti le traversine ricomincerebbero ad aumentare di dimensione).     Questo accorgimento (rappresentare linee parallele che si allontanano facendole convergere in un punto) può essere usato in molte altre situazioni. Ne abbiamo già accennato in un punto precedente ( proiezioni tra superfici).

(5)

Ecco un altro esempio: la rappresentazione di una scatola cubica di materiale trasparente. Gli spigoli a, b, c e d, che - vedi (5) - sono tra loro paralleli, li rappresento lungo rette che si incontrano nello stesso punto. Gli spigoli perpendicolari al mio sguardo, che stanno su rette che non si allontanano, li disegno mantenendoli paralleli. Gli spigoli verticali, poiché sto guardando dall'alto, li disegno lungo linee che tendono a convergere, lentamente, in un punto in basso.     In (6) la rappresentazione di un cerchio (potrebbe essere l'orlo di un vaso): lo immagino inscritto in un quadrato, disegno come vedrei il quadrato e, poi, traccio la figura che rappresenta il cerchio (il centro del cerchio non è più al centro, ma è più vicino alla parte più lontana del bordo).

(6)

  Punti di fuga. Orizzonte.

    La rappresentazione piana (su un foglio o su altro materiale) di oggetti tridimensionali viene chiamata prospettiva. Qui abbiamo incominciato a considerare alcune tecniche prospettiche. I punti verso cui tendono a convergere le rappresentazioni di traiettorie parallele, come il punto P nella figura (5), vengono detti punti di fuga: sono i punti verso cui si "fugge" se ci si muove lungo queste traiettorie. In altre parole, il punto di fuga della rappresentazione di una retta è il limite a cui tende la rappresentazione di un punto che si muove allontanandosi lungo tale retta.
    Queste prime tecniche sono sufficienti per affrontare approssimativamente solo alcuni disegni. Se volessimo realizzare un disegno come il seguente (una casetta vicina a una linea ferroviaria) avremmo il problema di dove collocare i diversi punti di fuga corrispondenti alle diverse direzioni lungo cui sono diposti, per es., gli spigoli della casa e del tetto e i binari. Poi ci sarebbero anche problemi relativi alle dimensioni e alle distanze; ad es. la distanza tra le traversine, che nella realtà è costante, come farla variare man mano che ci si allontana lungo i binari?

(7)

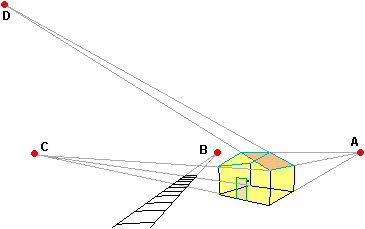Affrontiamo una prima questione. Nel disegno i punti di fuga A, B e C sono tutti allineati: stanno su una stessa retta orizzontale. Se casa e binario fossero su una grande pianura, questa linea coinciderebbe con la linea che, ai nostri occhi, separerebbe terra e cielo. È il cosidetto orizzonte. Le figure seguenti ci consentono di capire meglio questo fenomeno.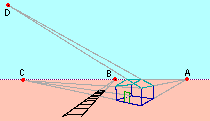

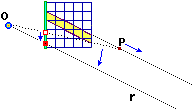
    Voglio disegnare una tovaglia a quadretti con una banda gialla posta su un tavolo quadrato. Per fare il disegno utilizzo una lastra di plastica trasparente collocata verticalmente su uno dei bordi del tavolo e osservo la tovaglia attraverso la lastra con un solo occhio, O, nel modo illustrato sotto a sinistra. Al centro si vede quello che vedo. Con un pennarello traccio ciò che vedo sulla lastra: in pratica la lastra è la finestra da cui guardo la scena, ovvero è il quadro su cui rappresento la scena. Ogni punto tracciato con il pennarello in corrispondenza di un punto della tovaglia non è altro che l'intersezione con la lastra del raggio visivo che congiunge il mio occhio con tale punto: vedi figura a destra, in cui la cosa è evidenziata per i due vertici posteriori del tavolo.

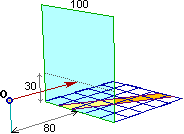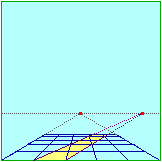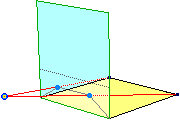    Nella figura sopra al centro è visualizzato anche il fatto che se col pennarello prolungo le immagini dei bordi laterali della tovaglia o di quelli della banda, essi vanno a confluire su punti di fuga che stanno su una linea del quadro (ossia della lastra) che è alla stessa altezza del mio occhio (vedi figura sopra a sinistra). La figura in basso a sinistra spiega questo fenomeno: se un punto si allontana lungo il piano del tavolo, il raggio visivo che collega il mio occhio ad esso tende a diventare orizzontale, e l'intersezione di questo raggio con la lastra tende a stabilizzarsi alla stessa altezza del mio occhio.

    Il fenomeno è più generale, come mette in luce la figura sopra a destra: se un punto P si allontana stando su un piano orizzontale (ossia perpendicolare alla finestra attraverso cui guardo la scena e parallelo alla base), alla mia vista esso tende a stabilizzarsi sulla linea individuata sulla finestra dal piano orizzontale π che passa per il mio occhio O. Questa linea è l'orizzonte (relativo a questa finestra e a questa posizione dell'occhio).

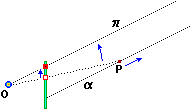La cosa non accade solo per i piani orizzontali. Se un punto P si allontana lungo un piano α, alla mia vista esso tende a stabilizzarsi sulla linea individuata sulla finestra dal piano π parallelo ad α che passa per il mio occhio O. Tutte le rette che stanno su α (e non sono parallele alla finestra) hanno punti di fuga che stanno su questa linea.

Tornando alla scena con casa e ferrovia, i lati di base della casa e del tetto, lo spigolo superiore del tetto e i binari hanno punti di fuga sull'orizzonte. Lo spigolo superiore del tetto sta sull'orizzonte; ciò significa che l'occhio sta alla stessa altezza del tetto.     A, E e D sono punti di fuga di rette che stanno sul piano di una delle facce del tetto; sono allineati, ma non sull'orizzonte in quanto non si tratta di un piano parallelo al piano orizzontale.  Qui puoi vedere (variando il punto di vista) la casetta a lato e i punti all'infinito.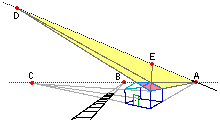

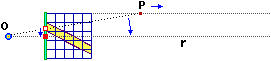
  Le figure sottostanti, che mostramo dall'alto la persona che sta osservando la tovaglia, spiegano perchè rette parallele vengono viste confluire nello stesso punto:  a sinistra si vede un punto che si allontana perpendicolarmente alla finestra e tende, sul quadro, a stabilizzarsi di fronte al mio occhio;  a destra si vede che le rette dirette come i bordi della banda gialla tendono a confluire tutte in un altro punto dell'orizzonte, il punto intersecato sul quadro dalla retta passante per l'occhio e diretta come i bordi della banda.

  Descrivendo le tecniche del disegno spesso si usano notazioni e denominazioni particolari. Facendo riferimento alle figure sottostanti, q è il "quadro", V è il "centro di vista" (l'occhio), h è la distanza tra centro di vista e piano orizzontale, f è la "fondamentale" (retta in cui si intersecano piano orizzontale e quadro), O è l'"orizzonte", V₀ è il "punto di fuga principale", D₁ e D₂ sono i "punti di fuga diagonali". Questi ultimi sono i punti verso cui l'osservatore vede convergere le rette orizzontali inclinate di 45° rispetto al quadro; sono detti anche "punti di distanza", perché, come si vede nella figura a destra, la loro distanza da V₀ è pari alla distanza dell'osservatore dal quadro; essi, su un quadro, consentono di valutare la distanza che avrebbe l'osservatore.

  Come si modificano le distanze.

    Le considerazioni svolte ci aiutano a schizzare facilmente un paesaggio come quello considerato in figura (7): si traccia una retta e si tracciano in modo che confluiscano in un punto di essa i due lati di base opposti della casa e i corrispondenti lati superiori, si fanno confluire in un altro punto gli altri due lati e …; in un altro punto si fanno confluire i binari; …. In modo analogo si può realizzare la rappresentazione di un oggetto astratto, come un cubo.

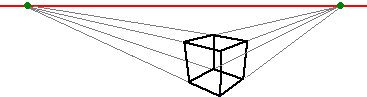
    Utilizzando opportunamente intersezioni tra rette dirette verso il punto di fuga principale e i punti di fuga diagonali a cui abbiamo accennato nel punto precedente si può in alcuni casi anche stabilire con quali distanze tra loro rappresentare su un quadro i diversi oggetti.
    Vediamo, su un esempio, un metodo più generale. Ad esempio, nel caso sotto raffigurato, dell'occhio posto a distanza 0.3 (in qualche unità di misura fissata) dal piano in cui stanno gli oggetti e a distanza 0.8 dal quadro, un oggetto collocato in A, a una distanza 0.2 dal quadro, a che distanza dalla base del quadro dovrò rappresentarlo? Ossia, KP quanto vale?
    I triangoli HAO e KAP sono simili, per cui KP/KA = HO/HA, ossia KP/0.2 = 0.3/1, ossia KP = 0.3·0.2 = 0.06.
    Analogamente B lo rappresento a una distanza KQ dalla base tale che KQ/KB = HO/HB, ossia KQ/1 = 0.3/1.8, ossia KQ = 0.3/1.8 = 0.166…

  L'analisi delle seguente foto, del Loggiato Maggiore del Palazzo Ducale di Genova, realizzata con una buona macchina fotografica, avvalora il procedimento descritto nei punti precedenti.
    Rette parallele tra loro (e non al quadro) vengono viste confluire in uno stesso punto: la balaustra e la sua ombra convergono verso il punto D, le rette che congiungono la base inferiore del blocco su cui poggia una colonna con la base superiore di quello successivo convergono verso il punto E, le ombre di pilastrini e colonne convergono vero il punto A, il lato del porticato perpendicolare a quello visto in primo piano e la linea perpendicolare alla balaustra che separa due tipi di pavimentazione convergono verso B, …
    Le rette che stanno su piani orizzontali (ombre di colonne, balaustre, profili del tetto, …) convergono tutti sulla stessa retta, AD.
    Le rette che stanno sul piano delle colonne o su piani ad esso paralleli (come il lato opposto del porticato) convergono sulla stessa retta, DF.

    Il punto G è quello in cui convergono le rette che congiungono gli elementi reali con le loro ombre: è la posizione del sole. I raggi del sole arrivano sulla terra praticamente paralleli, quindi G è pensabile anche come il punto di fuga di segmenti paralleli diretti come i raggi del sole.

Si noti che l'analisi geometrico-prospettica della foto consente di capire che la Torre Grimaldina, che si vede sullo sfondo, non ha facce parallele ai lati del loggiato, come potrebbe suggerire una osservazione superficiale della foto soprastante (diversamente da quanto accade con la foto qui a destra). Infatti, altrimenti, il bordo superiore della faccia in primo piano dovrebbe stare su una retta che passa per il punto D.

    Flash nella storia dell'arte

[clicca sulle immagini per ingrandimenti]

L'ultima cena (Duccio di Boninsegna, 1310 circa)
Prime avvisaglie della prospettiva:
Gli elementi del cassettone al centro del soffitto hanno un unico punto di fuga. Gli elementi degli altri cassettoni convergono sull'asse di simmetria. Altri elementi del dipinto (come le strisce sulla tovaglia, che sono perpendicolari al quadro come gli elementi del cassettone) non convergono.

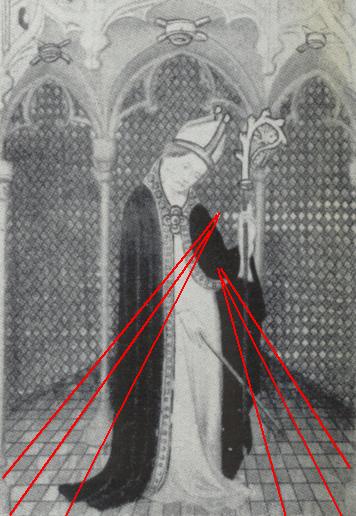
Le difficoltà a volte vengono superate ricorrendo a "trucchi" quali coprire con personaggi, vesti o festoni le parti del dipinto in cui la prospettiva risulta più difficile, come nel caso di questo dipinto della fine del XIV secolo, in cui il personaggio copre la parte in cui vanno a confluire le rappresentazioni delle file di piastrelle.

San Sebastiano (Antonello da Messina, 1476) Padronanza della prospettiva ormai raggiunta:
	Il punto di vista viene scelto drammaticamente basso. Come si può stimare usando le considerazioni svolte sopra, o come si può individuare simulando la visione con un opportuno programma (vedi la figura a destra, ottenuta con R), l'occhio è posto a circa 5 m da S. Sebastiano e a circa 30 cm da terra (la finestra è verticale, ovvero, considerando lo sguardo diretto perpendicolarmente alla finestra, il punto mirato è sul santo alla stessa altezza da terra).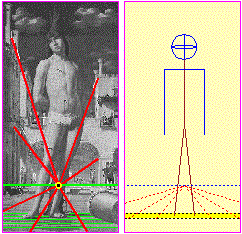
	A sinistra è riprodotto uno studio sulla rappresentazione prospettica di un pentagono regolare ad opera di Piero della Francesca (1412-1492), che ha elaborato una delle prime trattazioni matematiche della prospettiva.

Due disegni (ingrandibili con un clic) tratti da manuali di pittura (dei primi anni del '500) del pittore tedesco Albrecht Dürer che spiegano, a sinistra, la prospettiva come intersezione tra raggi visivi e quadro, e, a destra, come realizzare un disegno in prospettiva utilizzando un reticolo quadrettato collocato verticalmente e un foglio quadrettato (su cui riportare l'immagine vista attraverso il reticolo).

Giochi di bimbi, visione parziale (Pieter Breughel, 1560, pittore olandese)

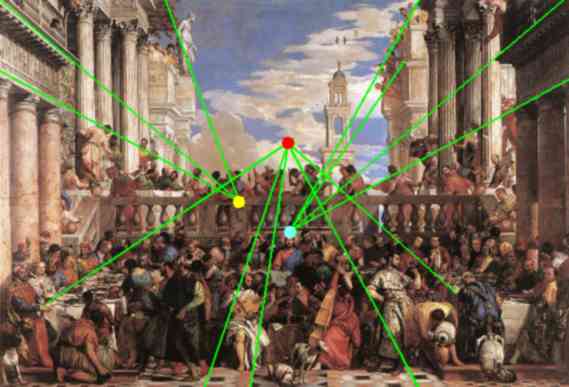
Le nozze di Cana (Il Veronese, 1563)
Sicura padronanza della prospettiva, e suo superamento:
Scelta consapevole di più punti di fuga (qui ne sono evidenziati alcuni), per mettere in risalto i diversi elementi e dare più respiro alla scena (sono compresenti ben 7 punti di vista).

Con Picasso e il cubismo viene superato l'obiettivo di rappresentare illusionisticamente la profondità. La superficie del quadro è uno spazio in cui viene organizzata una scomposizione/ricostruzione intellettuale della realtà; entra in gioco anche una quarta dimensione, mentale (e temporale): le figure non sono rappresentate da un unico punto di vista, ma contemporaneamente come le si vedrebbero in diverse posizioni (dell'osservatore e/o dei soggetti), con nasi di profilo su volti frontali, occhi ad altezze diverse, testa e tronco orientati diversamente, …. [ipertesto con approfondimenti sulla prospettiva nell'arte]

Les demoiselles d Avignon (Picasso, 1907)

    Paradossi della visione

Il nostro apparato visivo (occhio+cervello), grazie a forme di elaborazione in parte congenite e in parte sviluppate attraverso l'esperienza, è in grado di interpretare come immagine 3D (a 3 dimensioni) l'immagine 2D (a 2 dimensioni) che arriva sulla retina. Potremmo dire che abbiamo "incoporato" qualche procedimento matematico che ci consente ciò. Questo nostro "vedere non solo con gli occhi" è anche uno dei fattori di un particolare tipo di illusioni ottiche, chiamate paradossi della visione.     Si consideri ad es. la figura a fianco. È costituita dall'unione di tre parallelogrammi, ma alla nostra vista sembra che il lato più alto del parallelogramma più grande sia più lungo del lato opposto. Ciò accade in quanto il nostro occhio interpreta la figura come l'immagine 2D di un oggetto 3D e quindi tende a percepire il lato "lontano" come più lungo, per compensare l'effetto prospettico, sopra discusso, della riduzione degli oggetti più lontani.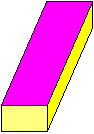

A destra à illustrato un altro fenomeno:  un ambiente è deformato in modo da produrre la stessa immagine di una camera normale; l'uomo che appare piccolo in realtà è alto come l'altro uomo, ma è piazzato più lontano. La forma della stanza (chiamata "camera di Ames"), e la collocazione del punto di vista, sono stali da dare l'impressione che si tratti di ambiente a forma di parallelepideo rettangolo. Nel disegno A' rappresenta l'interperatazione della collocazione che dà l'osservazione dell'uomo a sinistra, che in realtà è posto in A.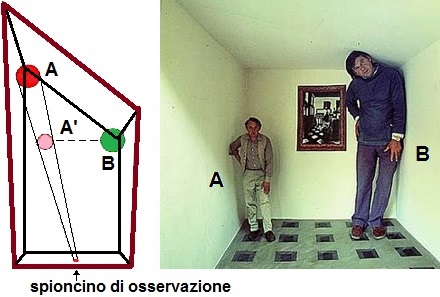

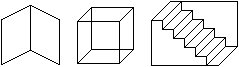Nel caso delle figure soprastanti tendiamo a parcepirle come rappresentazioni di oggetti tridimensionali a noi noti (un libro aperto, un cubo, delle scale), ma la loro errata prospettiva (lati vicini e lontani sono rappresentati nelle stesse dimensioni) ci crea ambiguità interpretativa, se non un vero e proprio distrurbo fisico: se fissiamo gli oggetti dopo un po' ci appaiono diversi, e poi la nostra impressione cambia ancora. Non riusciamo a fissare quali componenti sono da intendere in primo piano e quali in secondo. Solo aggiungendo dei colori o dei particolari, come sotto, riusciamo a sciogliere l'ambiguità.

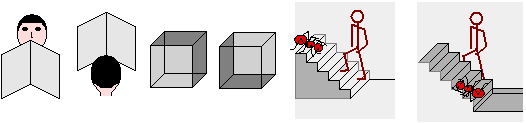	Anche la figura a destra rappresenta una scala, ma qui l'ambiguità è diversa: non è tra vicino e lontano come accadeva per la scala di sopra (che, a seconda di che cosa si interpretava come "muro", portava a intendere la scala come vista dall'alto o dal basso), ma è legata al fatto che vengono unite due figure che corrispondono a punti di vista diversi: è la vista globale della figura che ci disturba; se ne copriamo la parte superiore o inferiore il conflitto sparisce.
Qualcosa di simile accade per la figura sopra a sinistra: se mettiamo a fuoco la parte destra della figura vediamo un coniglio; se mettiamo a fuoco quella sinistra vediamo un'anatra.
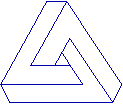
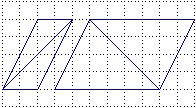
	Anche la figura a destra (nota come "triangolo impossibile") ci crea un distrurbo visivo solo se la guardiamo globalmente, in tutti i suoi vertici: è l'unione di 3 figure fatte a "7", ma ci richiama l'idea della rappresentazione piana di un solido che non riusciamo a interpretare.     La figura a sinistra mette in luce altri limiti della nostra intuizione spaziale: due segmenti uguali, formati ciascuno da 4 diagonali di quadretto, a prima vista ci sembrano diversi.

Questo fenomeno in parte può essere interpretato, come si è fatto per la prima figura, in relazione a un tentativo di interpretazione 3D, in parte in relazione ad altri problemi percettivi, legati alla contemporanea presenza di parti di figura disposte diversamente o colorate diversamente, che ci fanno apparire segmenti uguali come diversi, rette parallele come incidenti, line rette come incurvate, rettangoli come figure non rettangolari, esemplificabili con le immagini seguenti (nell'ultima vediamo dei pallini grigi che in realtà non esistono).

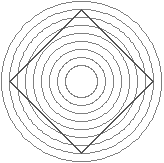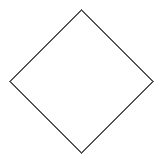
Di questi aspetti non ci occupiamo.     Più avanti ci occuperemo invece di alcuni problemi più specifici, come quello illustrato dalla figura a lato.     Guardo una figura tracciata sul terreno da una distanza di circa 20 m e da un'altezza iniziale di 2 m. Vicino alla figura è collocato un sistema di "assi" di riferimento, con assi finiti (lunghi 10 m ciascuno). La figura sembra un arco di ellisse. Ma man mano che mi alzo (l'altezza passa da 2 m a 60 m) la figura mi appare come una parabola.     È possibile che una parabola venga vista come un'ellisse?     Oltre ai "paradossi della visione", in matematica si considerano paradossi di altro genere: vedi qui.

    QUI puoi esercitarti col computer (viene aperta una nuova finestra in cui puoi osservare una casetta da diversi punti di vista).
    Per ottenere rappresentazioni tridimensionali, in qualunque sistema operativo, puoi usare R; qualche esempio lo trovi qui e qui.  Clicca per vedere/studiare una figura simile a quella considerata alla fine del precedente paragrafo. Clicca per avere una vista animata di una figura simile.
[Se stai lavorando da un computer che ha Windows come sistema operativo, puoi usare anche il programma per rappresentazioni tridimensionali che puoi aprire cliccando qui sia per rivedere, in modo operativo, gli argomenti affrontati, sia per avere un'idea di come si possono realizzare le rappresentazioni prospettiche al computer (qui hai un help ed esempi)]

Esercizi:    

 altri collegamenti     [nuova pagina]