Prospettiva 2

  Riepilogo

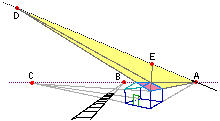
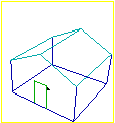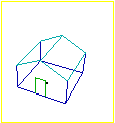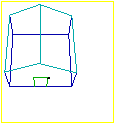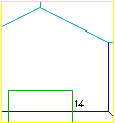
Alla voce  prospettiva 1 abbiamo visto come rappresentare una scena come quella a fianco (una casetta vicina a una linea ferroviaria):  i lati di base della casa e del tetto, lo spigolo superiore del tetto e i binari hanno punti di fuga sull'orizzonte. Lo spigolo superiore del tetto sta sull'orizzonte; ciò significa che l'occhio sta alla stessa altezza del tetto.     A, E e D sono punti di fuga di rette che stanno sul piano di una delle facce del tetto; sono allineati, ma non sull'orizzonte in quanto non si tratta di un piano parallelo al piano orizzontale.     Abbiamo anche visto alcuni aspetti della storia dell'arte legati a questo tema (alcuni di essi sono approfonditi in uno specifico ipertesto).

	A sinistra è richiamata, dalla voce  prospettiva 1, una finestra in cui puoi osservare la casetta considerata nella figura precedente da diversi punti di vista.
	Nella stessa voce abbiamo, poi, preannunciato che ci saremmo occupati di alcuni problemi più specifici, come quello illustrato dalla figura a lato, che qui riprendiamo:
«Guardo una figura tracciata sul terreno da una distanza di circa 20 m e da un'altezza iniziale di 2 m. Vicino alla figura è collocato un sistema di "assi" di riferimento, con assi finiti (lunghi 10 m ciascuno). La figura sembra un arco di ellisse. Ma man mano che mi alzo (l'altezza passa da 2 m a 60 m) la figura mi appare come una parabola.  È possibile che una parabola venga vista come un'ellisse?»     Affrontiamo, dunque, questo problema.

  Ancora sulle proiezioni

	Sopra abbiamo visto come una parabola, vista dal basso, possa apparire un'ellisse.  La figura a lato illustra come mezza iperbole, collocata nel piano xy ed avente gli assi x ed y come asintoti (anche in questo caso raffigurati parzialmente), man mano che il mio sguardo si dirige più orizzontalmente tende ad assumere forma ellittica, fino a che (figura D), quando lo sguardo è diretto parallelamente alla sua bisettrice, si presenta al mio sguardo proprio come una semiellisse (e gli assi x ed y mi appaiono come rette tra loro parallele).
	A destra è illustrata la direzione dello sgaurdo nella situazione D.     Come è possibile ciò?  Proviamo a dare una risposta.

Se  clicchi qui accedi ad una visione animata di quel che accade tagliando un cono circolare retto (avente come asse di simmetria l'asse z) con un piano con inclinazione rispetto al piano z = 0 maggiore, minore od uguale a quella delle generatrici del cono (dicesi generatrice una retta che passa per il vertice del cono e sta sulla sua superficie, la cui rotazione attorno all'asse del cono genera il cono stesso).  Puoi studiare meglio il fenomeno azionando la animazione "coniche", o quella illustrata a fianco: vedi.     Sotto, a sinistra, una sintesi della animazione:  se taglio il cono con un piano, non passante per il suo vertice, inclinato come una generatrice ottengo una parabola; se il piano è inclinato di più o di meno ottengo un'iperbole o un'ellisse.  Se guardo queste intersezioni dal vertice del cono, dirigendo lo sguardo come l'asse di rotazione, le vedo tutte circolari o, meglio, come un cerchio (l'ellisse) o un cerchio bucato (la parabola) o un arco di cerchio (l'iperbole); vedi figure sotto a destra.  Questa semplice spiegazione risolve le apparenti contraddizioni generate dalle immagini precedenti.

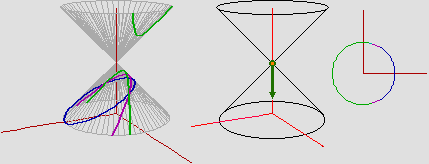
    Il fatto che ellissi, iperboli e parabole ( figure 2) possono essere ottenute dalla intersezione di un cono con un piano è all'origine del fatto che tali curve vengono chiamate, complessivamente, coniche.

    Quanto ora detto permette di concludere anche che ( proiezioni tra superfici) le coniche sono ottenibili l'una dall'altra mediante una proiezione centrale, e che quindi sono indistinguibili dal punto di vista delle proprietà proiettive.

    Le coniche possono essere tutte ottenute, nel piano xy, come grafico di una equazione polinomiale di 2° grado, ossia di un'equazione in x ed y del tipo  ax² + bxy + cy² + dx + ey + f = 0 (affinché sia di 2° grado occorre che a, b e c non siano tutti nulli).
    Un'equazione di questo genere ha alcuni casi "degeneri": casi in cui non ha "punti" (x,y) che la risolvono (ad es. x²+y²+1=0), o ha per soluzione solo un punto (ad es. x²+y²=0, soddisfatta solo se x=0 e y=0) o una retta (ad es. (x−y)²=0, soddisfatta solo se y=x) o una coppia di rette (ad es. x²−y²=0, soddisfatta solo se y=x o y=−x).  Negli altri casi rappresenta un'ellisse, un'iperbole o una parabola.
    Si può dimostrare che la classificazione in queste tre categorie dipende solo dai valori di a, b e c. Vediamo la casistica:
• se  b²−4ac = 0  (ad es. (x−2y)²+3y−4=0) è una parabola,
• se  b²−4ac > 0  (ad es. (x−y)(x+2y)+3y−4=0) è una iperbole,
• se  b²−4ac < 0  (ad es. 0.5x²+y²+3y−4=0) è una ellisse.
    Ecco, in ordine, i grafici dei tre esempi fatti sopra, tra parentesi:

    Qui trovi come fare i grafici delle coniche precedenti, e come studiarle, con R.  Qui puoi trovare qualche approfondimento sulle coniche.  [vedi anche l'esercizio 7a.13]

  Rappresentazione matriciale

Facciamo qualche cenno a come, mediante le matrici, è possibile unificare lo studio della trasformazioni affini e proiettive. Abbiamo visto che, se il numero complesso z0 ha la forma polare (ρ, α), z → z·z0 equivale a una rotazione attorno a (0,0) ampia α composta con una omotetia di fattore ρ ( numeri complessi).  Da qui si ricava facilmente che una rotazione di ampiezza α del punto (x,y) è ottenibile col prodotto di matrici indicato a lato ( matrici).  Qui trovi un esempio realizzato con R.

cos(α)   −sin(α)    ×    x    sin(α)    cos(α) y

1   0    ×    x   0   7 y

Anche le funzioni scala e le simmetrie ( trasformazioni geometriche) sono facilmente interpretabili matricialmente.  Ad es. a lato è considerata la dilatazione verticale x' = x + 0y = x, y' = 0x + 7y = 7y.

La matrice a destra rappresenta invece la simmetria "obliqua" rispetto all'asse x e parallela alla retta y = hx (ombra proiettata da raggi diretti come y = hx):  x' = x − 2hy, y' = −y  ( proiezioni tra superfici).

1    −2h   0    −1

1   tan(α)   0     1

Invece la matrice qui a sinistra rappresenta un inclinamento di α nella direzione dell'asse x ( calcolatore 5).

    Per comporre trasformazioni di questo genere si possono moltiplicare le rispettive matrici (infatti il prodotto tra matrici è associativo). Quindi se voglio sottoporre una figura a una sequenza di trasformazioni basta che calcoli una volta per tutte la matrice prodotto e la moltiplichi via via per i vettori colonna che rappresentano i punti della figura.
    Componendo trasformazioni di questi tipi (ne basterebbero solo alcuni, in quanto altri sarebbero ottenibili per composizione dagli altri), ovvero moltiplicando matrici di questi tipi, si ottengono tutte le possibili trasformazioni rappresentabili in uno dei due modi seguenti, dove la matrice 2×2 è ad elementi in R e non ha righe (ovvero colonne) tra loro proporzionali.

x'   =    a   b    ×    x   y' c   d y

x' = ax + by y' = cx + dy

x' = ax + by + h y' = cx + dy + k

Se aggiungiamo la possibilità di comporre traslazioni abbiamo, al variare di a, b, c, d, h e k in R – con (a,b) non proporzionale a (c,d), e, quindi, con (a,c) non proporzionale a (b,d) – abbiamo tutte le affinità ( proiezioni tra superfici), ossia le proiezioni parallele, eventualmente composte con un ingrandimento/riduzione di scala.  Ma le traslazioni non sono descrivibili matricialmente nel modo precedente: moltiplicando una matrice per il vettore (x,y) non posso ottenere coefficienti senza x o y.

    Per estendere i vantaggi della rappresentazione matriciale alle traslazioni si possono introdurre le coordinate omogenee. Se rappresento (x,y) come terna (x,y,1) posso rappresentare le traslazioni nel modo indicato sotto a sinistra, le affinità che mandano l'origine in sé stessa nel modo indicato sotto al centro;  facendo il prodotto di due matrici che rappresentano queste trasformazioni – nel modo indicato sotto a destra – ottengo la rappresentazione matriciale di una generica affinità:

1   0   h    ×    x    =    x+h   0   1   k y y+k 0   0   1 1   1

a   b   0    ×    x    =    ax + by   c   d   0 y cx + dy 0   0   1 1     1

1   0   h    ×    a   b   0    =    a   b   h   0   1   k c   d   0 c   d   k 0   0   1 0   0   1 0   0   1

In pratica ho rappresentato ogni punto del piano (x,y) con il punto (x,y,1) del piano z = 1, come illustrato nella figura a destra (che puoi cliccare per vederla più grande). La retta (0,0,0)-(x,y,1) rappresenta il raggio visivo con cui da (0,0,0) vedo il punto (x,y) del piano di quota 1.  Sono coordinate omogenee anche quelle aventi come terza componente un qualunque numero k diverso da 0: basta prendere il punto di intersezione del precedente raggio visivo con tale piano; ad esempio (3,5,1) posso considerarlo equivalente a (6,10,2), a (1,5/3,1/3) o a (3k,5k,k), con k≠0.     Vediamo come, in generale, viene trasformata una conica, con i punti rappresentati in tal modo, mediante una matrice che non abbia necessariamente i primi due elementi dell'ultima riga eguali a 0:
a11  a12  a13    ×    x    =    a11 x + a12 y + a13   a21  a22  a23 y a21 x + a22 y + a23 a31  a32  a33 1 a31 x + a32 y + a33
Riduco l'elemento sull'ultima riga ad 1:
(a11 x + a12 y + a13) / (a31 x + a32 y + a33)   (a21 x + a22 y + a23) / (a31 x + a32 y + a33) 1

    Dunque ((a₁₁ x + a₁₂ y + a₁₃) / (a₃₁ x + a₃₂ y + a₃₃), (a₂₁ x + a₂₂ y + a₂₃) / (a₃₁ x + a₃₂ y + a₃₃)) è il trasformato, mediante la matrice, di (x, y). È facile verificare che una conica  ax²+ bxy + cy²+ dx + ey + f = 0  mediante una trasformazione di questo tipo rimane una conica.

Ad esempio il cerchio  x2 + y2 = 1  trasformato mediante la matrice rappresentata a destra diventa la curva di equazione  (x − y + 1)2/(x + y + 1)2 + (x + y + 2)2/(x + y + 1)2 = 1, cioè (2x2 + 6x + 2y2 + 2y + 5) / (x + y + 1)2 = 1, ossia la parabola  x2 + y2 − 2xy + 4x + 4 = 0.  Sotto, sullo stesso sistema di riferimento, sono rappresentati sia la conica iniziale (in blu) che la sua trasformata (in rosso):		1  –1   1   1    1   2 1    1   1

I punti (0, −1) e (−1, 0) del cerchio (quelli in cui si annulla x+y+1) non vengono trasformati in un punto della parabola: questa matrice trasforma il cerchio in una parabola, e quindi devono esservi dei punti del cerchio avvicinandosi ai quali i loro trasformati tendono ad avere coordinate infinite.

In verde è rappresentata la trasformazione dello stesso cerchio mediante la matrice rappresentata a destra; l'equazione diventa  (2x2 + 6x + 2y2 + 2y + 5) / (x − 2y + 1)2 = 1, ossia  x2 − 2y2 + 4xy + 4x + 6y + 4 = 0.  In questo caso si tratta di una iperbole. I punti (−1,0) e (0.6,0.8) del cerchio (quelli in cui si annulla x−2y+1) non vengono trasformati in punti: man mano che ci si avvicina ad essi sul cerchio nell'iperbole ci si allontana dal "centro" di essa, in una delle direzione degli asintoti.

1  –1   1   1    1   2 1  –2   1

    Per "sistemare le cose" le inclinazioni delle rette vengono chiamati punti impropri (o all'infinito).  In questo modo tutte le trasformazioni rappresentabili in questo modo mediante matrici trasformano punti in punti, e si può effettuare uno studio opportunamente unificato di esse.  Si intuiscono i collegamenti del concetto di punto improprio con quello di punto di fuga. Ma qui ci fermiamo, rinviando ad eventuali successivi studi l'approfondimento di questi argomenti. Facciamo, solo, ancora un cenno ad alcune terminologie.

  Assonometrie

La illustrazione a lato richiama un altro tipo di rappresentazione, studiato a scuola nelle materie grafiche:  le assonometrie.  Una assonometria non è altro che una proiezione parallela ( proiezioni tra superfici).     Sotto, il piano z = 4 è rappresentato sia in prospettiva centrale (a sinistra) che con una assonometria.  A destra è descritta la trasformazione da R3 in R2 che corrisponde a questo tipo particolare di assonometrie (man mano che avanzo di 1 nella direzione x, nella immagine bidimensionale retrocedo di h nella direzione y e di k nella direzione z).     Una assonometria in cui, come in questa, il piano su cui avviene la proiezione (u,v) è parallelo ad uno dei piani del sistema di riferimento (y,z) viene detta assonometria cavaliera.

Le proiezioni parallele sono casi limite delle proiezioni centrali, come si vede nell'illustrazione seguente, in cui man mano l'occhio O viene allontanato sempre più dal punto mirato M.  Anche questo lo avevamo già osservato alla voce  proiezioni tra superfici.

Esercizi:    

 altri collegamenti     [nuova pagina]