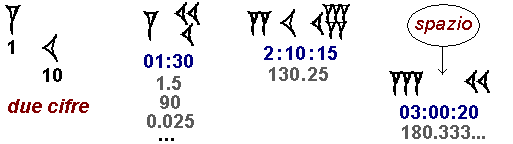
La numerazione babilonese
Noi indichiamo i tempi con una notazione ibrida.
Usiamo come simboli le cifre decimali, ma le usiamo per formare numeri con cui poi indichiamo multipli o sottomultipli non di tipo decimale
(come decimi, centesimi, decine o centinaia) ma di tipo diverso.
Ad esempio
In breve, per i tempi espressi in ore, minuti e secondi si usa una "base sessanta", le cui "cifre" sono composte impiegando le cifre decimali. Per i giorni si usa una base 24, mentre le frazioni di secondo le esprimiamo in centesimi.
Si intrecciano, quindi, una base 60, una base 24 e una base 100 (a cui, a volte, con l'impiego aggiuntivo di attributi come P.M. e A.M., si affianca il ricorso a una base 12).
I Babilonesi, già intorno al 1800 a.C., scrivevano i numeri con una notazione sessagesimale simile a quella che noi impieghiamo per indicare ore, minuti e secondi. Usavano, però, per indicare le "cifre" sessagesimali (quelle che noi indichiamo con 00, 01, …, 58, 59, impiegando le cifre decimali), solo 2 cifre, fatte a forma di chiodo: un chiodo verticale, che corrisponde al nostro 1, e un punzone (cioè un chiodo tozzo) disposto orizzontalmente, che corrsiponde al nostro 10.
Osserva la figura che segue.
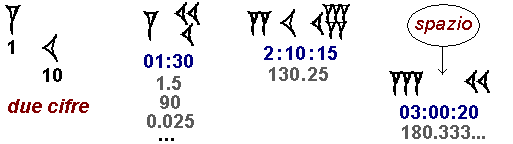
Il nostro 1.5 dai babilonesi era rappresentato con un chiodo seguito da un gruppo di 3 punzoni, con una scrittura simile a quella (01:30) con cui noi indichiamo 1 ora e mezza o 1 minuto e mezzo. Al posto del ":", per distinguere le cifre di multipli o sottomultipli, usavano raggruppare chiodi o punzoni che andavano considerati assieme.
Come facciamo noi con i tempi (che a seconda dei casi scriviamo 01:30 per indicare 1 ora e mezza o 1 minuto e mezzo), usavano la stessa scrittura per indicare numeri con ordini di grandezza diversi. Quindi allo stesso modo in cui indicavano il nostro 1.5 (1:30) indicavano anche 90 (60·1+30), 0.025 (1/60+30/60/60 = 1/120+2/120 = 3/120 = 1/40 = 1/4/10 = 0.25/10), ….
Non avevano però la nostra cifra "zero", che scrivendo i tempi in base 60, di solito indichiamo con 00. Al posto di 00 usavano uno spazio, ma questo creava qualche problema in quanto non era facile capire quanti erano i "posti" da saltare.
Ad esempio nella figura di sopra abbiamo rappresentato 180 e 1/3: 3 chiodi per indicare 3·60, uno spazio per indicare che non ci sono unità e 2 punzioni per indicare che ci sono 20 sessantesimi, ossia 1/3. Se avessimo voluto rappresentare 10800 ( = 60·60·3) e 1/3 avremmo dovuto mettere 3 chiodi, due spazi e 2 punzioni, ottenendo una espressione non facile da distinguere dalla precedente. Intorno al 300 a.C. i Babilonesi superarono questo problema usando al posto dello spazio un chiodo inclinato. 180.333… e 10800.333… diventarono:

La tavoletta sotto riportata rappresenta il valore della lunghezza della diagonale di un quadrato di lato 30. Noi sappiamo che la diagonale di un quadrato di lato 1 è lunga √2 = 1.41421356…, e che quella di un quadrato di lato 30 è 30·√2. Il numero indicato sulla tavoletta lungo la diagonale orizzontale del quadrato in base dieci diventa 1+24/60+51/60^2+10/60^3 = 1.41421296…, la migliore approssimazione di √2 con 4 cifre in base 60 (1+24/60+51/60^2+11/60^3 vale infatti 1.41421759…). Il numero indicato sotto al precedente è il prodotto di esso per 30.
| tavoletta babilonese in argilla 1800-1600 a.C. |
 |

I Babilonesi conoscevano comunque anche la proprietà nota come "teorema di Pitagora", almeno 1000 anni prima di Pitagora (vedi anche la figura A), come calcolare le relazioni tra lati ed angoli dei triangoli rettangoli (come è documentato nei reperti riprodotti nella figura B) e avevano la padronanza dei numeri negativi (come è documentato nei reperti riprodotti nella figura C, anche se solo chi padroneggia la scrittura dei babilonesi è in grado di interpretarli). Ovviamente erano in grado di descrivere anche algoritmi per eseguire questi calcoli. Risalgono ai Babilonesi (attualmente) le prime documentazioni di una descrizione di un procedimento di calcolo.
È sopravvissuto ai nostri giorni l'uso della rappresentazione sessagesimale per le misure degli angoli, anch'esso risalente ai Babilonesi: si divide il cerchio in 360 gradi, ogni grado (°) si suddivide in 60 primi ed ogni primo in 60 secondi. In questo modo è comodo per rappresentare angoli di uso comune: l'angolo retto, pari ad un quarto di giro, misura 90°, un terzo di angolo retto misura 30°, un terzo di giro misura 120°.
| Anche gli antichi Egizi, sicuramente già intorno al 1650 a.C., possedevano un sistema di scrittura dei numeri molto più avanzato di quello adottato secoli dopo dai Greci. Ecco a lato come esprimevano il numero che noi scriviamo 1264. Era una numerazione decimale, in cui utilizzavano simboli per le potenze di 10; ma per scrivere gli altri numeri utilizzavano una scrittura "additiva", ossia ripetevano più volte i simboli delle potenze di 10. A differenza dei Babilonesi non possedevano un metodo comodo per scrivere i numeri più piccoli di 1: utilizzavano frazioni unitarie, ossia del tipo 1/N (che scrivevano utilizzano delle tacche sotto una specie di bocca) e, ad esempio per scrivere 7/12, lo esprimevano come 1/3+1/4 (1/3 = 4/12, 1/4 = 3/12, 1/3+1/4 = 7/12) usando la scrittura illustrata a fianco. |  |
Per dare un'idea della scrittura dei Greci e dei Romani vediamo come scrivevano lo stesso numero considerato sopra, 1264. I Greci (che svilupparono molto gli studi geometrici "astratti") erano molto arretrati nelle applicazioni della matematica e, in particolare, nella "artimetica pratica", in quanto la classe dirigente si occupava solo della cultura "disinteressata", lasciando alle classi subalterne le applicazioni pratiche. In particolare per i numeri usavano un sistema arretratissimo: indicavano, in ordine, con le lettere dell'alfabeto i numeri da 1 a 10 (α, β, …), poi quelli da 20 a 100 (κ, λ, …), poi quelli da 200 a 900 (da σ, τ, …); 1000, 2000, … li indicavano ,α (α preceduta da una specie di virgola), ,β, … Quindi 1264 veniva scritto ",ασξδ". I Romani, sviluppando il sistema di numerazione impiegato dagli Etruschi, scrivevano 1264 nella forma MCCLXIV (come puoi verificare col software R battendo "as.roman(1264)" o con WolframAlpha battendo "1264 as Roman"): mille + cento + cento + cinquanta + dieci + quattro (scritto come "5 meno 1").
Altri commenti:  alla voce rappresentazione sessagesimale dei numeri
alla voce rappresentazione sessagesimale dei numeri