Lo spazio

  Nella vita quotidiana usiamo la parola "spazio" in vari modi: «in fondo alla pagina c'è ancora spazio per tre righe di testo», «ci sono molte stelle nello spazio», «in "lazia" manca uno spazio tra "la" e "zia"», … .
    Potremmo dire che viene utilizzata per indicare un "vuoto" o un "contenitore", di dimensioni prefissate o no, in cui si possono mettere o si può pensare di mettere cose o in cui possono muoversi cose.
    È una descrizione un po' generica del significato di "spazio", e che fa riferimento al significato di altre parole ("vuoto", "contenitore", "cosa", …) il cui significato a sua volta non è semplice descrivere in modo preciso. Non risulterebbe difficile delimitare meglio il significato che assume in alcuni usi particolari (ad es. nel caso dello spazio che manca tra "la" e "zia"), ma non è possibile definire chiaramente il significato più generale di "spazio", neanche ricorrendo a un dizionario.
    Tuttavia attraverso l'uso della lingua italiana, attraverso la memorizzazione di situazioni a cui viene applicata la parola "spazio", … ci costruiamo mentalmente un significato di spazio che è sufficiente per l'usuale comunicazione linguistica.

    Anche in matematica la parola "spazio" viene usata in modi diversi, per indicare vari concetti. Ma, per salvaguardare la natura astratta dei modelli matematici [  modello ], questi concetti non possono essere descritti riferendosi solo a specifiche applicazioni pratiche e al significato intuitivo di parole d'uso quotidiano.
    Vediamo alcuni esempi.

  Voglio caratterizzare matematicamente le posizioni lungo una traiettoria "rettilinea", concetto intuitivo di cui abbiamo come prototipo un raggio di luce, la traiettoria di un sasso lasciato cadere da una certa altezza, un filo teso, il segno tracciato con una matita appoggiata a una riga, … (ricorrere a questi esempi è sufficiente per chiarire il significato di "rettilineo" nel linguaggio comune).

Posso allora considerare lo spazio costituito dalla retta dei numeri, che non è altro che la struttura dei numeri reali dotata della relazione d'ordine "<":
chiamo punti i numeri reali e segmenti gli intervalli di numeri reali, e, se x<y, dico che il punto x precede il punto y nella direzione positiva o che y precede x nella direzione negativa.	il punto –2.4 precede/segue il punto 0.8 rispetto alla direzione positiva/negativa

    Posso arricchire questo modello di spazio dotandolo della  distanza d così definita:
            d(x, y) = | x – y |.
    La distanza tra i due punti considerati nella figura è | –2.4 – 0.8 | = | – 3.2 | = 3.2.

    "Concretamente", la retta dei numeri viene rappresentata con un tratto rettilineo (cioè tracciato con un riga) sul quale sono state segnate almeno due tacche a cui siano stati associati due numeri.
    I numeri associati ad altre posizioni sono individuati (approssimativamente) in modo che la distanza fisica (misurata con uno strumento) tra posizioni sia proporzionale alla distanza matematica tra i punti-numeri corrispondenti.

Ad esempio se segno una tacca 0 e una tacca 2 a 15 mm di distanza, il punto 1 starà a metà strada, a 7.5 mm sia da 0 che da 1; il punto 2.8 starà a 2.8·7.5 = 21 mm dal punto 0 e (poiché 2.8 = 2+0.8) a 0.8·7.5 = 6 mm dal punto 2.

    Così come i  numeri reali sono un modello astratto delle misure di grandezze, così questi punti sono un'astrazione delle posizioni lungo una "retta concreta", le quali, nella realtà, non possono essere stabilite "esattamente".

  Come modello matematico per caratterizzare posizioni "esatte" su una superficie piatta (di cui abbiamo come prototipi la parte superiore di un tavolo, una piazza senza rilievi o affossamenti e con il fondo liscio, la parete di un muro, la superficie di uno stagno, …), generalizzando l'uso delle coordinate nelle carte geografiche, posso considerare le coppie (x,y) di numeri reali.
    L'insieme di queste coppie viene chiamato piano numerico o piano cartesiano o, più semplicemente piano.
[l'aggettivo "cartesiano" deriva da Descartes, latinizzato in Cartesius, nome di un grande studioso francese - che si occupava di filosofia, scienze, matematica - vissuto nel 17° secolo che è tra coloro che hanno introdotto e sviluppato l'uso di numeri ed equazioni numeriche per descrivere le figure geometriche]

    Per rappresentare "concretamente" il piano si usa il procedimento che abbiamo già descritto per i grafici delle funzioni a 1 input e 1 output [ diagrammi].

    Anche il piano numerico può essere dotato di una  distanza

La retta numerica e il piano cartesiano sono, rispettivamente, uno spazio monodimensionale (a 1 dimensione) e uno spazio bidimensionale (a 2 dimensioni), in quanto i rispettivi punti sono individuati, rispettivamente, da 1 numero e da 2 numeri. Tali numeri vengono detti coordinate.     Per indicare posizioni che non stanno su una traiettoria rettilinea o su una superficie piana (ad esempio la posizione di un aereo o di un sommergibile) dobbiamo ricorrere a tre coordinate, cioè considerare lo spazio tridimensionale costituito dalle terne (x,y,z) di numeri reali:  nella figura a lato il punto A ha (x,y) = (4,3) e quota  z = 1.

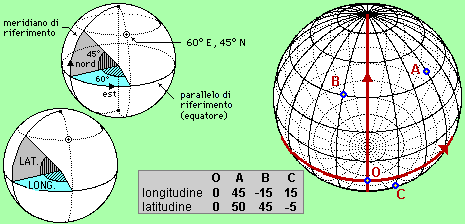
  Le posizioni su una superficie sferica, ad esempio sulla superficie terrestre, possono, invece, essere individuate mediante due numeri reali (coordinate geografiche), da –180 a 180 (la longitudine, o azimut) e da –90 a 90 (la latitudine).     Questo è uno spazio bidimensionale.

Il diagramma a lato rappresenta i millimetri di pioggia mensili nel corso di tre anni; il cerchio con raggio minore rappresenta 50 mm di pioggia; quello con raggio maggiore rappresenta 150 mm di pioggia; le semirette disposte a raggera rappresentano i mesi. Il diagramma consente di analizzare l'evoluzione del fenomeno e, insieme, di confrontarne gli andamenti in tre anni successivi (si vede che i mesi estivi sono diventati più piovosi, che in primavera la piovosià ha sempre oscillato intorno ai 100 mm/mese di pioggia, …). Un diagramma di questo tipo si chiama polare in quanto ha un aspetto simile alla visione dall'alto di un polo circondato dai paralleli e attraversato dai meridiani. Con un metodo simile è possibile anche individuare un qualunque punto del piano: basta indicarne la distanza e la direzione in cui muoversi dal polo per raggiungerlo. Ad esempio il pallino che rappresenta il primo dato ha distanza 41 dal polo e è nella direzione 30° (misurata a partire dalla semiretta evidenziata). Questi due numeri vengono chiamati coordinate polari del punto. Le coordinate usuali, quando si voglia chiarire che non ci si rifersce a quelle polari, vengono chiamate cartesiane. Qui puoi vedere come ottenere un diagramma in coordinate polari con R.

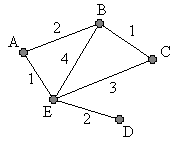Per un altro esempio si pensi alla situazione illustrata dal grafo a fianco, in cui i nodi rappresentano località, gli archi rappresentano strade (a doppio senso) e i numeri le lunghezze (in km) di queste.     Anche questo modello matematico può essere considerato uno spazio: possiamo chiamare punti i nodi del grafo e distanza tra x e y la lunghezza del percorso più breve per andare da x a y.

Volendo fare a meno della rappresentazione con pallini e linee posso descrivere questo spazio come l'insieme che ha per elementi A, B, C, D ed E ed è dotato della funzione distanza definita dalla tabella a fianco.     Per quanto riguarda in particolare il piano cartesiano in altre sezioni si vede come si possono descrivere altre  figure e  trasformazioni a cui possono essere soggette le figure del piano (traslazioni, rotazioni, ingrandimenti, dilatazioni, …).

x  y  A   B   C   D   E  A  0 2 3 3 1 B  2 0 1 5 3 C  3 1 0 5 3 D  3 5 5 0 2 E  1 3 3 2 0

  Nota 1.   I termini orizzontale e verticale in matematica spesso sono usati in modo convenzionale, come fatto sopra. In altri casi (e in particolare in fisica) sono usati in un modo diverso: verticale indica "diretto come la forza di gravità", ossia come il filo a piombo, mentre orizzontale indica "perpendicolare alla direzione verticale". Dunque, nel caso ci si restringa ad un piano che passa per la verticale, l'orizzontalità indica una direzione (che varia man mano che ci si sposta su un'altra verticale), mentre nel caso tridimensionale l'orizzontalità indica un piano (che varia man mano che ci si sposta su un'altra verticale). A volte l'orizzontalità viene riferita a una superficie: una superficie orizzontale è una superficie che, in ogni suo punto, è perpendicolare alla verticale passante per quel punto. Nel caso della Terra, una superficie orizzontale è pressoché sferica (ma, se ci occupiamo di una zona molto limitata, possiamo, anche in fisica, supporre che si tratti di un piano).

  Nota 2.   Per indicare che un punto P e un punto Q, ad esempio dello spazio bidimensionale, hanno coordinate (5, 3) e (2,−3) si può scrivere P = (5, 3) e Q = (2,−3).  È sbagliato  scrivere, anche se si trova su vari libri di testo scolastici, che i punti sono P(5, 3) e Q(2,−3). Una lettera seguita da una parentesi, infatti, indica una funzione.  In qualche manuale di geometria si usa, effettivamente, il simbolo di funzione P per associare ad una generica coppia di coordinate (h,k) il punto P(h,k), ma lo si usa per ogni coppia di coordinate:  i punti di coordiante (5, 3) e (2,−3) in questo caso vengono indicati P(5, 3) e P(2,−3).  Lo "sbaglio", ovviamente, non è tanto dal punto di vista "tecnico" (se si mettono delle avvertenze sulla notazione che si sta usando), ma dal punto di vista "culturale": non costa niente mettere un "=" per evitare il sorgere di misconcezioni; un tempo, ovviamente, quando non esiteva la notazione F(x) per indicare l'output di x mediante la funzione F, questo problema non esisteva (ma è un tempo "lontano": questa notazione è stata introdotta nella prima metà del XVIII secolo; ed è stato "breve": l'uso delle coordinate era stato introdotto un solo secolo prima).

Esercizi:  testo  e  soluzione,   testo  e  soluzione,   testo  e  soluzione.

 altri collegamenti     [nuova pagina]