Struttura di un termine

  Con struttura di un termine [ formule] si intende il modo in cui esso viene costruito a partire dagli atomi, cioè dalle variabili e dalle costanti che compaiono in esso.

Ad es. √2 +	A·B	e  √A +	B·5	sono termini diversi ma con la stessa struttura.
	——		——
	C		3

I  grafi ad albero seguenti descrivono i due termini evidenziandone la struttura comune; il nodo iniziale, "+", rappresenta l'operazione principale: si tratta di termini che sono ottenuti mediante l'addizione di altri termini:

+ _____/ \______ SQR / | ____/ \____ 2 * C __/ \__ A B

+ _____/ \______ SQR / | ____/ \____ A * 3 __/ \__ B 5

SQR indica la radice quadrata, * indica la moltiplicazione
[come nei linguaggi di programmazione Basic]

    I termini man mano ottenuti costruendo un termine si chiamano sottotermini di esso.

Ad es. √2 +  A·B  ha come sottotermini: —— C •  gli atomi 2,  A,  B  e  C, cioč i nodi finali del grafo ( figura a fianco), e •  √2,  A·B  e  A·B , —— C cioè i termini che hanno come operazione principale quella rappresentata nei nodi intermedi ( figure sottostanti).

+ ___/ \___ SQR / | ___/ \___ 2 * C __/ \__ A B

+ ___/ \___ SQR / | ___/ \___ 2 * C __/ \__ A B		+ ___/ \___ SQR / | ___/ \___ 2 * C __/ \__ A B		+ ___/ \___ SQR / | ___/ \___ 2 * C __/ \__ A B
radice quadrata		moltiplicazione		divisione

  I termini possono essere scritti in modi diversi.
    Ad esempio il termine precedente può essere scritto anche √2 + ((A·B)/C) o, usando le usuali convenzioni (richiamate sotto) sulla priorità delle operazioni, √2 + A·B/C.

Convenzioni:  un termine in cui compaiano più simboli di operazione e non compaiano parentesi è da intendersi come "abbreviazione" del termine ottenuto aggiungendo parentesi in questo modo: (a)  si considerano i simboli di operazione nell'ordine di priorità (1) "^", (2) "·" e "/", (3) "–" (negazione), (4) "+" e "–" (sottrazione),  e per ciascuno di essi si introducono parentesi in modo che esso leghi i più piccoli sottotermini adiacenti; (b)  nel caso si succedano due simboli con la stessa priorità viene considerato prima quello a sinistra. Ad es. 5+2/3 sta per 5+(2/3) in quanto "/" lega più di "+"; analogamente 4^2/5 sta per (4^2)/5 e –3^2, ovvero –32, sta per –(3^2), ovvero –(32).  8–3–2 sta per (8–3)–2 in quanto il "–" a sinistra lega di più.
• La scrittura delle divisioni nella forma "a più piani" è una abbreviazione per eliminare eventuali parentesi dal primo e dal secondo termine e dall'intera divisione; ad esempio  1 / ((2+3)/7)  può essere riscritto nel modo illustrato a destra. Nel caso di più linee di divisione, quelle più corte legano più delle altre; ad es. il termine rappresentato all'estrema destra abbrevia ((4+7)/5)/6.	4+7    2+3   ———  1:———    5     7   —————           6
• Si noti che (23)4 equivale a (2^3)^4, mentre il termine rappresentato a destra spesso è interpretato come 2^(3^4). Per evitare ambiguità, nel caso di scritture di potenze che impieghino più di 2 piani conviene usare parentesi per indicare le priorità ed evitare scritture come quella a destra; nel caso specifico per intendere 2^(3^4) occorrerebbe usare come esponente (34). Per altro, nel caso di "^" la convenzione (b) di associare a sinistra non è accettata da tutti i software: alcuni interpretano 2^3^4 come (2^3)^4, altri come 2^(3^4). In questi casi per evitare confusioni è bene non eliminare mai le parentesi.	4      3     2
• Si osservi che l'operazione "principale" di un termine è quella che lega meno, ossia quella che ha "priorità" inferiore.

Vi sono anche convenzioni che consentono di omettere il simbolo di moltiplicazione:
• 2(x+3)  e  (a+b)(1+c)  stanno per  2·(x+3)  e  (a+b)·(1+c), ossia lo si può omettere quando il secondo termine della moltiplicazione è racchiuso tra parentesi;
• πR ,  Rπ  e  5x  stanno per  π·R,  R·π  e  5·x, ossia lo si può omettere quando è chiaro dal contesto che sono moltiplicati due simboli di costante o di variabile; in casi particolari, in cui si faccia la convenzione di indicare le variabili con singole lettere e mai non con nomi formati da più lettere, si può scrivere anche bc (con un piccolo spazio in mezzo) al posto di  b·c  (in qualche manuale di Fisica viene usata la, strana, convenzione di interpretare 1/2x, con 2 appiccicato ad x, come 1/(2·x), diversamente da 1/2 x che viene interpretato come (1/2)·x).

Le parentesi non servono se si descrive un termine mediante un grafo ad albero. Nella scrittura usuale sono invece indispensabili. Le coppie di parentesi più interne, come si è visto sopra, indicano calcoli che sono "prioritari", cioè che corrispondono a parti più basse del grafo ad albero. Spesso si usano coppie di parentesi di dimensioni o forme diverse per facilitare la lettura di un termine, ma forma e dimensione delle parentesi non indicano alcuna priorità, che è espressa solo dalla collocazione delle parentesi stesse (se in qualche libro hai letto di priorità tra parentesi tonde, quadre e graffe, scordatele: sono solo sciocchezze). Le parentesi, in matematica, sono usate anche con altri significati, che scoprirai man mano.

Qui, nel punto (03), trovi come esercitarti sull'uso dei grafi ad albero di termini con R.

  È molto importante saper analizzare la struttura dei termini. Serve per:

•  calcolare seguendo un ordine corretto il valore di un termine numerico, interpretare il significato di una formula, costruire una formula che rappresenti un certo procedimento di calcolo;

•  fare correttamente  trasformazioni di termini/formule in termini/formule equivalenti;

•  descrivere un termine in un linguaggio diverso: impostarne il calcolo su una CT, descriverlo in un linguaggio di programmazione o in un programma per il calcolo simbolico.

+ ___/ \___ 7 / ___/ \___ – 2 __/ \__ 9 4

Ad es.  7 +  9 − 4   non posso tradurlo come —— 2              7 9 4 2 che invece corrisponde a  7 + 9 −  4 — 2     Se la CT ha i tasti di parentesi posso invece battere prima di 9 e dopo di 4, per far sí che come primo termine della divisione venga preso  9 – 4, non solo 4.

Altrimenti posso usare:		9 4 2 7
o trasformare  7 +  9 − 4   nel termine   9 − 4  + 7 —— —— 2 2
ad esso equivalente e battere:		9 4 2 7

  Quando si manipola un termine in genere se ne cambia la struttura. Vediamo un esempio riferito alla applicazione della regola di riscrittura [ ternini equivalenti]  a·(b+c+…) a·b+a·c+… per distribuire il fattore moltiplicativo a tra i termini di una sequenza di addizioni, cioè per portarlo dentro al sottotermine (b+c+…):  4·157 = 4·(150+7) = 4·150+4·7 = 600+28 = 628

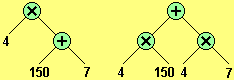Nel passaggio da 4·(150+7) a 4·150+4·7 la struttura del termine è cambiata nel modo raffigurato a fianco: l'operazione "principale" non è più la moltiplicazione, ma la addizione, cioè il termine si presenta come una somma di termini invece che come un prodotto di termini.

  La struttura di un termine può essere descritta anche elencando le operazioni che vi compaiono nell'ordine in cui vanno eseguite. Questo è, essenzialmente, ciò che fa un programma traduttore [ calcolatore 2] quando trasforma un'assegnazione in una sequenza di istruzioni in linguaggio macchina.

Ecco come viene trasformata l'assegnazione (scritta in un linguaggio Basic) corrispondente alla formula a fianco:

3 2 ·-x w = ——————— + x·5 9 - 1

ASSEGNAZIONE: W = (2^3*-X)/(9-1)+X*5 variabili->REGISTRI: R0 = (2^3*-R1)/(9-1)+R1*5 + Traduzione in _________/ \_________ istruzioni elementari: / * R2 = 2 ^ 3 _____/ \_____ ____/ \____ R3 = - R1 * - X 5 R4 = R2 * R3 __/ \__ __/ \__ R5 = 9 - 1 ^ - 9 1 Grafo ad albero R6 = R4 / R5 / \ | corrispondente R7 = R1 * 5 2 3 X R0 = R6 + R7

    Ecco i passaggi con cui da tale grafo si può risalire alla scrittura nel linguaggio di programmazione, partendo dai nodi a sinistra in basso:

2^3 2^3*–x (2^3*–x)/(9-1) (2^3*–x)/(9-1)+x*5

    Qui  e  qui  trovi vari esercizi di questo tipo.

[ Se vuoi, in R puoi "caricare" la "libreria" codetools che contiene il comando showTree(quote(...)) che fornisce in ordine l'operazione principale e le operazioni via via secondarie, come si leggono sul grafo ad albero precedente ("tree" significa "albero"):

library(codetools)
showTree(quote(  (2^3*-x)/(9-1)+x*5  )) 
(+ (/ ("(" (* (^ 2 3) (- x))) ("(" (- 9 1))) (* x 5))
Le scritte "(" segnalano solo la presenza di più parentesi, con la
la possibiità di trasformare le "((...))" in "(...)", come se fosse:
(+ (/ ((* (^ 2 3) (- x))) ((- 9 1))) (* x 5))
(+ (/ (* (^ 2 3) (- x)) (- 9 1)) (* x 5))
ovvero in questo modo:
walkCode(quote(  (1^2*-3)/(4-5)+6*7  ))
`+`
`/`
`(`
`*`
`^`
[1] 1
[1] 2
`-`
[1] 3
`(`
`-`
[1] 4
[1] 5
`*`
[1] 6
[1] 7
Le '(' indicano solo l'avvio di una sottodiramazione;
per questo non ci sono le ')'.
Come trasformare quanto sopra nel grafo seguente:

Se vuoi, se sei in ambiente Windows, cliccando QUI, puoi attivare il programma Compilazione (o il più semplice programma Albero) che realizza e visualizza trasformazioni e grafi come nell'esempio precedente (per avviare il programma, dalla finestra di dialogo che si apre scegli "Apri", non "Salva").  Puoi trovare anche un programma per calcolare termini numerici in cui devi man mano introdurre numeri e funzioni in ordine di composizione, nella cosiddetta notazione postfissa, con la quale il termine descritto sopra viene introdotto come:   2 3 ^ x - * 9 1 _ / x 5 * +   in un modo che corrisponde alla lettura del grafo a partire da sinistra, leggendo ogni nodo dopo (il o) i due rami che partono da esso; per la negazione e la sottrazione si devono usare due simboli diversi.  QUI trovi un semplice script per calcolare termini numerici descritti in notazione postfissa (vedi anche gli esempi).]

Esercizi:

 altri collegamenti     [nuova pagina]