Termini equivalenti
 Due termini vengono detti algebricamente equivalenti quando assumono gli stessi valori, cioè: comunque sostituisco valori alle eventuali variabili che compaiono in essi, ottengo due termini che sono entrambi definiti o entrambi indefiniti e, nel primo caso, hanno lo stesso valore.
Due termini vengono detti algebricamente equivalenti quando assumono gli stessi valori, cioè: comunque sostituisco valori alle eventuali variabili che compaiono in essi, ottengo due termini che sono entrambi definiti o entrambi indefiniti e, nel primo caso, hanno lo stesso valore.
 Ad esempio a+b+c può essere riscritto nella forma: c+a+b o nella forma: b+(c+a). Con qualche calcolo a mano su alcuni esempi numerici è facile convincersi che i nuovi termini sono algebricamente equivalenti al termine originale:
Ad esempio a+b+c può essere riscritto nella forma: c+a+b o nella forma: b+(c+a). Con qualche calcolo a mano su alcuni esempi numerici è facile convincersi che i nuovi termini sono algebricamente equivalenti al termine originale:
| 2+3+9 = 5+9 = 14 | |
9+2+3 = 11+3 = 14 | |
3+(9+2) = 3+11 = 14 | |
| 8+7+2 = 15+2 = 17 | |
2+8+7 = 10+7 = 17 | |
7+(2+8) = 7+10 = 17 | |
La dimostrazione che ciò valga in generale è molto complicata.
Possiamo convincerci di questa equivalenza interpretando "fisicamente" la addizione:
se cambio l'ordine con cui congiungo tre aste non cambia la lunghezza dell'oggetto che ottengo.

Con un analogo ragionamento "fisico" posso convincermi che equivalenze simili valgono anche nel caso di una quantità diversa di addizioni, cioè che in generale vale la cosiddetta proprietà del riordino della somma:
due termini ottenuti entrambi applicando ripetutamente l'addizione a partire dagli stessi sottotermini t1, t2, …, tn sono termini equivalenti.
 Analogamente, interpretando la moltiplicazione come modello matematico per il calcolo dell'estensione di una superficie rettangolare, posso convincermi del fatto che: Analogamente, interpretando la moltiplicazione come modello matematico per il calcolo dell'estensione di una superficie rettangolare, posso convincermi del fatto che:
a·d+b·d+c·d equivale a (a+b+c)·d | 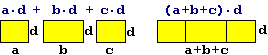 |
e più in generale del fatto che:
a(b + c + …) = ab + ac + … e (b + c + …)a = ba + ca + …
cioè che vale la cosiddetta proprietà distributiva
della moltiplicazione rispetto alla addizione. |
 Ad essere rigorosi, ricorrere a queste spiegazioni "fisiche" è un po' un cane che si morde la coda: le operazioni aritmetiche sono state inventate per affrontare più facilmente problemi relativi a grandezze fisiche, economiche, …; non possiamo capovolgere la situazione e dedurre certe proprietà delle operazioni aritmetiche dal fatto che, operando concretamente con grandezze fisiche, con valori monetari, … si verificano certi fatti.
Ad essere rigorosi, ricorrere a queste spiegazioni "fisiche" è un po' un cane che si morde la coda: le operazioni aritmetiche sono state inventate per affrontare più facilmente problemi relativi a grandezze fisiche, economiche, …; non possiamo capovolgere la situazione e dedurre certe proprietà delle operazioni aritmetiche dal fatto che, operando concretamente con grandezze fisiche, con valori monetari, … si verificano certi fatti.
È un "circolo vizioso" anche verificare alcune proprietà di base (la possibilità di riordinare un'addizione, di raccogliere a fattor comune, …) facendo un po' di calcoli (a mano o con la CT) su alcuni esempi numerici. Infatti nell'esecuzione dei calcoli, spesso senza che ce ne accorgiamo, vengono già usate queste proprietà.
Ad esempio consideriamo l'esecuzione a mano di 24·32: troviamo 48 facendo 24·2, troviamo 720 mettendo uno zero finale e facendo 24·3, sommiamo 48 e 720. Nel far ciò abbiamo trasformato 24·32 in 24·2+24·3·10:
24·32 → 24·(2+30) → 24·2+24·30 → 24·2+24·(3·10) →
24·2+24·3·10 | 24 x
32 =
————
24·2 —> 48 +
24·30 —> 720 =
————
768 |
Comunque, poichè non possiamo porci l'obiettivo di dimostrare tutto (a scuola non si può riinventare in pochi anni tutta la matematica che è stata messa a punto in millenni, né la scuola pre-universitaria ha l'obiettivo di formare dei "piccoli matematici"!), confidando sul fatto che le operazioni aritmetiche e gli algoritmi di calcolo usuali siano stati definiti bene, a volte ricorreremo ad esemplificazioni di tipo fisico o a esperimenti numerici per giustificare alcune proprietà.
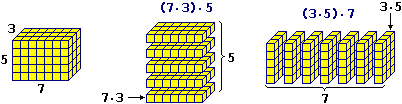
 Con ragionamenti fisici ed esperimenti numerici (ad es. osservando che per contare i cubetti della figura seguente posso sia sommare 5 strati di 7·3 cubetti, cioè fare 7·3·5, che sommare 7 strati di 3·5 cubetti, cioè fare 3·5·7) possiamo convincerci che vale anche la proprietà del riordino del prodotto:
Con ragionamenti fisici ed esperimenti numerici (ad es. osservando che per contare i cubetti della figura seguente posso sia sommare 5 strati di 7·3 cubetti, cioè fare 7·3·5, che sommare 7 strati di 3·5 cubetti, cioè fare 3·5·7) possiamo convincerci che vale anche la proprietà del riordino del prodotto:
due termini ottenuti entrambi applicando ripetutamente la moltiplicazione a partire dagli stessi sottotermini t1, t2, …, tn sono termini equivalenti.
 Per calcolare 17+29+13·118 con una CT senza priorità conviene considerare 13·118+17+29. Il nuovo termine è equivalente al termine iniziale in base alla proprietà del riordino della somma.
Per calcolare 17+29+13·118 con una CT senza priorità conviene considerare 13·118+17+29. Il nuovo termine è equivalente al termine iniziale in base alla proprietà del riordino della somma.
Per precisare in che modo è stato riordinato il termine possiamo dire che abbiamo applicato la regola di riscrittura a+b+c → c+a+b (a è 17, b è 29, c è 13·118). Si è già usata questa notazione alla voce  formule.
formule.
La direzione della freccia indica il verso in cui viene effettuata la sostituzione.
A volte la stessa riscrittura viene indicata con a+b+c ← c+a+b (qui la freccia è alla rovescia: indica che l'espressione a destra "subentra" al posto di quella a sinistra) o con a+b+c = c+a+b o con a+b+c := c+a+b.
Nota 1. Parlando di "applicare regole" non si vuol dire che, nel calcolo algebrico, ci sono procedimenti standard per i diversi tipi di problemi a cui occorre attenersi. Stiamo usando la parola "regola" per indicare uno schema, una descrizione sintetica di una particolare trasformazione, fra le varie che possono essere scelte e combinate per risolvere un certo problema.
 È utile, soprattutto finché si è dei "principianti", svolgere i calcoli di tipo algebrico provando a esplicitare (a parole o con una regola di riscrittura), ogni volta che si fa un passo durante la trasformazione di un termine, il procedimento che si è impiegato. Questo aiuta a controllare se sono presenti errori. Si rallenta un po' la velocità di calcolo, ma questa non è la cosa più importante: l'importante è non commettere errori.
È utile, soprattutto finché si è dei "principianti", svolgere i calcoli di tipo algebrico provando a esplicitare (a parole o con una regola di riscrittura), ogni volta che si fa un passo durante la trasformazione di un termine, il procedimento che si è impiegato. Questo aiuta a controllare se sono presenti errori. Si rallenta un po' la velocità di calcolo, ma questa non è la cosa più importante: l'importante è non commettere errori.
In caso di incertezza (nel trovare il procedimento da usare o nel controllo della regola scelta o della sua applicazione) può essere utile fare qualche esempio numerico o pensare a qualche situazione d'uso, di tipo geometrico-fisico (come visto sopra) o di altro genere: ad es. il ricordo che premendo 2 volte  sul visore ricompare il numero di partenza può suggerire la regola 1/(1/a) → a.
sul visore ricompare il numero di partenza può suggerire la regola 1/(1/a) → a.
Del resto, ai nostri giorni, anche i calcoli simbolici vengono svolti utilizzando opportuni programmi al calcolatore. Ciò che occorre è scrivere i termini correttamente (cioè seguendo il linguaggio - convenzioni, simboli, … - utilizzato dal programma che si impiega) e dare man mano i comandi giusti per effettuare le trasformazioni che ci interessano. E per entrambe queste cose occorre avere chiara la  struttura del termine su cui si opera e saper individuare le
struttura del termine su cui si opera e saper individuare le  regole di riscrittura che si vogliono applicare.
regole di riscrittura che si vogliono applicare.
 Riepiloghiamo le più comuni "regole di riscrittura" che si possono applicare per trasformare termini in termini ad essi algebricamente equivalenti, indicando anche il modo in cui vengono in genere descritte verbalmente, dai matematici e nelle applicazioni di calcolo simbolico. Su altri aspetti del calcolo algebrico si torna in altre voci [risoluzione di equazioni, di sistemi, …]. Tieni conto che:
Riepiloghiamo le più comuni "regole di riscrittura" che si possono applicare per trasformare termini in termini ad essi algebricamente equivalenti, indicando anche il modo in cui vengono in genere descritte verbalmente, dai matematici e nelle applicazioni di calcolo simbolico. Su altri aspetti del calcolo algebrico si torna in altre voci [risoluzione di equazioni, di sistemi, …]. Tieni conto che:
• nelle regole riportate nei riquadri le lettere rappresentano generici sottotermini (cioè sono delle variabili sintattiche:  calcolatore(2));
calcolatore(2));
• sotto ai riquadri sono indicati rimandi ad altri punti de Gli oggetti matematici in cui sono introdotte o commentate e/o sono presenti esempi di impiego ed eventuali avvertenze per l'uso (a cui si può accedere dai riquadri cliccando sulle icone  );
);
• le regole non sono da imparare a memoria: basta un minimo di riflessione o qualche esempio numerico (o geometrico) per individuare i procedimenti che trasformano termini in altri termini equivalenti; per i primi tempi ti può comunque essere utile consultare i riquadri (e le osservazioni che li seguono);
• non c'è un'unica strada da seguire per manipolare un termine: è utile analizzarne la struttura complessiva per scegliere su quale parte incominciare ad operare e in che modo; si possono applicare contemporaneamente più regole (quando si è acquisita una sufficiente padronanza);…
• al posto di alcune regole si può usare una combinazione di altre regole; si vedano le indicazioni in verde presenti nei riquadri (ad es. nel riquadro che descrive la regola (5) è indicato che al suo posto si possono usare la (3) e la (4), delle quali è una conseguenza) e la nota 2;
• se le espressioni manipolate non sono astratte ma modellizzano una particolare situazione, è utile tener conto di questa durante la manipolazione (la cosa è stata già osservata alla voce  formule).
formule).

rimpiazzamento (o sostituzione) di un sottotermine t1 con un sottotermine t2 equivalente |
...t ...
2
... t ... ———>
1 ...(t )...
2 |
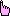 |
(1) |
|
Es.: 2xy + yx → 2xy + xy (t1 è yx, t2 è xy): usando il fatto che yx è equivalente a xy posso sostituire yx con xy ottenendo un termine equivalente a quello di partenza.
 Attenti a: Attenti a:
• Sostituire una espressione che sia effettivamente un sottotermine. Esempi di errore: |
|
x+yz = y+xz | applicando a x+y la regola di riscrittura a+b → b+a:
non si è tenuto conto che x+y non è un sottotermine di x+yz; infatti x+yz, esplicitando tutti i simboli di operazione e delimitando i sottotermini con parentesi, assume la forma: x+(y·z); |
|
|
"semplificando" per 5:
si è agito come se il 1o termine della divisione fosse 10 invece che tutto 10+x. |
• Introdurre, quando è necessario, una coppia di parentesi per delimitare la nuova espressione che rimpiazza la vecchia.
Esempi di errore:
Guadagno = Incasso – Spesa1 + Spesa2 ottenuta da: Guadagno = Incasso – Spese con la sostituzione: Spese = Spesa1 + Spesa2: |
| se non si introduce una coppia di parentesi il secondo termine della sottrazione diventa Spesa1 invece di Spesa1+Spesa2; cioè occorre scrivere: Guadagno = Incasso – (Spesa1 + Spesa2) |
| 3 | x/3 + 7 | = | x + 7 |
| ——— | ——— |
| 2 | 2 |
|
| 3 va moltiplicato per tutto il primo termine della divisione, non solo per 3/x: |
| 3 | x/3 + 7 |
= | 3(x/3 + 7) | = | x + 21 |
| ——— | ———— | ——— |
| 2 | 2 | 2 |
|
 (esempi di (2)-(9) sono alla fine della tabella)
(esempi di (2)-(9) sono alla fine della tabella)
riordino delle addizioni |
caso particolare:
a+b+c ———> c+a+b o b+(a+c) o …
| |
(2) |
|
eliminazione delle negazioni |
--a o -(-a) ———> a
| |
(3) |
|
• portar fuori la negazione da un prodotto
•
eliminazione delle negazioni in un prodotto
(3),(4) → (5) |
a(-b) o (-a)b ———> -ab
(-a)(-b) ———> ab
| |
(4)
(5) |
|
distribuzione (→) e raccoglimento (←) della negazione rispetto all'addizione |
———>
-(a+b+…) -a + -b + …
<———
| |
(6) |
|
differenza in somma (→) e somma in differenza (←)
(6),(7) → (8) |
———>
a-b a + -b
<———
———> a + -b + -c + …
a-(b+c+…)
<——— (o: a - b - c - … )
| |
(7)
(8) |
|
addizione/sottrazione di zero |
———>
a+0 o 0+a o a-0 a
<———
| |
(9) |
|
(2) Esempio di applicazione della riscrittura
a+b+c → b+(c+a): | 12+46·3+8 = 46·3+(8+12)
a b c
|
|
(4),(7←) |
Es.:
53+4·(3-9) = 53+4·(-6) = 53+ -4·6 = 53-4·6 = 53-24 = 29
(4) (7←)
|
|
(3),(4),(5) |
Es.:
-(-3·-2·-1) = -(3·2·-1) = --(3·2·1) = 3·2·1 = 6
(5) (4) (3) [ ] ]
ovvero: -(-3·-2·-1) = ----(3·2·1) = 3·2·1 = 6
3 volte (4) 2 volte (3)
|
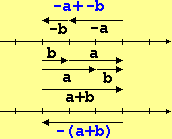
(6),(8) A fianco è raffigurata una spiegazione "fisica" di (6):
eseguire gli spostamenti –a e –b opposti a due spostamenti a e b equivale a eseguire lo spostamento opposto allo spostamento a+b complessivo.
Questa può essere anche una spiegazione di (8):
sottrarre (b+c+…), cioè applicare lo spostamento –(b+c+…), equivale ad applicare gli spostamenti –b, –c, ….
|  |
(2),(7) (7) consente di interpretare una sequenza di addizioni e sottrazioni come una sequenza di sole addizioni, così da poterla riordinare; due esempi legati all'uso della CT:  , ,  ; un altro es.: ; un altro es.: |
| | (2) (7←)
1 1 1 1 1
4- — +8 = 4+ - — +8 = 4+8+ - — = 12+ - — = 11- —
7 7 7 7 7
(7→) (1)
|
|
(7←),(8←) nel trasformare 3–x+y–z in 3+y–(x+z) posso usare solo (7) o anche (8): |
| |
(7) 3–x+y–z = 3+y+(–x+–z) = 3+y+–(x+z) = 3+y–(x+z)
/ \
trasformo le differenze in raccolgo la negazione
somme e riordino la somma
(8) 3–x+y–z = 3+y–x–z = 3+y–(x+z)
/ \
trasf. diff. in somme, riordino trasf. differenze
somma e trasf. somme in differenze in somma con (8)
|
 (esempi di (10)-(19) sono alla fine della tabella)
(esempi di (10)-(19) sono alla fine della tabella)
riordino delle moltiplicazioni |
caso particolare:
abc ———> cab o b(ac) o …
| |
(10) |
|
eliminazione dei reciproci |
-1
1 -1
—— o (a ) o … ———> a
1
—
a
-1
a b
(——) ———> ——
b a
|
 |
(11)
(12) |
|
distribuzione (→) e raccoglimento (←) del reciproco rispetto alla moltiplicaz. |
1 ———> 1 1
——— — —
ab <——— a b
| |
(13) |
|
rapporto in prodotto (→) e prodotto in rapporto (←) |
a ———> 1 -1
—— a — o ab
b <——— b
| |
(14) |
|
eliminare fattori comuni ai 2 termini di una divisione (→) e moltiplicare/dividere i 2 termini per uno stesso termine (←) |
ab ba a/b ———> a
—— o —— o ——— ——
cd bc c/b <——— c
|
 |
(15) |
|
altre trasformazioni di divisioni
(14) → (16)
(12),(14) → (17) |
a
—
b ———> a
—— o a/b/c ———
c <——— bc
a ac a c
—— o a/(b/c) ———> —— o — c o a —
b b b b
—
c
|
 |
(16)
(17) |
|
• moltiplicazione per zero
• moltiplicazione per uno |
———>
a·0 o 0·a o 0/a 0
<———
———>
a·1 o 1·a o a/1 a
<———
|  |
(18)
(19) |
|
|
(11) |  |
(12) un  esempio; un altro esempio; un altro  ; un nuovo esempio: ; un nuovo esempio: |
| |
3
—————— →
133+88 | 133  88 88   3 3  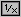
|
|
(10),(13),(14) (13) e (14) consentono di interpretare una sequenza di moltiplicazioni e divisioni come una sequenza di sole moltiplicazioni, così da poterla riordinare: |
4 6 1 -2 1 -2 -2 -2
—·2·———·9 = 4·—·2·6·10 ·9 = 4·2·6·(9·—)·10 = 48·1·10 = 48·10
9 2 9 9
10 (8)
(14→)
x 1 1 1 1 1 1 x·y
——·z·y = x·——·z·y = x·(—·—)·z·y = x·z·(—·y)·— = x·z·1·— = ———
2y 2y 2 y y 2 2 2
(14→) (13→) (8)
|
altro es. di (14→):
3
——————
133+88
| → 133  88 88  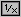 3 3  3 3  |
|
 Attenti: l'operazione di passaggio al reciproco si può distribuire rispetto alla moltiplicazione - vedi (13) - non rispetto
all'addizione: Attenti: l'operazione di passaggio al reciproco si può distribuire rispetto alla moltiplicazione - vedi (13) - non rispetto
all'addizione: |
| 1 | non equivale a | 1 | + | 1 |
| —— | — | — |
| x + y | x | y |
|
(15)  esempi; un altro es.: come trasformare 2000/150 in un termine più semplice da calcolare: esempi; un altro es.: come trasformare 2000/150 in un termine più semplice da calcolare: |
2000 200 400 40
———— = ——— = ——— = ——
150 15 30 3
(15→) (15←) (15→)
|
|
(16←) es.: calcolo mentale di 155/6: |
155/6 = 155/3/2 = (circa) 50/2 = 25
|
| 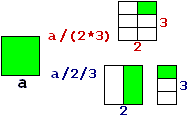 |
|
|
(16→) es.: calcolo di 78/5/2: |
78/5/2 = 78/10 = 7.8
|
|
|
(17) es.: calcolo di 100/(2/3): |
100 100
——— = ———·3 = 50·3 = 150
2/3 2
|
 Attenti: in alcuni casi, applicando (11), (15) o (17), si può ottenere un termine che non è definito mentre lo era il termine di partenza: Attenti: in alcuni casi, applicando (11), (15) o (17), si può ottenere un termine che non è definito mentre lo era il termine di partenza: |
2·x·x 2·x
————— —> ———
3·x 3 |
|
il 1° termine non è definito per x=0, mentre il 2° è sempre definito |
5 5
——————— —> —(x-2)
3/(x-2) 3 |
|
il 1° termine non è definito per x=2, mentre il 2° è sempre definito |
|
|
il 1° termine non è definito per x=0, mentre il 2° è sempre definito |
 Attenti: applicando (18) si può ottenere un termine che non è definito mentre lo era il termine di partenza, o viceversa. Ad esempio la seguente trasformazione, ottenuta applicando (18→), ha dato luogo al termine x2 che è definito per qualunque valore si assegni ad x, mentre il termine di partenza non era definito per x negativo: Attenti: applicando (18) si può ottenere un termine che non è definito mentre lo era il termine di partenza, o viceversa. Ad esempio la seguente trasformazione, ottenuta applicando (18→), ha dato luogo al termine x2 che è definito per qualunque valore si assegni ad x, mentre il termine di partenza non era definito per x negativo:
√x · (4 – 5 + 1) + x2 → √x · 0 + x2 → 0 + x2 → x2 |
|
(19←) è usata in varie attività di "semplificazione": |
x 1·x 1
——— = ——— = — (kx+x) = (kx+1x) = (k+1)x
2·x 2·x 2
(19) (15) (19) (20) |

distribuzione (→) della moltiplicazione rispetto all'addizione
e raccoglimenti (←) |
———>
a(b+c+ …) ab + ac + …
<———
———>
(b+c+ …)a ba + ca + …
<———
| |
(20) |
|
| • |
trasformando |
12 4
—— - —
7 7 |
in |
8
—
7 |
(somma di frazioni) implicitamente raccolgo 1/7: |
12 4 1 1 1 1 8
—— - — = 12 — + - 4 — = (12 + - 4) — = 8 — = —
7 7 7 7 7 7 7
(7,14) (20)
|
| • |
nel trasformare 99·7 in 700–7 implicitamente distribuisco 7: |
99·7 = (100 - 1)·7 = (100 + -1)·7 = 100·7 + -1·7 = 700-7 = 693
(7) (20)
|
| • |
per calcolare 10012 posso fare: |
2
(1000+1)(1000+1) = 1000(1000+1)+1(1000+1) = 1000 +1000+1000+1 = 1002001
(20) (20)
|
o usare direttamente la riscrittura (a+b)2 ——> a2+2ab+b2 (20*)
ottenibile in modo analogo: |
(a+b)(a+b) = a(a+b)+b(a+b) = a·a+a·b+b·a+b·b = a·a+2·a·b+b·b
(20) (20) (10)
|
| • |
per calcolare 9992 posso usare (20*) pensando (a–c)2 come (a+(-c))2 : |
2 2 2
(1000–1) = 1000 + 2·1000·(–1) + 1 = 1000 000 – 2000 + 1 = 998 001
|
 Attenti: spesso per effettuare dei raccoglimenti occorre prima
usare la proprietà (19←) dell'uno: Attenti: spesso per effettuare dei raccoglimenti occorre prima
usare la proprietà (19←) dell'uno:
a + b a
→ 1·a + b a
→ (1 + b) a
27·0.8 − 27
→ 27·0.8 − 27·1
→ 27·(0.8−1)
→ −27·0.2 = −5.4
|

|
(21→) es.: calcolo "a mano" di 52+(5·3)2: |
2 2 2 2 2 2 2
5 +(5·3) = 5 +5 ·3 = 5 ·(1+3 ) = 25·(1+9) = 25·10 = 250
(21) (20)
|
|
(22←) es.: √8·√2 = √(8·2) = √16 = 4 |
|
(22→) es.: √0.04 = √(4·(1/100)) = √4·√(1/100) = 2·(1/10) = 0.2 |
 Attenti: in alcuni casi, distribuendo, si può ottenere un termine che non è definito mentre lo era il termine di partenza: Attenti: in alcuni casi, distribuendo, si può ottenere un termine che non è definito mentre lo era il termine di partenza:
(xy)1/2, cioè √(xy), se x e y sono negativi è definito in quanto xy diventa positivo, mentre x1/2·y1/2, cioè √x·√y, non è definito: per x = –2, y = –8 √(xy) = √16 = 4 mentre √x·√y = √–2·√–8 è indefinito.
E viceversa:
passando da √x·√y a √(xy) il dominio viene allargato. |
 Attenti: potenze e radici si possono distribuire rispetto alla moltiplicazione, non rispetto
all'addizione (vedi anche più avanti Attenti: potenze e radici si possono distribuire rispetto alla moltiplicazione, non rispetto
all'addizione (vedi anche più avanti  ): ):
√(x + y) non equivale a √x + √y e (x + y)3 non equivale a x3+ y3. |

|
|
(23),(24) Con queste espressioni («raggruppare i termini …») si
intende l'applicazione di riordinamenti e, nel caso di (23), di
raccoglimenti a fattor comune o, nel caso di (24), di proprietà
delle potenze,
al fine di ottenere una somma o un prodotto equivalente a quello di
partenza ma costituito da un minor numero di addizioni (e
sottrazioni) o da un minor numero di moltiplicazioni (e divisioni): |
Esempio di (23): 2·(–4 + 3√5 + 7x – √5 – x + 1) = 2·(6x + 2√5 – 3)
si tratta di un riordino di una sequenza di addizioni e sottrazioni:
2·(–4 + 3√5 + 7x – √5 – x + 1) →
(7x – x) + (3√5 – √5) + (–4 + 1)
seguito da raccoglimenti a fattor comune:
7x – x → (7 – 1)x, 3√5 – √5 → (3 – 1)√5
e dall'esecuzione di calcoli numerici:
7 – 1 → 6, 3 – 1 → 2, –4 + 1 → –3
|
|
Esempio di (24): |
6 5 x+y 3 7
2·(x+y) ·10 ·——— = 2·10 ·(x+y)
2
10
|
| si tratta di un riordino di una sequenza di moltiplicazioni e divisioni: |
6 5 x+y 5 -2 6
2·(x+y) ·10 ·——— —> 2·(10 ·10 )·((x+y) ·(x+y))
2
10
|
| seguito dall'applicazione della riscrittura abac → ab+c: |
5 -2 6 5-2 6+1
2·(10 ·10 )·((x+y) ·(x+y)) —> 2·10 ·(x+y)
|
| e dalla esecuzione di calcoli numerici: |
5-2 —> 3, 6+1 —> 7
|
(25),(26) Queste trasformazioni, scritte come: a + –a → 0 e a · a–1 → 1, caratterizzano l'opposto/il reciproco di un numero a come quel numero che addizionato/moltiplicato per a dà come risultato zero/uno, cioè  l'elemento neutro rispetto alla addizione/moltiplicazione. l'elemento neutro rispetto alla addizione/moltiplicazione. |
 Attenti: l'uso di Attenti: l'uso di  (25) e (26) – diretto o nell'ambito di attività di ragguppamento: (23) e (24) – così come il ricorso a proprietà delle potenze, può dar luogo a un termine che è definito anche in casi in cui non lo era il termine di partenza: (25) e (26) – diretto o nell'ambito di attività di ragguppamento: (23) e (24) – così come il ricorso a proprietà delle potenze, può dar luogo a un termine che è definito anche in casi in cui non lo era il termine di partenza:
• √x – √x + 2x → 2x usando (25) e (9): un termine definito solo per x≥0 diventa un termine definito per ogni valore di x
• (u/u – 2)u → –u usando (26) e (19): un termine definito solo per u diverso da 0 diventa un termine definito per ogni valore di u
• b–2·b3 → b usando le proprietà delle potenze: un termine definito solo per b diverso da 0 diventa un termine definito per ogni valore di b
|

|
In questo modo vengono spesso chiamati i raccoglimenti a fattor comune, cioè (20, ←), e le distribuzioni di potenze e radici rispetto alla moltiplicazione, cioè (21, →) e (22, →); casi particolari sono discussi più avanti:  , ,  [con fattore si intende un termine di una moltiplicazione] [con fattore si intende un termine di una moltiplicazione] |
portar dentro
portar fuori |
|
Con "portar fuori" (da una potenza, da una radice, da una somma,…) in genere si indicano delle fattorizzazioni (vedi sopra). Ad es. portar fuori z da √(xyz) dà luogo a √z·√(xy), portar fuori z da 2kz+kxz dà luogo a (2k+kx)z.
Con "portar dentro" si intendono le trasformazioni opposte: portar z dentro alla somma trasforma (2k+kx)z in 2kz+kxz, portar z dentro alla potenza trasforma z4(xy)2 in (z2xy)2.
|
|
In questo modo vengono spesso chiamate le trasformazioni che si ottengono applicando raggruppamenti di somme e di prodotti, cioè (23) e (24), e l'eliminazione di fattori comuni tra i due termini di una divisione, cioè (15, →), la cosiddetta "semplificazione delle frazioni", oltre all'effettuazione di eventuali calcoli numerici (2+3 = 5, …) o basati sulle proprietà di 0 e di 1, cioè (9), (18) e (19), o delle potenze. |
|
In questo modo vengono spesso chiamate le trasformazioni che si ottengono applicando distribuzioni della moltiplicazione rispetto alla addizione, cioè (20, →) e (6, →) (con cui si passa da un termine con parentesi a un termine senza parentesi), e trasformazioni di divisioni come (16, →) e (17) (con cui si passa da termini a più "piani" a termini a soli due "piani"), oltre all'effettuazione di eventuali calcoli numerici (2+3 = 5, …) o basati sulle proprietà di 0 e di 1, cioè (9), (18) e (19), o delle potenze. |
| Un agettivo spesso usato è irriducibile, sia per indicare una frazione non ulteriormente semplificabile, sia per indicare un termine che, in un particolare
ambito (da precisare caso per caso), non è ulteriormente fattorizzabile. |
 Nota 2. Di molte delle regole che abbiamo descritto si potrebbe fare a meno usando al loro posto la combinazione di altre regole. Qualche esempio è indicato nelle parti in verde dei riquadri. Ad esempio l'osservazione "(14) →(16)" significa che al posto dell'uso diretto di "a/b/c → a/(b·c)" si può fare "a/b/c → a·(1/b)·(1/c) → a·((1/b)·(1/c)) → a·(1/(b·c) → a/(b·c)". Vediamo qualche altro esempio. Nota 2. Di molte delle regole che abbiamo descritto si potrebbe fare a meno usando al loro posto la combinazione di altre regole. Qualche esempio è indicato nelle parti in verde dei riquadri. Ad esempio l'osservazione "(14) →(16)" significa che al posto dell'uso diretto di "a/b/c → a/(b·c)" si può fare "a/b/c → a·(1/b)·(1/c) → a·((1/b)·(1/c)) → a·(1/(b·c) → a/(b·c)". Vediamo qualche altro esempio.
• Al posto della (15 →) si potrebbero usare (13 →), (14 →), (10) e (13 ←):
ab 1 1 1 1 1 1 a
—— = ab —— = ab(— —) = a— (b—) = a— = —
cb cb c b c b c c
• Al posto della (6 →) si potrebbe usare (20 →) -(a+b) = (-1)·(a+b) = (-1)·a+(-1)·(b) = -a + -b
| | |
-x=(-1)x distribuisco -1 (-1)x=-x
Nota 3. Negli esempi sotto ai riquadri abbiamo effettuato le manipolazioni dei termini esplicitando molti passaggi intermedi. Man mano che ci si impratichisce si possono saltare gran parte di questi passaggi. Occorre tuttavia non cercare di abbreviare i procedimenti a tutti i costi: si corre il rischio di commettere errori, come quelli segnalati nelle "avvertenze" richiamate nei riquadri e nei commenti presenti nelle righe sottostanti.
 Abbiamo già richiamato - vedi Abbiamo già richiamato - vedi  le avvertenze all'uso delle sostituzioni, regola (1) - alcuni errori che è facile commettere se non si analizza attentamente la struttura del termine che si vuole trasformare. le avvertenze all'uso delle sostituzioni, regola (1) - alcuni errori che è facile commettere se non si analizza attentamente la struttura del termine che si vuole trasformare.
Si possono fare errori anche riferendosi a espressioni verbali come "cancello", "porto fuori", "semplifico", … senza tener conto delle diversità di significato rispetto al linguaggio comune; ad es. in: |
* *
(3x+3)(x-1-x+1)+4 → (3x+3)+4 → 3x+3+4
* * |
| si è "cancellato" facendo x–x → "niente" e 1–1 → "niente",
mentre si sarebbe dovuto fare x–x → 0 e 1–1 → 0 (ottenendo:
(3x+3)·0+4 = 0+4 = 4), e in: |
* *
y+by
———— → b/a
ay
* |
| si sono "cancellate" le y di sopra e la y di sotto semplificando per y, mentre la semplificazione dovrebbe avvenire dividendo il termine di sopra e quello di sotto per y e poi facendo y/y → 1 (in pratica per il primo y di sopra si è invece fatto y/y → "niente"), in modo da ottenere (1+b·1)/(a·1) = (1+b)/a; ovvero facendo (in forma scritta o mentalmente) la trasformazione y+by → 1·y+b·y → (1+b)y e poi "eliminando" il fattore y comune al secondo termine della divisione, ay. |
Vediamo qualche altro errore abbastanza comune, in cui si inventano regole in analogia con regole effettivamente impiegabili:
• posso fare
√(4·9) = √4·√9
non posso fare
√(4+9) = √4+√9 | | la radice è distribuibile rispetto alla moltiplicazione, non rispetto alla addizione. |
• posso fare
5(x+y) = 5x+5y e -(a+b) = -a-b
non posso fare | | posso distribuire i fattori moltiplicativi e le negazioni rispetto alla addizione, non rispetto alla divisione |
2 2y
———·y = ———————
x+y (x+y)·y
| | né |
| -(a·b) = (-a)·(-b) |
• posso fare
(5·2)3 = 53·23;
non posso fare
45·2 = 45·42 | | posso distribuire l'esponente rispetto alla moltiplicazione, non posso distribuire la base. |
 Nota 4. Spesso invece di termini algebricamente equivalenti si parla più semplicemente di termini equivalenti. Occorre però aggiungere la specificazione "algebricamente" quando si vuole fare una distinzione da altri tipi di equivalenza: Nota 4. Spesso invece di termini algebricamente equivalenti si parla più semplicemente di termini equivalenti. Occorre però aggiungere la specificazione "algebricamente" quando si vuole fare una distinzione da altri tipi di equivalenza:
due termini possono essere algebricamente equivalenti ma non essere equivalenti dal punto di vista della precisione del calcolo (se i calcoli vengono eseguiti con un mezzo di calcolo che opera con una quantità fissata di cifre i due termini possono dar luogo a due risultati differenti) o dal punto di vista del tempo di calcolo.
Ad esempio x+y–z (x  y y  z z  ) e –z+x+y (z ) e –z+x+y (z   x x  y y  ), calcolati con una CT che arrotonda a 10 cifre, nel caso in cui x = z = 12345678 e y = 0.12345678 risulterebbero avere rispettivamente i valori 0.12 e 0.12345678 (nel primo caso, infatti, 12345678+0.12345678 = 12345678.12345678 verrebbe arrotondato a 12345678.12). Per la CT i due termini non sono quindi "numericamente" equivalenti. Non sono equivalenti neanche temporalmente: nel secondo caso devo battere un tasto in più. ), calcolati con una CT che arrotonda a 10 cifre, nel caso in cui x = z = 12345678 e y = 0.12345678 risulterebbero avere rispettivamente i valori 0.12 e 0.12345678 (nel primo caso, infatti, 12345678+0.12345678 = 12345678.12345678 verrebbe arrotondato a 12345678.12). Per la CT i due termini non sono quindi "numericamente" equivalenti. Non sono equivalenti neanche temporalmente: nel secondo caso devo battere un tasto in più.
Esercizio (e soluzione)
Esercizi: 
 altri collegamenti [nuova pagina] altri collegamenti [nuova pagina]

|
|
 Due termini vengono detti algebricamente equivalenti quando assumono gli stessi valori, cioè: comunque sostituisco valori alle eventuali variabili che compaiono in essi, ottengo due termini che sono entrambi definiti o entrambi indefiniti e, nel primo caso, hanno lo stesso valore.
Due termini vengono detti algebricamente equivalenti quando assumono gli stessi valori, cioè: comunque sostituisco valori alle eventuali variabili che compaiono in essi, ottengo due termini che sono entrambi definiti o entrambi indefiniti e, nel primo caso, hanno lo stesso valore.
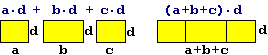


 sul visore ricompare il numero di partenza può suggerire la regola
sul visore ricompare il numero di partenza può suggerire la regola  );
);


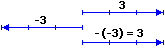


 88
88 
 3
3  3
3 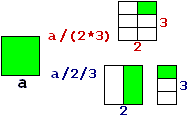

 z
z